Похожие презентации:
Численное решение обыкновенных дифференциальных уравнений
1. Численное решение обыкновенных дифференциальных уравнений
2. Обыкновенное дифференциальное уравнение
• это математическое уравнение, котороесодержит неизвестную функцию одной
переменной и её производные. Неизвестная функция
обычно представлена переменной у, которая зависит от x,
поэтому x часто называют независимой переменной
уравнения.
3. Общая формула
• F(x, y, y', y'', ...) = 0,• где x — независимая переменная,
• y — зависимая переменная,
• y', y'' и т. д. обозначают производные первого, второго и
более высокого порядка от y по отношению к x
соответственно.
4. Задача Коши для одного обыкновенного дифференциального уравнения.
• Рассмотрим задачу Коши относительно производной:5. Задача Коши для одного обыкновенного дифференциального уравнения.
6. Многие ОДУ не имеют аналитического решения, поэтому используются численные методы.
• Метод Эйлера• Метод Рунге-Кутты
• Метод Адамса-Бэшфорта
• Метод Адамса-Моултона
7. Метод Эйлера для численного решения обыкновенных дифференциальных уравнений
• это простейший численный метод решения обыкновенныхдифференциальных уравнений (ОДУ) первого порядка.
• Он основан на идее приближённого вычисления значений
искомой функции на дискретной сетке с помощью
линейной аппроксимации. Метод широко используется
благодаря своей простоте и наглядности, хотя обладает
невысокой точностью.
8. Постановка задачи
• Рассмотрим задачу Коши для ОДУ первого порядка:где f(x,y) — заданная функция, y(x0)=y0 — начальное условие.
Требуется найти приближённое значение функции y(x) в
точке xn=x0+nh, где h — шаг интегрирования.
9. Алгоритм метода
10. Пример 1
• Найти решение ОДУ c заданными параметрами• Пусть уравнение имеет вид f(x, y) или системе вида y′ = f(x,
y). Начальное значение y(a) = y0 на левом краю отрезка [a,
b]. Шаг h задан. Число шагов n вычисляется примерно как
(b − a)/h, целое приближение.
11. Решение
• Шаг 1. Приведем уравнение в стандартную форму12. Шаг 2. Параметры метода
13. Шаг 3. Применение формулы Эйлера
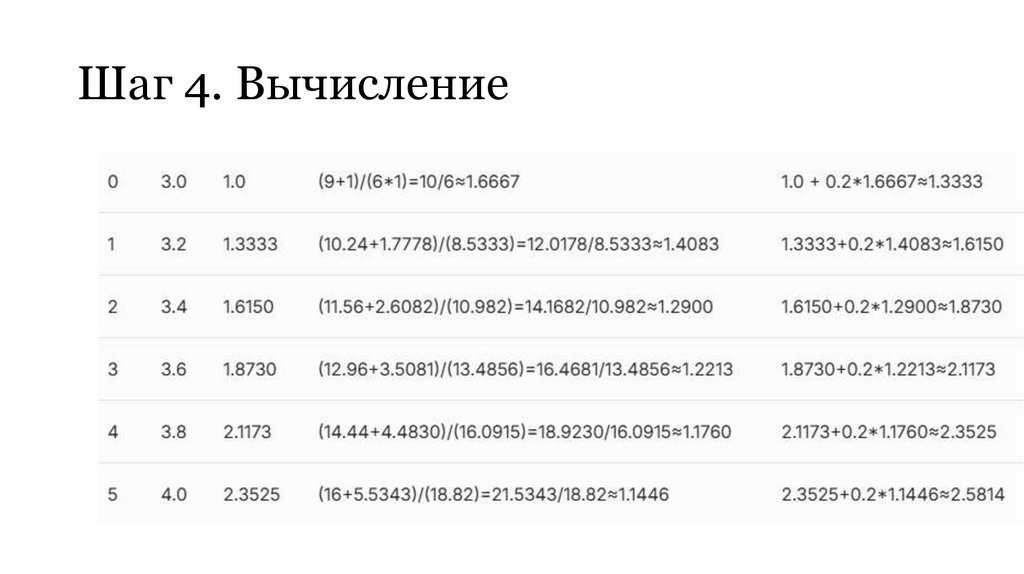
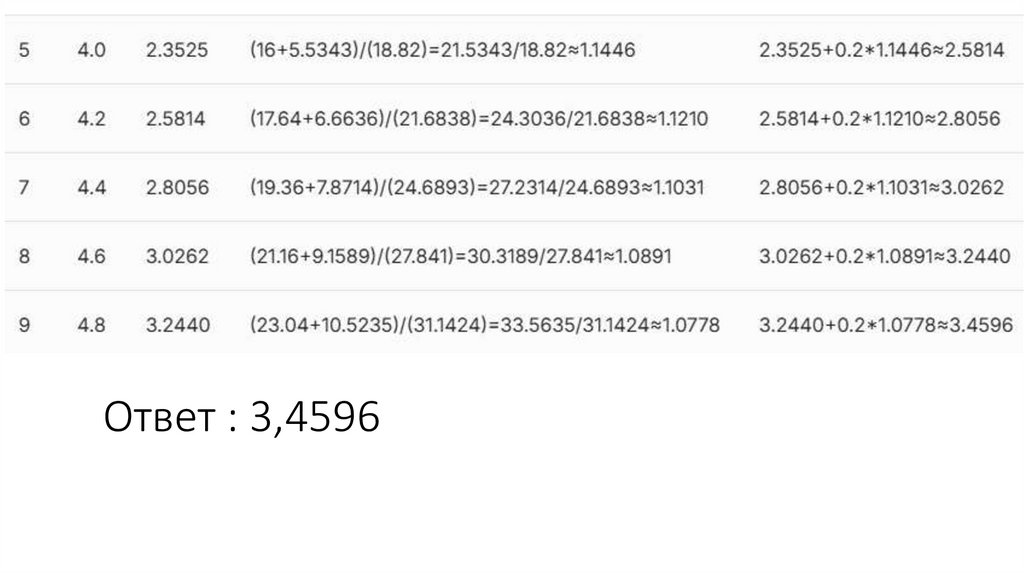
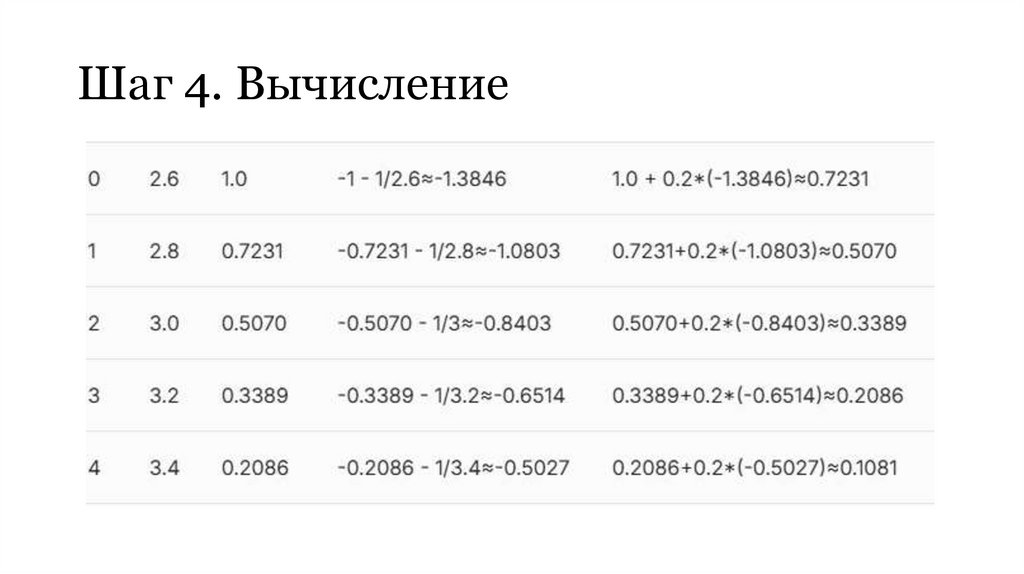
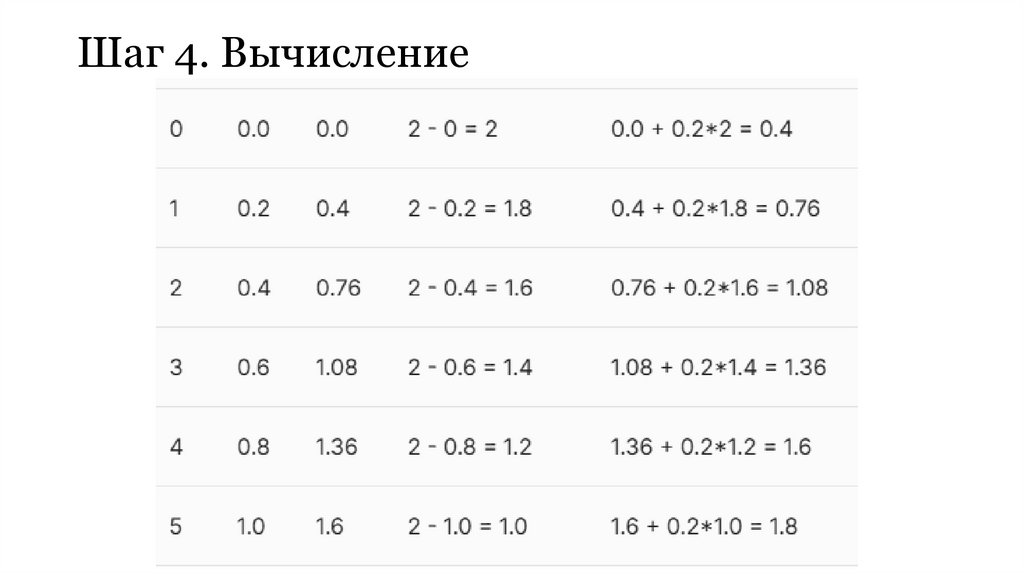
14. Шаг 4. Вычисление
15. Ответ : 3,4596
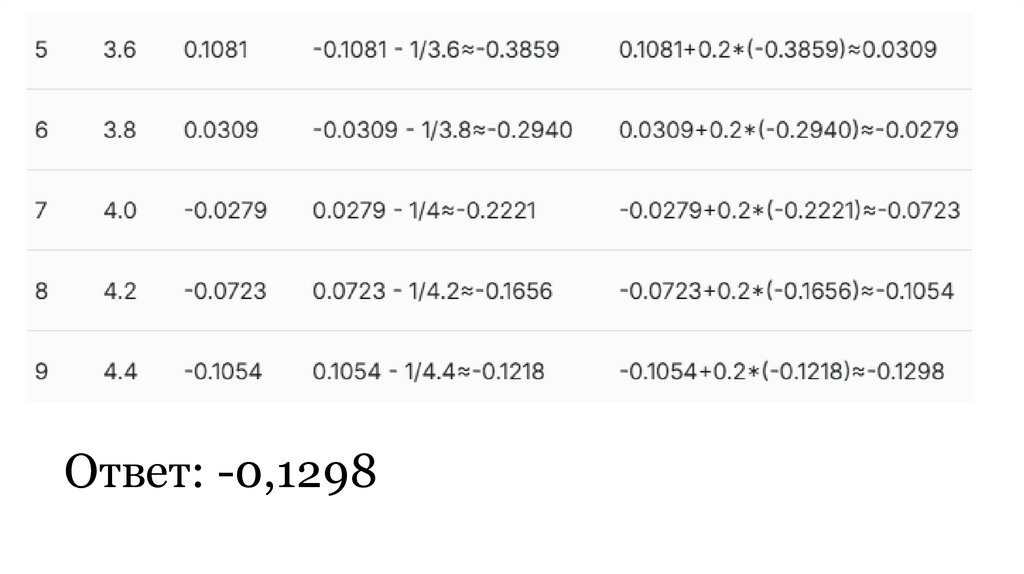
16. Пример 2.
17. Шаг 1. Приведение в стандартную форму
• Приведение уравнения в стандартную формуне требуется





































 Математика
Математика








