Похожие презентации:
Численные методы решения обыкновенных дифференциальных уравнений
1. Численные методы решения обыкновенных дифференциальных уравнений
2. Постановка и решение задачи Коши
Решением дифференциальногоуравнения (ДУ) I порядка
y’ = f (x,y) ,
разрешенного относительно
производной, называется функция
y = (x) ,
которая при подстановке в уравнение
обращает его в тождество
3. Постановка и решение задачи Коши
Решением дифференциальногоуравнения (ДУ) I порядка
y’ = f (x,y) ,
разрешенного относительно
производной, называется функция
y = (x) ,
которая при подстановке в уравнение
обращает его в тождество
’(x) f (x, (x)) .
4. Постановка и решение задачи Коши
Задача Коши для одногодифференциального уравнения
первого порядка разрешенного
относительно производной
y’= f(x,y)
y(x0)= y0
состоит в нахождении частного
решения ДУ, удовлетворяющего
начальному условию y(x0)= y0.
5. Постановка и решение задачи Коши
Геометрический смысл задачи Коши:найти такую интегральную кривую
(график решения), которая
проходит через заданную начальную
точку M(x0, y0).
6. Постановка и решение задачи Коши
Геометрический смысл задачи Коши:найти такую интегральную кривую
(график решения), которая
проходит через заданную начальную
точку M(x0, y0).
7. Постановка и решение задачи Коши
Возможны 2 пути решения задачи Коши:1. Аналитический
2. Численный
8. Постановка и решение задачи Коши
Решить задачу Коши численно —значит для заданной
последовательности значений
аргумента (узлов ) x0, x1, … xn , и
числа y0 (значение искомой функции в
начальном узле x0 ), не находя самогo
решения y = (x) , приближенно
вычислить значения
y1, y2, ….yn
этого решения в остальных узлах.
9. Постановка и решение задачи Коши
Численное решение задачи Кошипозволяет вместо отыскания точного
решения y = (x) в виде формулы
получить таблицу значений
xi
x0
x1
x2
(xi) (x0) y1
yn
…
xn
yn
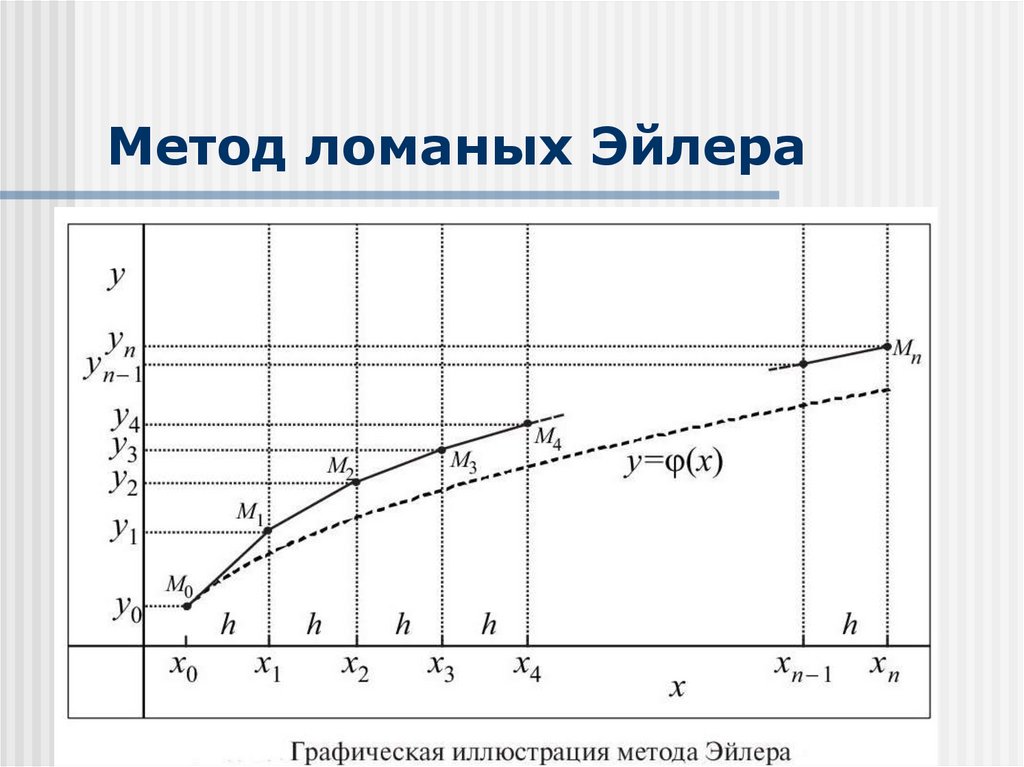
10. Метод ломаных Эйлера
основан на кусочной замене искомойфункции полиномом первой степени,
т. е. на линейной интерполяции.
11. Метод ломаных Эйлера
Рассмотрим систему равноотстоящихузлов
x 0 , x 1 , … x n,
где xk= x0 +kh, k=1, 2, 3,….
12. Метод ломаных Эйлера
Будем искать решение в видеyk+1= yk +h f (xk ,yk) .
13. Метод ломаных Эйлера
14. Метод Эйлера : выводы
Метод Эйлера — представительодношаговых приближенных методов,
в которых решение в (k +1)-м узле
получается на основе решения только
в одном предыдущем k-м узле. Тем
самым информация о более ранних
уже вычисленных значениях
игнорируется
15. Метод Эйлера : выводы
Как и в любом одношаговом методе,начиная со второго шага исходное
значение yk в формуле
yk+1= yk +h f (xk ,yk)
самo является приближенным, т. е.
погрешность на каждом последующем
шаге систематически возрастает.
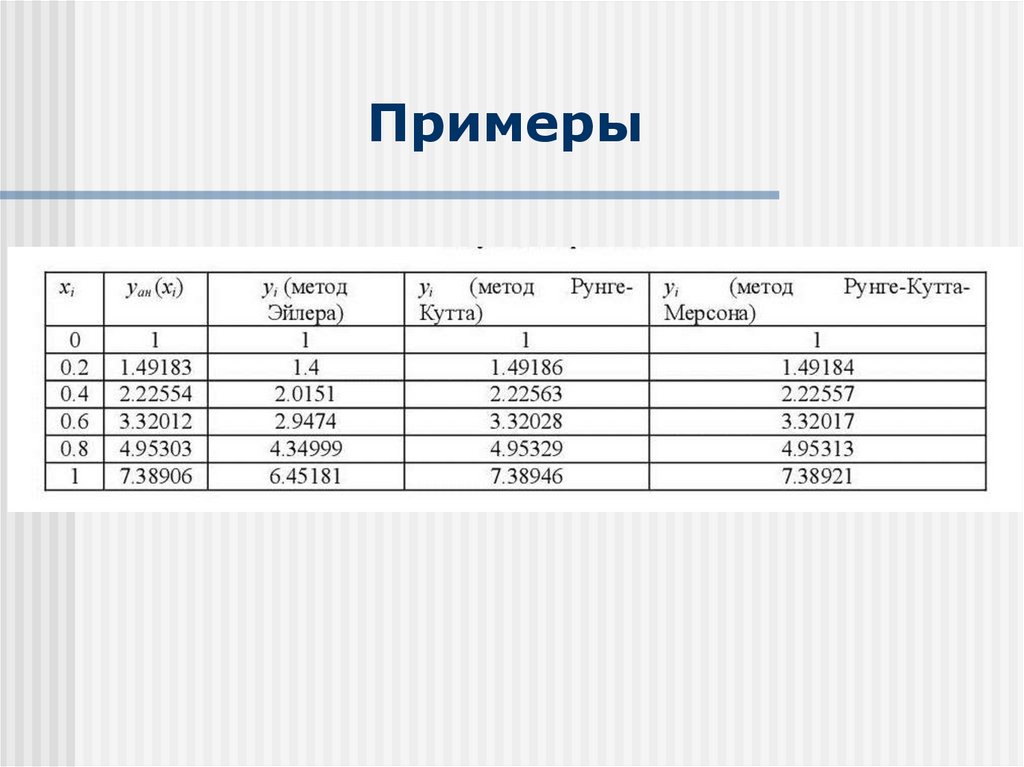
16. Примеры
Решить задачу Кошиy’=-y
y(0)=1
17. Примеры
Точное решениеy=e-x
18. Примеры
Теперь применим приближенныйметод Эйлера
f (x, y) = -y, x0 =0 ; y0 =1
yk+1= yk +h f (xk ,yk), k=1, 2, 3, 4, 5
Пусть h=0.2
yk+1= 0.8yk
19. Метод Эйлера : выводы
Погрешность метода О(h)Уменьшение h повышает точность
вычислений, но резко увеличивает их
объем.
В целом метод ломаных Эйлера
применим только для грубой прикидки
20. Модифицированный метод Эйлера
21. Модифицированный метод Эйлера
22. Модифицированный метод Эйлера – Коши
23. Модифицированные методы Эйлера
Точность методов O(h2)24. Примеры
Теперь применим приближенныйметод Эйлера
f (x, y) = -y, x0 =0 ; y0 =1
yk+1= yk +h f (xk ,yk), k=1, 2, 3, 4, 5
Пусть h=0.2
yk+1= 0.8yk
25. Методы Рунге-Кутты
Идея, предложенная Рунге (1856–1927) и Куттой (1867–1944),
заключается в том, чтобы при
численном решении задачи Коши
использовать значение функции
f(x,y), вычисляя ее на каждом
шаге ее значения в нескольких
точках
26. Методы Рунге-Кутты
Идея, предложенная Рунге (1856–1927) и Куттой (1867–1944),
заключается в том, чтобы при
численном решении задачи Коши
использовать значение функции
f(x,y), вычисляя ее на каждом
шаге ее значения в нескольких
точках
27. Метод Рунге-Кутты IV порядка
28. Примеры
Решить задачу Кошиy’=y(1-x)
y(0)=1
29. Примеры
Точное решение30. Примеры
Правая часть уравненияf(x,y)=y(1-x)
x0=0, y0=1
31. Примеры
32. Примеры
Рассмотрим уравнениеy’+y=3e2x
на интервале x [0, 1]
Точное решение уравнения
y(x)=e2x
33. Примеры
34. Конечно-разностные методы
Рассмотренные выше методы требуютмногократного вычисления значений
правой части уравнения.
Можно воспользоваться функции
конечноразностной аппроксимацией.
35. Конечно-разностные методы
Пусть рассматривается задачаy’= f(x,y)
y(x0)= y0
36. Конечно-разностные методы
Решение:1. Найдем решение уравнения в
первых p точках одним их
описанных методом
2. Для следующих точек решение
будем искать в виде
37. Конечно-разностные методы
3. Заменим подинтегральную функциюинтерполяционным многочленом
4. Вычислим значения функции в
оставшихся точках
38. Конечно-разностные методы
Возьмем в качествеинтерполяционного многочлена
формулу Ньютона
интерполирования вперед
39. Конечно-разностные методы
Получим экстраполяционнуюформулу Адамса
40. Конечно-разностные методы
Экстраполяционная формула Адамсапри n=3:
41. Конечно-разностные методы
При использовании формулыНьютона интерполирования назад,
получаем интерполяционную
формулу Адамса (при p=3)
42. Разностные методы для краевых задач
При использовании формулыНьютона интерполирования назад,
получаем интерполяционную
формулу Адамса (при p=3)








































 Математика
Математика








