Численные методы обыкновенных дифференциальных уравнений

1.

Численные методы обыкновенных
дифференциальных уравнений

2.

Постановка задачи
Уравнения, содержащие производную функции одной
переменной, возникают во многих областях физики,
химии, биологии, экономики и пр.
Вообще говоря, любая ситуация, где рассматривается
степень изменения одной переменной по
отношению к другой, описывается
дифференциальным уравнением. Это задачи,
связанные с силой и движением, передачей тепла,
диффузией, распространением колебаний и др.

3.

Пример.
Степень радиоактивности пропорциональна
количеству остающегося радиоактивного
вещества. Соответствующее дифференциальное
уравнение записывается в виде:
y Ry
'

4.

Пример
Рассмотрим решение ОДУ
y y
'
или dy y (1),
dx
в котором изменение y по отношению к x
равно y .

5.

y y
'
Это уравнение можно решить аналитически
(интегрированием):
dy
y;
dx
dy
x c
x
c
x
dx
;ln
y
x
c
;
y
e
e
e
ae
y
Т.о., уравнение (1) имеет аналитическое
решение y ae (2), где a - константа.
x

6.

На рисунке
изображено
семейство
кривых, каждая
из которых –
решение ОДУ
(1).
dy
y
dx

7.

Чтобы решение исходного уравнения (1) было
единственным, необходимо задать значение y
для некоторого x . Тогда можно определить
постоянную a в уравнении (2).
Пусть y(x0)=y0 – задано начальное условие. В
рассмотренном примере: x0=0; y0=1, тогда при
этом из всего семейства кривых только одна
будет удовлетворять двум условиям
одновременно:
dy
y
dx
y (0) 1
a 1

8.

Задача Коши
Задача, включающая дифференциальное
уравнение и начальные условия,
называется задачей Коши для
дифференциального уравнения.
y f ( x, y) (3)
y( x0 ) y 0 (4)
В общем случае в ДУ могут входить
производные более высоких порядков.

9.

В приведенном примере решение задачи
Коши найдено прямым интегрированием –
аналитически, через элементарные
функции. Между тем весьма часто при
решении практических задач этот метод
оказывается либо беспомощным, либо их
решение требует недопустимых затрат
усилий и времени.
По этой причине для решения задач
практики созданы методы приближённого
решения ДУ.

10.

В зависимости от формы представления
решения, методы решения ОДУ
подразделяют на три основных группы:
Аналитические методы – приближённое
решение получается в виде
аналитического выражения.
Графические методы – приближённое
решение получается в виде графика
функции.
Численные методы – искомая функция
получается в виде таблицы.

11.

Классы уравнений, для которых применимы
точные методы, сравнительно узки и
охватывают малую часть возникающих на
практике задач.
Приближёнными называются методы, в
которых решение получается как предел
некоторой последовательности функций,
причём каждый член этой
последовательности выражается через
элементарные функции (например,
решением методом Гаусса – разложение
функции в степенной ряд).

12.

Метод Эйлера (метод ломаных)
Выделим отрезок [x0,X], на котором будем
строить приближённое значение задачи
(3)-(4), и разделим его на n равных частей,
так что
где h -шаг изменения
X x0
h, X x0 nh аргумента.
n

13.

Допустим, что внутри промежутка
от x0 до x0+h функция y’ сохраняет
постоянное значение y’= f(x0,y0),
тогда y1-y0 hf(x0,y0), где y1 – значение
искомой функции в точке x1.
Отсюда
y1 y0+ hf(x0,y0).
y2 y1+ hf(x1,y1)
(5)
………………..
yn yn-1+ hf(xn-1,yn-1)

14.

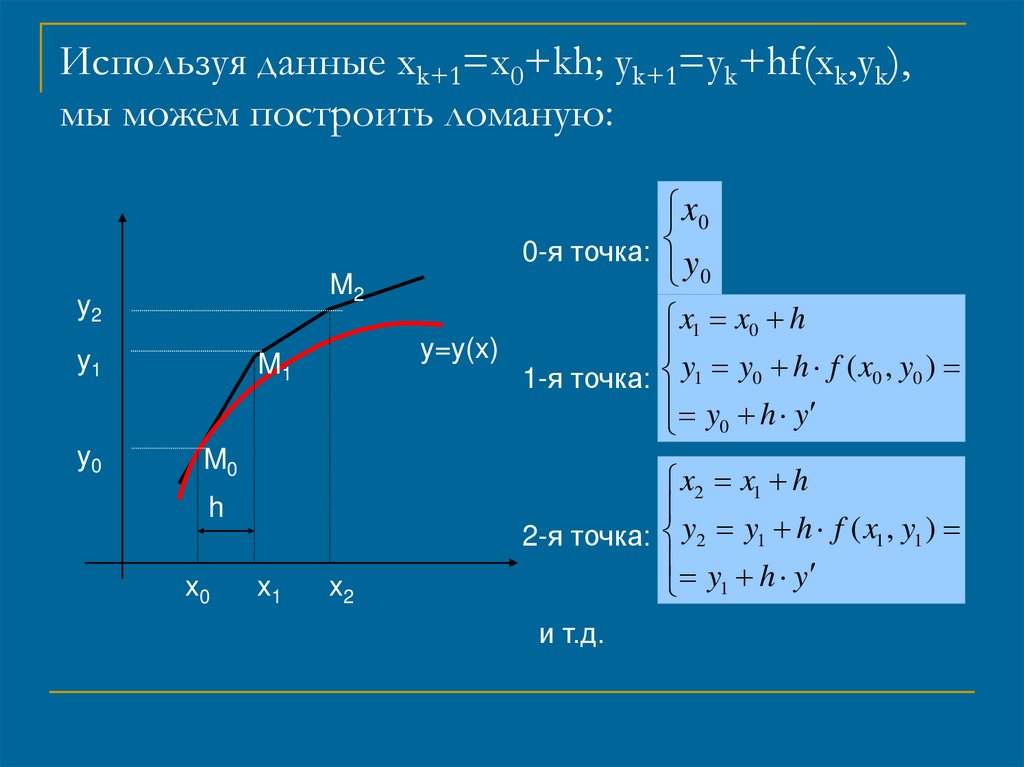
Используя данные xk+1=x0+kh; yk+1=yk+hf(xk,yk),
мы можем построить ломаную:
M2
y2
y1
y0
M1
M0
h
x0
x1
x2
x0
0-я точка: y
0
x1 x0 h
y=y(x)
1-я точка: y1 y0 h f ( x0 , y0 )
y h y
0
x2 x1 h
2-я точка: y2 y1 h f ( x1 , y1 )
y h y
1
и т.д.

15.

Пример: Используя метод Эйлера, найти решение
ДУ: y y x
при нач. условии y(0)=1 и h=0,1.
y x
x0 0, y0 1, h 0,1
1 0
1,1
1 0
1,1 0,1
y2 y1 h f ( x1 , y1 ) 1,1 0,1
1,183
1,1 0,1
1,183 0, 2
y3 y2 h f ( x2 , y2 ) 1,183 0,1
1, 254
1,183 0, 2
1, 254 0,3
y4 y3 h f ( x3 , y3 ) 1, 254 0,1
1,315
1, 254 0,3
y1 y0 h f ( x0 , y0 ) 1 0,1

16.

Сравнение метода Эйлера и численного
решения Maple
x0
x1
x2
x3
x4
…
0
0.1
0.2
0.3
0.4
…
Yi
1
(Эйлера)
1.1
1.183
1.254
1.315
….
Yi
(Maple)
1.091
1.168
1.233
1.290
…
xi
1

17.

Рассмотренный метод Эйлера имеет
существенные недостатки:
Мы пытаемся заменить кривую ломаной,
это даёт первый порядок точности по h.
Как видно из графика, ломаная неуклонно
отклоняется от кривой - метод неустойчив.
Необходим учёт кривизны искомой кривой
(метод Эйлера это сделать не позволяет).

18.

Исправленный метод Эйлера
Существуют различные модификации метода
Эйлера, повышающие его точность. Они
обычно направлены на то, чтобы более точно
определить переход от точки (xi,yi) в точку
(xi+1,yi+1). Метод Эйлера-Коши, например,
рекомендует следующий порядок
вычислений:
yi* 1 yi h f ( xi , yi )
f ( xi , yi ) f ( xi 1 , yi* 1 )
yi 1 yi h
2

19.

Графическая иллюстрация
исправленного метода Эйлера
L
yi+1
y=y(x)
tgα=f(xi,yi)
xi
xi+1
L2
L1

20.

Принцип, на котором основан метод
Эйлера-Коши, отражает факт учёта ещё
одного члена в разложении ряда Тейлора:
h2
y ( xi h) y ( xi ) h y ( xi )
y ( xi ) ...
2
Заменим в разложении y”(xi) соотношением:
y ( xi h) y ( xi )
y ( xi )
h
1
y ( xi h) y ( xi ) h ( y ( xi h) y ( xi ))
2
1
y ( xi h) y ( xi ) h ( f ( xi , yi ) f ( xi 1 , yi 1 ))
2
или

21.

Точность метода
Исправленный метод Эйлера согласуется с
разложением в ряд Тейлора до членов h2
являясь методом второго порядка, т.к.
отброшенный ряд T~h3. При подстановке в
алгоритм из-за умножения на 1/h, получим
R~h2.
Если в разложении сохранить следующие
члены разложения, будем иметь лучшее
приближение.

22.

Модифицированный метод Эйлера
В исправленном методе Эйлера усреднялись
наклоны касательных. Можно усреднять точки
по-другому.
h
h
yi 1 yi h f xi , y i yi , yi f ( xi , yi )
2
2
Этот метод согласуется с разложением в ряд
Тейлора до h2 включительно и является ещё
одним методом Рунге-Кутта второго порядка.

23.

Геометрическая иллюстрация
L
(xi+1,yi+1)
L2
L1
y=y(x)
(xi,yi)
xi
xi+h/2
xi+1

24.

Этот метод согласуется с разложением в ряд
Тейлора до h2 включительно и является ещё
одним методом Рунге-Кутта второго порядка.
Рассмотренные методы можно обобщить
формулой
h
h
y m 1 y m h (1 ) f ( xm , y m ) f xm
, ym
f ( x m , y m )
2
2
Это общая форма записи метода Рунге-Кутта
второго порядка. При =1/2 получаем
исправленный метод Эйлера, при =1 получаем
модифицированный метод Эйлера. Погрешность
R~h2. Её минимальное значение получается при
=2/3.

25.

Метод Рунге-Кутта
В рассмотренных методах для нахождения
следующего значения вычисляется
значение f два раза. Для повышения
точности количество точек увеличивается
(4 точки – для четвёртого порядка). Метод
Рунге-Кутта относится к методам
повышенной точности. Алгоритмически
мало чем отличается от метода Эйлера,
но требует большего объёма вычислений.

26.

Метод Рунге-Кутта
Этот метод учитывает члены ряда Тейлора
в разложении искомого решения y(x) до h4
включительно. Для этого при переходе от
xi к xi+1 необходимо учесть значения f(x,y)
в четырёх промежуточных точках.

27.

Метод Рунге-Кутта
k1 h f xi , yi
k1
h
k 2 h f xi , y i
2
2
k2
h
k 3 h f xi , y i
2
2
k 4 h f xi h, yi k 3
1
yi 1 yi (k1 2k2 2k3 k4 )
6

28.

Пример
Записать формулу перехода от i до i+1 точки
в случае, если f(x,y)=f(x).
h
h
yi 1 y i f ( xi ) 4 f xi f ( xi h)
6
2
Это формула Симпсона числовых
x h
интегралов:
i
y f ( x)dx
xi

29.

Погрешность на каждом шаге ~h5, а глобальная
погрешность (учитывая конечную точку) ~h4.
Один из недостатков методов Рунге-Кутта – в
отсутствии простых способов оценить
погрешность, а, следовательно, и правильно
выбрать шаг h.
Обычно используют грубое оценочное правило
Коллатца:
k 2 k3
Если отношение
k1 k2
становится велико (больше нескольких сотых), то
шаг h необходимо уменьшать.

30.

На практике для контроля точности
применяют следующий приём:
Если y2h – решение, полученное с шагом 2h,
yh – решение, полученное с шагом h,
то точность метода ε вычисляется по
формуле:
y2 h yh
15

31.

Методы Рунге-Кутта
Так как используется информация только об
очередной точке решения и не используется о
ранее найденных точках, то с помощью этих
методов можно начинать решение уравнения.
Однако при использовании этих методов
приходится многократно вычислять f(x,y) и
затрачивать много машинного времени.
Используя информацию об очередной точке, эти
методы позволяют легко менять величину шага h.
При использовании этих методов трудно получить
оценку погрешности.

32.

Постановка задачи для системы
ОДУ
Найти решение задачи Коши для системы ОДУ:
y1 f1 ( x, y1 ,..., yn ),
y f ( x, y ,..., y ),
2
2
1
n
................................
yn f n ( x, y1 ,..., yn )
y1 ( x0 ) y10 ,
0
y2 ( x0 ) y2 ,
...................
y ( x ) y 0 .
n
n 0

33.

Введем следующие векторные обозначения:
0
y
f
(
x
,
y
,...,
y
)
y
y
1
1
1
1
1
n
0
y2
y2
f 2 ( x, y1 ,..., yn )
y2
Y
,Y
, F ( x, Y )
, Y0
.......................
...
...
...
0
y
y
f
(
x
,
y
,...,
y
)
y
1
n
n
n
n
n
В таких обозначениях задача Коши принимает вид
Y F ( x, Y ), Y ( x0 ) Y0
такой же как для одного уравнения.

34.

Учитывая введенные обозначения, можно к векторному
уравнению применить любой из рассмотренных
методов.
Например,
y e
2 x,
2
z
2
y
z.
y2 z2
y (0) 0.5,
z (0) 1.
Применим метод Эйлера (с шагом h):
yi 1 yi h (e
2 xi ),
2
zi 1 zi h (2 yi zi ).
yi 2 zi 2

35.

Различают две группы численных
методов решения ДУ:
одноступенчатые методы, которые
используют для нахождения i+1 точки
информацию о кривой только в одной
предыдущей точке. В этом случае трудно
оценить допускаемую погрешность.
многоступенчатые методы. Для
повышения точности вычислений
очередной точки используют информацию
о нескольких предыдущих.

36.

Методы Адамса
Уточнение решения можно проводить не
привлекая дополнительные точки внутри
интервала интегрирования, а используя
решение в нескольких ранее найденных
точках сетки: n, n-1, n-2 и т.д.
Если использовать 2, 3, или 4 точки
предыдущие точки, мы получим разные
формулы. Все эти алгоритмы называют
методами Адамса.

37.

Методы Адамса
По двум предыдущим точкам строим
интерполяционный полином 1-й степени:
f ( , x ( ))
tn 1
t n t n 1
fn
tn
t n 1 t n
Заметим, что полином строится по точкам вне
промежутка интегрирования, т.е. проводится
экстраполяция
Проинтегрировав это выражение, получим
f n 1

38.

Явные методы Адамса
h
xn 1 xn (3 f n f n 1 )
2
2 точки
h
xn 1 xn (23 f n 16 f n 1 5 f n 2 )
12
3 точки
h
xn 1 xn (55 f n 59 f n 1 37 f n 2 9 f n 3 ) 4 точки
24

39.

Неявные методы Адамса
h
xn 1 xn ( f n f n 1 )
2
2 точки Метод
трапеций
h
xn 1 xn (5 f n 1 8 f n 5 f n 1 )
12
3 точки
h
xn 1 xn (9 f n 1 19 f n 5 f n 1 f n 2 )
24
4 точки

40.

Методы Адамса
► Требуют лишь однократного вычисления
функции на каждом шаге.
► Не являются самостартующими.
► Погрешность для 2-х точек h3,
для 3-х точек h4.

41.

Методы прогноза и коррекции
Методы прогноза и коррекции называются
так, потому что вначале
«предсказывается» (прогнозируется)
значение yi+1, а затем используется тот
или иной метод для корректировки» этого
значения. Причем корректировку можно по
одной и той же формуле выполнять
многократно.

42.

Рассмотрим один из вариантов метода
прогноза и коррекции. Для прогноза
используется формула второго порядка
точности:
(0)
i 1
y
yi 1 2hf ( xi , yi )
где верхний индекс (0) означает исходное
приближение к yi+1, т.е. предсказанное
значение. С помощью этой формулы
нельзя вычислить y1.

43.

Коррекция значения осуществляется
по формуле:
(1)
i 1
y
h
yi ( f ( xi , yi ) f ( xi 1 , yi(0)
1 ))
2
которую можно применить многократно:
(k )
i 1
y
h
yi ( f ( xi , yi ) f ( xi 1 , yi( k1 1) ))
2

44.

Итерационный процесс прекращается, когда
yi( k1 1) yik 1 .
Оценку погрешности метода приведем без
доказательства:
R
(k )
1 (0)
yi 1 yi( k1) .
5

45.

Оценка получается такой простой и не
зависит явно от h потому, что погрешности
прогноза и коррекции одного порядка (h3).
В отличие от других рассмотренных
методов этот метод дает погрешность в
качестве побочного продукта вычислений.