Алгебра и анализ

1. Алгебра и анализ

2. Основные правила игры

• Формула оценивания: Контрольная работа: Контрольная работа*0.260 + Работа на семинарах:
Активность * 0.070 + Работа на семинарах: Активность * 0.070 + Итоговая контрольная работа по всему
курсу: Контрольная работа * 0.600
• Правила округления: Оценивание результатов производится по 10 балльной шкале. Итоговая оценка I
получается округлением до ближайшего целого числа значения выражения, полученного по
формуле: \par I=0.26*K+0.14*W+0.6*E, \par где K–балл за контрольную работу; W –балл за активность
на семинарах, определяемый выступлениями у доски; E –балл за итоговую экзаменационную (по
всему курсу) контрольную работу в конце второго модуля.
• Правила выставления автомата: Если бал, учитывающий текущую активность в 1,2 модулях, и
вычисляемый по формуле \par N=0.7*K+0.3*W \par не меньше 8, то преподаватель имеет право
предложить студенту засчитать его в качестве оценки за итоговую контрольную работу и в качестве
итоговой оценки по всему курсу.
• Правила пересдачи: Первая пересдача экзаменационной работы предусматривает выполнение
письменной работы, по заданиям схожим с экзаменационной работой и оценка по дисциплине
выставляется по той же формуле, что и до пересдач. При пересдаче на комиссию все предыдущие
оценки аннулируются, и оценка, полученная на комиссии, выставляется в качестве итоговой оценки по
дисциплине

3. Особо рекомендуемая литература

• Сборник задач по высшей математике : учеб. пособие для
соц.упр. специальностей, Логвенков, С. А.
• Математика для экономических специальностей : учебник, rus
• : рус.Красс М.С.
• Сборник задач по высшей математике 1 курс: К.Н. Лунгу, В.П.
Норин, Д.Т. Письменный

4.

5. Предел последовательности

6. Понятие числовой последовательности

ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ хn называется
упорядоченное счетное множество чисел х
.
,
х
,
х
,
х
......
1
2
3
4
Числа хn , где n=1,2,3,4,….ЭЛЕМЕНТЫ(члены) последовательности,
символ х n -ОБЩИЙ ЧЛЕН ПОСЛЕДОВАТЕЛЬНОСТИ, а число n-его
НОМЕР.

7. Примеры числовых последовательностей

8. Определение предела последовательности

• Определение(нестрогое) :
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ –это число А, к которому члены
последовательности стремятся при неограниченном возрастании
номера n.
обозначение:
х
A при n
n
x A
lim
n
n

9. Определение предела последовательности

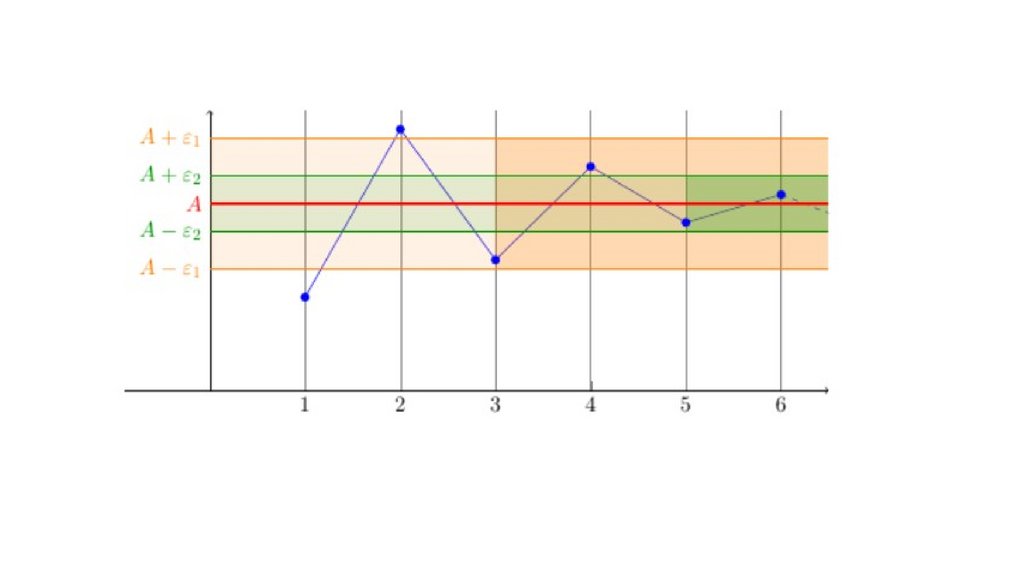
• Определение:
Число А называется ПРЕДЕЛОМ ПОСЛЕДОВАТЕЛЬНОСТИ хn , если
для любого ε>0 найдется натуральное число N(ε)(зависящее от ε),
что при всех n>N, будет выполняться неравенство xn A<ε.
( >0 :
>N xn A<ε) lim
x
A
N
n
n
n

10.

11. Свойства пределов последовательностей

1.
2.
4.
3.
5.

12. Известные пределы последовательностей

13. Известные пределы последовательностей

Второй замечательный предел

14. Неопределенности

• Выше среди пределов уже встречались такие, где ответ был не очевиден и сразу
воспользоваться арифметическими правилами не было никакой возможности. В таком
случае говорят, что имеется НЕОПРЕДЕЛЕННОСТЬ, а преодоление этих трудностей (как
правило путём каких-то преобразований выражения) называется раскрытием
неопределённостей. Вот некоторый список наиболее часто встречающихся
неопределённостей:
Решения задач, как правило, сводятся к изучению методов раскрытия
неопределённостей.

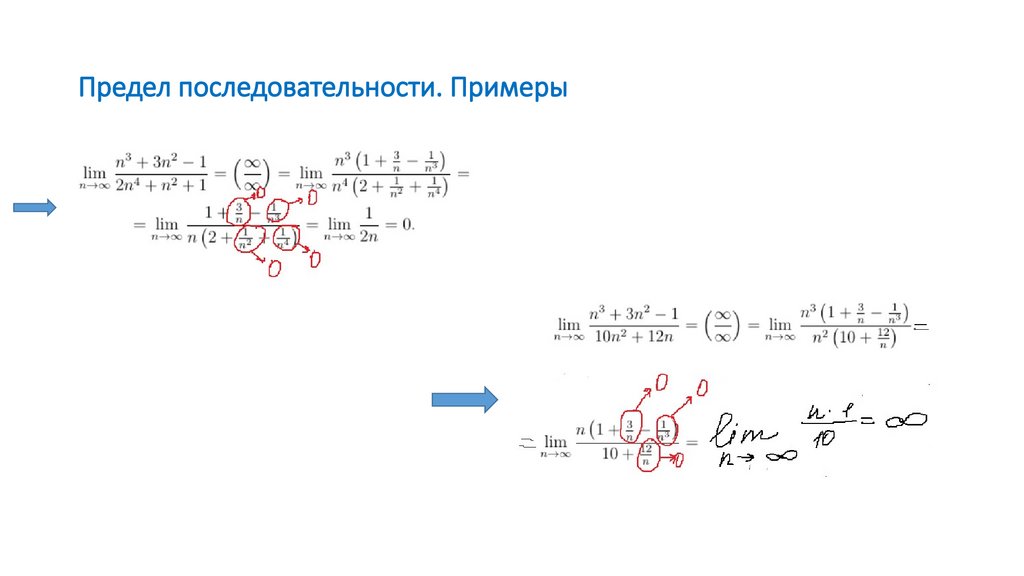
15. Предел последовательности. Примеры

16. Предел последовательности. Примеры

17. Предел последовательности. Примеры.

18. Предел последовательности. Примеры.

19. Предел функции

20. Предел функции

• Для определения пределов удобно пользоваться поведением
соответствующих функций. Ничто не мешает теперь вместо
натуральных аргументов рассматривать произвольный аргумент .
По сравнению с пределами последовательностей, появятся всего
пара отличий:
• во-первых, х может теперь стремиться к минус бесконечности, а,
значит, необходимо будет каждый раз указывать знак
бесконечности
• во-вторых, теперь придётся следить за тем, чтобы функция была
определена при всех достаточно больших (или достаточно малых,
если стремление к −∞) значениях аргумента и учитывать поведение
при всех х .

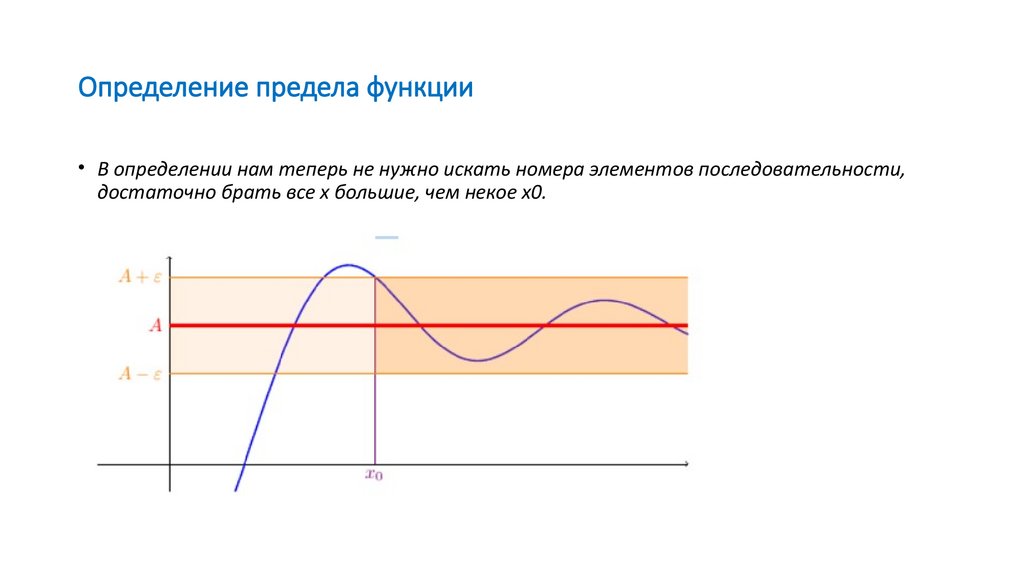
21. Определение предела функции

• В определении нам теперь не нужно искать номера элементов последовательности,
достаточно брать все х большие, чем некое х0.

22. Определение предела функции.

23. Значения пределов некоторых элементарных функций.

24. Свойства пределов функций.

25. Пределы функций. Примеры.

26. Пределы функций. Примеры.

27. Пределы функций. Примеры.

28. Пределы функций. Примеры.