Лекция к работе 2

1.

Лекция №3
Рассматриваемые темы:
Тема 6. Задача Коши. Численные методы решений ОДУ первого порядка. Метод
Эйлера.
Тема 7. Локальная и глобальная ошибки. Устойчивость и сходимость метода
Эйлера.
1

2.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Рассмотрим обыкновенное дифференциальное уравнение первого
порядка в общем виде:
dy
f ( x, y),
dx
x [ a, b]
f ( x, y ) – некоторая функция, в общем случае, нелинейная.
Порядок ОДУ зависит от порядка производной от искомой функции.
dy
– производная первая, значит и порядок ОДУ – тоже первый
dx
2

3.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Для полной постановки задачи не хватает граничных или начальных условий.
В чем отличие граничных условий (ГУ) от начальных (НУ)?
начальные
граничные
dy
f (t , y )
dt
dy
f ( x, y),
dx
время
координата
Да данном этапе нам неважно что характеризует
координата, по которой проводится дифференцирование.
3

4.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Для полной постановки задачи не хватает граничных или начальных условий.
Как определить количество граничных условий?
dy
x.
Рассмотрим простейшее ОДУ первого порядка:
dx
2
Решение: y
x
C
2
– это общее решение
константа, определяемая из ГУ
Пример ГУ: при x0 = 2, y0 = 1. Значит C = –1
x2
y
1 – это частное решение
2
4

5.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Как определить количество граничных условий?
Количество граничных определяется порядком ОДУ.
Для ОДУ первого порядка необходимо одно граничное условие.
5

6.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Полная постановка задачи.
dy
f ( x, y)
dx
x [ a, b]
Граничное условие (одно): y (a) y0
Это задача Коши
6

7.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Решение ОДУ будем искать в дискретном наборе точек xi,
совокупность которых образует расчетную сетку, т.е.
решение будет выглядеть как yi y ( xi ).
Ось ОХ
x0
x1
x2
x3
…
xi
…
xn
Составим конечно-разностную схему. Запишем данное уравнение для
узла с номером i (x = xi):
dy
f ( xi )
dx x xi
7

8.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Введем обозначения:
dy
y ' ( xi )
dx x xi
индекс, не степень!
y ( xi ) y i
Применим правила конечно-разностных аппроксимаций первых
производных для левой части уравнения.
Левая разность: y ' ( xi )
y y
h
i
i 1
Выражаем yi через yi–1:
подставляем в ОДУ
y i y i 1
f ( xi , yi )
h
y i y i 1 hf ( xi , yi )
8

9.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Проделаем то же самое для формул правой и центральной разностей.
y i 1 y i
Правая разность: y' ( xi )
h
y i 1 y i
f ( xi , yi )
h
y i 1 y i hf ( xi , yi )
y i 1 y i 1
Центральная разность: y' ( xi )
2h
y i 1 y i 1
f ( xi , yi )
2h
y i 1 y i 1 2hf ( xi , yi )
Проделанные операции называются построением разностных схем.
Решение ОДУ первого порядка с использованием данных расчетных формул называется
методом Эйлера, а алгоритм их получения – метод конечных разностей.
9

10.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Итого мы получили три рабочих формулы для решения ОДУ первого порядка:
1.
y
i 1
явная схема
y hf ( xi , yi ) Значения функции на текущем шаге вычисляется
i
на основе значений функций, взятых с
предыдущего шага.
i
i 1
y
y
hf ( xi , yi )
2.
3. y i 1 y i 1 2hf ( xi , yi )
неявная схема
Значения функции на текущем шаге вычисляется
на основе значений функций, взятых как с
предыдущего шага, так и с текущего.
уточненная схема
10

11.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Пример.
Дано ОДУ первого порядка:
dy
x 3 5.
dx
Решить численно методом конечных разностей данное уравнение в
промежутке от 1(a) до 5(b) и сравнить численное решение с
аналитическим.
Постановка задачи полная?
Нет, не хватает граничных условий: x1 = 1, y1 = 10.
11

12.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Шаг 1. Вычисление шага сетки. Будем использовать 21 узел. В
данном примере есть только одна координата x, поэтому сетка
будет одномерная. Вычислим шаг по формуле: h=L/(n – 1).
b a 5 1
h
0.2
n 1 21 1
12

13.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Шаг 2. Нахождение набора значений xi : xi 1 x1 ih
где i = 1, 2 … 10, x1 = a = 1.
Шаг 3. Составим численную схему решения для явной и
неявной схем:
y
i 1
y h( xi 5)
i
3
y i y i 1 h( xi 5)
3
явная схема
неявная схема
13

14.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Шаг 4. Вычисление.
явная схема
y 2 y 1 h( x1 5)
3
y 3 y 2 h( x2 5)
3
y n y n 1 h( xn 1 5)
3
Граничное условие
Внимание! Именно при вычислении значения функции в следующем
за первым узле необходимо граничное условие. В противном случае
отсутствия граничного условия, ОДУ нельзя решить однозначно.
14

15.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Шаг 4. Вычисление.
неявная схема
y 2 y1 h( x2 5)
3
y 3 y 2 h( x3 5)
3
y n y n 1 h( xn 5)
3
Граничное условие
Внимание! Именно при вычислении значения функции в следующем
за первым узле необходимо граничное условие. В противном случае
отсутствия граничного условия, ОДУ нельзя решить однозначно.
15

16.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
y 2 y1 h( x2 5)
вычисляем в этом узле
3
x1
x2
x3
x4
…
xi
Ось ОХ
…
xn
Граничное условие
y 3 y 2 h( x3 5)
3
вычисляем в этом узле
x1
x2
x3
x4
…
xi
…
Ось ОХ
xn
Решение уже известно
16

17.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Шаг 5. Найдем аналитическое решение интеграла ОДУ.
dy
x3 5
dx
y ( x 3 5)dx x 4 / 4 5 x C – общее решение
Для нахождения константы С воспользуемся ГУ:x1 = 1, y1 = 10
10 1/ 4 5 C
частное решение:
C 4.75
y x 4 / 4 5 x 4.75
17

18.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Шаг 6. Вычисление относительной погрешности численного и
аналитических решений (в процентах):
100 n y
n i 1
( численное)
( xi ) y ( аналитическое ) ( xi )
y ( аналитическое ) ( xi )
18

19.

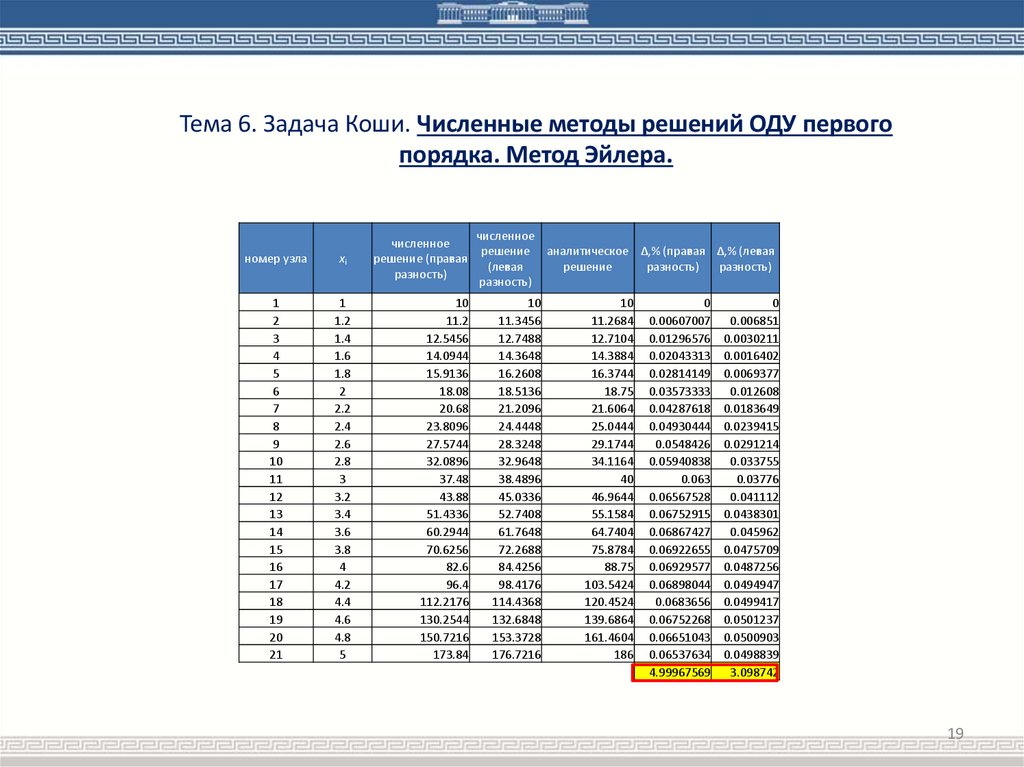
Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
номер узла
xi
численное
решение (правая
разность)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
1
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
3
3.2
3.4
3.6
3.8
4
4.2
4.4
4.6
4.8
5
10
11.2
12.5456
14.0944
15.9136
18.08
20.68
23.8096
27.5744
32.0896
37.48
43.88
51.4336
60.2944
70.6256
82.6
96.4
112.2176
130.2544
150.7216
173.84
численное
решение аналитическое Δ,% (правая Δ,% (левая
(левая
решение
разность)
разность)
разность)
10
11.3456
12.7488
14.3648
16.2608
18.5136
21.2096
24.4448
28.3248
32.9648
38.4896
45.0336
52.7408
61.7648
72.2688
84.4256
98.4176
114.4368
132.6848
153.3728
176.7216
10
11.2684
12.7104
14.3884
16.3744
18.75
21.6064
25.0444
29.1744
34.1164
40
46.9644
55.1584
64.7404
75.8784
88.75
103.5424
120.4524
139.6864
161.4604
186
0
0.00607007
0.01296576
0.02043313
0.02814149
0.03573333
0.04287618
0.04930444
0.0548426
0.05940838
0.063
0.06567528
0.06752915
0.06867427
0.06922655
0.06929577
0.06898044
0.0683656
0.06752268
0.06651043
0.06537634
4.99967569
0
0.006851
0.0030211
0.0016402
0.0069377
0.012608
0.0183649
0.0239415
0.0291214
0.033755
0.03776
0.041112
0.0438301
0.045962
0.0475709
0.0487256
0.0494947
0.0499417
0.0501237
0.0500903
0.0498839
3.098742
19

20.

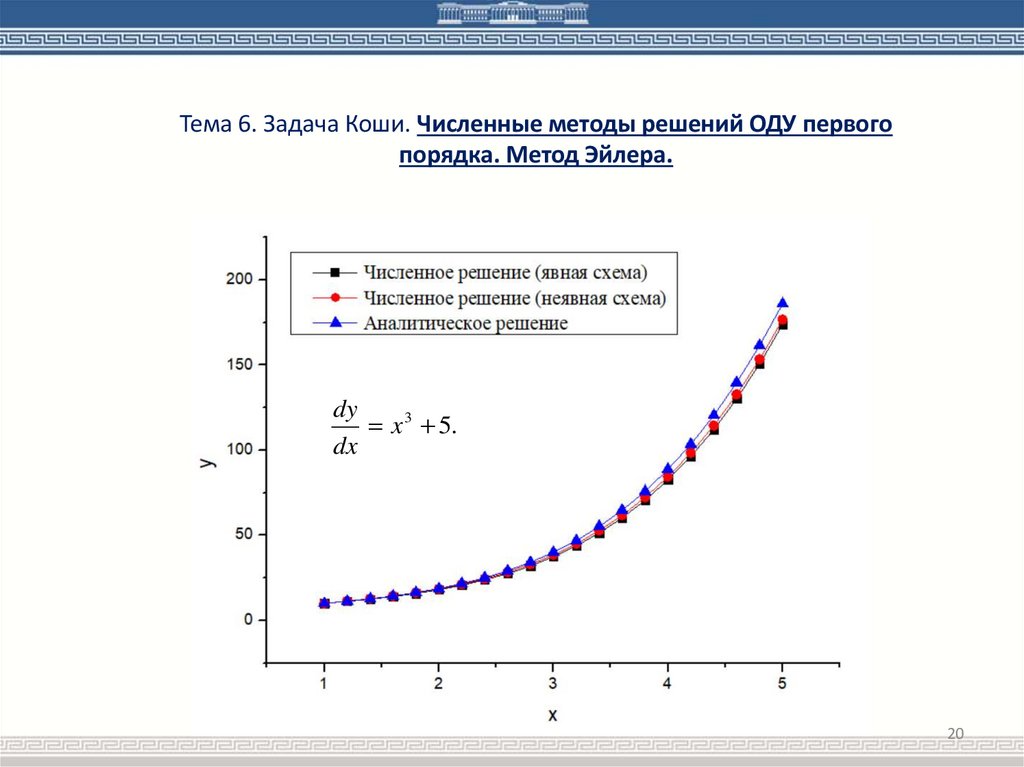
Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
dy
x 3 5.
dx
20

21.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Немного более сложная ситуация возникает при использовании
уточненной схемы.
y i 1 y i 1 2hf ( xi , yi )
y 2 y 0 2hf ( x1 , y1 )
Ось ОХ
x1
x2
x3
x4
…
xi
…
xn
В узле 2 , т.е. в точке, ближайшей к граничной, не можем использовать
данное уравнение, т.к. информации об узле с номером «0» отсутствует.
21

22.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Как это лечится?
левая или правая разности
y i 1 y i 1 2hf ( xi , yi )
y y h( x2 5)
2
1
3
уточненная схема
x1
x2
x3
x4
…
xi
…
Ось ОХ
xn
22

23.

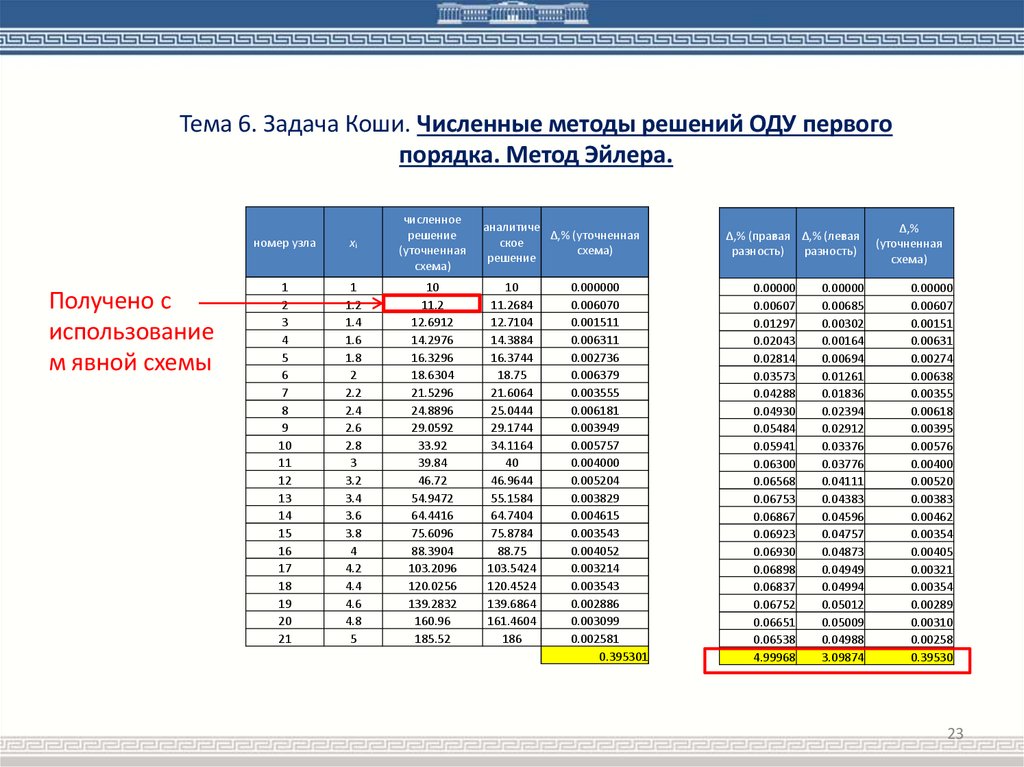
Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Получено с
использование
м явной схемы
номер узла
xi
численное
решение
(уточненная
схема)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
1
1.2
1.4
1.6
1.8
2
2.2
2.4
2.6
2.8
3
3.2
3.4
3.6
3.8
4
4.2
4.4
4.6
4.8
5
10
11.2
12.6912
14.2976
16.3296
18.6304
21.5296
24.8896
29.0592
33.92
39.84
46.72
54.9472
64.4416
75.6096
88.3904
103.2096
120.0256
139.2832
160.96
185.52
аналитиче
Δ,% (уточненная
ское
схема)
решение
10
11.2684
12.7104
14.3884
16.3744
18.75
21.6064
25.0444
29.1744
34.1164
40
46.9644
55.1584
64.7404
75.8784
88.75
103.5424
120.4524
139.6864
161.4604
186
0.000000
0.006070
0.001511
0.006311
0.002736
0.006379
0.003555
0.006181
0.003949
0.005757
0.004000
0.005204
0.003829
0.004615
0.003543
0.004052
0.003214
0.003543
0.002886
0.003099
0.002581
0.395301
Δ,% (правая Δ,% (левая
разность)
разность)
0.00000
0.00607
0.01297
0.02043
0.02814
0.03573
0.04288
0.04930
0.05484
0.05941
0.06300
0.06568
0.06753
0.06867
0.06923
0.06930
0.06898
0.06837
0.06752
0.06651
0.06538
4.99968
0.00000
0.00685
0.00302
0.00164
0.00694
0.01261
0.01836
0.02394
0.02912
0.03376
0.03776
0.04111
0.04383
0.04596
0.04757
0.04873
0.04949
0.04994
0.05012
0.05009
0.04988
3.09874
Δ,%
(уточненная
схема)
0.00000
0.00607
0.00151
0.00631
0.00274
0.00638
0.00355
0.00618
0.00395
0.00576
0.00400
0.00520
0.00383
0.00462
0.00354
0.00405
0.00321
0.00354
0.00289
0.00310
0.00258
0.39530
23

24.

Тема 6. Задача Коши. Численные методы решений ОДУ первого
порядка. Метод Эйлера.
Замечание: в общем случае граничное условие может быть задано в
промежутке [a, b], а не на концах отрезка.
Граничное условие
Ось ОХ
x1
x2
x3
x4
y 3 y 4 hf ( x3 , y3 )
x5
x6
…
xn
y 5 y 4 hf ( x4 , y4 )
явная схема
24

25.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Вопрос 1: какова точность метода Эйлера?
y i y i 1 y ' ' ( xi 1 )
y ' ( xi )
h
h
2
y i y i 1 hf ( xi , yi )
y ' ' ( xi 1 ) 2
h
2
левая разность
остаточный член
неявная схема
y i 1 y i y ' ' ( xi 1 )
y ' ( xi )
h
h
2
y i 1 y i hf ( xi , yi )
y ' ' ( xi 1 ) 2
h
2
правая разность
остаточный член
явная схема
25

26.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Вопрос 1: какова точность метода Эйлера?
y ' ' ( xi 1 ) 2
Остаточный член≈
h
2
вторая степень
Ошибка (погрешность), возникающая на одном итерационном
шаге, называется локальной.
Провести вычисление функции в одном узле сетки означает провести
одну итерацию.
Вывод: локальная погрешность
метода Эйлера для явной и неявной
схем имеет второй порядок
y i y i 1 hf ( xi , yi )
y ' ' ( xi 1 ) 2
h
2
y i 1 y i hf ( xi , yi )
y ' ' ( xi 1 ) 2
h
2
26

27.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Вопрос 1: какова точность метода Эйлера?
y i 1 y i 1 y ' ' ' ( xi ) 2
y ' ( xi )
h
2h
6
центральная разность
y ' ' ' ( xi ) 3
h
6
остаточный член
y i 1 y i 1 2hf ( xi , yi )
уточненная схема
y ' ' ' ( xi ) 3
h
6
третья степень
Вывод: локальная погрешность метода Эйлера для
уточненной схемы имеет третий порядок
27

28.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Вопрос 1: какова точность метода Эйлера?
Но не все так просто…
локальная
ошибка
Задача из примера.
y 2 y1 h( x1 5) O(h 2 )
3
y 3 y 2 h( x2 5) O(h 2 )
3
тут погрешность уже сидит
y 4 y 3 h( x3 5) O(h2 )
y n y n 1 h( xn 1 5) O(h2 )
тут погрешность уже
сидит с предыдущих
шагов
тут погрешность, которая
копилась n-1
итерационных шагов
3
3
28

29.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Вопрос 1: какова точность метода Эйлера?
Итерация в
последней точке
y n y n 1 hf ( xn 1 , yn 1 ) O(h 2 )
тут погрешность, которая
копилась n-1
итерационных шагов
В результате к последнему итерационному шагу, т.е. в последней
точке сетки, мы накапливаем локальную ошибку. Накопленная
ошибка называется глобальной.
29

30.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Вопрос 1: какова точность метода Эйлера?
y i y i 1 hf ( xi 1 , yi 1 ) O(h 2 )
локальная
ошибка
Глобальная ошибка
Ось ОХ
x1
x2
x3
x4
…
xi
…
xn
30

31.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Вопрос 2: каков порядок глобальной ошибки метода Эйлера?
Не происходит ли такого большого «лавинообразного» накопления локальной
ошибки, что к последнему итерационному шагу решение «развалится» и мы в
конечном итоге получим некорректное решение?
К этому важнейшему фундаментальному вопросу в теории построении
численных схем относятся такие понятия как
устойчивость и сходимость.
Принято говорить так: является ли численная разностная
схема устойчивой и сходимой?
31

32.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Определение 1
Устойчивость – это свойство алгоритма решения задачи или самой
задачи, при котором малое изменение входных данных приводит к
малому изменению результата.
На вопрос устойчивости стоит исследовать как (а) саму задачу (уравнение, ОДУ
или что то другое), так и (б) сам метод решения (численную схему).
32

33.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Примеры неустойчивых задач.
( x a) n
Пусть n = 10. Если погрешность в измерении (x-a) составит 10-10, то
результат изменится на величину примерно равную 10-1.
Вывод: задача неустойчива к малым возмущениям.
33

34.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Определение 2
Пусть yi – численное решение, полученное на сетке; пусть y*(xi) –
точное (идеальное) решение.
а) Разностная схема называется сходящейся, если
y * ( xi ) y i 0 при i стремящемся к бесконечности.
б) Разностная схема называется сходящейся с порядком k, если
выполняется неравенство:
y * ( xi ) y i Ch k при i стремящемся к бесконечности.
34

35.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Итак, можно сформулировать 2 цели.
1) Выяснить, является ли метод Эйлера сходящимся?
2) Определить порядок глобальной ошибки метода Эйлера.
35

36.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
Введем параметр εi , характеризующий различия между точным и
численным решением на i – ом шаге:
i y * ( xi ) y i
Выразим εi+1 через εi .
Точное решение y*(xi) представим с помощью формулы Тейлора, а
численное решение с использованием явной схемы
y * ' ' ( xi ) 2
y ( xi 1 ) y ( xi ) y ' ( xi )h
h – точное решение
2!
*
*
*
y i 1 y i hf ( xi , yi )– численное решение
36

37.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
C
i 1 y ( xi 1 ) y
*
i 1
y * ' ' ( xi ) 2
y ( xi ) y ' ( xi )h
h y i hf ( xi , yi )
2!
*
*
i y * ( xi ) y i
L
f (x , y ) f (x , y ) h f ' (x , y ) ( y (x ) y ) h f ' (x , y ) h
i
*
i
*
i
i
y
i
i
i
i
y
i
i
i
i
i 1 i i Lh Ch2
i 1 i (1 Lh) Ch2
Модуль суммы меньше или равен сумме модулей
37

38.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
i 1 i (1 Lh) Ch 2
A
B
i 1 i A B
В узле 1, в котором задано ГУ , 1 0
В узле 2: 2 B
В узле 3: 3 AB B
2
2
В узле 4: 4 A B AB B ( A A 1) B
В узле n: n ( An 2 An 3 ...1) B
38

39.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
В узле n: n ( An 2 An 3 ... A 1) B
Что это за конструкция?
Это геометрическая прогрессия!
Поскольку n – большое число, то без потери общности примем, что
n 2 n
A
n 2
A
n 3
An 1
... A 1
A 1
An 1
n
B
A 1
39

40.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
An 1
n
B
A 1
Сделаем обратную замену.
A 1 Wh 1 1
B Ch 2
n
длина сетки
n
L
h
L
h
(1 Wh) 1
Ch 2
Wh
1
Вспомним первый замечательный предел: lim( 1 ) e при 0
1
n
n – большое число, значит 1/α стремится
к нулю. Удовлетворяет требованию
40

41.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
L
h
(1 Wh) 1
n
Ch 2
Wh
WL
Wh
(1 Wh)
n
Wh
n (eW L 1)
1
Ch
2
lim( 1 )
1
e
Ch
W
Ответы на вопросы: 1) выяснить, является ли метод Эйлера сходящимся?
Да! Метод Эйлера является сходящимся с первым порядком по шагу. Его
можно смело использовать для построения численных схем
Это глобальная ошибка, накопленная к n-му итерационному шагу.
41

42.

Тема 7. Локальная и глобальная ошибки. Устойчивость и
сходимость метода Эйлера.
L
h
(1 Wh) 1
n
Ch 2
Wh
WL
Wh
(1 Wh)
n
Wh
n (eW L 1)
1
Ch
2
lim( 1 )
1
e
Ch
W
Ответы на вопросы: 2) Определить порядок глобальной ошибки метода Эйлера.
Порядок глобальной ошибки Эйлера – первый. Порядок глобальной ошибки на
один порядок меньше локальной ошибки. Это общее правило для
большинства численных схем.
42

43.

Спасибо за внимание
43