3сем_Лк 2_Однород и лин ДУ 1 пор_ДУ Бернулли — копия

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины II
Кафедра высшей математики
Лекция 2. Однородные и линейные ДУ 1–го порядка.
Уравнение Бернулли.
25.09.2025
г. Санкт-Петербург
2025
1|14

2.

Однородные ДУ 1-го порядка
F1 ( x, y )dx F2 ( x, y )dy 0 (1 Когда можно разделить переменные в ДУ?
)
Функция f(x,y) называется однородной
функцией n–го измерения
относительно переменных х и у, если при любом ≠0 справедливо тождество
Пример 1.
f ( x, y) f ( x, y)
n
f ( x, y) x2 2 y 2 xy – однородная функция 2-го измерения
y x
f ( x, y )
y x
f ( x, y ) 2 x 2 2 2 y 2 2 xy 2 ( x 2 2 y 2 xy) 2 f ( x, y)
– однородная функция нулевого измерения
y x
y x
0
f ( x, y ) f ( x, y)
f ( x, y )
y x
y x
ДУ (1) называется однородным, если функцииF1 ( x, y ) иF2 ( x, y )
однородные одинакового измерения
2|14

3.

Решение однородного ДУ 1-го порядка
сведение к ДУ с разделяющимися переменными
F1 ( x, y ) однородные n-го
F2 ( x, y ) измерения
Замена
х≠0
y xt(x)
dy tdx xdt
F1 ( x, y )dx F2 ( x, y )dy 0
x n f 2 (t )(tdx xdt)
x n f1 (t )
dx
f 2 (t )dt
0
x
f1 (t ) tf 2 (t )
могли
потерять:
F1 ( x, tx) x n F1 (1, t ) x n f1 (t )
F2 ( x, tx) x n F2 (1, t ) x n f 2 (t )
f1 (t ) tf 2 (t ) dx xf 2 (t )dt 0
x f1 (t ) tf 2 (t ) 0
dx f 2 (t )dt C
x
f1 (t ) tf 2 (t )
f1 (t ) tf 2 (t ) 0.
t = a – действительный корень
х = 0 (у 0)
у=ах (х 0)
решения
могут содержаться в формуле
общего интеграла или быть особыми
3|14
f 2 (t )dt
ln x
C.
f1 (t ) tf 2 (t )
берется по переменной t
обратная замена
t = y/x
общий интеграл ДУ (1)

4.

dy
(2)
f ( x, y ) однородное ДУ относительно х и у
dx однородная функция
y
нулевого измерения
xy
x
y
зависит только
y 2
y
2
2
от
отношения
f ( x, y) 1f ( x, y) f 1,
y
x
y
аргументов
1
x
x
x
t t ( x) y / x
dt
dx
dt
x
'
t
t
'
x
f
(
t
)
y
x f (t ) t
dt
y xt(x)
(3) y ( x) f
dx
x
f (t ) t
x
Пример 2. Решить ДУ
Решение.
dx
dx
dt
С
f (t ) t x
y
y
y e x
y
Замена
t
x
x
t xt t e xt e
t
e
t
y
x ln x C
4|14
dt
dx
t
t
х
e e dt
dx
х
e t ln x C

5.

Пример 3. Решить ДУ ( x 2 2 xy)dy 2 y 2 dx 0
F1 ( x, y )
2
dy
2y
2
dx
x 2 xy
В качестве зависимой
переменной можно
принимать х
F2 ( x, y )
dx x 2 2 xy
0
2
dy
2y
– однородные 2-го измерения
x yt( y )
Диф–ем по у:
t х/ у
x t yt
1 2
t yt t t 0
2
ДУ с разделяющимися переменными:
2dt dy
2
0 ln y ln С
2
y
t
t
, где C 0
2y
ln y
ln C
x
2y
у Сe x
общий интеграл
С R
Решение у=0 (х 0)
получается из общего при С=0
Решение х=0 (у 0)
было потеряно при переходе к ДУ с разделяющимися переменными
5|14

6.

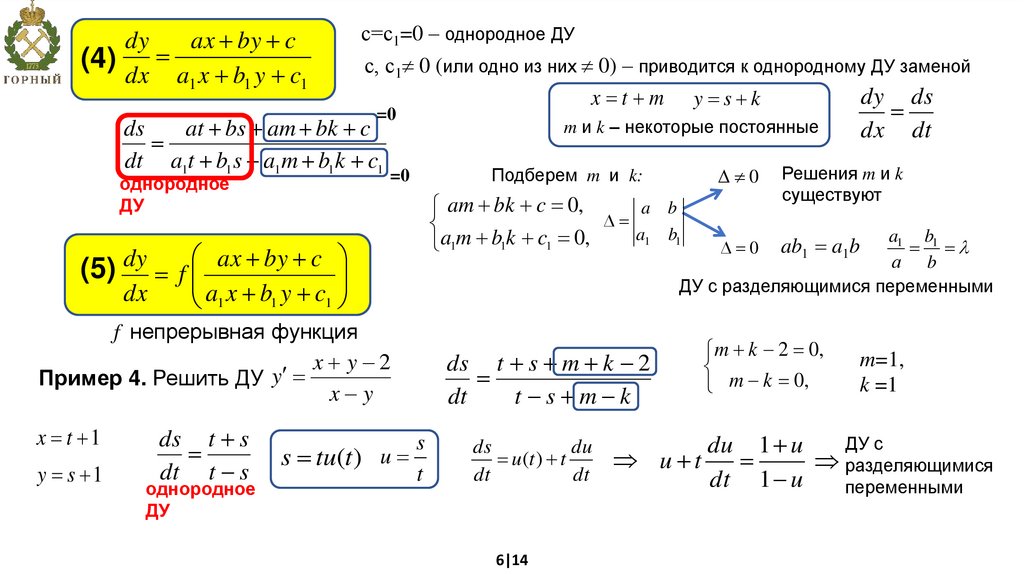
dy
ax by c
(4)
dx a1 x b1 y c1
с=с1=0 – однородное ДУ
с, с1 0 (или одно из них 0) – приводится к однородному ДУ заменой
dy ds
x t m y s k
=0
ds
at bs am bk c
dt a1t b1 s a1m b1k c1
однородное
ДУ
=0
ax by c
dy
(5) f
dx
a1 x b1 y c1
f непрерывная функция
x y 2
Пример 4. Решить ДУ y
x y
x t 1
y s 1
ds t s
dt t s
однородное
ДУ
s
s tu(t ) u
t
m и k – некоторые постоянные
0
Подберем m и k:
a b
am bk c 0,
a1 b1
a1m b1k c1 0,
dx
dt
Решения m и k
существуют
a1 b1
а b
ДУ с разделяющимися переменными
ds t s m k 2
dt
t s m k
ds
du
u (t ) t
dt
dt
6|14
0
ab1 a1b
m k 2 0,
m k 0,
m=1,
k =1
ДУ с
du 1 u
u t
разделяющимися
dt 1 u
переменными

7.

Линейное ДУ 1-го порядка
линейное относительно
(6) y ( x) p ( x) y ( x) q ( x)
искомой функции
и ее 1-ой производной
непрерывные функции в (a, b)
Уравнение Бернулли
однородное ДУ
q ( x) 0
q ( x) 0
неоднородное ДУ
(7) y ( x ) p( x ) y ( x ) q( x ) y ( x )
n
z ( x) y
n 1
n ≠ 0,
n≠1
1
y( x) z 1 n
1
y
1 n
n
z 1 n z
1
1 n
n
1
n
z 1 n z p z 1 n q z 1 n
z ( x) 1 n pz 1 n q (6)
7|14

8.

Метод Бернулли. Решение ДУ (6) и (7)
у=u·v , u = u(х), v = v(х) – диф-мые функции
y ( x) p( x) y ( x) q( x) v du u dv pv q
Решение у(х) ищем в виде:
u′v + uv′
dx
u·v
dx
dv
pv 0
Функцию v подбираем так, чтобы
dx
p ( x ) dx
dv
pdx ln v ln C p( x)dx v( x) Сe
v
du
dx
p ( x ) dx
v
q du q u( x) C q( x)e
dx
dx
v
(8) y( x) e
8|14
p ( x ) dx
v e
pdx
p ( x ) dx
dx .
C q ( x )e

9.

Пример 5. Решить ДУ
Можно сразу
воспользоваться
формулой (8) или
проделать все шаги
решения
у=u·v
dv 2 xdx
v 1 x2
2 xy
2
y
1
x
2
1
x
p(x)
q (x)
2 xuv
2
u v uv
1 x
2
1 x
2x
2
v
u v u v'
1
x
2
1
x
=0
d (1 x 2 )
ln v
2
1 x
Одно из
2
решений: v 1 x
ln(1 x )
2
(1 x 2 )u ' 1 x 2 u ' 1
u x C
Общее решение:
9|14
y (1 x )( x C )
2

10.

Линейное ДУ 1-го порядка с постоянными коэффициентами
dy
ay b
dx
Метод Бернулли или разделение переменных:
C 2 aC1
dy
1
dy
b ay b ay dx ln b ay x C1 ln b ay ax C 2
a
dx
1 C2
b
b 1 C2 ax
ax
C2 ax
С e
e
y y Ce
b ay e
a
a
a a
Общее решение
Пример 6. Решить ДУ
dy
dx
dy
dy
C
x
y y 1
dx
dx ln y 1 x C y 1 Ce где C e
1 y
Пример 7. Решить ДУ
y
1 y2
y 1 x y
.
2
нелинейное ДУ
у 1
y
dx y 1 x y 2
xy
dx y 1 y 2
dy
1
x y
x
2
2
2
2
dx dx / dy
dy
1 y
dy
1 y
1 y
1 y
линейное ДУ относительно
1
x( y) u( y)v( y) x u v uv
y
х
и
производной
dx/dy
x
Самостоятельно решить ДУ методом Бернулли
10|14

11.

Уравнение Бернулли
n
y ( x ) p( x ) y ( x ) q( x ) y ( x ) y f ( x, y )
f ( x, y) q( x) y p( x) y
n
Теорема о существовании и
единственности решения ДУ
q( x) и p( x)
n = 0 – линейное ДУ непрерывны в (a, b)
f y ( x, y) – непрерывна
нет особых
решений
0 < n < 1 – решение у = 0
f y ( x, y) – не существует при у = 0
особое
n > 0– есть решение у = 0
n > 1 – решение у = 0 частное
11|14

12.

Пример 8. Решить задачу Коши y y tg x sec x
Линейное ДУ
у=u·v
y(0) 0
u v uv uv tg x sec x
u v u (v v tg x) sec x
v v tg x 0
dv
tg xdx
v
u sec x sec x u x C
ln v ln C ln cos x
v sec x
y sec x( x C )
0 sec 0(0 C ) 0 1(0 C ) C 0
Решение задачи Коши:
12|14
x
y x sec x
cos x

13.

Правда ли, что…
1. ДУ P( x, y)dx Q( x, y)dy 0 является однородным?
x
2. ДУ y cos является однородным?
y
2 xy
3. ДУ y 2
интегрируются при помощи подстановки y t ( x) x ?
2
x y
x 2 y 1
4. ДУ y
однородное?
2x 4 y 3
2 y
2y
5. ДУ y
является уравнением Бернулли?
2
x cos x
dy
6. ДУ
sin( x) y ln( x) y n при n 1 есть уравнение с разделяющимися переменными?
dx
7. ДУ y 2 dx (2 xy 3)dy 0 является линейным?
8. ДУ Бернулли сводится к линейному заменой z
1
n 1
?
y
y
9. ДУ y 1 является одновременно и линейным, и однородным?
x
2
dy
dy
10. ДУ x 2 x y 0 сводится к однородному уравнению ?
dx
dx
13|14

14.

Спасибо за внимание
Кафедра высшей математики;
Санкт-Петербургский горный
университет императрицы
Екатерины II;
199106, Санкт-Петербург,
Васильевский остров, 21 линия д.2;
Тел.: +7(812) 328-82-31;
E-mail: kafmatem@spmi.ru
14|14