Похожие презентации:
Дифференциальные уравнения первого порядка
1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА (лекция №11 мен)
2. ПРОСТЕЙШИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
План1. Основные понятия
2. Решение дифференциальных уравнений
I-го порядка
3. Решение дифференциальных уравнений IIго порядка
4. Задачи на составление диф.уравнений
3. 1. Основные понятия
Определение:Уравнения,
содержащие
неизвестную
функцию, аргумент этой функции и ее
производные
или
дифференциалы,
называются дифференциальными.
В общем виде Д.У. можно записать так:
F ( x, y, y , y ,..., y
(n)
) 0
4.
• Решить дифференциальное уравнение• Решить Д.У. значит найти функцию, которая
при подстановке в Д,У., обращает его в
тождество, т.е. найти у(х)
• Например, решением дифференциального
уравнения радиоактивного распада
dN
N
dt
будет функция:
N(t) =N0e- t
5. Виды уравнений:
• Обыкновенное Д.У. - если искомаяфункция есть функция одного аргумента.
• Д.У. в частных производных – если
искомая функция зависит от нескольких
аргументов и дифференциальное
уравнение содержит ее частные
производные по этим аргументам
6. например
x 3 dy y 3 dx 0;xy y (2 x xy) y
2
y 6 y 8 y 0;
2
y
1
4 y
2 2 2 8 2m
2 2 2 E E p 0
2
х
y
z
h
S
1 S
2
2
2
х
v t
2
2
7.
• Порядок дифференциального уравнения• Порядком дифференциального уравнения
называется порядок старшей производной
или дифференциала, содержащегося в этом
уравнении.
i
dФ
dt
2
d s
m 2 F
dt
8.
• Процесс нахождения решенийдифференциального уравнения называется
интегрированием дифференциального
уравнения.
• Поэтому решение Д.У. иногда называют
общим интегралом
9. Виды решений Д.У.
• Различают общее и частное решениядифференциального уравнения.
• Общим решением дифференциального
уравнения (ОРДУ) называется такое его
решение , которое содержит столько
независимых произвольных постоянных ,
каков порядок этого уравнения.
• Если общее решение дифференциального
уравнения получают в неявном виде , то оно
называется общим интегралом.
10.
• Чтобы найти частное решение Д.У. (ЧРДУ),должны быть известны так называемые
начальные условия.
• Например, для дифференциального
y y
уравнения
• ОРДУ будет :
y Ce
x
y ( 0) 2
• а ЧРДУ будет при условии
y 2e
x
11. 2. Решение дифференциальных уравнений I-го порядка
• Расмотрим решение некоторых видов Д.У.:• - уравнения I –го порядка с
разделяющимися переменными
• - однородные Д.У. I –го порядка
12. Д.У. I-го порядка с разделяющимися переменными
• К таким уравнениям относятся уравнениявида
f1 ( x) 1 ( y)dx f 2 ( x) 2 ( y)dy 0
Путем алгебраических преобразований
данное уравнение приводят к уравнениям
вида
Ф( y ) dy F ( x) dx
13.
• После интегрирования уравненияФ( y ) dy F ( x) dx
• находим общее решение дифференциального
уравнения или общий интеграл
Ф
(
y
)
dy
F
(
x
)
dx
• откуда выражаем
• где ОРДУ:
y f ( x, c )
y f ( x, c )
14. Например: xydx + (x + 1)dy = 0.
• Разделим переменные(x + 1)dy = – xydx
dy
xdx
y
x 1
• проинтегрируем обе части уравнения
dy
xdx
y
x 1
15.
dy( x 1 1)dx
y x 1
dy
1
x 1
y x 1 x 1 dx
dy
1
y x 1 1 dx
ОИДУ:
ОРДУ:
ln y ln( x 1) x ln C
y C ( x 1)e
x
16. Запишем алгоритм решения Д.У. 1 порядка с разделяющимися переменными:
• 1. Выразить производную из уравнения• 2. Записать производную через
дифференциалы
• 3. Разделить переменные (с функцией
налево, с аргументом направо)
• 4. Проинтегрировать обе части Д.У.
• 5. Из вида первообразных выразить
функцию – это будет ОРДУ
17. Д.У. I-го порядка однородные
• Однородными Д.У. называются уравнения,в которых производная является функцией
y
от y . То есть
х
y ` f ( )
x
• Решаются эти уравнением путем замены
переменной
18.
• Решаются эти уравнением путем заменыпеременной
y ux
• u y
Отсюда
x
• Тогда
du
y u x x u
x u
dx
• После такой подстановки уравнение
превращается в уравнение с
разделяющимися переменными
19. Например:
x yy
x y
Например:
• Это однородное уравнение, т.к.
1 y / x
y
1 y / x
• Обозначим
y
u
x
Отсюда
du
y u x x u
x u
dx
• Тогда
• Уравнение будет иметь вид
du
1 u
x u
dx
1 u
y ux
20. Решаем уравнение
du1 u
x
u
dx
1 u
du
1 u u u2
x
dx
1 u
(1 u ) du
dx
2
1 u
x
du
2
1 u
udu
2
1 u
dx
x
du
1 u
x u
dx
1 u
21. Теперь интегрируем
12
arctg (u ) ln( 1 u ) ln x C
2
y
arctg
x
1
ln( 1 ( y / x) 2 ) ln x C
2
Т.к.выразить «У» невозможно, то мы
получили ОИДУ
22. ДУ первого порядка линейные неоднородные
y p( x) y q( x)Используем замену переменной
y uv
y u v uv .
Подставив значения y и y в уравнение, получим:
u v uv p( x)uv q( x)
u v u v p( x)v q( x)
23.
u v u v p( x)v q( x)• Если выбрать v(x) так, чтобы выражение,
стоящее в скобках, обратилось в нуль, т.е.
v p( x)v 0
• то для второй функции u(x) получится
уравнение
u v ( x ) q( x ).
• После этого найдем
y v( x) u( x, C).
24. ДУ в полных дифференциалах
P( x, y )dx Q( x, y )dy 0Если предположить, что это полный
дифференциал какой-то функции U(x,y),
То
u
u
P ( x, y )
x
Причем, U(x,y)=const и
P Q
y
x
Q ( x, y )
y
25. алгоритм
• Проверить P Qy
x
• Из области определения выбрать x0
• Вычислить Q ( x 0, y )
• Найти
x
y
x0
y0
y0
u ( x, y ) P( x, y )dx Q( xo , y )dy
• Приравнять найденное значение константе





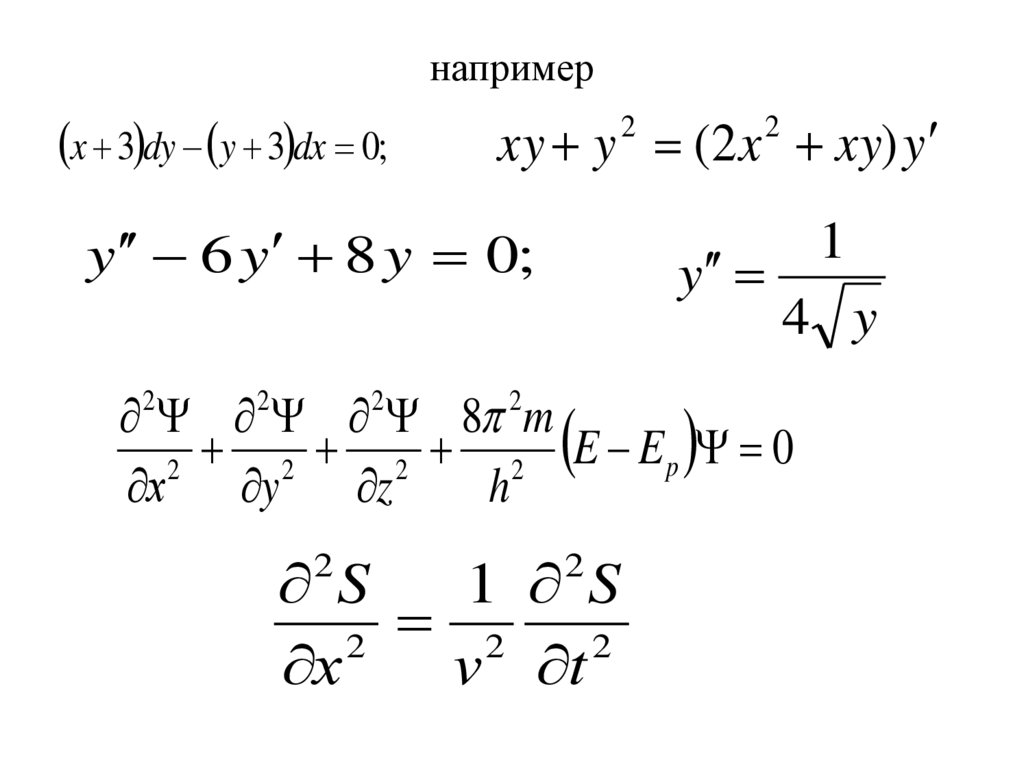








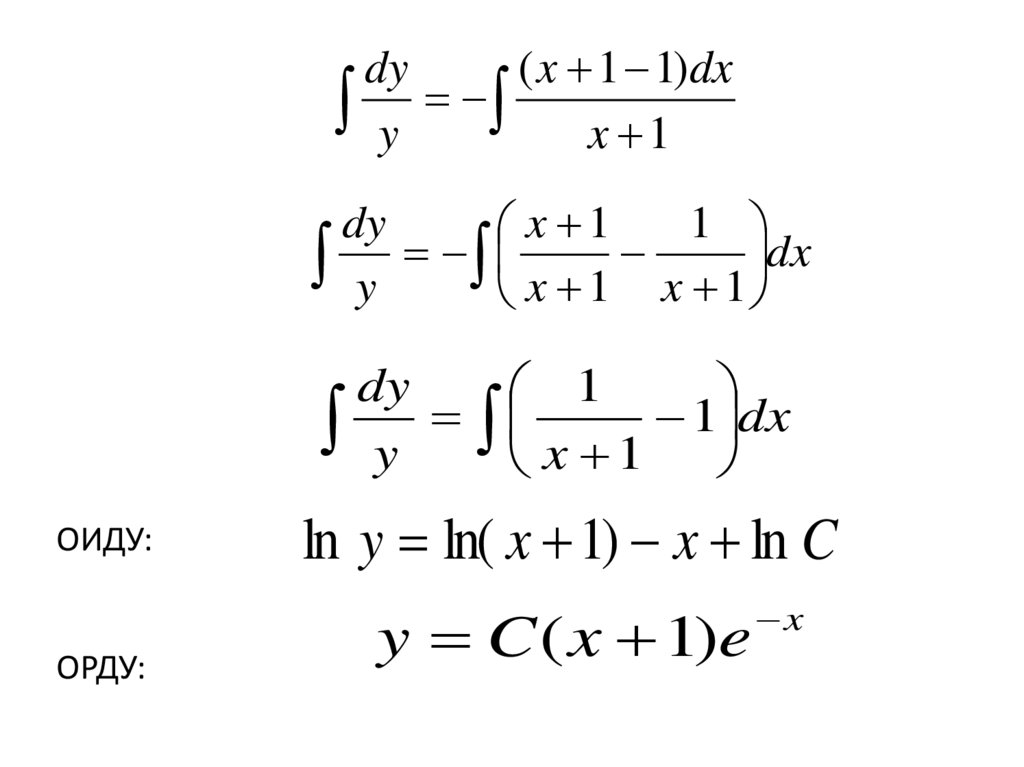










 Математика
Математика








