Лекция 1

1. Начертательная геометрия

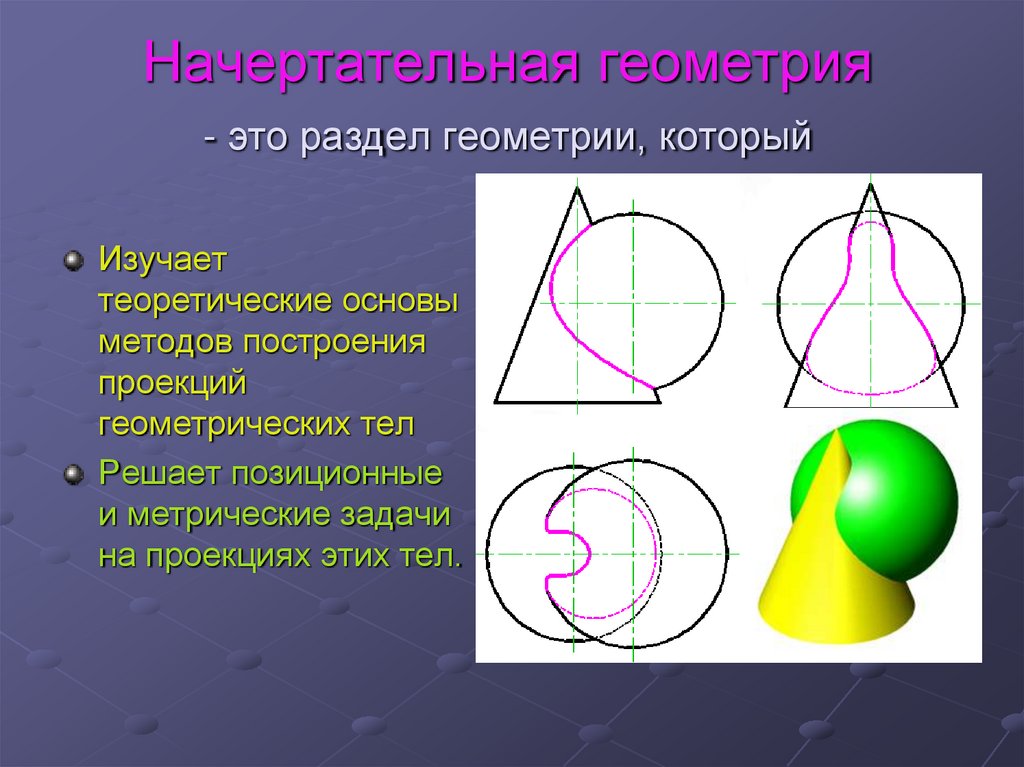
Лекция 1

2. Начертательная геометрия - это раздел геометрии, который

Изучает
теоретические основы
методов построения
проекций
геометрических тел
Решает позиционные
и метрические задачи
на проекциях этих тел.

3. Основные понятия

Точка - не имеет размеров, является
результатом пересечения двух прямых или
трех плоскостей (вершина тетраэдра)
Прямая – имеет одно измерение, является
результатом пересечения двух плоскостей
Плоскость – имеет два измерения.
Геометрическая фигура – определяется как
любое множество точек.

4. Обозначения

Ф,Г,∆,∑ А,В,С Поверхности Точки
П1 П2 П3 Плоскости
проекций
а,b,с,d – α,β, γ Линии
Углы
А1,а1,Ф1 А2,а2,Ф2 А3,а3,Ф3
– проекции – проекции – проекции
точки,
прямой,
поверхности
на П1
точки,
прямой,
поверхности
на П2
точки,
прямой,
поверхности
на П3

5. Символы

(АВ) – прямая,
проходящая через
точки А и В
[AB] – отрезок прямой
IADI – расстояние
между точками А и
D
- принадлежность
элемента
- включение
II - параллельные
┴ - перпендикулярные
• - скрещивающиеся
= - результат
построения
- «И»
- если…, то….
- пересечение

6. Задачи начертательной геометрии

Прямая задача – создание плоского
чертежа объекта.
Обратная задача – возможность по
плоскому чертежу восстановить
пространственный вид объекта.

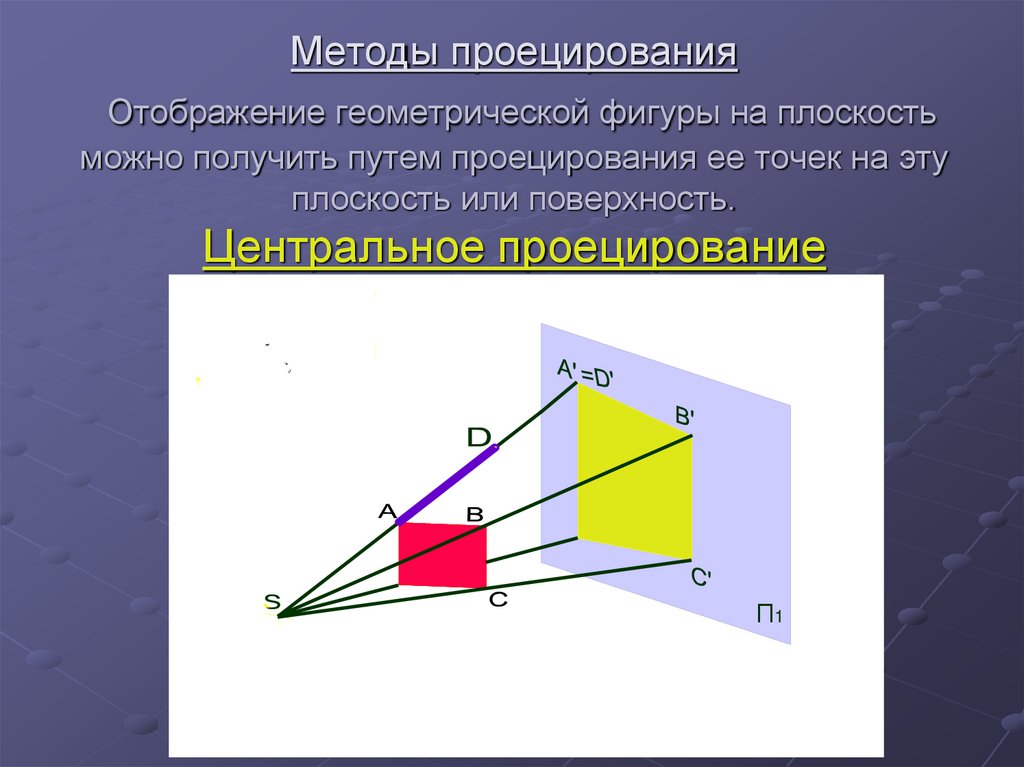
7. Методы проецирования Отображение геометрической фигуры на плоскость можно получить путем проецирования ее точек на эту

плоскость или поверхность.
Центральное проецирование
П1

8. Параллельное проецирование

S
S
А
Ï
А1
В
'
'
С
В1
'
С1
П1

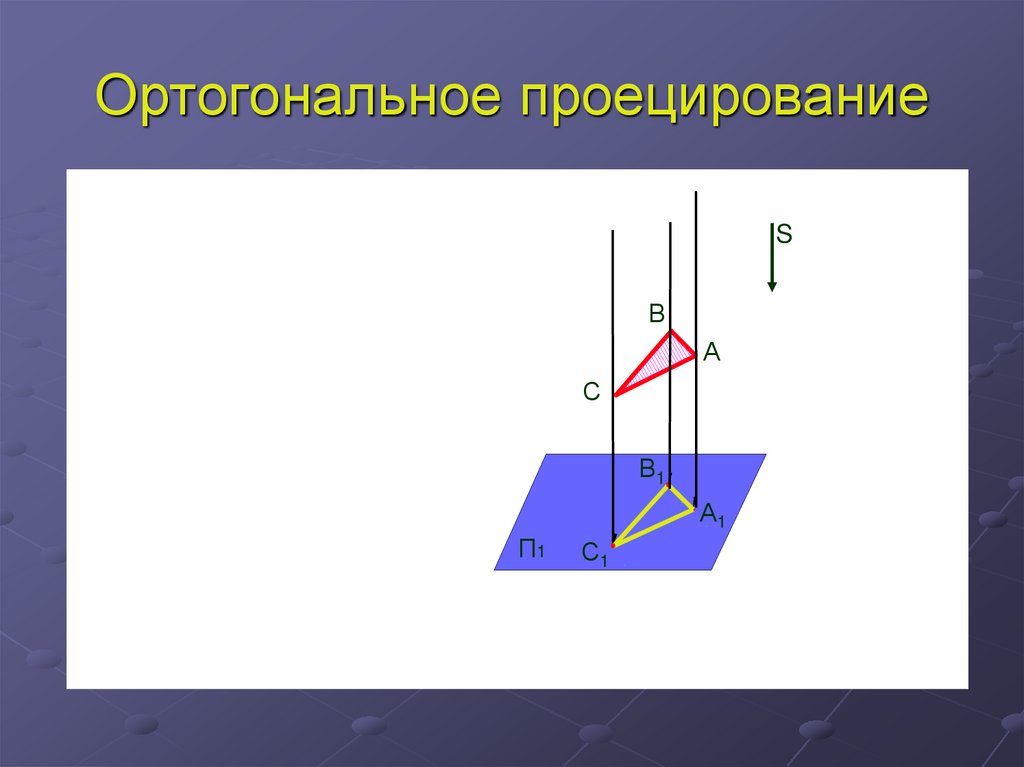
9. Ортогональное проецирование

В
А
С
Ï
В1
'
'
А1
П1
'
С1
S
S

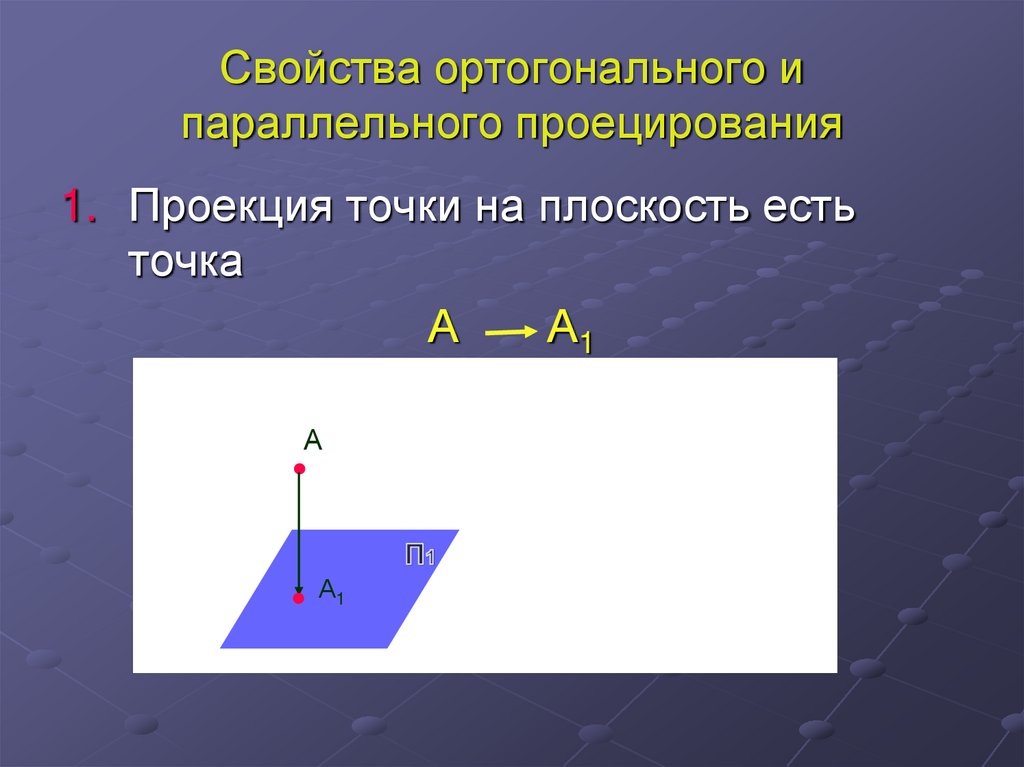
10. Свойства ортогонального и параллельного проецирования

1. Проекция точки на плоскость есть
точка
А
А1
А
А1

11. Проекцией прямой в общем случае является прямая. Она вырождается в точку, если прямая параллельна направлению проецирования l

2.
Проекцией прямой в общем случае
является прямая.
Она вырождается в точку, если
прямая параллельна направлению
проецирования
l
l1
l
l
l1
l1

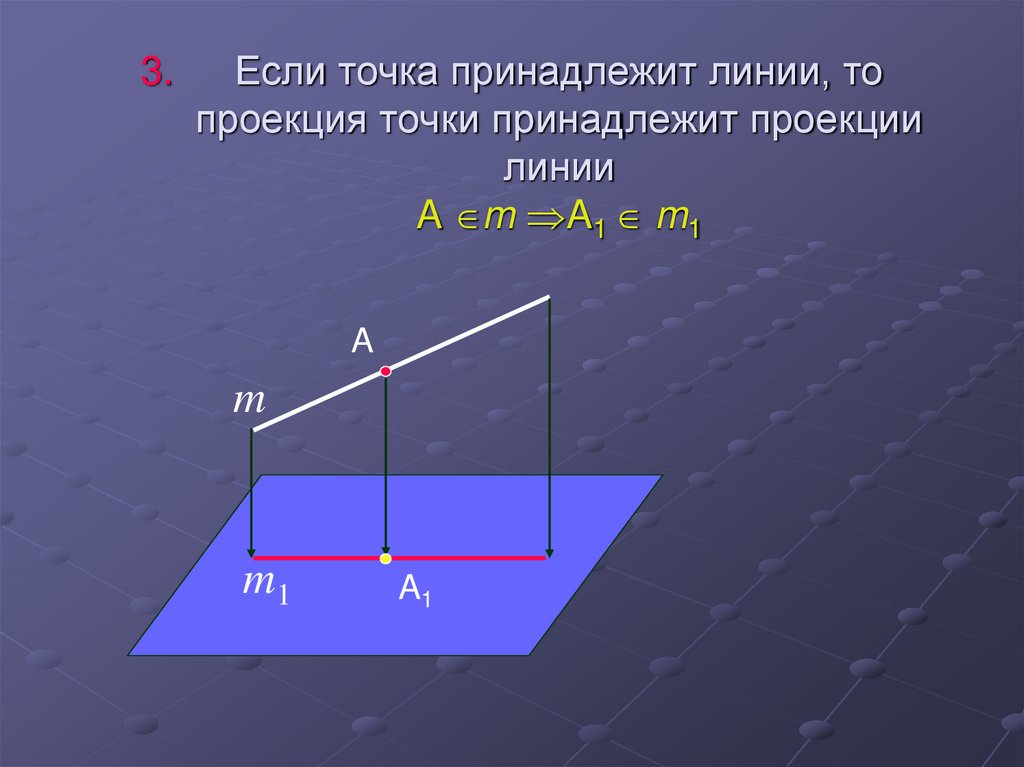
12. Если точка принадлежит линии, то проекция точки принадлежит проекции линии A m A1  m1

3.
Если точка принадлежит линии, то
проекция точки принадлежит проекции
линии
A m A1 m1
A
m
m1
A1

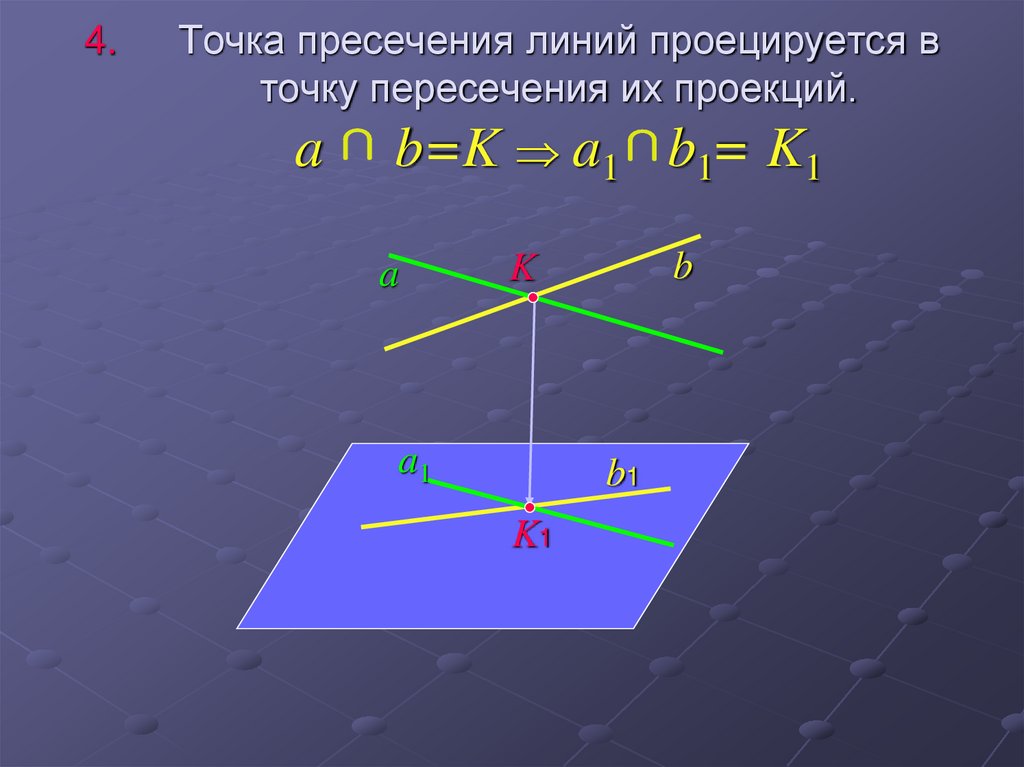
13. Точка пресечения линий проецируется в точку пересечения их проекций. a b=K  a1 b1= K1

4.
Точка пресечения линий проецируется в
точку пересечения их проекций.
a
b=K a1 b1= K1
a
b
K
a1
b1
K1

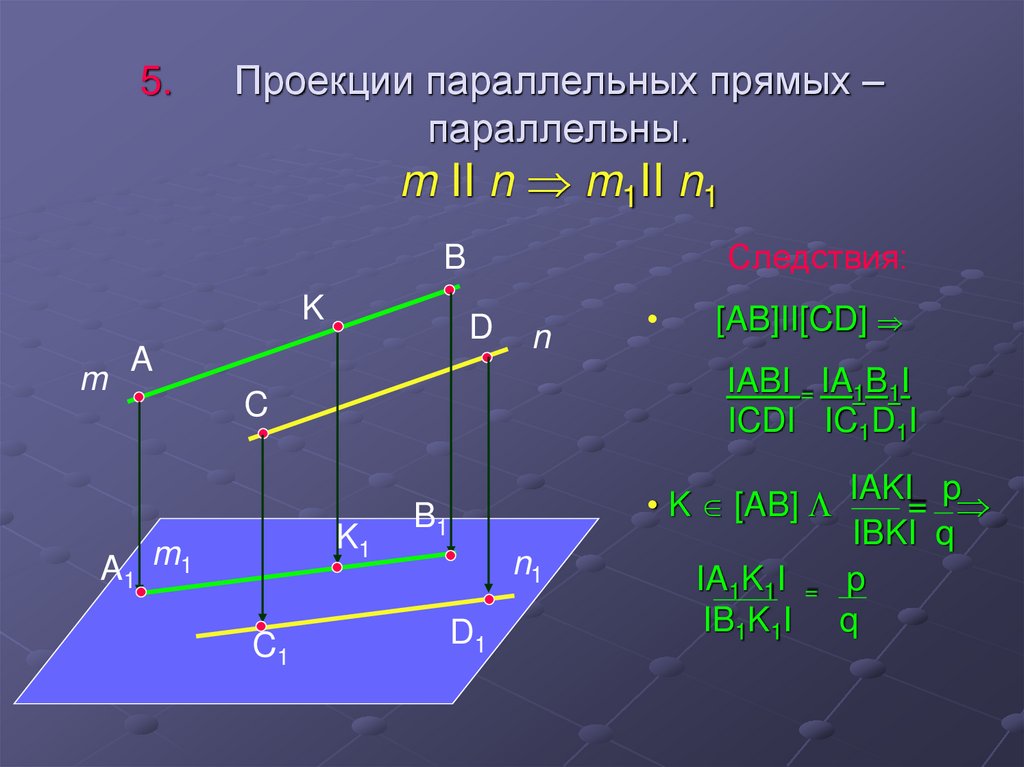
14. Проекции параллельных прямых – параллельны. m II n  m1II n1

5.
Проекции параллельных прямых –
параллельны.
m II n m1II n1
Следствия:
B
K
m
D
A
n
K1
C1
[AB]II[CD]
IABI = IA1B1I
ICDI IC1D1I
C
A1 m1
B1
n1
D1
• K [AB] IAKI= p
IBKI q
IA1K1I = p
IB1K1I q

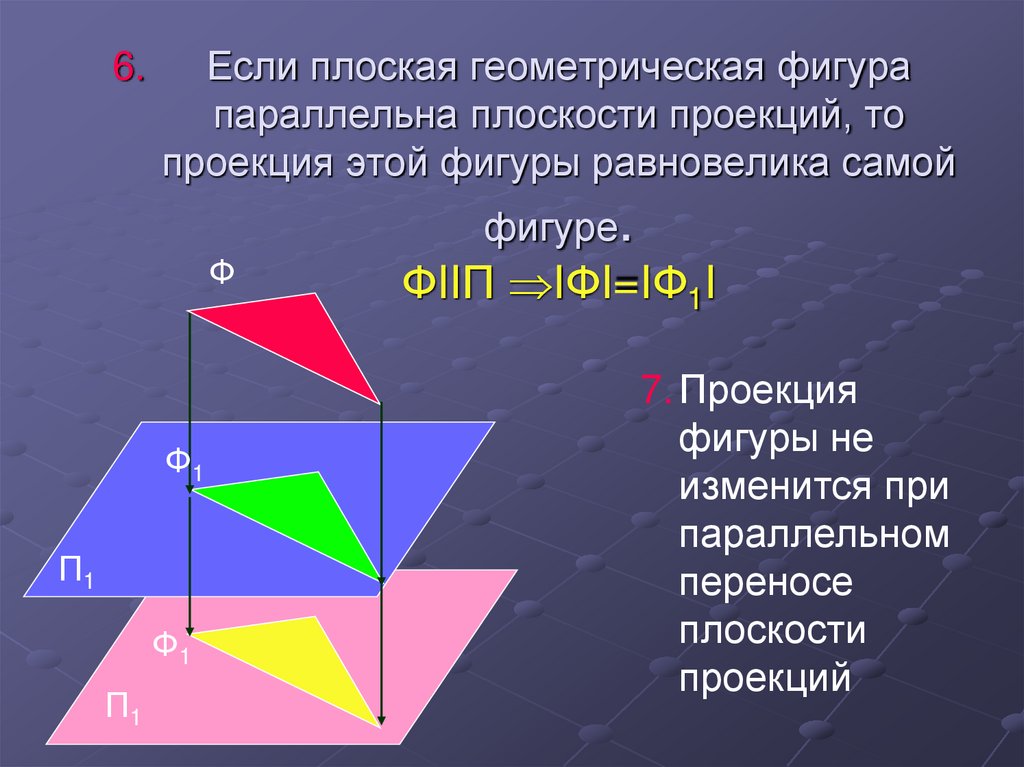
15. Если плоская геометрическая фигура параллельна плоскости проекций, то проекция этой фигуры равновелика самой фигуре. ФIIП

6.
Если плоская геометрическая фигура
параллельна плоскости проекций, то
проекция этой фигуры равновелика самой
фигуре.
Ф
Ф1
П1
Ф1
П1
ФIIП IФI=IФ1I
7. Проекция
фигуры не
изменится при
параллельном
переносе
плоскости
проекций