L_6

1. Глава II. Векторная алгебра и аналитическая геометрия

2. Переход из одного базиса к другому

пример
пропустить страницу

3.

Матрица перехода
Рассмотрим два базиса векторного пространства V(3)
Е = {ēi} = e1 e2 e3 , и F = {f̅i} = f1 f 2 f3
пропустить 15 клеточек
ОПР. Матрица T составленная из коэффициентов разложения,
называется матрицей перехода от старого базиса ē1, ē2, ē3 к новому
базису f̅1 , f̅2 , f̅3 .
11 12 13
T 21 22 23
31 32 33
ОПР*. Матрицей перехода Т от базиса Е базису F называется
матрица, столбцами которой служат координаты векторов
нового базиса в старом базисе.
Тогда в матричной форме система (1) имеет вид
F=ET
- формула перехода от старого базиса к новому

4.

Формула перехода от нового базиса к старому
E = F T -1
Как изменятся координаты вектора при переходе от одного
базиса к другому?

5.

ТЕОРЕМА 7 (связь координат вектора в разных базисах).
Пусть ē1, ē2, ē3 и f̅1 , f̅2 , f̅3 два базиса во множестве V(3) .
Причем имеют место равенства
f̅1 = τ11ē1 + τ21ē2 + τ31ē3 ,
f̅2 = τ12ē1 + τ22ē2 + τ32ē3 ,
f̅3 = τ13ē1 + τ23ē2 + τ33ē3 .
Если вектор ā имеет в базисе ē1,ē2,ē3 координаты
{α1 , α2, α3}, а в базисе f̅1 , f̅2 , f̅3 – координаты {β1 , β2, βn},
то справедливо равенство
A = TB ,
где
1
A 2 ,
3
11 12 13
1
T
B 2 ,
21
22
23
31 32 33
3
пропустить 15 клеточек

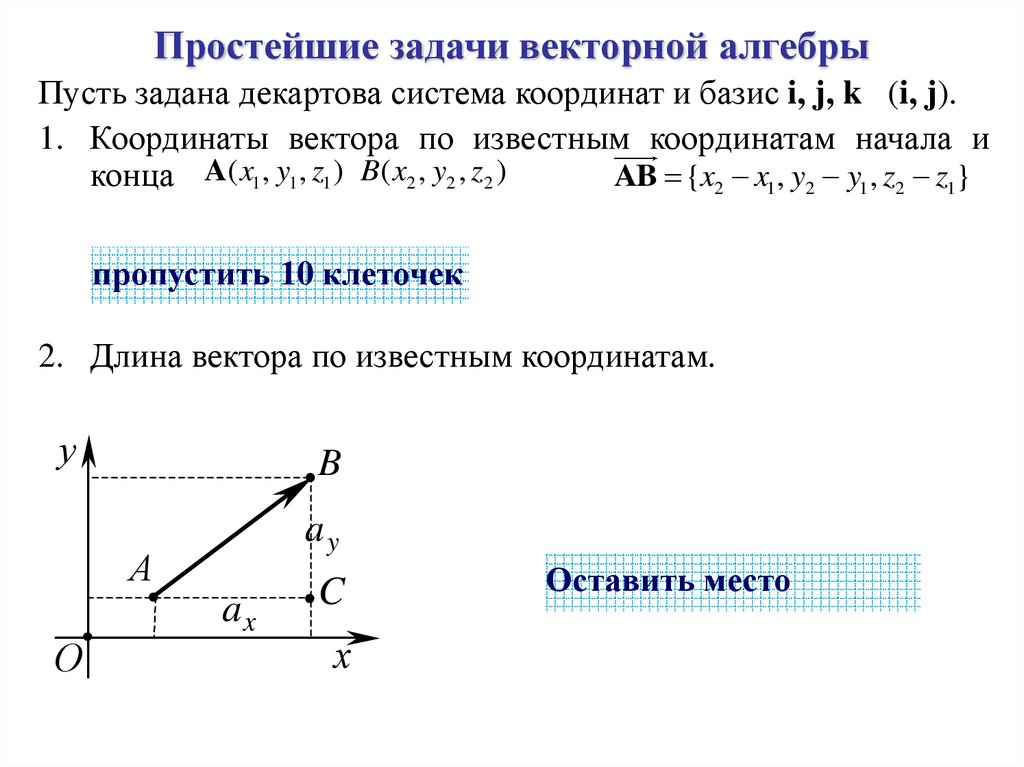
6. Простейшие задачи векторной алгебры

Пусть задана декартова система координат и базис i, j, k (i, j).
1. Координаты вектора по известным координатам начала и
конца A( x1 , y1 , z1 ) B( x2 , y2 , z2 )
AB {x2 x1 , y2 y1 , z2 z1}
пропустить 10 клеточек
2. Длина вектора по известным координатам.
y
B
ay
A
O
ax
C
x
Оставить место

7.

3. Координаты орта вектора.
ОПР. Ортом вектора ā называется вектор ā0,
сонаправленный с вектором ā и имеющий единичную длину .
Пусть , и – углы, которые вектор ā образует с координатными осями Ox , Oy и Oz соответственно .
cos , cos и cos называются направляющими косинусами
вектора ā .
пропустить 20 клеточек

8.

4. Деление отрезка в заданном соотношении.
Задача. Найти координаты точки, которая делит отрезок в
заданном отношении, если известны координаты концов
отрезка.
ОПР. Говорят, что точка M0 делит отрезок M1M2 в
отношении ( –1) если
M1M0 M0M 2
Если > 0 , то точка M0 лежит между точками M1 и M2 .
Тогда точка M0 делит отрезок M1M2 во внутреннем
отношении.
Если < 0 , то точка M0 лежит на продолжении отрезка M1M2.
Тогда точка M0 делит отрезок M1M2 во внешнем отношении.
пропустить 15 клеточек

9. Нелинейные операции на множестве векторов

1. Скалярное произведение векторов
2. Векторное произведение векторов
3. Смешанное произведение векторов
1. Скалярное произведение векторов
ОПР.
Скалярным
произведением
двух
ненулевых векторов ā и b̄ называется
число, равное произведению их модулей на
косинус угла между ними, т.е. число
(ā,b̄) = | ā | | b̄ | cos
Если ā = 0̄ или b̄ = 0̄, то скалярное
произведение векторов ā и b̄ полагают равным
Обозначают: (ā,bнулю.
̄), < ā,b̄> .

10.

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
1) (a, b ) (b , a ) (коммутативность), т.к. cos a, b cos b, a
2) ( a , b ) a Пр a b b Пр b a
ОПРЕДЕЛЕНИЕ. Проекцией вектора ā на вектор b̄ называется проекция вектора ā на ось, определяемую вектором b̄ .
пропустить 6 клеточек
3) ( a, b ) (a, b ) (a, b )
4)
(a1 a2 , b ) (a1, b ) (a2 , b )
(a, b1 b2 ) (a, b1) (a, b2 )
5) ( a , a ) a
2
6) Критерий перпендикулярности векторов. Если (a, b) 0, то a b

11.

7) Если в декартовом прямоугольном базисе векторы ā и b̄
имеют координаты: ā = {ax; ay; az} , b̄ = {bx; by; bz} , то
(ā , b̄ ) = axbx + ayby + azbz .
(1)
Формулу (1) называют выражением скалярного произведения через декартовы координаты векторов.
Почему так?
пропустить 20 клеточек
8) Если под действием постоянной силы F̄ точка перемещается
по прямой из точки M1 в M2 , то работа силы F̄ будет
равна
A F, M 1 M 2
(физический смысл скалярного произведения).