Похожие презентации:
Ферментативный катализ
1. ФЕРМЕНТАТИВНЫЙ КАТАЛИЗ
2.
1. Особенности ферментов, моделиактивного центра.
2. Основное уравнение ферментативной
кинетики. Вывод уравнения Михаэлиса –
Ментен.
3. Приемы линеаризации уравнения
Михаэлиса – Ментен.
3. ОСОБЕННОСТИ ФЕРМЕНТОВ
1. СКОРОСТЬ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ В 108 – 1020РАЗ БОЛЬШЕ, ЧЕМ СООТВЕТСТВУЮЩИХ
НЕКАТАЛИЗИРУЕМЫХ РЕАКЦИЙ.
2. СПЕЦИФИЧНОСТЬ ДЕЙСТВИЯ
3. РЕАКЦИЯ ПРОТЕКАЕТ ВНУТРИ ФЕРМЕНТ-СУБСТРАТНОГО
КОМПЛЕКСА
4.
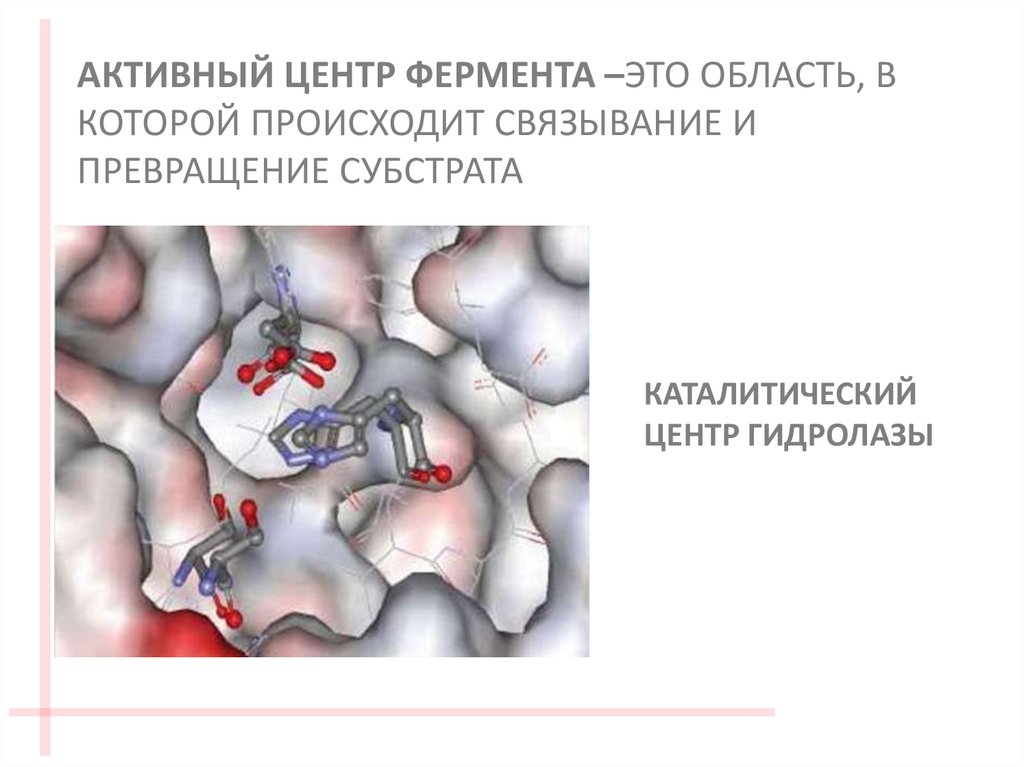
АКТИВНЫЙ ЦЕНТР ФЕРМЕНТА –ЭТО ОБЛАСТЬ, ВКОТОРОЙ ПРОИСХОДИТ СВЯЗЫВАНИЕ И
ПРЕВРАЩЕНИЕ СУБСТРАТА
КАТАЛИТИЧЕСКИЙ
ЦЕНТР ГИДРОЛАЗЫ
5.
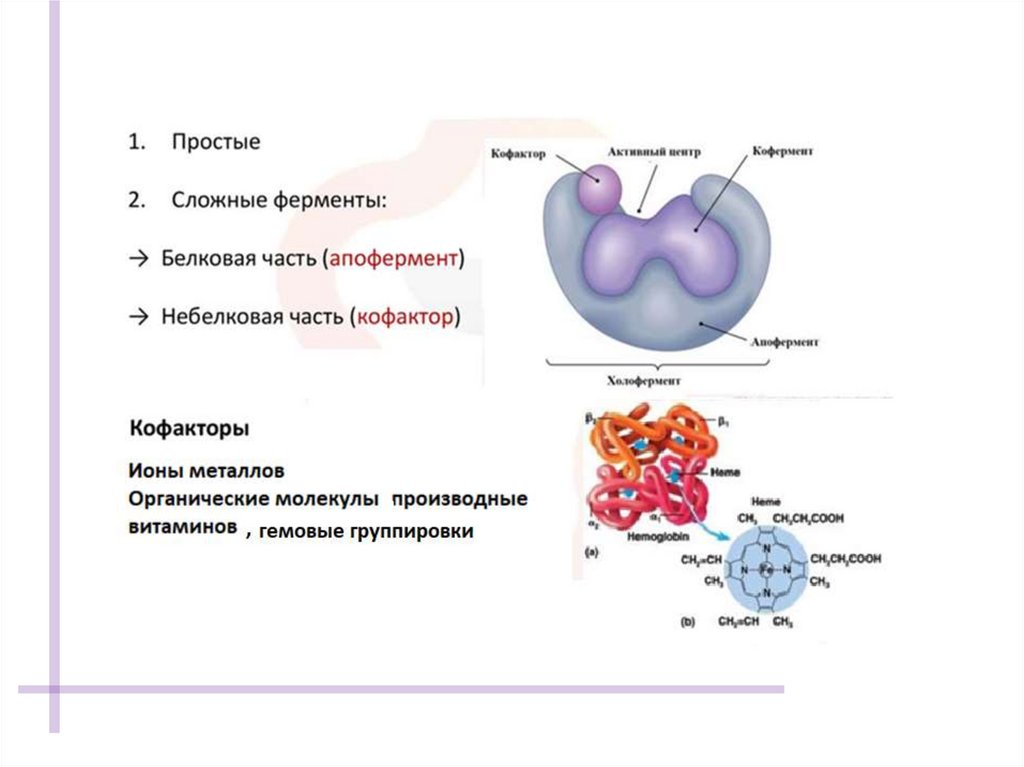
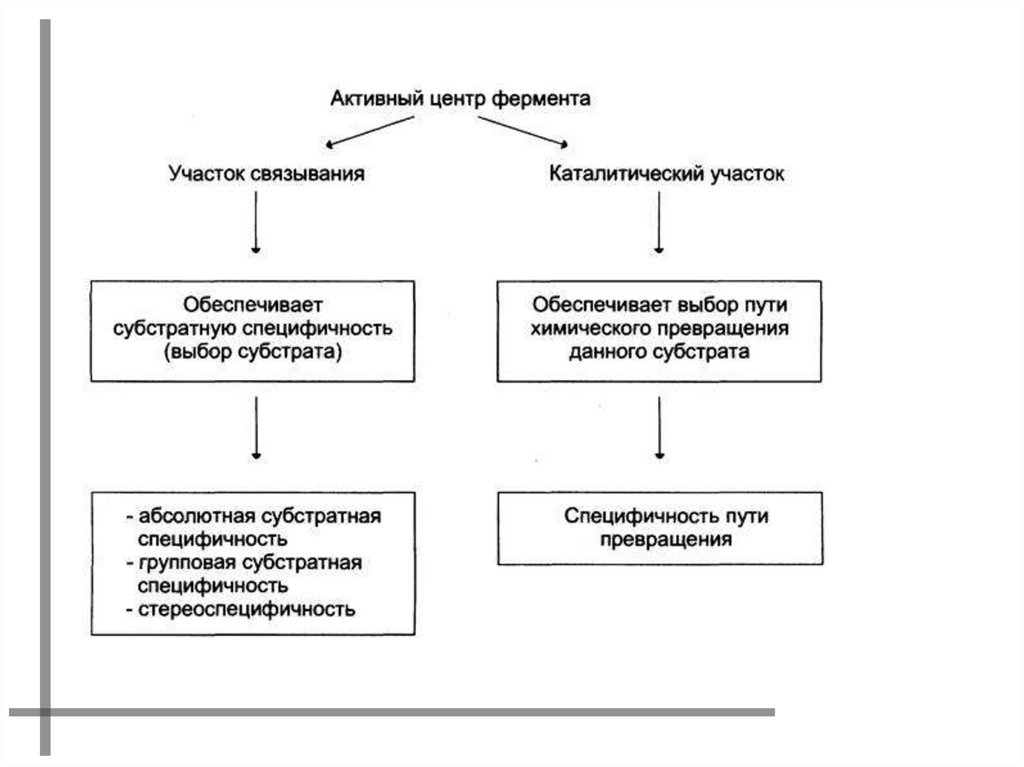
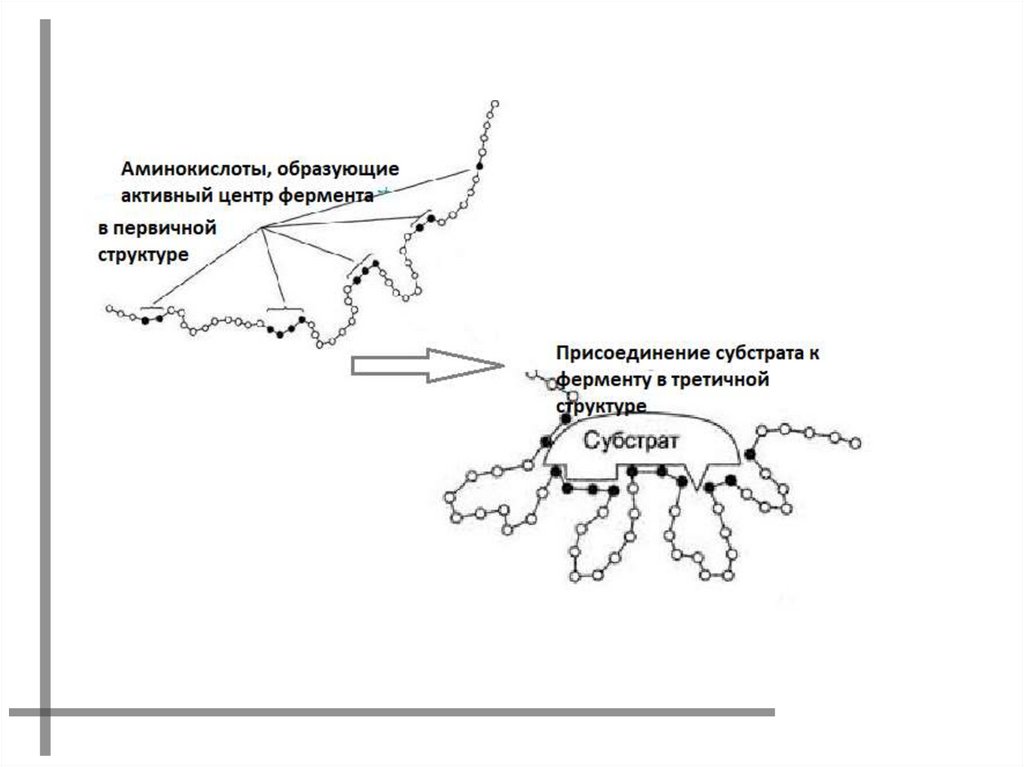
АКТИВНЫЙ ЦЕНТР ФЕРМЕНТАУчасток молекулы фермента, комплементарно
связывающийся с субстратом и обеспечивающий его
каталитическое превращение.
Формируется на уровне третичной структуры белка.
У ряда ферментов имеется кофактор (небелковый
компонент).
Участок связывания обеспечивает сродство к
субстрату и формирование фермент-субстратного
комплекса.
Каталитический участок определяет химическое
превращение субстрата.
6.
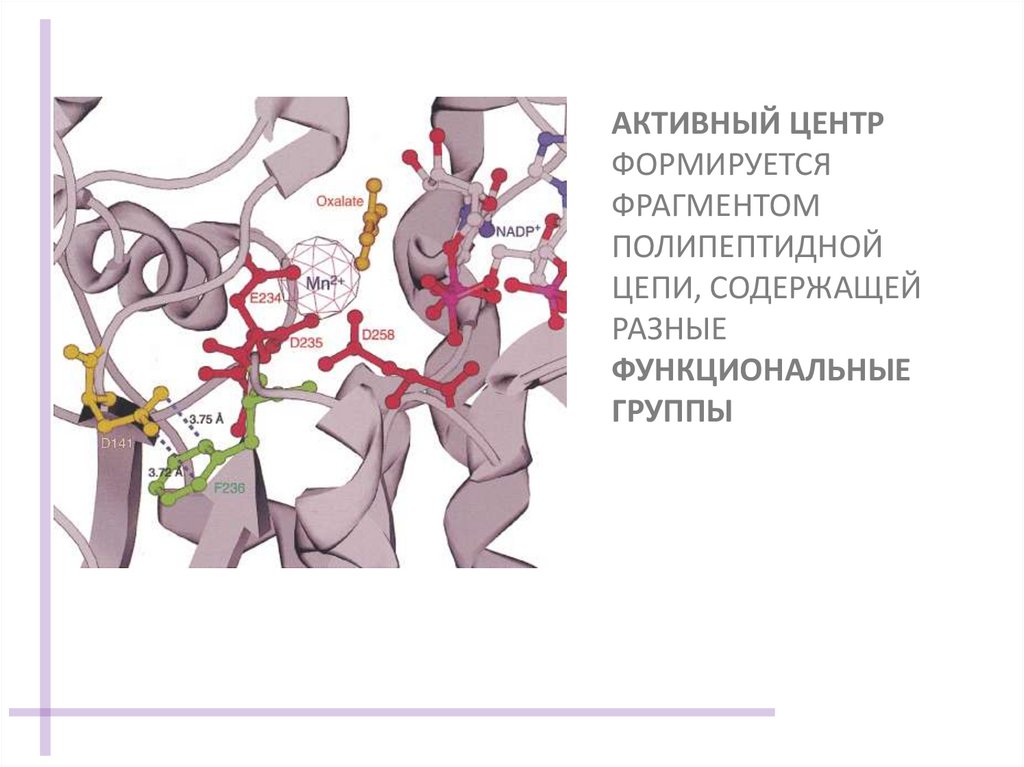
АКТИВНЫЙ ЦЕНТРФОРМИРУЕТСЯ
ФРАГМЕНТОМ
ПОЛИПЕПТИДНОЙ
ЦЕПИ, СОДЕРЖАЩЕЙ
РАЗНЫЕ
ФУНКЦИОНАЛЬНЫЕ
ГРУППЫ
7.
8.
9.
10.
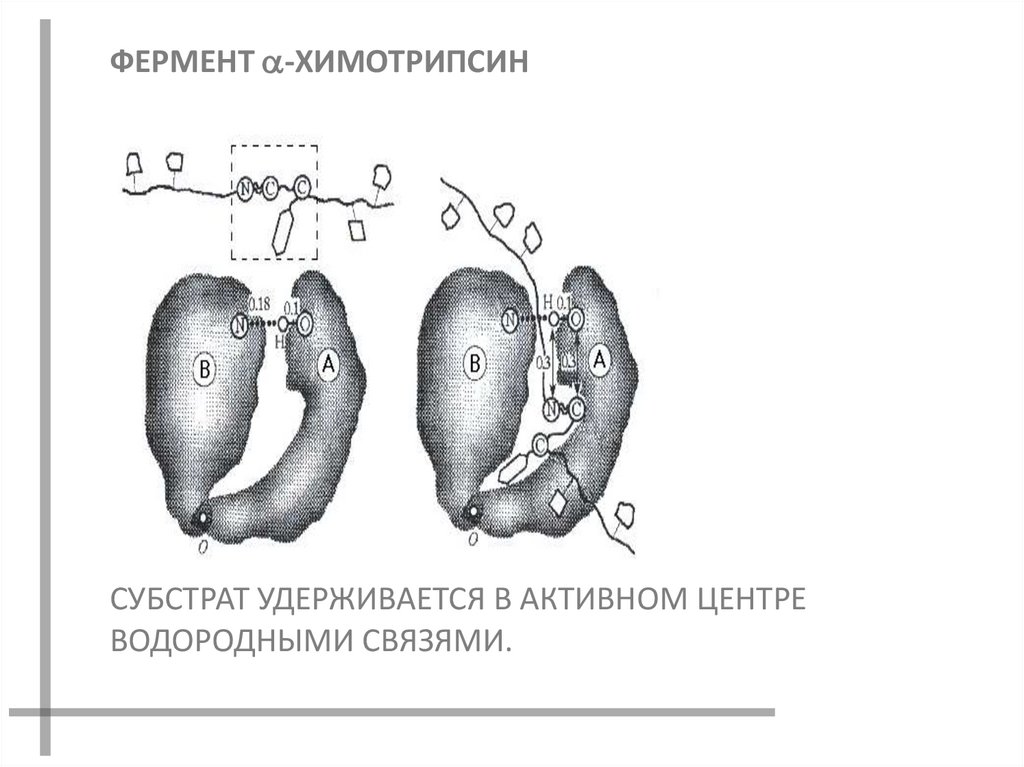
ФЕРМЕНТ -ХИМОТРИПСИНСУБСТРАТ УДЕРЖИВАЕТСЯ В АКТИВНОМ ЦЕНТРЕ
ВОДОРОДНЫМИ СВЯЗЯМИ.
11.
РОЛЬ ФУНКЦИОНАЛЬНЫХ ГРУППУЧАСТИЕ В СОРБЦИИ СУБСТРАТА
УЧАСТИЕ В ХИМИЧЕСКОМ ПРЕВРАЩЕНИИ СУБСТРАТА
12.
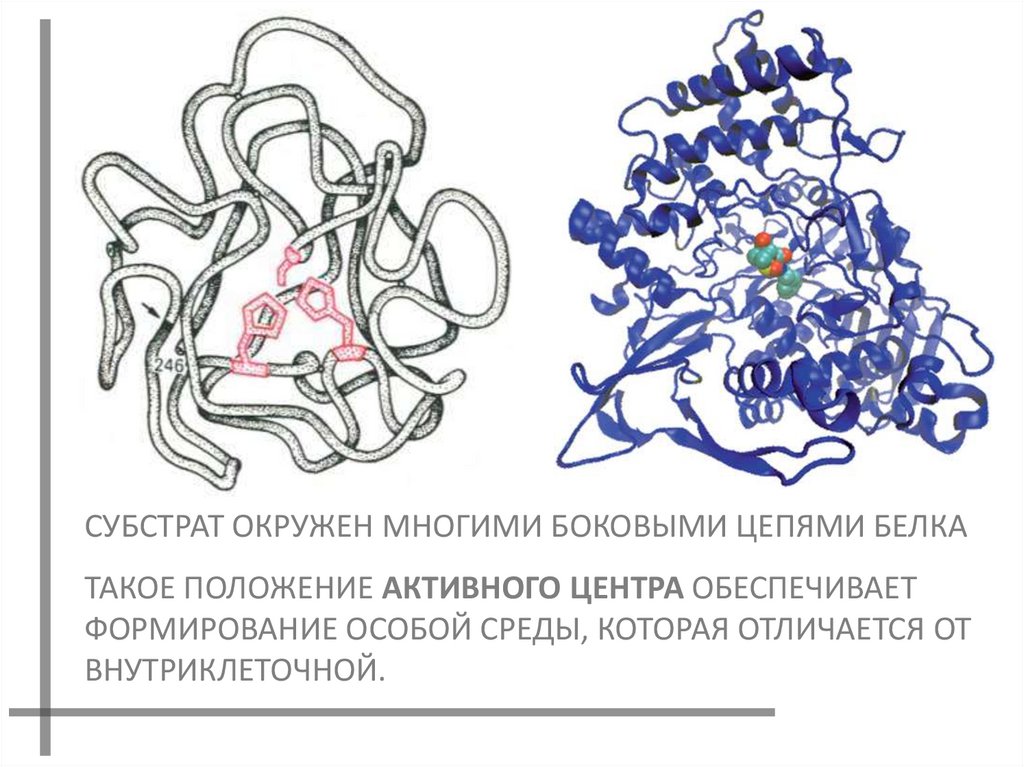
СУБСТРАТ ОКРУЖЕН МНОГИМИ БОКОВЫМИ ЦЕПЯМИ БЕЛКАТАКОЕ ПОЛОЖЕНИЕ АКТИВНОГО ЦЕНТРА ОБЕСПЕЧИВАЕТ
ФОРМИРОВАНИЕ ОСОБОЙ СРЕДЫ, КОТОРАЯ ОТЛИЧАЕТСЯ ОТ
ВНУТРИКЛЕТОЧНОЙ.
13.
Сходство ферментов с небиологическими катализаторамиферменты катализируют энергетически возможные
реакции;
энергия химической системы остаётся постоянной;
в ходе катализа направление реакции не изменяется;
ферменты не расходуются в процессе реакции.
Отличия ферментов от небиологических катализаторов
скорость ферментативных реакций выше, чем реакций,
катализируемых небелковыми катализаторами;
ферменты обладают высокой специфичностью;
ферментативная реакция проходит в клетке, т.е. при
температуре 37 °С, постоянном атмосферном давлении и
физиологическом значении рН;
скорость ферментативной реакции может регулироваться.
14. МОДЕЛИ АКТИВНОГО ЦЕНТРА ФЕРМЕНТА
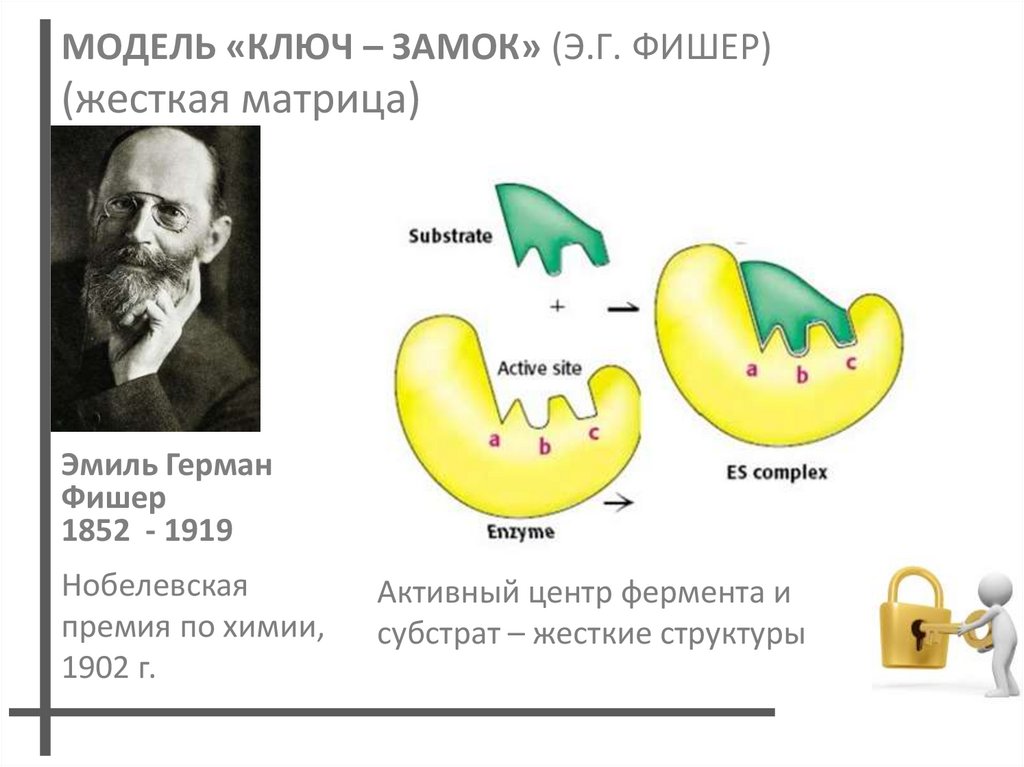
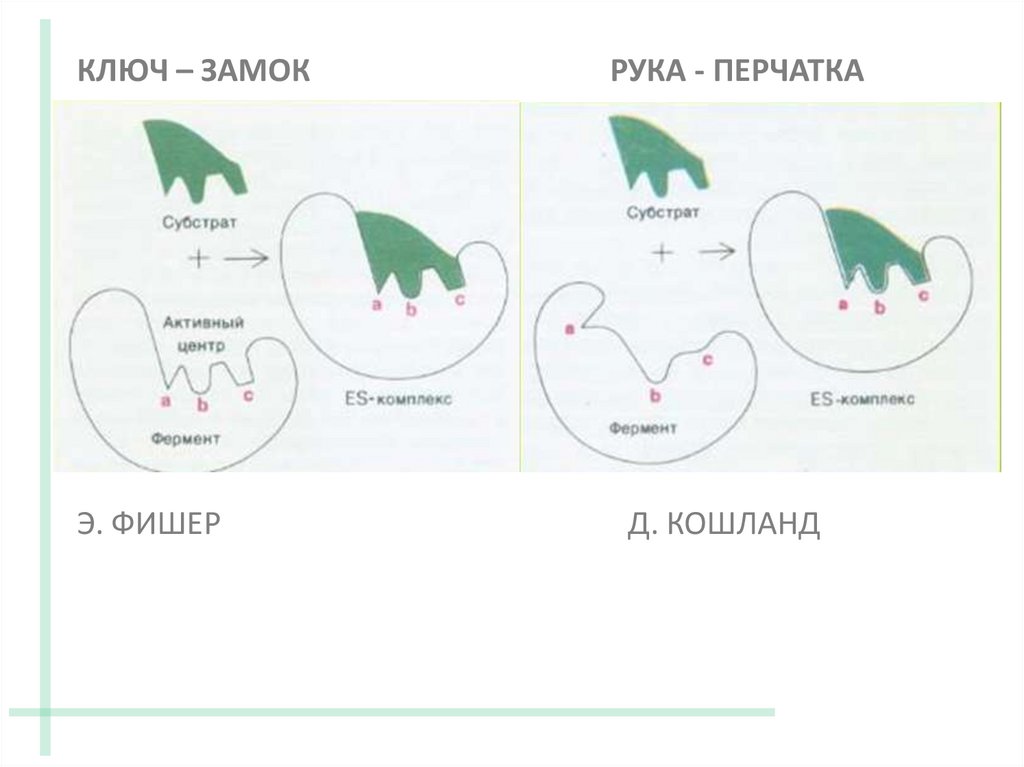
15. МОДЕЛЬ «КЛЮЧ – ЗАМОК» (Э.Г. ФИШЕР) (жесткая матрица)
Эмиль ГерманФишер
1852 - 1919
Нобелевская
премия по химии,
1902 г.
Активный центр фермента и
субстрат – жесткие структуры
16.
Модель Фишера объясняет абсолютнуюспецифичность ферментов.
Может ли такой фермент работать как катализатор?
За счет «идеального» соответствия между субстратом
и активным центром фермент-субстратный комплекс
окажется в глубоком энергетическом минимуме.
Выход из такого состояния маловероятен.
?Эта модель больше подходит для описания
ингибиторов.
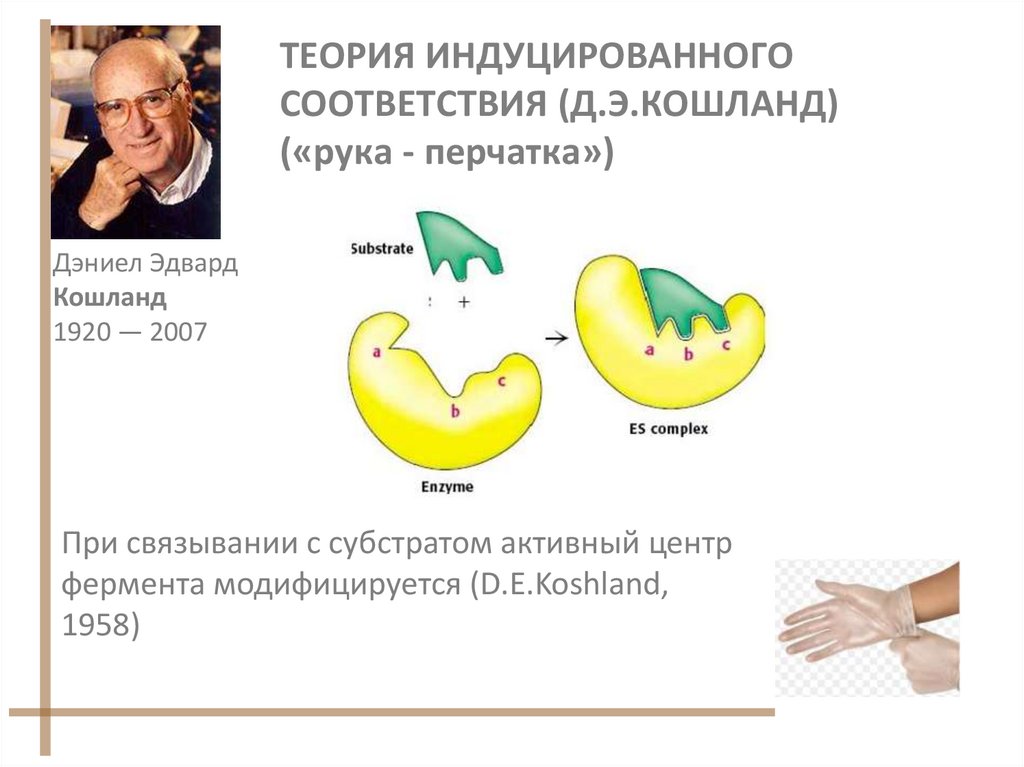
17. ТЕОРИЯ ИНДУЦИРОВАННОГО СООТВЕТСТВИЯ (Д.Э.КОШЛАНД) («рука - перчатка»)
Дэниел ЭдвардКошланд
1920 — 2007
При связывании с субстратом активный центр
фермента модифицируется (D.E.Koshland,
1958)
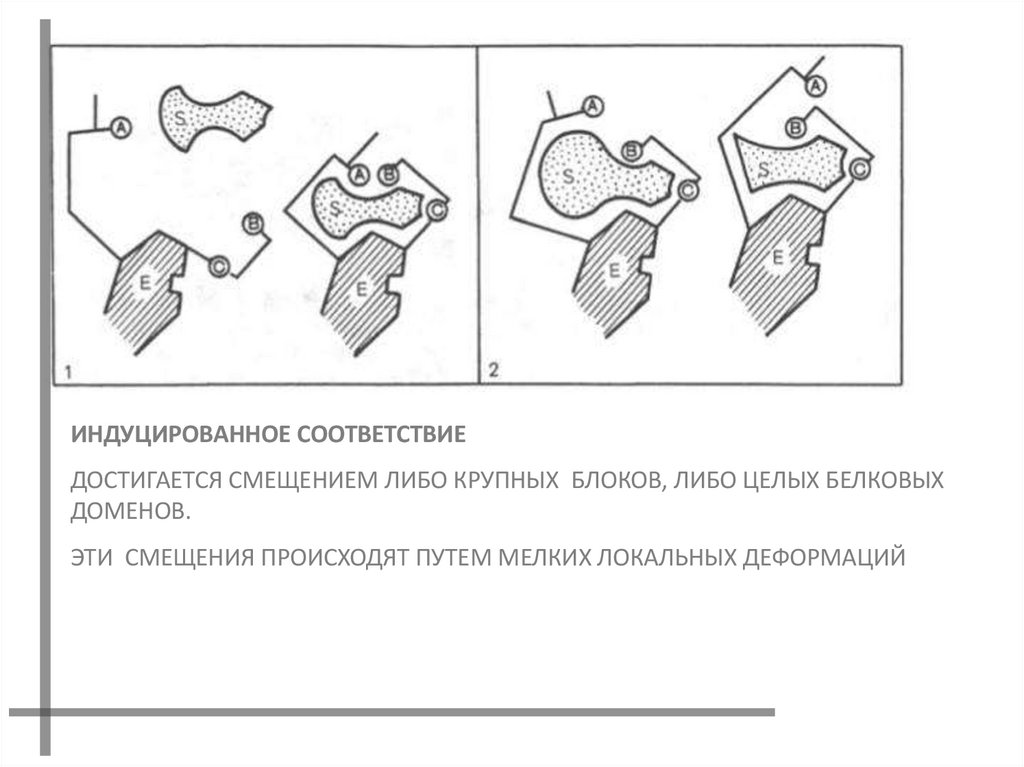
18.
ИНДУЦИРОВАННОЕ СООТВЕТСТВИЕДОСТИГАЕТСЯ СМЕЩЕНИЕМ ЛИБО КРУПНЫХ БЛОКОВ, ЛИБО ЦЕЛЫХ БЕЛКОВЫХ
ДОМЕНОВ.
ЭТИ СМЕЩЕНИЯ ПРОИСХОДЯТ ПУТЕМ МЕЛКИХ ЛОКАЛЬНЫХ ДЕФОРМАЦИЙ
19.
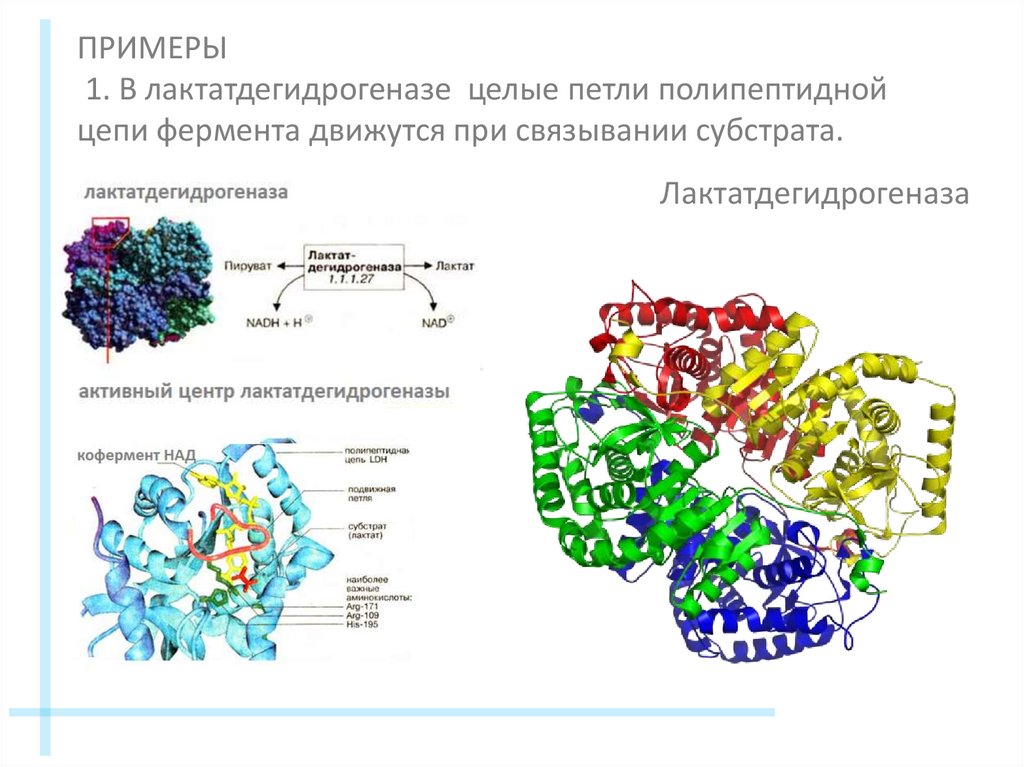
ПРИМЕРЫ1. В лактатдегидрогеназе целые петли полипептидной
цепи фермента движутся при связывании субстрата.
Лактатдегидрогеназа
20.
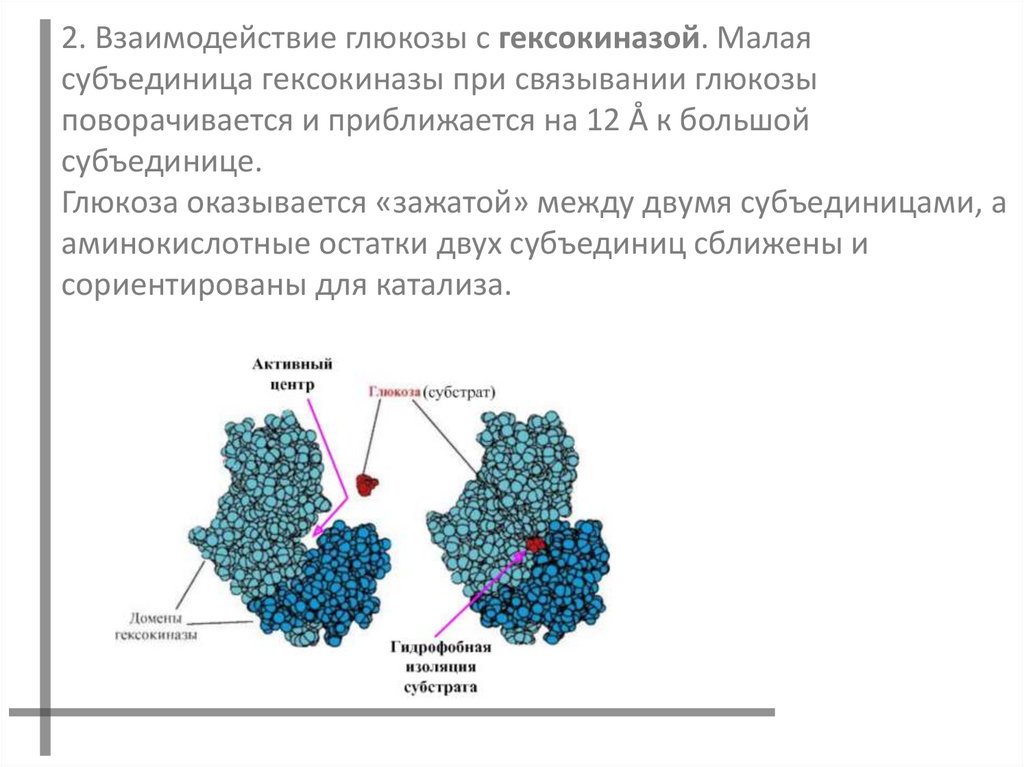
2. Взаимодействие глюкозы с гексокиназой. Малаясубъединица гексокиназы при связывании глюкозы
поворачивается и приближается на 12 Å к большой
субъединице.
Глюкоза оказывается «зажатой» между двумя субъединицами, а
аминокислотные остатки двух субъединиц сближены и
сориентированы для катализа.
21.
КЛЮЧ – ЗАМОКРУКА - ПЕРЧАТКА
Э. ФИШЕР
Д. КОШЛАНД
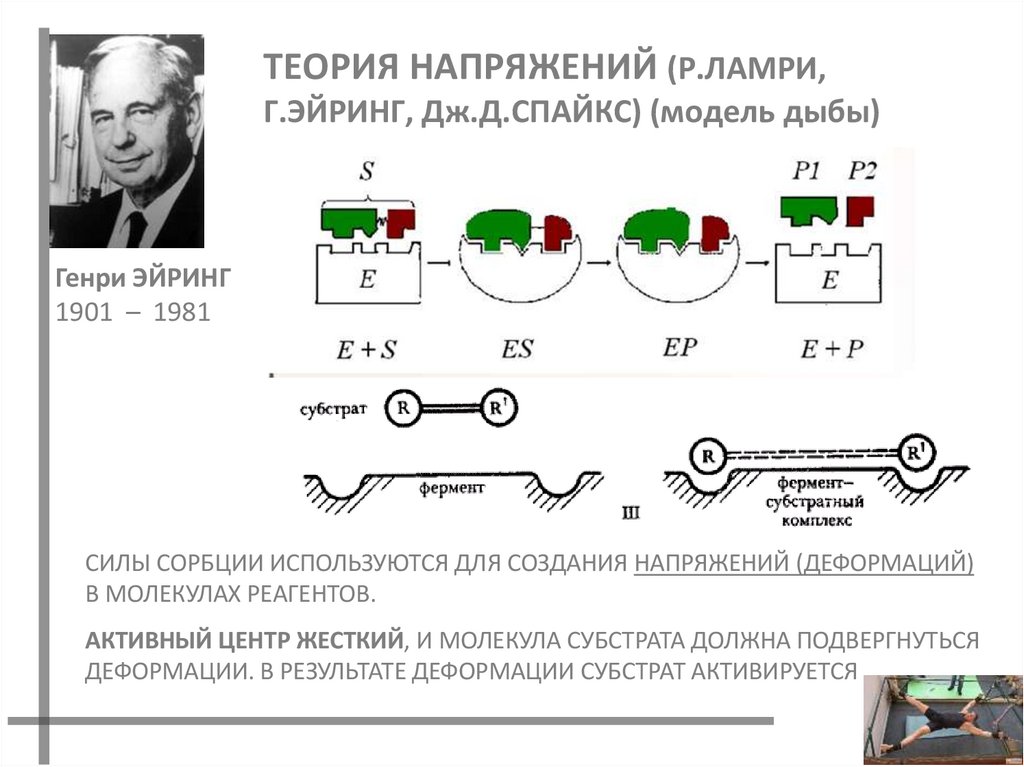
22. ТЕОРИЯ НАПРЯЖЕНИЙ (Р.ЛАМРИ, Г.ЭЙРИНГ, Дж.Д.Спайкс) (модель дыбы)
ТЕОРИЯ НАПРЯЖЕНИЙ (Р.ЛАМРИ,Г.ЭЙРИНГ, Дж.Д.СПАЙКС) (модель дыбы)
Генри ЭЙРИНГ
1901 – 1981
СИЛЫ СОРБЦИИ ИСПОЛЬЗУЮТСЯ ДЛЯ СОЗДАНИЯ НАПРЯЖЕНИЙ (ДЕФОРМАЦИЙ)
В МОЛЕКУЛАХ РЕАГЕНТОВ.
АКТИВНЫЙ ЦЕНТР ЖЕСТКИЙ, И МОЛЕКУЛА СУБСТРАТА ДОЛЖНА ПОДВЕРГНУТЬСЯ
ДЕФОРМАЦИИ. В РЕЗУЛЬТАТЕ ДЕФОРМАЦИИ СУБСТРАТ АКТИВИРУЕТСЯ
23.
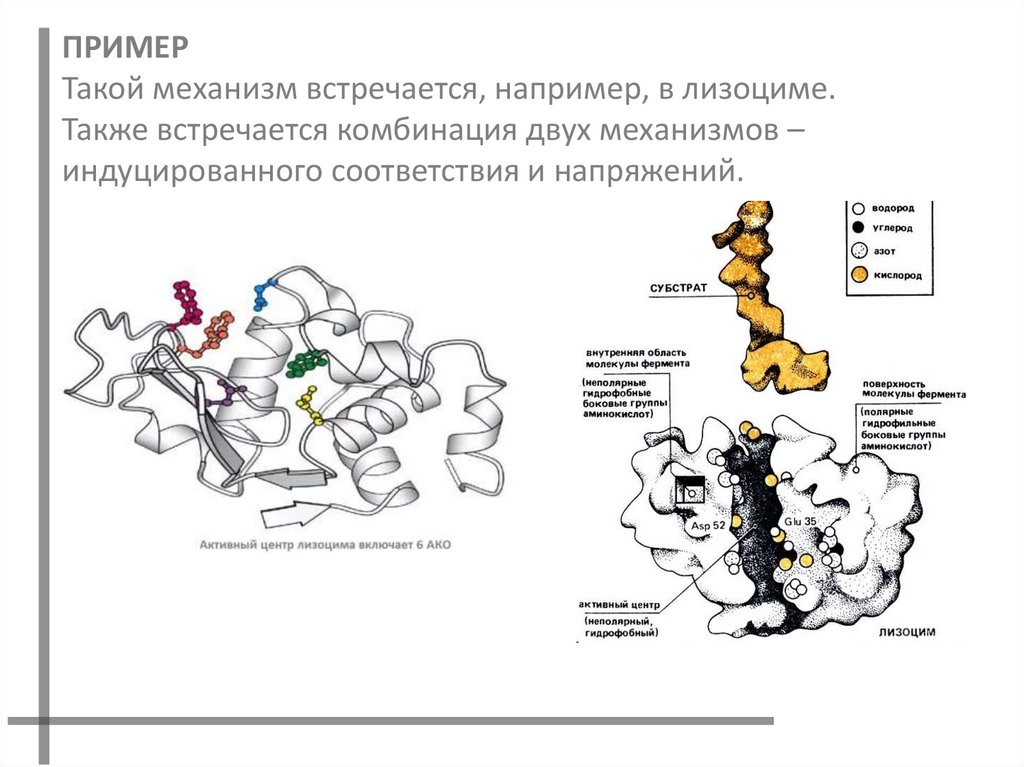
ПРИМЕРТакой механизм встречается, например, в лизоциме.
Также встречается комбинация двух механизмов –
индуцированного соответствия и напряжений.
24.
В реальных системах ни субстрат, нифермент не являются жесткими
молекулами. При связывании
претерпевают конформационные
изменения, как правило, молекулы обоих
реагентов.
Поэтому провести четкую грань между
различными механизмами катализа не
представляется возможным.
25.
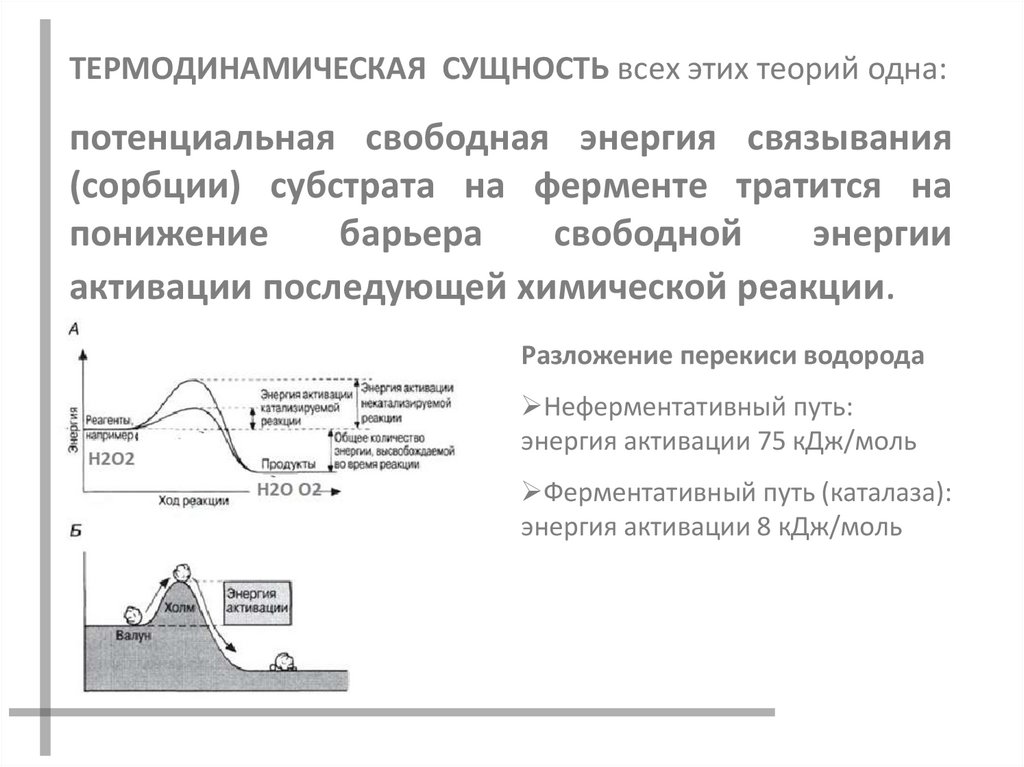
ТЕРМОДИНАМИЧЕСКАЯ СУЩНОСТЬ всех этих теорий одна:потенциальная свободная энергия связывания
(сорбции) субстрата на ферменте тратится на
понижение
барьера
свободной
энергии
активации последующей химической реакции.
Разложение перекиси водорода
Неферментативный путь:
энергия активации 75 кДж/моль
Ферментативный путь (каталаза):
энергия активации 8 кДж/моль
26.
ТИПЫ ВЗАИМОДЕЙСТВИЙ МЕЖДУ АКТИВНЫМЦЕНТРОМ ФЕРМЕНТА И СУБСТРАТОМ
В образовании фермент-субстратных комплексов
участвуют
водородные связи
электростатические взаимодействия
гидрофобные взаимодействия
ковалентные, координационные
Информация о природе связей между субстратом и
связывающим участком активного центра фермента может
быть получена методами ЭПР и ЯМР, а также методами УФ- и
ИК-спектроскопии.
27.
Прямые доказательства существования ферментсубстратного комплекса были получены в лабораторияхД. Кейлина и Б. Чанса.
В настоящее время экспериментальные и
математические методы кинетики, термодинамики и
статической механики химических реакций позволяют
определить для ряда ферментативных реакций
кинетические и термодинамические показатели, в
частности, константы диссоциации промежуточных
фермент-субстратных комплексов, константы скорости и
равновесия их образования.
28. ВЫВОД УРАВНЕНИЯ МИХАЭЛИСА – МЕНТЕН
29.
Леонор МИХАЭЛИС1875 –1949
Мод Леонора МЕНТЕН
1879 –1960
30.
Допущения:1) В стационарном состоянии скорости образования
и расходования ES равны;
2) Весь фермент в условиях насыщающих
концентраций субстрата превращается в ферментсубстратный комплекс ES
3) Если весь фермент находится в виде ES, то
скорость реакции максимальна и Vmax=k2[ES].
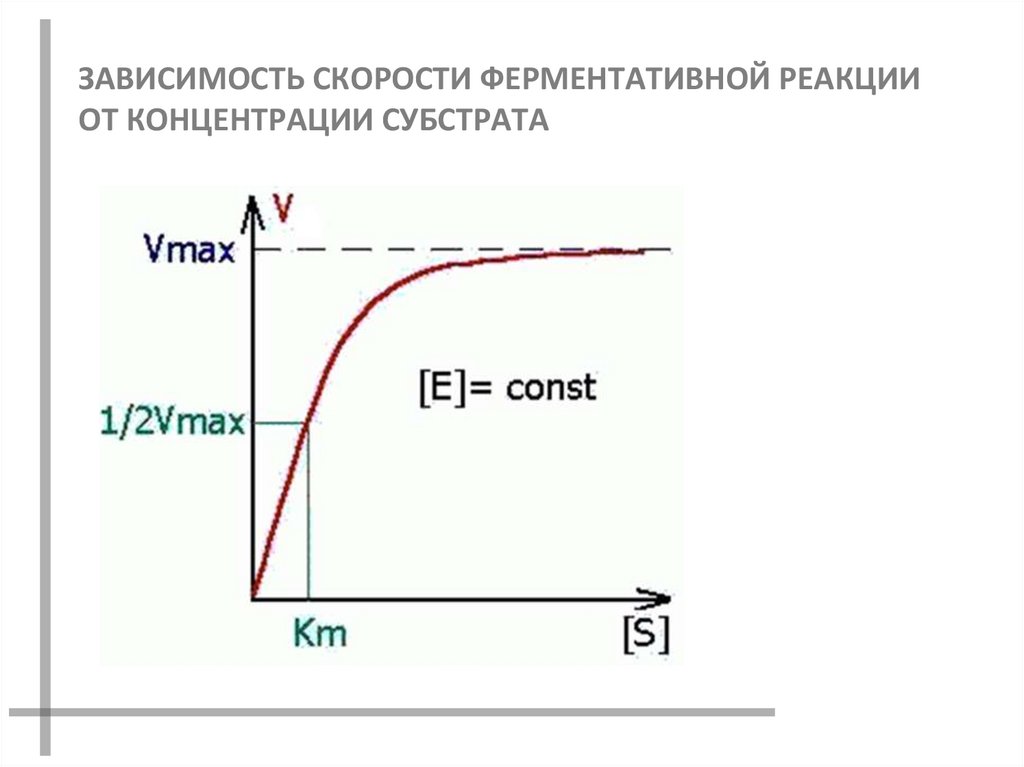
31. ЗАВИСИМОСТЬ СКОРОСТИ ФЕРМЕНТАТИВНОЙ РЕАКЦИИ ОТ КОНЦЕНТРАЦИИ СУБСТРАТА
32.
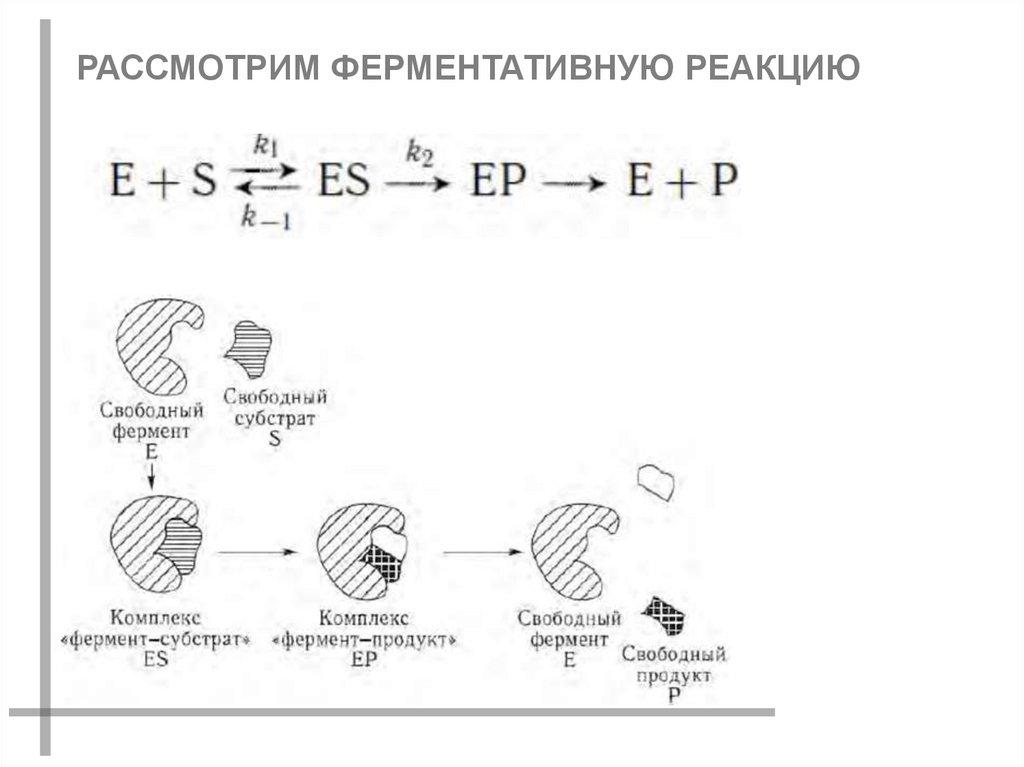
РАССМОТРИМ ФЕРМЕНТАТИВНУЮ РЕАКЦИЮ33.
ОБОЗНАЧЕНИЯ:Е1 – концентрация свободного фермента
S – концентрация субстрата
ES – концентрация фермент-субстратного комплекса
Р – концентрация продукта
34.
РАССМОТРИМ ПРИНЦИП ЗАКРЫТОСТИ СИСТЕМЫ:E E1 ES
ОТСЮДА СЛЕДУЕТ, ЧТО
E1 E ES
35.
1ОБРАЗОВАНИЯ И
V1 СКОРОСТЬ
РАСЩЕПЛЕНИЯ ФЕРМЕНТ-
СУБСТРАТНОГО КОМПЛЕКСА
d ES
V1
k1 E1 S k 1 k2 ES
dt
36.
В СТАЦИОНАРНОМ СОСТОЯНИИ V1 =0, ТОГДАk1 E1 S k 1 k2 ES 0
УЧТЕМ ПРИНЦИП ЗАКРЫТОСТИ СИСТЕМЫ
E1 E ES
37.
k1 ( E [ ES ]) S k 1 k2 ES 0Раскроем скобки и выразим [ES]
38.
ESE S
k 1 k 2
k1
S
39.
ОТНОШЕНИЯ КОНСТАНТ СКОРОСТЕЙ ЗАМЕНИМ КМk 1 k 2
KM
k1
ТОГДА
E S
ES
K M S
40.
1ЗАПИШЕМ СКОРОСТЬ ФЕРМЕНТАТИВНОЙ РЕАКЦИИ
КАК СКОРОСТЬ ОБРАЗОВАНИЯ ПРОДУКТА
d P
V
k 2 ES
dt
ПОДСТАВИМ ВЫРАЖЕНИЕ ДЛЯ
ES
41.
ПОЛУЧИМd P
E S
V
k 2 ES k 2
dt
K M S
42.
УЧТЕМ, ЧТОVmax k 2 E
В ЭТОЙ СИТУАЦИИ ВЕСЬ ФЕРМЕНТ ПОТРАЧЕН НА
ОБРАЗОВАНИЕ ФЕРМЕНТ-СУБСТРАТНОГО
КОМПЛЕКСА.
43.
В ИТОГЕ ПОЛУЧИМ УРАВНЕНИЕ МИХАЭЛИСА –МЕНТЕН
Vmax S
V
K M S
44.
Константа Михаэлисаизмеряется в молях на литр и
колеблется от 10-2 до 10-7
моль/л.
Чем меньше КМ, тем активнее
фермент.
При V=1/2Vmax, имеем КМ = [S].
Однако определение Vmax и КМ
затруднительно.
Для определения КМ и Vmax
используют прием линеаризации
уравнения Михаэлиса – Ментен.
45. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЯ МИХАЭЛИСА – МЕНТЕН
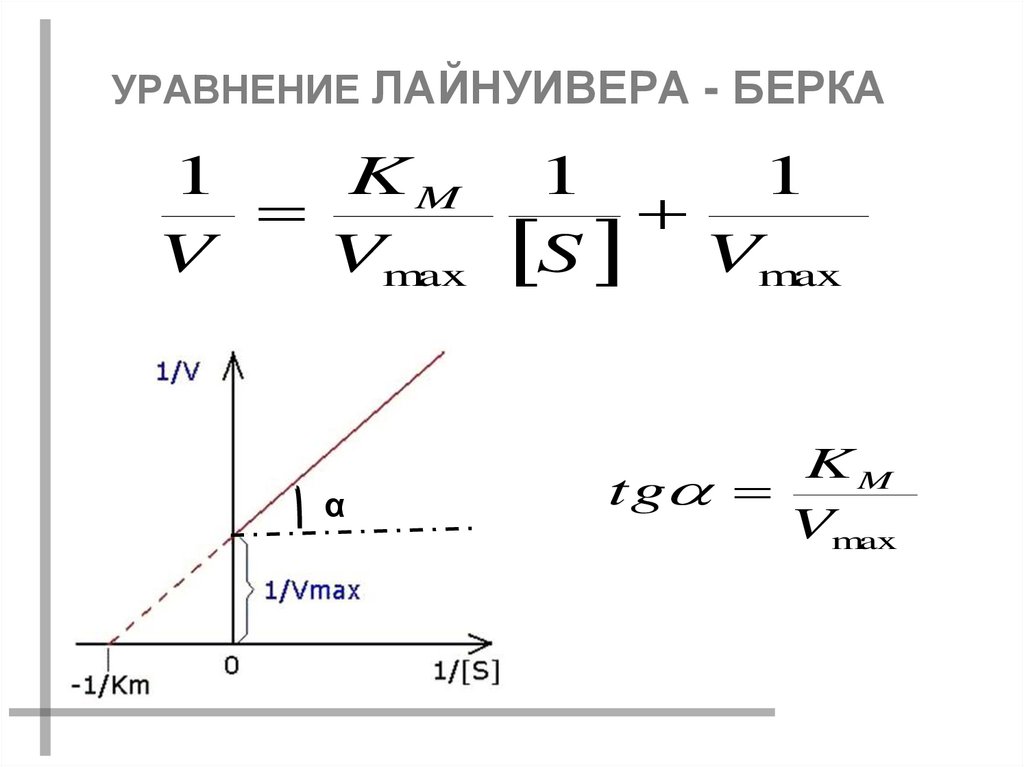
46. УРАВНЕНИЕ ЛАЙНУИВЕРА - БЕРКА
1KM
V
Vmax
α
1
1
S Vmax
KM
tg
Vmax
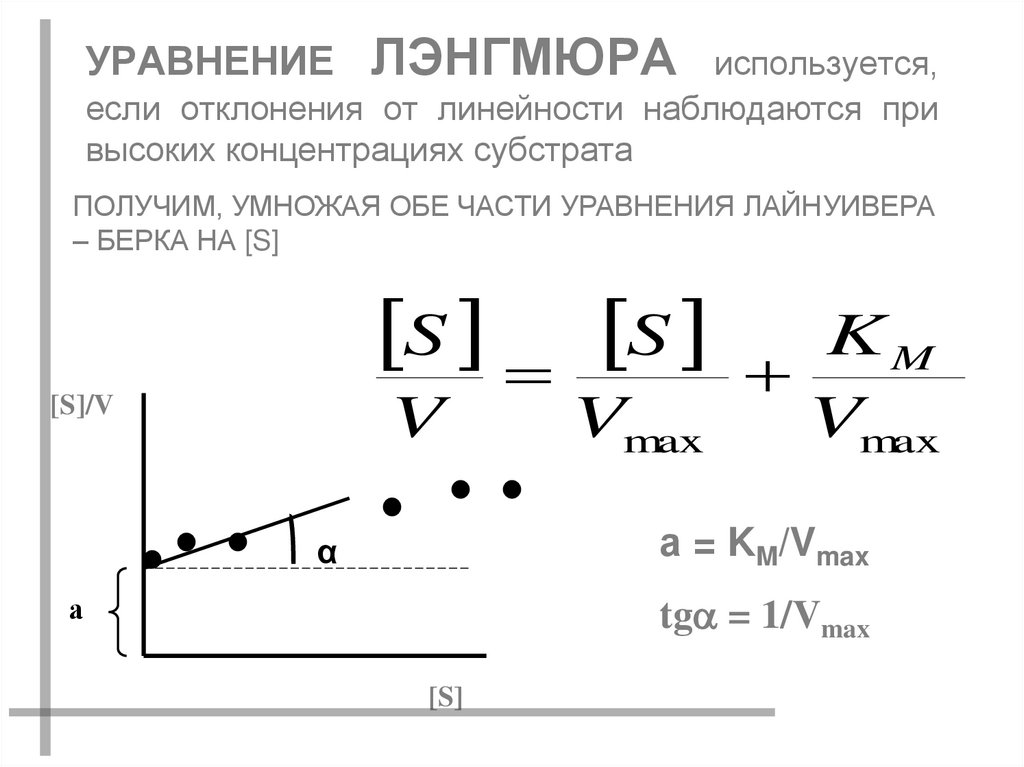
47. УРАВНЕНИЕ ЛЭНГМЮРА используется, если отклонения от линейности наблюдаются при высоких концентрациях субстрата
ПОЛУЧИМ, УМНОЖАЯ ОБЕ ЧАСТИ УРАВНЕНИЯ ЛАЙНУИВЕРА– БЕРКА НА [S]
S S K M
[S]/V
V
Vmax
Vmax
а = KM/Vmax
α
а
tg = 1/Vmax
[S]
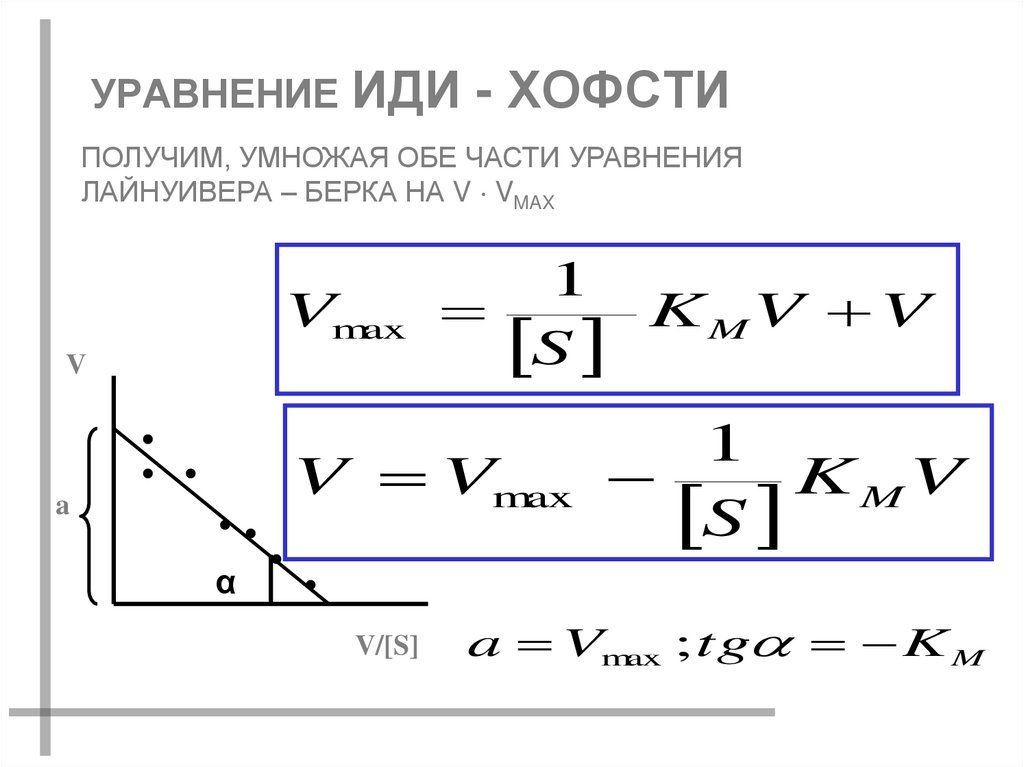
48. УРАВНЕНИЕ ИДИ - ХОФСТИ
ПОЛУЧИМ, УМНОЖАЯ ОБЕ ЧАСТИ УРАВНЕНИЯЛАЙНУИВЕРА – БЕРКА НА V VMAX
1
Vmax
K MV V
S
V
1
V Vmax
K MV
S
a
α
V/[S]
a Vmax ; tg K M



















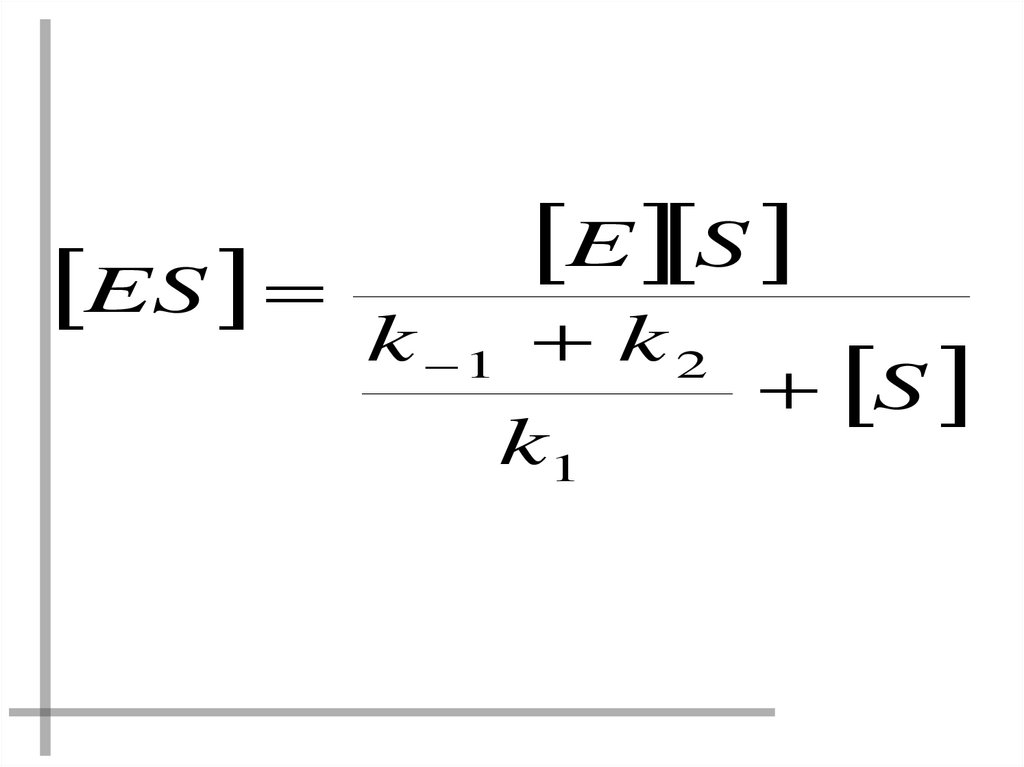


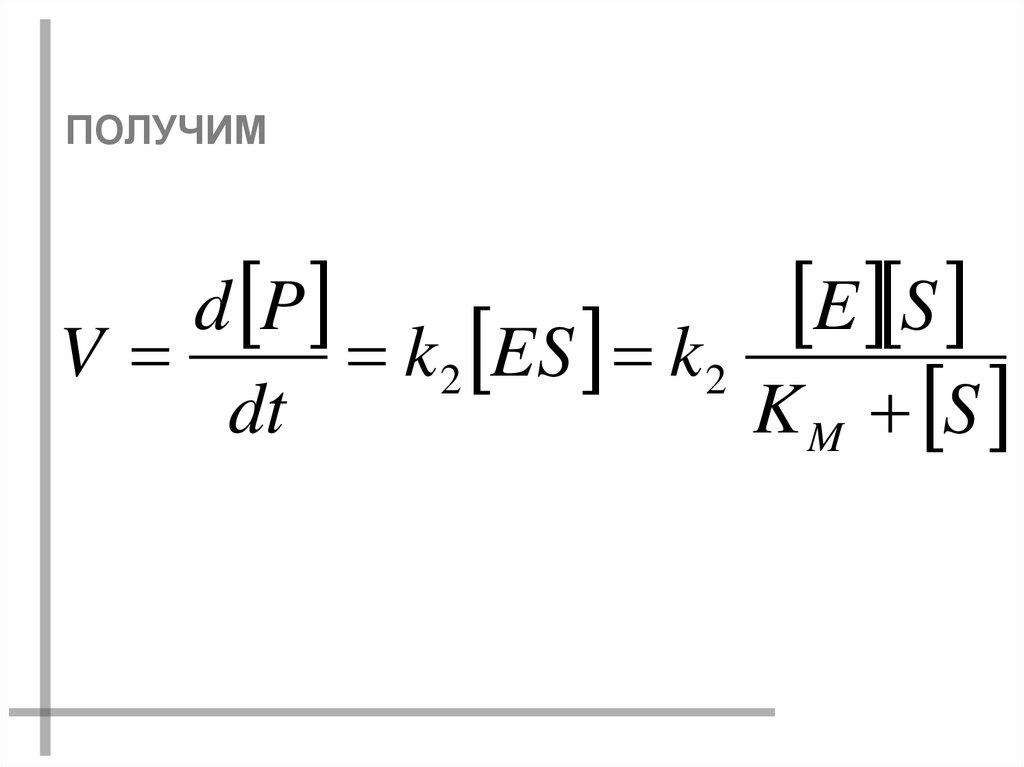

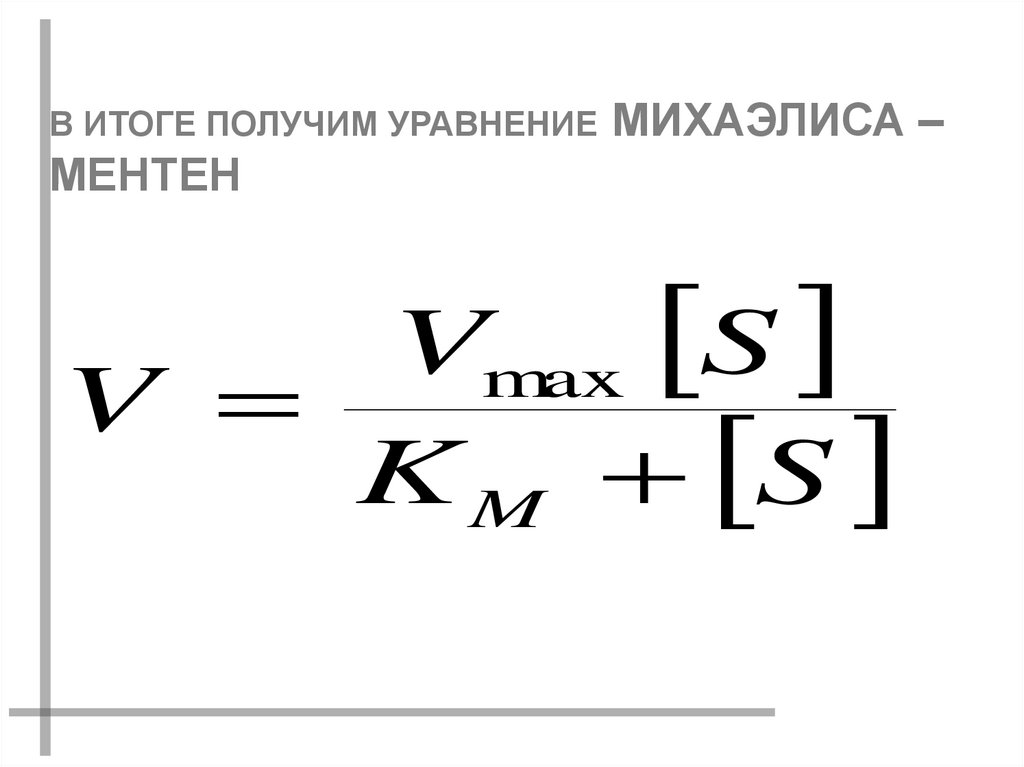


 Биология
Биология








