ГЂ†Ґ†3-з†бвм1

1. Курс «Математическое моделирование процессов в природных, социально-экономических средах»

КУРС
«МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ПРОЦЕССОВ В ПРИРОДНЫХ,
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ СРЕДАХ»

2. Глава 3 МЕТОДЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

ГЛАВА 3
МЕТОДЫ ПОСТРОЕНИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
Часть 1
2

3.

1.Построение математических моделей
на основе законов сохранения
При построении математической модели изучаемого объекта из
всех
характеризующих
его
связей
выделяются
наиболее
существенные. Эти связи, как правило, записываются в виде
уравнений,
которые
естествознания.
Сами
выражают
объекты
фундаментальные
могут
быть
законы
совершенно
различными по своей природе и назначению физические или
биологические явления, технологические процессы, механизмы
или конструкции. Остановимся на методологии построения
математических моделей явлений и процессов, основанной на
законах сохранения.
3

4.

Пусть величина является количественной характеристикой
некоторого свойства элемента исследуемой системы (массы,
импульса, энергии и т. п.). Вообще говоря,
компонентами
xi ( i 1, n )
вектор с
k ( k 1, s ). Через вектор х с компонентами
обозначим
индивидуальные
признаки
элемента
системы (например, координаты, фазовые переменные), а через t
независимую переменную, характеризующую время. Основные
характеристики
являются
функциями
индивидуальных признаков, т. е. = ( t, х).
времени
и
4

5.

В
точных
науках
(в
физике,
механике
и
астрономии)
существовала тенденция формулировки своих законов в форме
F( ) = const
описывающей
зависимость
системы.
этом
При
между
константа
(1)
свойствами
справа
элементов
сохраняется
вдоль
траектории движения элемента в пространстве Rn. Зависимости
(1) называют законами сохранения.
5

6.

Зависимости вида (1) справедливы при вполне определенных
условиях.
Например, закон Бойля-Мариотта
pV = const
(р давление, V объем данной массы газа) справедлив при
постоянной температуре Т.
Уравнение состояния Клайперона
p = RT
( и R соответственно плотность газа и газовая постоянная)
справедливо для идеального разреженного газа.
6

7.

Уравнение состояния Ван-дер-Ваальса
(р + a 2)( 1 – 4cg) = RT
(в котором cg параметр Ван-дер-Ваальса, учитывающий долю
газового объема, приходящегося на собственный объем молекул,
множитель
а
вычисляется
межмолекулярного
по
параметрам
взаимодействия
или
по
потенциала
параметрам
критического состояния газа) оправдано, строго говоря, в
области
сравнительно
высоких
температур
и
умеренных
давлений.
Постоянство суммы кинетической и потенциальной энергий
выполняется для консервативных (гамильтоновых) систем.
7

8.

Стремление исследователей расширить область применения
законов сохранения приводит к необходимости выяснения
причин изменения соответствующих констант. Если такие
причины, часто именуемые воздействиями, выявлены с нужной
степенью точности, то это удается сделать.
Пусть для определенности рассматривается дискретная система,
а k(t, х) это количественные характеристики различных
свойств элементов системы. Тогда для системы можно ввести
признак
k ( t , x)
(2)
k
(вообще говоря, векторное свойство). В этом случае свойства и
индивидуальные признаки связаны с элементами системы.
8

9.

Если имеем дело со сплошной средой (континуумом), то вместо k
вводится плотность признака . Это позволяет вместо (2)
воспользоваться интегральной характеристикой
( t , x )d .
(3)
Здесь область задания вектора х индивидуальных признаков.
В случае континуума его свойства и индивидуальные признаки
связаны с физически бесконечно малым объемом среды.
9

10.

Если F известное воздействие (векторное, вообще говоря), то в
любом из указанных случаев (для дискретной системы и
континуума) удается записать выражение
d
F.
dt
(4)
Это выражение в случае континуума или интеграл от него по
времени часто называют интегральной формой закона сохранения.
10

11.

Воздействие F можно представить в форме
F = F+ F ,
где F+ характеризует количественный рост признака Ф, a
F
его убыль. При этом данное воздействие может быть функцией
параметров k (для дискретной системы) или плотности (для
континуума), дифференциальным оператором, функционалом. От
этого
зависит
характер
уравнения
(4)
(обыкновенное
дифференциальное уравнение, дифференциальное уравнение в
частных
производных,
интегродифференциальное
и т. д.), а также степень его сложности.
уравнение
11

12.

Дальнейшее обобщение понятия закон сохранения заключается в
том,
что
под
ним
подразумевается
схема
рассуждения,
позволяющая установить связь между самими признаками или
признаками и воздействиями, а не конкретный математический
аппарат
описания
явления
или
процесса.
Если
же
последовательность рассуждений удается записать в виде (4), то
будем считать, что сформулирован закон сохранения (дана его
12
математическая формулировка).

13.

В математическом моделировании наиболее распространен метод
от общего к частному: здесь для создания математических
моделей применяют фундаментальные законы природы. Это могут
быть:
законы
сохранения,
которым
удовлетворяет
рассматриваемый объект, эволюционные законы природы, которым
подчиняются эти явления; вариационные принципы общие
утверждения о движении (эволюции) объекта, подчиняющиеся
13
определенным экстремальным условиям.

14.

Законов сохранения в природе достаточно много, в физике это
законы
сохранения
массы,
энергии,
импульса,
моментов
для
построения
анализа
реального
импульса, числа частиц, заряда и т.д.
Использование
законов
математических
моделей
сохранения
начинается
с
процесса. Закон, присущий данному объекту, записывается в
математических терминах.
14

15.

Чаще всего первоначальная модель является достаточно простой
и может быть сведена к обыкновенному дифференциальному
уравнению. Затем проводится исследование поведения модели,
результаты сравнивают с данными эксперимента или расчетами
на основе других моделей, т.е. выясняют адекватность модели
изучаемому явлению.
15

16.

Закон сохранения импульса: полный импульс замкнутой
системы частиц не изменяется со временем
p pi mi vi const.
i
i
Закон сохранения импульса связан с однородностью пространства
(инвариантность относительно пространственных сдвигов).
16

17.

Закон сохранения момента импульса: момент импульса
любой системы частиц, в которой суммарный момент внешних
сил равен нулю, сохраняется со временем.
Ls ( rsi pi ) const,
i
где
Ls
момент импульса системы относительно центра
инерции s.
Закон сохранения момента импульса связан с изотропностью
пространства
пространства).
(инвариантность
относительно
вращений
17

18.

Закон
сохранения
механической
энергии:
полная
механическая энергия замкнутой системы n частиц, в которой
нет диссипативных сил, сохраняется в процессе движения.
ma va2
E
U ( r1 , r2 ,..., rn ) const.
2
a
18

19.

Первое слагаемое в (5) – кинетическая
инерциальной
системе
отсчета
в
энергия Т. В
декартовых
координатах
кинетическая энергия есть квадратичная форма скоростей.
Функция U – потенциальная энергия, в силу однородности
пространства она может зависеть не от всех N радиус-векторов
ri ( i 1, N )
частиц, но только от их (N – 1) независимых
разностей
ra rb .
19

20.

Сохранение
энергии
связано
с
однородностью
времени
(инвариантность физических законов относительно изменения
начала отсчета).
20

21.

Теорема об изменении кинетической энергии:
Изменение кинетической энергии Т системы равно работе А,
которую совершают все силы, действующие на все частицы
системы.
Т2 – Т1 = А.
21

22.

Закон сохранения вещества (массы): сумма масс веществ до
реакции равна сумме масс веществ после реакции.
Отметим, что в релятивистской физике есть более точный закон
сохранения массы – энергии.
E
Всякая энергия Е обладает массой m 2 , где с – скорость света
c
в вакууме.
22

23.

Закон
сохранения
электрических
зарядов
заряда:
любой
алгебраическая
замкнутой
сумма
(электрически
изолированной) системы остается неизменной, какие бы процессы
ни происходили внутри этой системы.
23

24.

Первое начало термодинамики.
Если состояние системы изменяется вследствие подвода к ней
некоторого количества тепла dQ и при этом изменении состояния
система совершает работу dA, то закон сохранения энергии гласит:
количество подведенного тепла равно сумме произведенной
работы и изменения внутренней энергии системы dU:
dQ = dU + dA.
24

25.

Математическая модель объекта чаще всего представляет собой
обыкновенное дифференциальное уравнение или в частных
производных,
или
систему
дифференциальных,
интегро-
дифференциальных уравнений, описывающих реальный процесс
(явление).
Рассмотрим несколько примеров построения математических
моделей на основе законов сохранения.
25

26.

1.1.
Движение шарика, присоединенного к пружине
(закон сохранения энергии)
В получении моделей механических динамических систем главную
роль
играют
фундаментальные
законы,
определяющие
происхождение и величину сил, действующих на объект, а второй
закон Ньютона может быть
как бы вспомогательным и
применяться на последней стадии построения модели. Конечно же,
такое деление чисто условно.
26

27.

Ведь если речь идет о задачах динамики, то можно использовать
и другую схему сначала связать с помощью закона Ньютона
проекции ускорения тела с проекциями действующих на него
сил, а затем, исходя из тех или иных соображений, вычислить
эти силы как функции координат, получив замкнутую модель.
27

28.

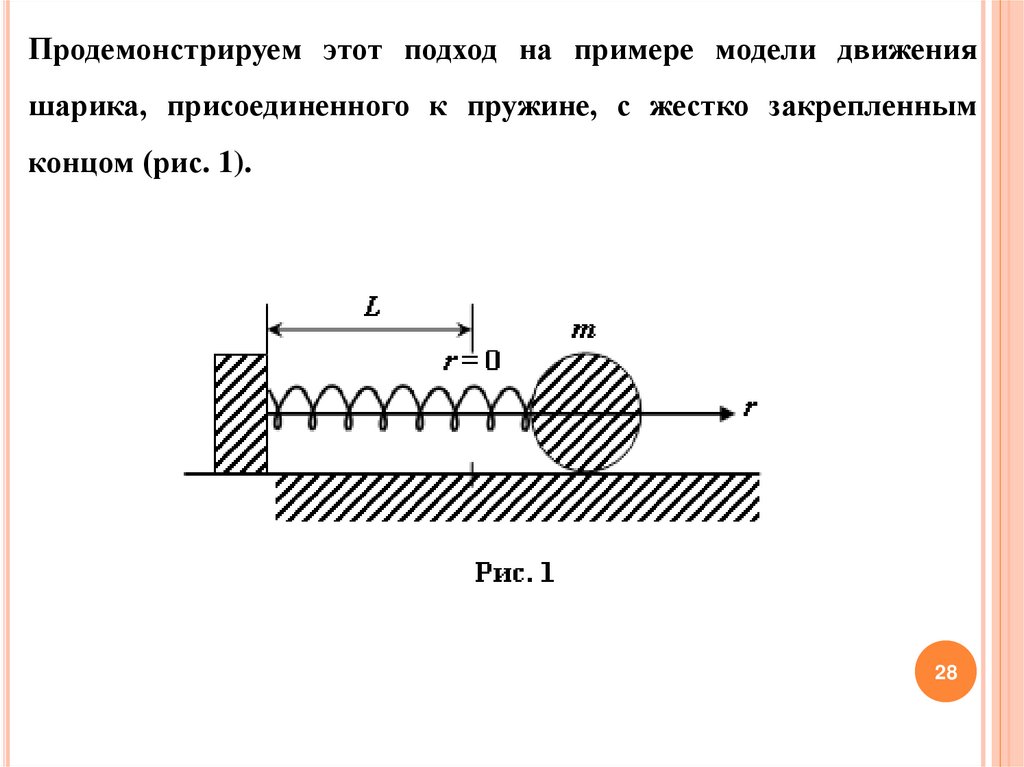
Продемонстрируем этот подход на примере модели движения
шарика, присоединенного к пружине, с жестко закрепленным
концом (рис. 1).
28

29.

1 способ (2 закон Ньютона)
Пусть r координата шарика вдоль оси пружины, лежащей на
горизонтальной плоскости, и направление движения шарика
совпадает с ее осью. Тогда по второму закону динамики
F ma m
d 2r
dt 2
где т масса шарика, а его ускорение. Будем считать плоскость
идеально гладкой (т. е. движение происходит без трения),
пренебрежем также сопротивлением воздуха и примем во
внимание то, что вес шарика уравновешивается реакцией
плоскости. Единственная сила, действующая на шарик в
направлении оси r, очевидно, сила упругости пружины.
29

30.

Определим ее, используя закон Гука, гласящий, что для
растяжения (сжатия) пружины необходимо приложить силу
F = kr,
где коэффициент k > 0 характеризует упругие свойства пружины,
а r величину ее растяжения или сжатия относительно
нейтрального, ненагруженного положения r = 0. Уравнение
движения шарика принимает вид (уравнение элементарного
осциллятора)
m
d 2r
dt 2
kr ,
t 0.
(1)
30

31.

Оно описывает его гармонические колебания и имеет общее
решение
r = Asin t + Bcos t,
где
k/m
(2)
собственная частота колебаний системы
«пружина-шарик». Значения А и В легко определяются из
начального состояния объекта, т. е. через величины r(t = 0) = r0 и
v(t = 0) = v0 (v(t) скорость шарика), причем r(t) 0 при r0 = v0 = 0.
31

32.

2 способ (закон сохранения энергии)
Подходы, с помощью которых создаются модели не должны,
разумеется, противоречить другим фундаментальным законам
природы. Соответствующая проверка непротиворечивости (если
она возможна) весьма полезна для установления корректности
моделей. Поясним это, используя для вывода уравнения (1) не
закон Ньютона, а закон сохранения энергии.
32

33.

Поскольку точка крепления пружины неподвижна, то стенка не
совершает работу над системой «пружина-шарик» (и наоборот), и
ее
полная
механическая
энергия
Е
остается
постоянной.
Вычислим ее. Кинетическая энергия определяется движением
шарика (пружина считается невесомой):
mv 2 m (dr / dt ) 2
Ek
.
2
2
33

34.

Потенциальная энергия системы «содержится» в пружине, ее
нетрудно найти, определив работу, необходимую для растяжения
(сжатия) пружины на величину r:
r
r
0
0
r2
Eп Fdr kr dr k .
2
Для неизменной со временем величины Е = Ек + Еп (интеграла
энергии) получаем
m (dr / dt ) 2 kr 2
E
.
2
2
34

35.

Так как dE/dt 0, то, продифференцировав интеграл энергии по
t, приходим к выражению
dr d 2 r
dr
dr d 2 r
m
k r
m
kr 0,
dt dt 2
dt
dt dt 2
т. e. к уравнению движения шарика (1), проверив тем самым
правильность его получения.
35

36.

1.2.
Радиоактивный распад (закон сохранения массы)
При радиоактивном распаде одно вещество с течением времени
превращается в другое вещество. Пусть масса радиоактивного
вещества равна М. Рассмотрим изменение массы вещества за
некоторое время t. Между моментами t и t + t всего распадается
M = M(t + t) M(t) вещества.
36

37.

От чего зависит это изменение? Логика подсказывает, что это
изменение зависит от массы вещества, времени, в течение
которого распадается вещество, и от природы самого вещества.
Эту зависимость мы можем записать следующим образом:
M = М t.
Здесь знак « » говорит об убывании радиоактивного вещества,
коэффициент,
зависящий
от
природы
вещества
и
37
называемый постоянной радиоактивного распада.

38.

Это выражение можно переписать в виде
M
M ;
t
M t 0 M 0 .
38

39.

Переходя к пределу
M dM
,
dt
t t
lim
математическую
модель
распада
радиоактивного
вещества
запишем в виде
dM
M ,
dt
M t 0 M 0 .
39

40.

Решение этого уравнения имеет вид
М = M0e t.
С учетом М = m0N, где т0 масса одного атома, N
число
атомов в массе М, получаем закон радиоактивного распада
N = N0e t.
40

41.

1.3. Явление поглощения (закон сохранения энергии)
Для построения математической модели воспользуемся законами
сохранения числа фотонов и энергии. Рассмотрим явление
поглощения света в некоторой среде. Пусть на некоторую
поглощающую среду падает свет интенсивностью I (рис. 2).
x
I
I I
Рис. 2. Поглощение света в некоторой среде
41

42.

При прохождении через среду длиной х произойдет изменение
интенсивности
на
I= kI x,
где
k
коэффициент
пропорциональности, знак « » говорит об убыли интенсивности.
Переходя от приращений к дифференциалам, получаем
dI = kIdx.
42

43.

Представляя это уравнение в виде
dI
kI ,
dx
I x 0 I 0 .
получим математическую модель явления поглощения света.
Решение этого уравнения называют законом Бугера:
I = I0е kх.
43

44.

1.4. Спонтанное излучение (закон сохранения числа частиц)
Получим
математическую
модель
явления
спонтанного
излучения на основе сохранения числа частиц. Рассмотрим атом с
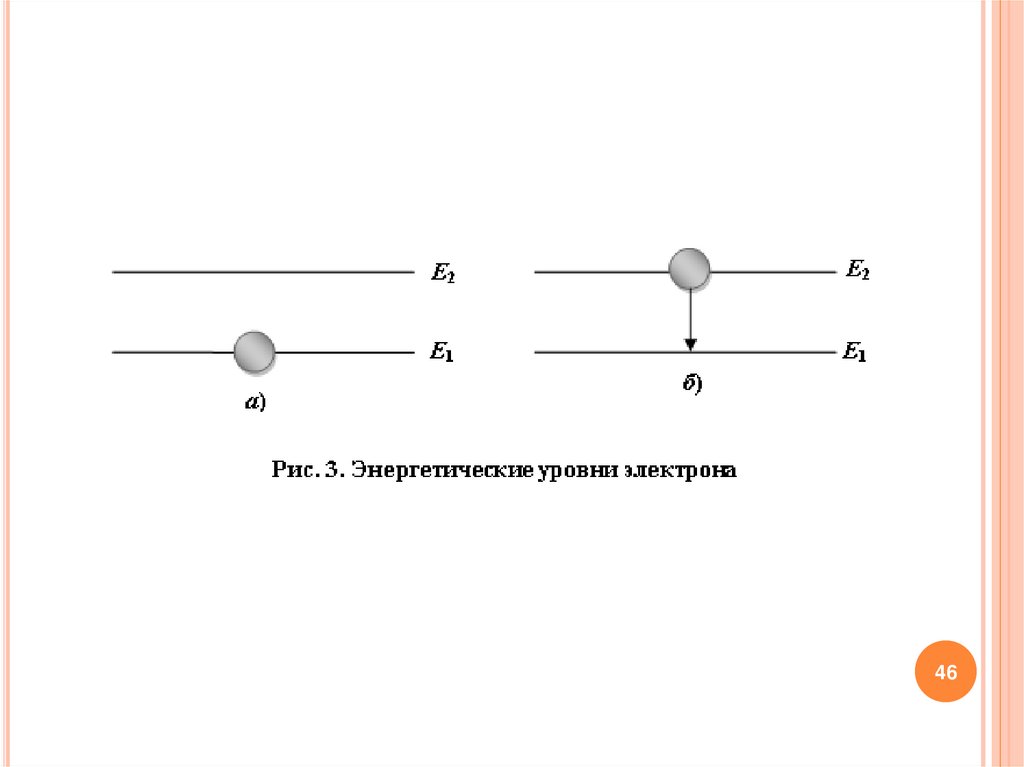
энергетической точки зрения. Если электрон находится на
основном энергетическом уровне E1, то говорят, что атом не
возбужден (рис. 3, а). Если электрон перевести на другой уровень
Е2, то атом переходит в возбужденное состояние.
44

45.

Любая система стремится к такому состоянию, в котором его
энергия минимальна, т.е. электрон через некоторое время
перейдет из возбужденного состояния Е2 в основное с наименьшей
энергией E1
кванта
(рис. 3, б). При этом он излучит свет с энергией
21 E2 E1 .
Явление излучения кванта энергии при
самопроизвольном переходе электрона в состояние с низкой
энергией называется спонтанным излучением.
45

46.

46

47.

Рассмотрим теперь N0 атомов, находящихся в возбужденном
состоянии в некотором объеме V с концентрацией атомов
п = N / V.
В результате переходов электронов с уровня Е2 на Е1 число
возбужденных
атомов
будет
уменьшаться.
Это
изменение
пропорционально числу атомов N, времени t и зависит от
свойств самого атома, т.е. от некоторого коэффициента :
N N t dN Ndt .
t 0
47

48.

Записывая это выражение в виде дифференциального уравнения
и учитывая начальные условия, получим
dN
N ,
dt
N t 0 N 0 .
Решение этого уравнения имеет вид
N N 0 e t ,
где = 1/ 0 называется постоянной спонтанного излучения. Здесь
0 имеет смысл среднего времени жизни электрона на верхнем
энергетическом уровне (в возбужденном состоянии).
48

49.

Таким образом, мы рассмотрели различные физические явления
и получили одну и ту же математическую модель в виде
y x ay ,
т.е. в виде обыкновенного дифференциального уравнения.
Примеров,
в
которых
описывает
различные
одно
по
дифференциальное
природе
реальные
уравнение
процессы,
существуют достаточно много. Из этого вытекает одно из свойств
дифференциальных уравнений универсальность уравнений.
49

50.

1.5. Реактивное движение
(закон сохранения импульса)
В основе реактивного движения лежит закон сохранения
импульса.
Основной
общеизвестен:
принцип
продукты
реактивного
сгорания
ракетного
движения
топлива,
расположенные в кормовой части, через выхлопные сопла с
большой скоростью выбрасываются назад, а сама ракета при
этом
отталкивается
вперед.
Непосредственное
применение
законов Ньютона в задаче о движении ракеты при определении ее
кинематических параметров приводит к неразрешимой проблеме
многих тел.
50

51.

При движении ракеты ее масса убывает, и ракету можно
рассматривать как материальную точку переменной массы, на
которую действует реактивная сила, являющаяся результатом
взаимодействия
ракеты
с
выбрасываемыми
газами.
За
промежуток времени dt между моментами времени t и t + dt часть
топлива выгорает, и масса ракеты уменьшается на dm.
Импульс ракеты до испускания равен
mv .
51

52.

После испускания импульс системы будет равным
dm u m ( t dt )v ( t dt ) dm u ( m dm )(v dv ).
где u скорость истечения газов.
Здесь использовано разложение
m ( t dt ) m
dm
dt O(dt 2 )
dt
v ( t dt ) v
dv
dt O(dt 2 ).
dt
52

53.

Приравнивая импульсы до и после испускания, по закону
сохранения импульса получаем
m ( t )v ( t ) ( m dm )(v dv ) udm .
Пренебрегая бесконечно малой величиной
(1)
dm dv , из уравнения
(1) переходим к равенству
md v dm ( u v ).
Разделив обе части на элемент времени, получаем
dv dm
m
( u v ).
dt
dt
(2)
53

54.

Сравнение этого уравнения с основным уравнением динамики
позволяет рассматривать правую часть его как выражение
реактивной силы, приложенной к точке с переменной массой.
Учитывая, что разность
(u v ) U
есть скорость истечения
газов относительно ракеты, запишем (2) в виде
dv
m
p,
dt
где p U (dm / dt ) реактивная сила.
54

55.

Отметим, что для современных топлив скорость истечения газов
относительно ракеты достаточно большая: U = 3.. 5 км/с. Если на
ракету действует еще внешняя сила, то получим уравнение
Мещерского
dv
m
p F.
dt
(3)
55

56.

Рассмотрим случай, когда ракета движется в безвоздушном
пространстве под влиянием только реактивной силы. Причем
относительная
скорость
истечения
частиц
постоянна
и
направлена противоположно скорости ракеты, тогда
dv
dm
m
U,
dt
dt
(4)
где dm / dt сила тяги ракетных двигателей.
56

57.

Уравнение (4) является математической моделью движения тела с
переменной массой. Найдем решение уравнения (4) и приведем к
виду
dv
d ln m
U.
dt
dt
Интегрируя, получим
v ( t ) v0 U ln
m0
,
m(t )
(5)
где v0, т0 скорость и масса в начальный момент.
57

58.

Если v0 = 0, при полном сгорании топлива получим формулу
Циолковского
m0
,
v ( t ) U ln
m p ms
(6)
где тр полезная масса (спутника), ms структурная масса (масса
конструкции ракеты, управления, топливных баков и т.д.).
58

59.

Обсуждение результатов
Формула (6) позволяет сделать фундаментальный вывод о
конструкции ракеты для космических полетов.
Введем величину = ms /(m0 mp) и рассмотрим предельный
случай. Чаще всего
m0 ≫ тр
и
тs ≫ mр,
тогда имеем
v = U ln(l / ). Для реальных значений = 0,1 и U = 3 км/с имеем
v = 7 км/с.
59

60.

Для вывода спутника на круговую орбиту необходима первая
космическая скорость v = 8 км/с.
Таким образом, даже в самой идеальной ситуации (полезная масса
равна
нулю,
отсутствие
сопротивления
воздуха
и
т.д.)
одноступенчатая ракета не способна достичь первой космической
скорости.
Вывод необходимо использовать многоступенчатые ракеты.
60

61.

Выводы
1. Даже в простейших ситуациях для построения модели может
потребоваться использование не одного, а нескольких
фундаментальных законов.
2. Прямое формальное применение фундаментальных законов к
объекту, рассматриваемому как целое, не всегда возможно. В
этих случаях требуется просуммировать элементарные акты
взаимодействия между его частями, принимая во внимание
свойства объекта (например, его геометрию).
61

62.

3. Одними и теми же моделями могут описываться совершенно
разные по своей природе объекты, подчиняющиеся разным
фундаментальным законам, и, наоборот, данному, закону
могут отвечать принципиально разные модели (например,
линейные и нелинейные).
4. Необходимо использовать все возможности для проверки
правильности построения модели (предельные переходы,
другие фундаментальные законы т. д.).
62

63.

2. Иерархический подход к построению моделей
(метод «от простого к сложному»)
Лишь в редких случаях бывает удобным и оправданным
построение математических моделей даже относительно простых
объектов сразу во всей полноте, с учетом всех факторов,
существенных для его поведения. Поэтому естественен подход,
реализующий принцип «от простого к сложному», когда
следующий шаг делается после достаточно подробного изучения
не очень сложной модели.
63

64.

При этом возникает цепочка (иерархия) все более полных
моделей, каждая из которых обобщает предыдущие, включая их
в качестве частного случая.
Построим такую иерархическую цепочку на примере модели
баллистического маятника.
64

65.

Задача. Баллистический маятник
Одним из примеров применения законов сохранения для решения
конкретных задач является так называемый баллистический маятник,
который часто используется для определения скорости пули.
65

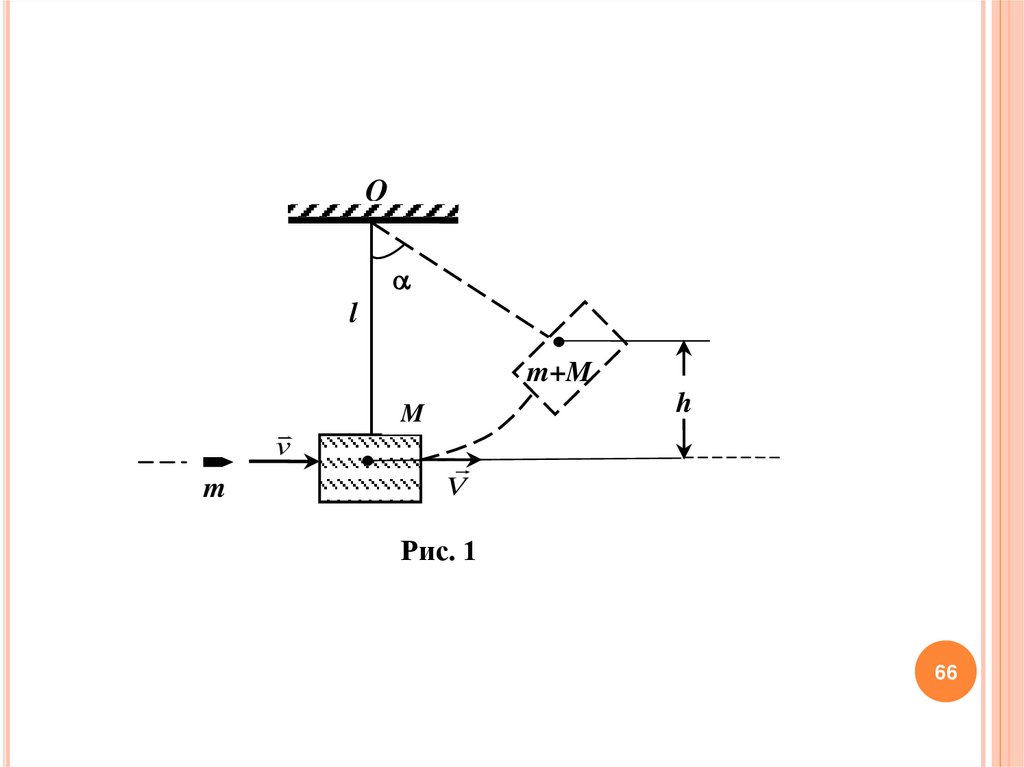
66.

O
l
m+M
v
m
h
M
V
Рис. 1
66

67.

Баллистический маятник – массивное тело, закрепленное в точке
подвеса
(например,
длинный
легкий
металлический
стержень,
подвешенный на гвозде). Трение в подвесе и массу стержня не
учитывать.
67

68.

Размеры и масса такого тела М таковы, что пуля массой m, летящая
горизонтально со скоростью v
и попадающая в массивное тело
маятника, застревает в нем, а сам маятник отклоняется от своего
положения равновесия. По отклонению маятника можно определить
скорость пули
v . Здесь l – длина стержня, l – расстояние от точки
подвеса до центра масс системы, угол наибольшего отклонения.
68

69.

1 способ
Пусть потенциальная энергия маятника в нижней точке равна нулю.
Пуля, застрявшая в грузе, сообщит системе «пуля – груз» свою
mv 2
кинетическую энергию
, которая в момент наибольшего
2
отклонения
стержня
от
вертикали
полностью
перейдет
в
потенциальную энергию системы.
69

70.

70

71.

Согласно закону сохранения механической энергии
mv 2
V2
( M m)
( M m ) gh.
2
2
Здесь V – скорость системы «пуля-груз» сразу после столкновения, g –
ускорение свободного падения, h – высота подъема центра масс
маятника.
71

72.

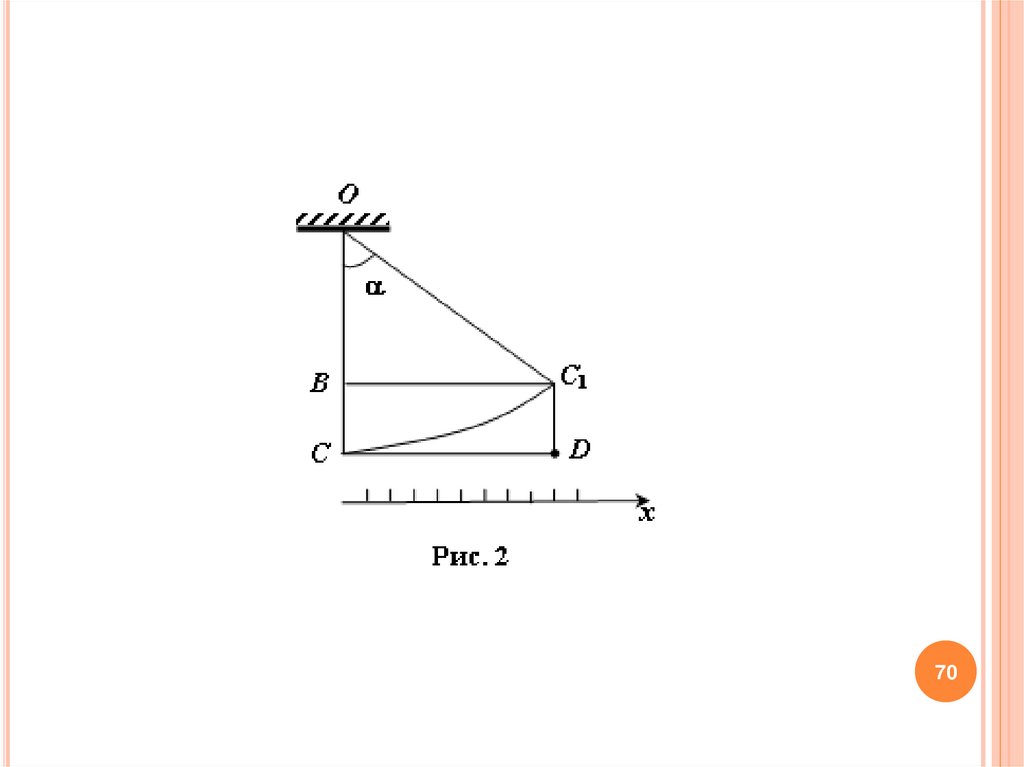
Определим h.
Длина стержня l = OC = OC1, поэтому из OBC1 катет ОВ = lcos . Высота
подъема груза равна
h = ВС = С1D = OC – OB = l – l cos = l (1 – cos ).
Таким образом,
mv 2
( M m ) gl (1 cos ).
2
72

73.

Искомая скорость определяется формулой
v
2( M m ) gl (1 cos )
.
m
Эта формула будет достаточно точной, если не учитываемые нами
потери энергии на разогрев пули и груза, на преодоление сопротивления
воздуха, разгон стержня и т. д. невелики.
73

74.

2 способ
Абсолютно неупругий удар – ударное взаимодействие, при котором тела
соединяются (слипаются) друг с другом и движутся дальше как одно
тело. При абсолютно неупругом ударе механическая энергия не
сохраняется: она частично или полностью переходит во внутреннюю
энергию тел (нагревание). Поэтому примененный в первом способе
закон
сохранения
механической
энергии
несправедлив
в
этой
ситуации: сохраняется полная, а не механическая энергия системы.
После неупругого столкновения маятник с застрявшей в нем пулей
будем рассматривать как материальную точку массы (M + m),
находящуюся в центре масс системы маятник-пуля.
74

75.

Скорость тел после неупругого удара можно определить из уравнения
закона сохранения импульсов, учитывая, что время соударения мало и
маятник за это время не успевает сместиться из положения равновесия.
Можно считать, что скорость центра масс маятника сразу после удара
направлена горизонтально, тогда проекция импульса системы на
горизонтальную ось сохраняется.
75

76.

До столкновения импульс системы p1 равен импульсу пули (маятник
покоится):
p1 m v
а импульс p2 системы сразу после неупругого столкновения равен:
p2 ( m M )V .
Так как при ударе импульс внешних сил равен нулю, то
mv = (m + M)V,
где V – скорость системы «пуля-груз» сразу после удара.
Кинетическая энергия системы сразу после столкновения
( m M )V 2
T
.
2
76

77.

В положении максимального отклонения маятника потенциальная
энергия U равна:
U = (m + M) gh
или
U = (m + M) gl(1 – cos ).
Пренебрегая потерями энергии на трение и сопротивление воздуха,
можно считать, что механическая энергия сохраняется:
U =T.
77

78.

Получили систему для определения скорости пули v:
mv ( m M )V
( m M )V 2
( m M ) gl (1 cos )
2
mv
V
(m M )
m M
v
2 gl (1 cos ) .
m
V 2 2 gl (1 cos )
78

79.

Начальная скорость пули
v
(m M )
2 gl (1 cos ) .
m
Полученная скорость пули в
m M
m
раз меньше, чем скорость пули
из способа №1.
79

80.

Замечание 1.
l (1 cos ) 2l sin
2
2
.
.
2 2
Угол мал, поэтому sin , sin
С учетом этого зависимость высоты от угла поворота стержня примет
вид:
l 2
h
2
(0)
80

81.

(0)
Из OBC1
BC1 x
sin
.
l
l
Подставляем
x
l
в (0) и получим выражение высоты подъема
через горизонтальное смещение х цилиндра:
x2
h
.
2l
Отсюда
v
m M
g
x .
m
l
81

82.

3 способ
Необходимо отметить, что систему «маятник-пуля» нельзя
считать замкнутой, так как на маятник во время удара действует
некомпенсированная
соответственно
сила
навстречу
реакции
пуле.
подвеса,
Однако
направленная
можно
считать
сохраняющейся проекцию момента импульса данной системы на
ось вращения в подвесе, так как проекция момента внешних сил
на эту ось равна нулю (пренебрегаем моментом сил трения,
действующим в подвесе).
82

83.

Найдем связь между начальной скоростью пули v и углом
отклонения маятника. Для этого используем два закона
сохранения.
83

84.

Рассмотрим систему «баллистический маятник-пуля».
На протяжении короткого времени интервала взаимодействия
пули и маятника момент импульса этой системы можно считать
постоянным, несмотря на действия силы тяжести.
импульса
пули
рассчитываем
как
момент
Момент
импульса
материальной точки относительно оси вращения: mvr, где
r – расстояние от точки подвеса до прямой, вдоль которой
движется пуля.
84

85.

Закон сохранения момента импульса в проекции на ось вращения
в нашем случае записывается
mvr = Iw + mVr,
(1)
где r = l – кратчайшее расстояние от точки подвеса маятника до
траектории движения центра масс (длина маятника), I – момент
инерции маятника относительно оси подвеса,
угловая скорость
w – начальная
маятника с пулей, V – скорость пули после
столкновения, которая, очевидно, связана с угловой скоростью
маятника
V = wr.
(2)
85

86.

При записи уравнения (1) пуля принимается за материальную
точку.
Угловая
скорость
маятника
выражается
через
начальную
скорость пули из (1) и (2)
w
mvr
I mr
2
(3)
86

87.

После
того
как
удар
закончился
действие
внутренних
диссипативных сил прекращается.
Поэтому после удара к процессам, происходящим с системой
«маятник-пуля» применим закон сохранения энергии.
87

88.

Кинетическая энергия системы после столкновения в нижней
точке
mV 2 Iw 2
T
.
2
2
(3)
Применим формулу (3) для угловой скорости w и исключая V,
получаем кинетическую энергию в виде:
T
m 2v 2 r 2
2
2( I mr )
.
(4)
88

89.

Потенциальная
энергия
системы
является
суммой
потенциальных энергий пули и маятника.
Положив потенциальную энергию системы в нижней точке
колебания равной нулю, для потенциальной энергии в высшей
точке имеем выражение:
U = mgh + Mghc,
где h и hc – высоты, на которые поднимаются центры тяжести
пули и маятника соответственно.
Считаем, что hc = h.
U = (m + M)gh.
89

90.

Окончательный вид потенциальной энергии в верхней точке:
U = (m + M)gl(1 – cos ).
(5)
Из условия сохранения механической энергии с учетом формул
(4), (5) находим выражение для начальной скорости пули v:
m 2v 2 r 2
2
2( I mr )
( m M ) gl (1 cos )
1
v
2( I mr 2 )( M m ) gl (1 cos )
mr
90

91.

Для упрощения расчетов будем считать маятник однородным
стержнем.
Тогда момент инерции маятника относительно оси
Mr 2
подвеса I
.
3
Получаем выражение для начальной скорости пули
1 2
v
( M 3m )( M m ) gl (1 cos ) .
m 3
91

92.

Замечание 2.
Центр масс (Ц-система). В любой системе частиц имеется одна
точка С, называемая центром масс, которая обладает рядом
интересных и важных свойств. Главным среди них является то,
что центр масс любой системы частиц движется так, как если
бы вся масса системы была сосредоточена в этой точке и к ней
были бы приложены внешние силы.
92

93.

Положение точки центра масс относительно начала координат
характеризуется радиусом-вектором
1
rC m i ri ,
m
(1)
где mi и ri масса и радиус-вектор i-й частицы; m масса всей
системы.
93

94.

Можно показать, что центр масс системы из двух частиц с массами т1 и m2 находится на прямой, их соединяющей, в точке С,
которая делит расстояние между этими частицами в отношении
l1 : l2 = т2 : m1. Продифференцировав (1) по времени, найдем
скорость VC
центра масс
1
VC m iVi
m
импульс же системы частиц равен
P m VC .
94

95.

Спасибо за внимание!
95