Математические модели и методы оптимизации процессов пространственного маневрирования морских подвижных объектов

1. Математические модели и методы оптимизации процессов пространственного маневрирования морских подвижных объектов при координированном

Математические модели и методы
оптимизации процессов пространственного
маневрирования морских подвижных
объектов при координированном воздействии
на рулевые устройства и силовую установку
Козлов Юрий Владимирович
Специальность 05.13.18 –
Математическое моделирование, численные методы и комплексы программ
Научный руководитель: к.т.н., с.н.с. каф. САиУ, ФТК
Симаков Игорь Павлович
1

2. Актуальность исследования

Проблема математического моделирования для автоматизации процессов
управления морскими подвижными объектами разрабатывается в течение
многих лет. В настоящий момент недостаточно исследован ряд
теоретических задач математического моделирования оптимального
управления процессами пространственного маневрирования ПА при
координированном воздействии на комплекс рулевых устройств (РУ) и
силовую установку (СУ). Потребность в решении таких задач возникает в
экстремальных ситуациях. Современные системы управления движением
(СУД) содержат автономно действующие функциональные подсистемы
управления и стабилизации отдельных координат объекта – курс, крен,
дифферент, глубина, скорость хода. Решение задач формирования
скоординированных управляющих воздействий на комплекс РУ и СУ
представляется проблемным.
Цель диссертационной работы
Разработка комплекса математических моделей для оптимизации и
повышения качества процессов маневрирования ПА по временным и
траекторным критериям за счет согласованного воздействия на рулевые
устройства и силовую установку.

3. Научные и практические задачи

Объект исследования
Математические модели подводного аппарата как наиболее сложного МПО.
Предмет исследования
Математические модели, численные методы и программное обеспечение
для оптимальной координации пространственного маневрирования ПА по
временным и траекторным критериям.
Научные и практические задачи
1.
2.
Разработка математических моделей объекта и моделей оптимальной
координации процессов пространственного маневрирования ПА на
основе НП с воздействиями на рулевую и силовую установки при
ограничениях на допустимые значения крена – потенциально-опасной
координаты.
Разработка обобщенных математических моделей нелинейных типовых
и функциональных элементов подсистем управления ПА, включающих
модели с непрерывными и разрывными характеристиками с
регуляризацией, создание методики оценки качества оптимальных
траекторий и параметров режимов движения МПО на длительных
временных участках маневрирования.

4.

3. Разработка комплекса численных методов НП для решения задач
координации с учетом невыпуклых функционалов и областей
допустимых решений, разработка структуры взаимодействия
координации и локальных подсистем, обоснование организации
координированного управления СУ и РУ (структуры КСУ).
4. Разработка программной реализации для вычислительных экспериментов
на основе общих математических моделей системы, включающих модели
пространственного движения ПА, разработка схемы координации
локальных подсистем управления с учетом нелинейных элементов.
Анализ предельных маневренных возможностей ПА и количественных
оценок результатов.
Методы исследования
Теория корабля, теория автоматического управления, теория оптимального
управления, теория конечномерной оптимизации, теория нелинейных
операторов для моделирования системы координации подсистем
управления.

5.

Научные положения, выносимые на защиту
1.
2.
3.
Математические модели ПА и методы оптимальной координации
подсистем управления – СУ и РУ на основе объединения методов
Лагранжа и дифференциального градиентного метода для процессов
пространственного маневрирования объекта.
Математические модели нелинейных элементов ПА с однозначными,
неоднозначными, непрерывными и разрывными характеристиками с
регуляризацией на основе алгебраических, дифференциальноалгебраических операторов.
Методы решения задач нелинейного программирования с выпуклыми и
невыпуклыми областями допустимых решений на основе сведения
системы необходимых условий к задачам Коши.

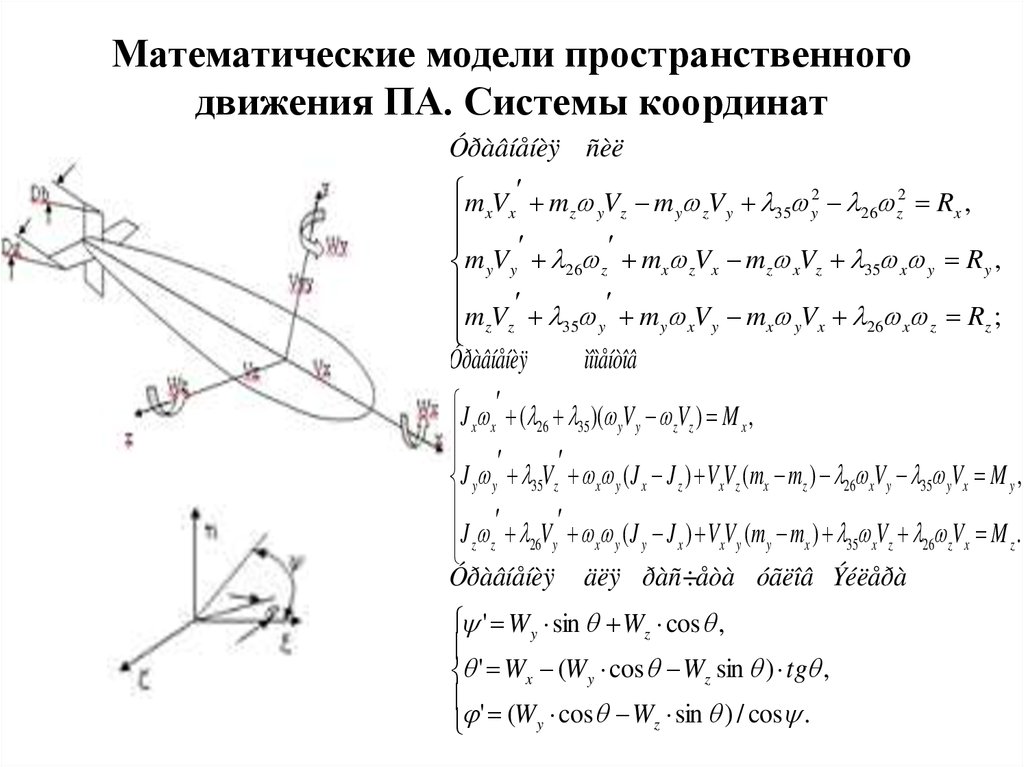
6. Математические модели пространственного движения ПА. Системы координат

Óðàâíåíèÿ ñèë
m V m V m V 2 2 R ,
z y z
y z y
35 y
26 z
x
x x
m
V
y y
26 z mx zVx mz xVz 35 x y R y ,
mzVz 35 y m y xVy mx yVx 26 x z Rz ;
Óðàâíåíèÿ
ìîìåíòîâ
J ( )( V V ) M ,
x
x x 26 35 y y z z
J y y 35Vz x y ( J x J z ) VxVz (mx mz ) 26 xVy 35 yVx M y ,
J z z 26Vy x y ( J y J x ) VxVy (my mx ) 35 xVz 26 zVx M z .
Óðàâíåíèÿ äëÿ ðàñ÷åòà óãëîâ Ýéëåðà
' Wy sin Wz cos ,
' Wx (Wy cos Wz sin ) tg ,
' (Wy cos Wz sin ) / cos .

7. Общие выражения для сил и моментов

Уравнения перемещения центра масс ПА в
земной системе координат
' Vx cos cos V y (sin sin cos cos sin )
Vz (cos sin sin sin cos ),
' Vx sin cos V y (cos sin sin sin cos )
Vz (cos cos sin sin sin ),
' Vx sin (V y cos Vz sin ) cos .
Общие выражения для сил и моментов
M x BV 2 (Cmx Cvmx ) D sin cos ;
M y BV 2 (Cmy Cvmy );
M z BV 2 (Cmz C mz ) D sin cos ,
Rx AV 2 (C x C x C xV ) Tx ;
Rz AV
2
(C z Cv );
Ry AV 2 (C y C y );

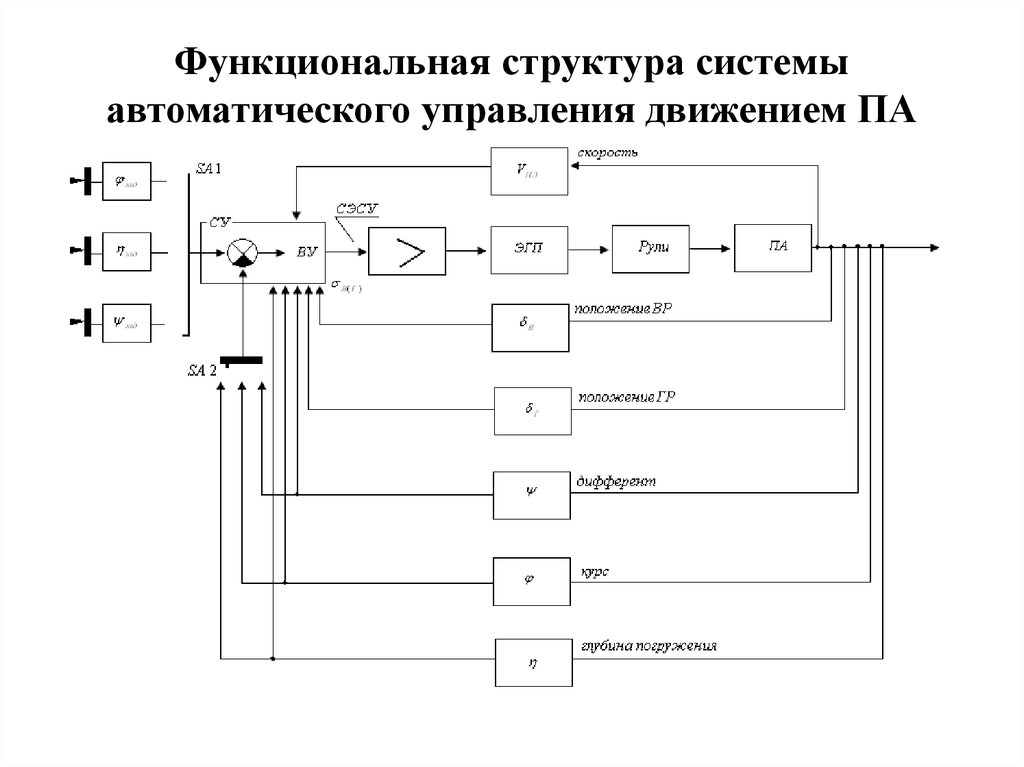
8. Функциональная структура системы автоматического управления движением ПА

9. Многоконтурная типовая структура системы управления глубиной ПА

10. Постановка задачи оптимизации управления ПА на циркуляции

Упрощенная модель движения
на установившейся циркуляции:
V cos( );
V sin( );
y ;
y aV ;
Система ограничений:
-ограничения по скорости хода
0 V V0 ,
-ограничения на угол перекладки
вертикального руля
0 0,
- ограничения на угол крена,
вытекающие из условия безопасности
bV 2 ;
c .
bV 2 0
Критерии оптимальности при экстренном маневре в горизонтальной плоскости:
- максимальная угловая скорость изменения курсового угла на установившейся
циркуляции, обеспечивающие минимальное время выхода на заданный курс и
минимальный радиус циркуляции
y aV max ïî V è ,
при выполнении ограничений на координаты.
R
V
1
min
y a

11.

12. Задача нелинейного программирования

f ( x) max ïðè îãðàíè÷åíè ÿõ g j ( x) 0, j 1,.., m, ãäå x x1 ,.., xN .
При этом относительно характера допустимой области решений, описываемой
системой неравенств, ничего не известно, кроме того, что она односвязная.
Относительно функции цели будем полагать, что она либо строго вогнута,
либо аффинна.
Рассмотрим два способа сведения системы неравенств, описывающих
допустимую область, к эквивалентному равенству.
I способ: Эквивалентное равенство, описывающее область допустимых
значений при задании ограничений в виде неравенств, имеет вид:
m
m
j 1
j 1
G( x) g j ( x) g j ( x) 0.
II способ сведения системы неравенств, описывающих допустимую
область, к эквивалентному равенству:
1) Система 2-х неравенств g1 ( x) 0 è g2 ( x) 0 равносильна уравнению
g1 ( x) g 2 ( x) g1 ( x) g 2 ( x) 0

13.

2) Система 3-х неравенств g1 ( x) 0, g 2 ( x) 0, g3 ( x) 0 равносильна уравнению
g1 g 2 g 3 g1 g 2 g1 g 2 g 3 g1 g 2 0
3) Система 4-х неравенств g1, 2,3, 4 ( x) 0 равносильна уравнению
g1 g 2 g 3 g 4 g1 g 2 g 3 g 4 g1 g 2 g 3 g 4 g1 g 2 g 3 g 4 0
Продолжая так далее, получим одно равносильное неравенство, задающее
допустимую область решений
,
Г ( x1 , x2 ,.., xi ,.., xN ) 0,
Эквивалентное равенство имеет вид
Г ( x1 , x 2 ,.., xi ,.., x N ) Г ( x1 , x 2 ,.., xi ,.., x N ) 0.
Приравнивая Ã ( x1 , x2 ,.., xi ,.., xN ) нулю, получаем уравнение границы
допустимой области решений (описание границы области одним уравнением).
Функция Лагранжа имеет вид:
L( x, ) f ( x) G ( x),
где 0 - множитель Лагранжа. И ограничения на область:
Г ( x1 , x 2 ,.., xi ,.., x N ) Г ( x1 , x 2 ,.., xi ,.., x N ) 0.

14. Решение задачи оптимизации параметров движения ПА на циркуляции

Модифицированная функция Лагранжа: L aV G (V , ) , где
и равносильное системе неравенств равенство имеет вид:
0
G (V , ) 0 V V0 V 0 bV 2 bV 2 0 V0 0 0.
Необходимые условия
экстремума имеют вид:
L
G
a
0
V
V
L
G
aV
0
L
G (V , ) 0
Градиентная система
дифференциальных уравнений:
G
dV
[
sign
(
a
)];
1
dt
V
G
d
2 [ sign( aV
)];
dt
d
dt 3[ sign(G (V , ))].
G
2bV [1 sign( 0 bV 2 )] sign(V ) sign(V0 V ),
V
G
bV 2 [1 sign( 0 bV 2 )] sign( ) sign( 0 ).

15.

Сходимость к решению из различных начальных условий

16. Отыскание оптимального решения на границе невыпуклой допустимой области («чистая» задача Лагранжа)

Исходные неравенства
1 0 0,
2 0 b V 2 0
равносильны одному неравенству
(V , ) 1 2 1 2 0
(V , ) ( 0 0 ) (1 b V 2 )
( 0 0 ) (1 b V 2 ) 0,
приравнивание которого нулю дает уравнение границы допустимой
области в неявном виде
Г (V , ) ( 0 0 ) (1 b V 2 )
( 0 0 ) (1 b V 2 ) 0.

17. Градиентная система уравнений отыскания оптимального решения на границе допустимой области

Функция Лагранжа
L(V , , ) a V Г (V , ) max,
Производная функции Лагранжа по времени
dL
Г dV
Г d
d
(a
)
(a V
)
Г
dt
V dt
dt
dt
Градиентная система
Г
dV
a
,
dt
V
d
Г
a
V
,
dt
d Г (V , )
dt
V (0) 0, (0) 0, (0) 0.

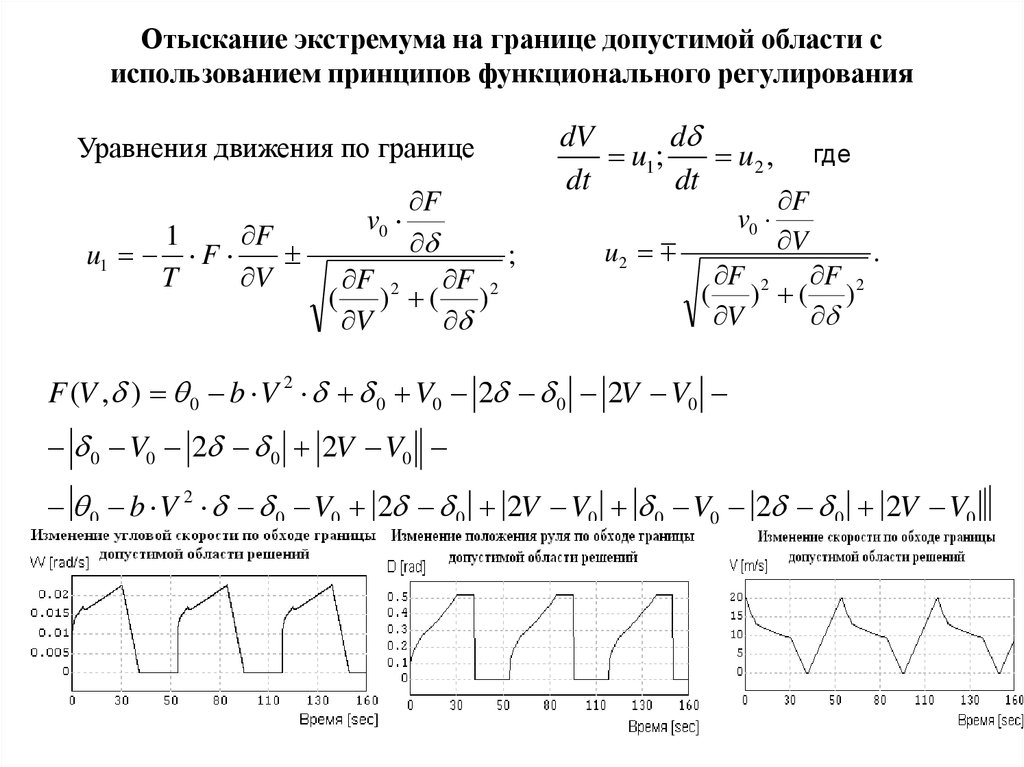
18. Отыскание экстремума на границе допустимой области с использованием принципов функционального регулирования

Уравнения движения по границе
u1
1
F
F
T
V
v0
F
F 2 F 2
( ) ( )
V
dV
d
u1 ;
u2 ,
dt
dt
;
v0
u2
(
где
F
V
F 2 F 2
) ( )
V
.
F (V , ) 0 b V 2 0 V0 2 0 2V V0
0 V0 2 0 2V V0
0 b V 2 0 V0 2 0 2V V0 0 V0 2 0 2V V0

19. Способы задания границы в явной форме (см. файл “delta_V.mrj”)

f (x)
Использование оператора выделения минимального сигнала
из двух
f 2 ( x)
входных
и f1 ( x)
1
1
f ( x) (1 sign ( f1 ( x) f 2 ( x))) f1 ( x) (1 sign ( f1 ( x) f 2 ( x))) f 2 ( x),
2
2
0
где f1 (V ) 0 и f 2 (V )
2
b V
1
0
1
0
0
0 (1 sign ( 0
)) (1 sign ( 0
))
2
2
2
2
b V
2
b
V
b
V
z
z
Применение оператора “сглаживания”
sign ( z )
z
z
,
1
0
z2
1
0
)
,
где
Уравнение границы ( 0
z
.
0
2
2
( z ) 2
b V 2
b V
“Сглаживая” и функцию
получаем еще
z
одно тождественное первому уравнение
границы
1
z2 1
(2 0 z )
.
2
z2 2
0
1
z2
1
( 0
)
.
2
2
b V
z2 2

20. Результаты «сглаживания» операторов

Значения
варьируем от 0,1 до 0,0001

21. Отыскание экстремума на границе допустимой области с использованием принципов функционального регулирования

dV
d
u1 ;
u2 ,
dt
dt
Уравнения движения по границе
u1
1
F
F
T
V
v0
F
F 2 F 2
( ) ( )
V
;
v0
u2
(
где
F
V
F 2 F 2
) ( )
V
.
F (V , ) 0 b V 2 0 V0 2 0 2V V0
0 V0 2 0 2V V0
0 b V 2 0 V0 2 0 2V V0 0 V0 2 0 2V V0

22. Основные характеристики оптимального маневра

Зависимости параметров движения от скорости хода

23. ОСНОВНОЙ РЕЗУЛЬТАТ выявлены оптимальные по критериям быстродействия и минимизации радиуса циркуляции значений перекладки вертикального

руля и скорости хода при осуществлении глубоких
маневров по курсу при различных ограничениях на допустимый угол крена
Полученное решение – скорость V*<Vном и δ=δо
ОБЕСПЕЧИВАЕТ ОДНОВРЕМЕННО
МИНИМАЛЬНОЕ ВРЕМЯ ВЫХОДА НА ЗАДАННЫЙ КУРС
И
МИНИМАЛЬНЫЙ РАДИУС ЦИРКУЛЯЦИИ

24. ПРИНЦИП КООРДИНИРОВАННОГО УПРАВЛЕНИЯ СУ И РУ

доп
ПРИНЦИП КООРДИНИРОВАННОГО УПРАВЛЕНИЯ
СУ И РУ
Принцип управления экстренным маневром корабля по курсу как
объектом с двумя управляющими воздействиями (на силовую
установку и на рулевое устройство) прост и его вербальная
формулировка такова.
При получении команды на маневр должны быть выполнены следующие
операции:
- управление силовой установкой должно обеспечить в экстренном
порядке переход от любой начальной на оптимальную скорость ;
*, должно переключаться с регулятора
- управление вертикальнымVрулем
стабилизации угла курса на регулятор угла крена с заданием ему
уставки
(“+” или “-” в зависимости от направления маневра);
доп
- при входе угла курса в зону
его стабилизации
все
переключения осуществляются в обратную сторону:
(t ); Зад (t )
- регулятор скорости хода - на заданную “рукояткой”
- рулевое устройство – на авторулевой.

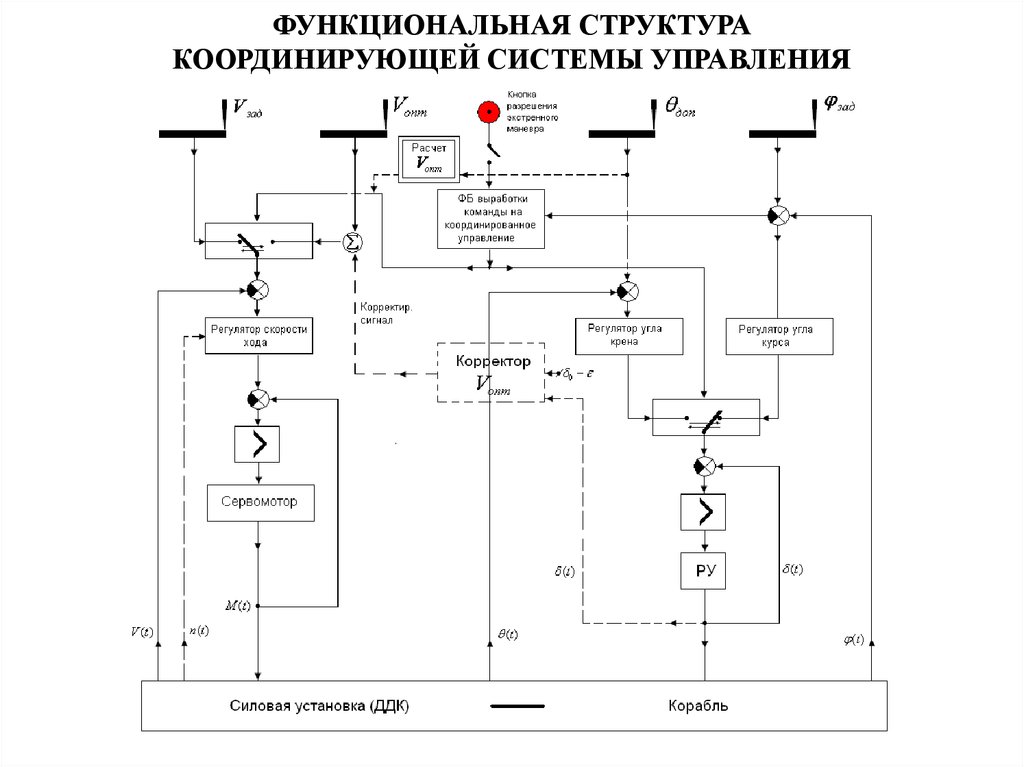
25. ФУНКЦИОНАЛЬНАЯ СТРУКТУРА КООРДИНИРУЮЩЕЙ СИСТЕМЫ УПРАВЛЕНИЯ

26. Алгоритмы координированного управления СУ и РУ

Модель регулятора скорости хода
1
M ( V V 1.1 1.1) , (0 M 1.1)
2
где V - вырабатываемый локальной системой регулирования скорости хода по ПИзакону
(1)
( 2)
V KV (Vпр V ) KV (Vпр V )dt.
Модель (алгоритм работы) регулятора курсового угла (авторулевого)
K [( зад ) (k1( ) k 2( ) V )
d
].
dt
Модель (алгоритм работы) регулятора крена, воздействующего на вертикальный руль
d
],
dt
где зад будет принимать значения доп или
от направления маневра
доп в зависимости
K [( зад ) k
корабля.
1
Признак «глубокого» маневра П М (1 sign ( S )) Признак
стабилизации
.
где
при , например,
(или2 5 град).
0.рулевым
1 рад
S ( (координированного
t ) зад ),
Алгоритмы
управления
устройством
Алгоритмы координированного управления силовой установкой
1
П С (1 sign ( S )) ,
2
П С П М
V пр П С V зад П М Vопт

27.

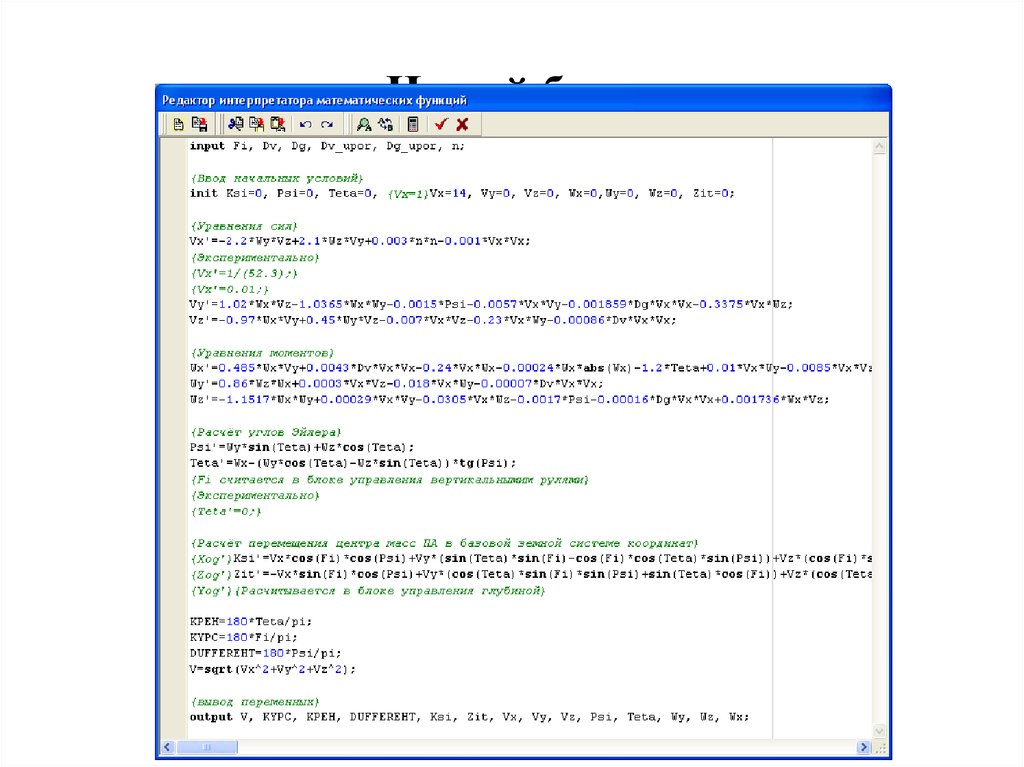
РАЗРАБОТКА В СРЕДЕ ПК «МВТУ»
моделирующего комплекса для подтверждения эффективности
предложенных принципов координированного управления
Задачи разработки:
-
-
-
-
Разработка полной компьютерной модели динамики
пространственного движения «гипотетического» ПА с моделями
локальных систем управления
Развитие методов моделирования существенно нелинейных звеньев
систем управления с динамическими кусочно-линейными и кусочноразрывными характеристиками (рулевых устройств с учетом
«упоров», «гистерезисных» законов управления, звеньев типа
«люфт», типа «медиана» и других)
Реализация эффективных способов отображения результатов
моделирования как в виде графиков изменения во времени
определяющих переменных (глубины, курса, скорости, крена,
дифферента, положения рулей, частоты вращения гребного винта),
так и в виде траекторий перемещения центра тяжести ПА в Земных
осях координат.
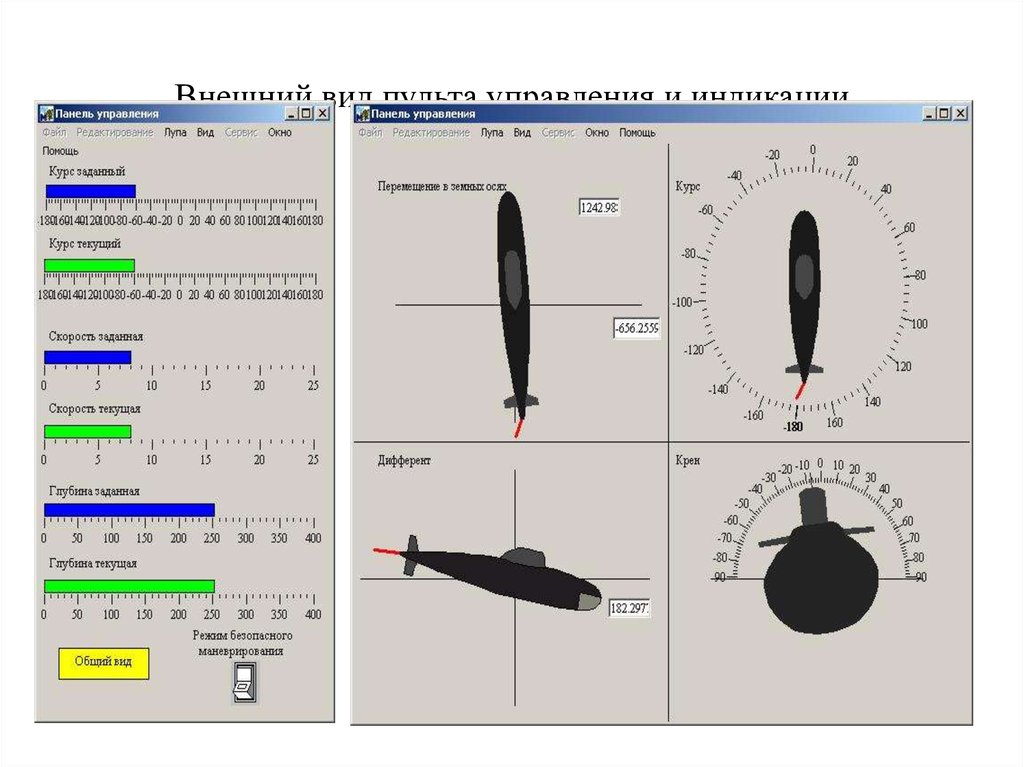
Реализация виртуальных панелей пультов управления с задатчиками
координат и режимов маневрирования, шкальных показывающих
приборов и информационных панелей для визуализации линейных и
угловых перемещений корпуса ПА с «анимационными эффектами».

28. Типовые нелинейные звенья САР с однозначной характеристикой

n
y K 0 K i ( x ai ( x ai ))
i 1
n
yi* ( x ai ) K 0 K i ( a j ai (a j ai )),
i 1
j 1,2,...n;

29. . Нелинейное звено типа «ограничение выходного сигнала с зоной нечувствительности»

B2
y ( x)
( x a1 x a2 a1 a2 )
2(a1 a2 )
B1
( x a3 x a4 a4 a3 ).
2( a4 a3 )

30. Двухполостной сервомотор с золотниковым усилителем

1
(1 sign ( y y ))
dy
2
f ( x)
dt
q 1 ( sign ( y y ) sign ( y y ))
2
1
q 1 sign ( f ) .
2

31.

Традиционное предикатное описание СМ
при
f ( x)
при
dy
при
dt
0
при
y y y и f ( x) 0
или
y y y и f ( x) 0
y y и f ( x) 0
или
y y и f ( x) 0,

32. Математическая модель гидравлического сервопривода регулирующего клапана турбины

D
M
Управление
M0
Управление
M
0
d
(1 í ) v ( í â ) f ( ) ,
dt
где н , в и v вычисляются по формулам:
1
í ( ) (1 Sign )
;
2
1
â ( ) (1 Sign ( 0 ) ;
2
1
v( ) (1 Sign ) .
2

33. Модель рулевой машины - нелинейное динамическое звено типа «упор»

Уравнения
dD
dt [(1 н ) ( н в )] F ( ), где
( D ) (1 sign( D )) 1 ,
н
2
( D ) (1 sign( D D )) 1 ,
в
0
2
1
( ) (1 sign( ))
2

34. Уточненные математические модели нелинейного звена типа «люфт»

e(t ) x(t ) y (t )
y (t ) u ( sign (e b) sign (e b)) 1
2

35. Моделирование звена «люфт»

Переходные процессы
Фазовая плоскость

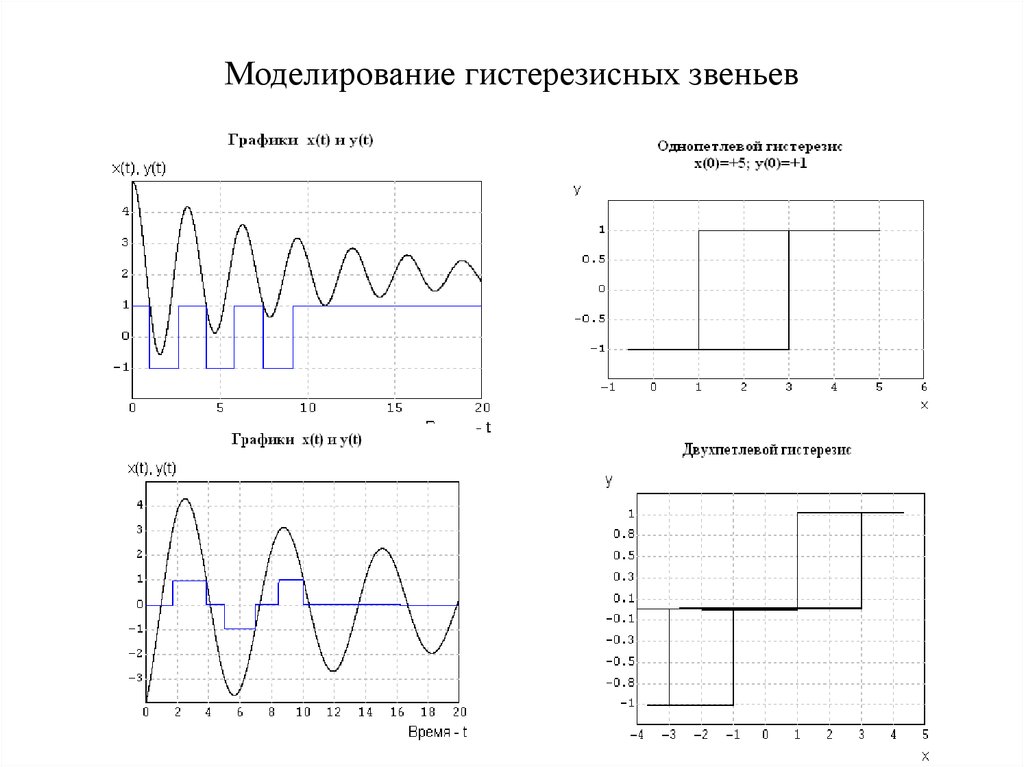
36. Гистерезисные звенья

Однопетлевой
Двухпетлевой
y ' v;
1
1
v ( x b2 ) u (1 sign (u )) (1 sign ( y y )) ( x b1 ) u
2
2
1
1
(1 sign (u )) (1 sign ( y y ))
2
2
y v,
1
1
1
1
v ( x b2 ) u (1 sign (u )) (1 sign ( y y 0 )) ( x b4 ) u (1 sign (u )) (1 sign ( y y 2))
2
2
2
2
1
1
1
1
( x b3 ) u (1 sign (u )) (1 sign ( y y 0 )) ( x b1 ) u (1 sign (u )) (1 sign ( y y ))
2
2
2
2

37. Моделирование гистерезисных звеньев

38. «Новый блок»

39.

40. ВАРИАНТ ВИРТУАЛЬНОГО ПУЛЬТА УПРАВЛЕНИЯ

41. Внешний вид пульта управления и индикации

42. Внешний вид дополнительных панелей анимации

43. Внешний вид дополнительных панелей анимации

44. Результаты вычислительных экспериментов на полной математической модели ПА

Эксперимент 1

45. Результаты вычислительных экспериментов на полной математической модели ПА

Эксперимент 2

46. Сравнение результатов 1 и 2 экспериментов

Траектории движения центра масс
R цирк.= 500 м
R цирк.>1000 м
Время перехода на заданный курс 180 град.
Время 180 сек
Время 320 сек

47. Результаты вычислительных экспериментов на полной математической модели ПА

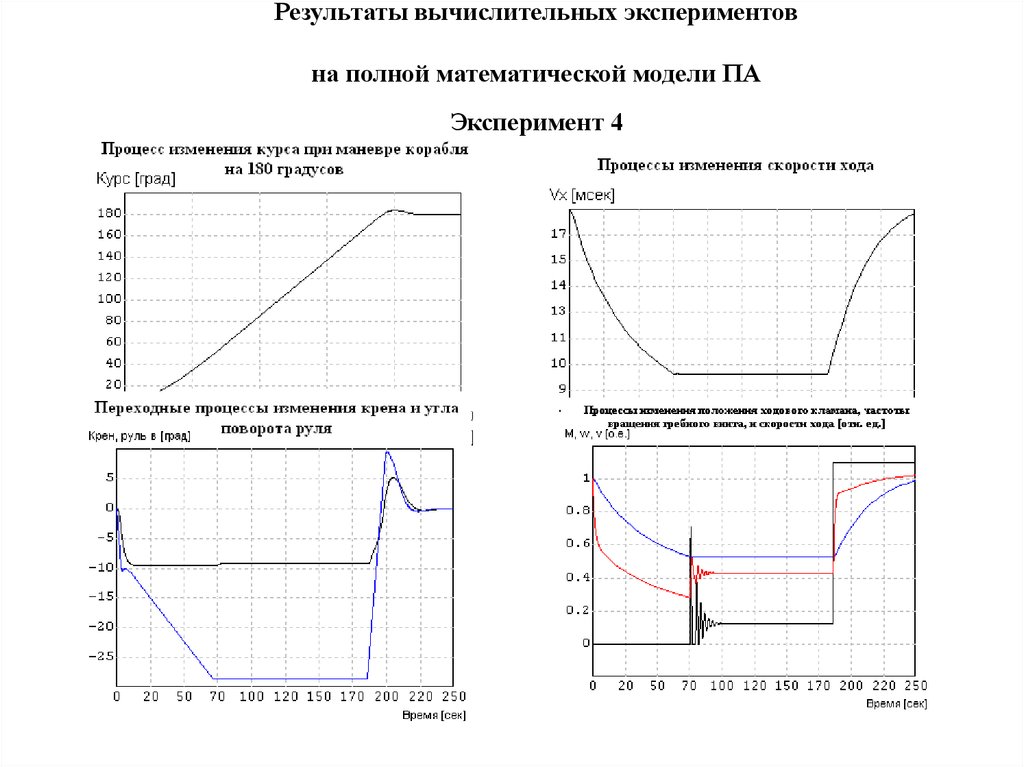
Эксперимент 3

48. Результаты вычислительных экспериментов на полной математической модели ПА

Эксперимент 4

49. Сравнение результатов 3 и 4 экспериментов

Траектории движения центра масс
R цирк.= 1700 м
R цирк.= 500 м
Время перехода на заданный курс 180 град.
Время 320 сек
Время 180 сек

50.

При выполнении вычислительных экспериментов решены следующие задачи:
1. Систематизированы основные положения математического моделирования динамики комплекса
«Подводный аппарат – рулевые устройства – двигательно-движительный комплекс»
2. Разработаны оригинальные математические модели существенно нелинейных динамических
элементов, в частности, сервоприводов с ограничениями их скоростных характеристик и
нелинейностями типа «упор», гистерезисных элементов, аналоговых мажоритарных элементов.
Предложенные модели отмеченных и других типовых нелинейных звеньев исключают
необходимость в использовании сложных предикатных описаний условий их функционирования.
3. Разработана и программно реализована в среде отечественного Программного Комплекса
«Моделирование в технических устройствах» полная математическая модель пространственного
движения «гипотетического» подводного аппарата (ПА) для целей исследования новых принципов
управления и проектирования функциональных и алгоритмических структур систем управления
рулевыми устройствами и двигательно-движительным комплексом с отображением результатов
моделирования в виде графиков изменения во времени определяющих переменных (глубины, курса,
скорости, крена, дифферента, положения рулей, частоты вращения гребного винта) и в виде
траекторий перемещения центра тяжести ПА в Земных осях координат.
4. Отработана технология создания в среде «МВТУ» виртуальных панелей пультов управления.
Продемонстрирована возможность обеспечения на виртуальных панелях пультов визуализации
фактических угловых перемещений корпуса ПА (крена, дифферента и других параметров), то есть
реализации «анимационных эффектов».
5. Проведена серия вычислительных экспериментов по исследованию принципов и алгоритмов
координированного управления рулевыми устройствами кормовых горизонтальных и вертикальных
рулей и двигательно-движительным комплексом при оптимизации процессов пространственного
маневрирования ПА по временным и траекторным критериям в экстремальных режимах при
ограничениях на потенциально опасные координаты крен, дифферент), накладываемых условиями
безопасности плавания.

51. Основными научными результатами, полученными в диссертации, являются:

1. Сформулирована и исследована задача комплексного управления процессами
пространственного маневрирования ПА как многомерного объекта с несколькими
управляющими органами различной физической природы – гидродинамическими рулями
(КГР, ВР) и силовой энергоустановкой с движителями при учёте реальных ограничений и
динамических характеристик средств (объектов) и ограничений на координаты движения
корабля.
2. Выявлен ряд новых ранее неизвестных свойств ПА как многомерного объекта
оптимального управления, определены структуры оптимальных траекторий, роль и
взаимодействие рассматриваемой совокупности управляющих органов при оптимизации
различных режимов пространственного движения объекта, а также его экстремальные
(предельные) маневренные свойства (характеристики).
3. Предложены новые способы и разработаны оригинальные алгоритмы координированного
управления автоматизированными рулевыми машинами и силовой установкой (ДДК),
обеспечивающие близкие к оптимальным по быстродействию:
- маневры ПА по курсу с одновременной минимизацией радиуса циркуляции;
- пространственные маневры корабля по курсу и глубине с одновременным изменением курса и глубины.
4. Разработаны новые эффективные способы и алгоритмы управления координатами
объекта с помощью комплекса рулевых органов, основанные на учёте естественно
возникающих при циркуляции сил и моментов на корпус, а также сил от изменения угла
крена в процессе осуществления маневров.
5. Разработаны имитационные модели динамики комплекса «ПА – ДДК – рули»,
обеспечившие возможность формулировки общих выводов о принципах организации
систем управления процессами пространственного маневрирования подводными
аппаратами.

52. Практическое значение работы состоит в следующем:

1. В среде отечественного ПК «МВТУ» разработана имитационная
математическая модель (ИММ) автоматизированного ПА с элементами анимации
и виртуальным пультом управления, обеспечившая возможность выявления
специфических свойств ПА как объекта оптимального управления путем
проведения целенаправленных вычислительных экспериментов.
2. Отработана технология создания ИММ не только для целей исследования
процессов управления, но и для создания компьютерных тренажеров, а также
имитаторов для проведения функциональных испытаний реальной аппаратуры
систем управления.
3. Разработана инженерная методика синтеза алгоритмов координированного
управления в многоуровневой системе управления ДДК и рулями, основанная на
рациональном использовании возможностей аналитических методов и
компьютерного моделирования.
4. Разработаны принципиальные способы управления и функциональноалгоритмические структуры систем управления функциональным комплексом
средств движения и маневрирования ПА, обеспечивающие, на наш взгляд,
кардинальное повышение качества процессов управления не за счёт усложнения
подсистем управления отдельными видами ТС, а за счёт целесообразной
координации их взаимодействия в различных режимах использования.