Похожие презентации:
Сложение перпендикулярных колебаний
1. Сложение перпендикулярных колебаний
2.
x A cos 0t+
y B cos( 0t 0 )
x
cos 0t
A
3.
ycos( 0t 0 )
B
cos 0t cos 0 sin 0t sin 0
2
x
x
cos 0 1 2 sin 0
A
A
2
x
y
x
cos 0
1
sin
0
2
A
B
A
4.
2x
y
x
y
2
2
cos
cos
0
0
2
2
A
B
A
B
2
2
x
2
(1 2 ) sin 0
A
2
2
x
x y
2
y
sin
2
cos
0
0
2
2
A
AB
B
Уравнение эллипса
5.
0 mcos 0 1
sin 0 0
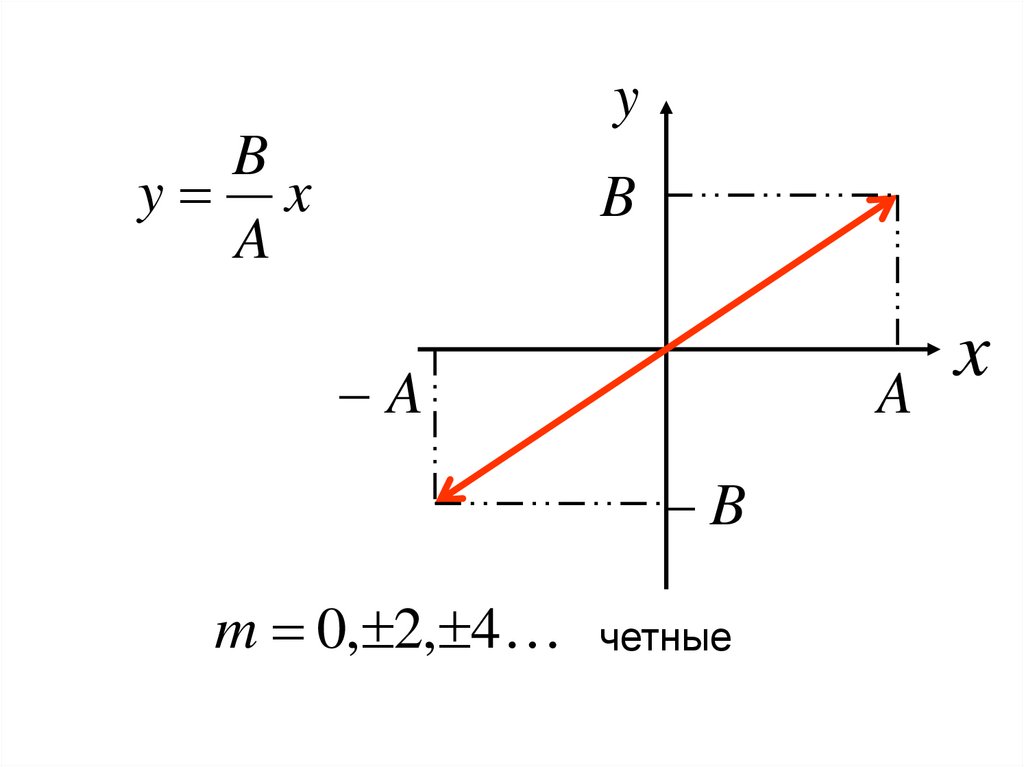
B
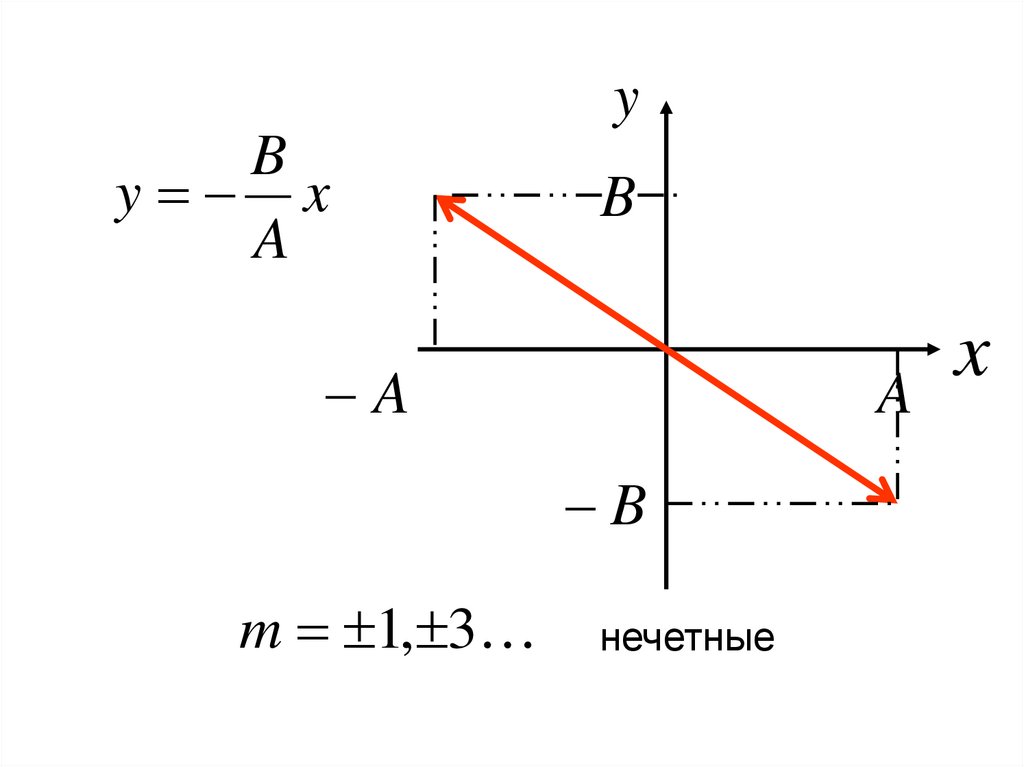
y x
A
-уравнение прямой
Линейно поляризованные колебания
6.
yB
y x
A
B
x
A
A
B
m 0, 2, 4 четные
7.
yB
y x
A
B
x
A
A
B
m 1, 3
нечетные
8.
0 (2m 1)2
2
sin 0 1
cos 0 0
2
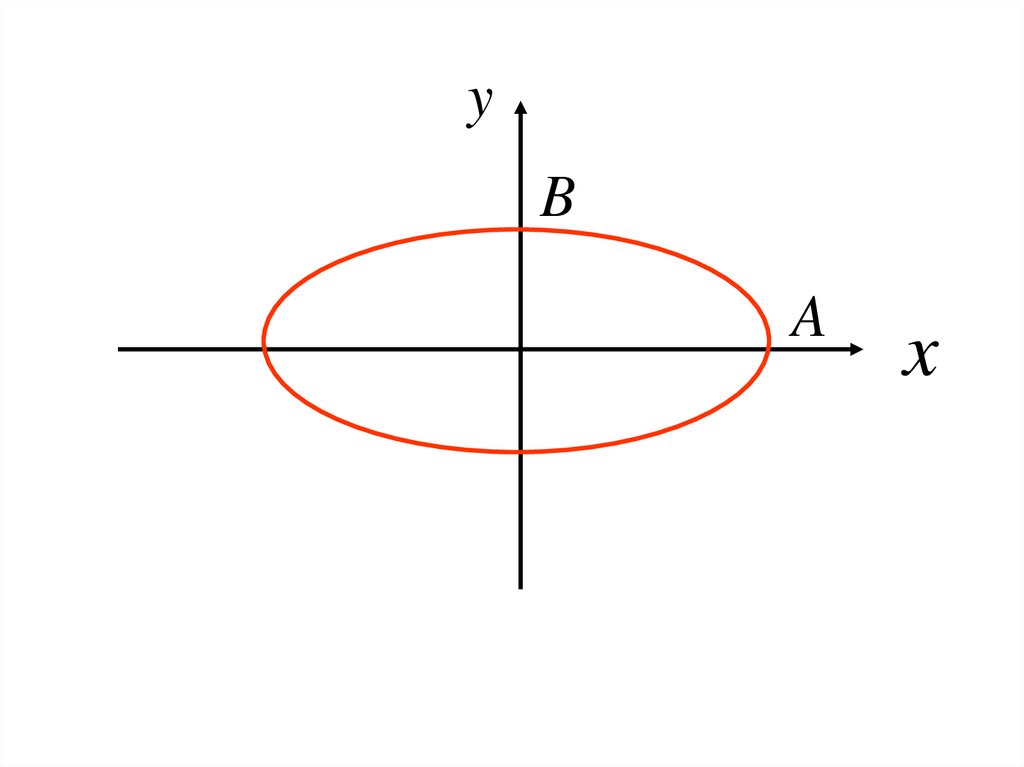
x
y
1
2
2
A B
-уравнение эллипса
эллиптически поляризованные
колебания
9.
yB
A
x
10.
• Если частоты складываемых колебанийразличны, то получаются сложные
траектории, называемые фигурами
Лиссажу
11. Затухающие колебания
• Затухающие колебания –амплитудакоторых с течением времени
уменьшается
12.
2d s
ds
2
2
s
0
0
2
dt
dt
s 2 s 0 s 0
2
s A0 e
t
cos( t )
Решение дифференциального уравнения
13.
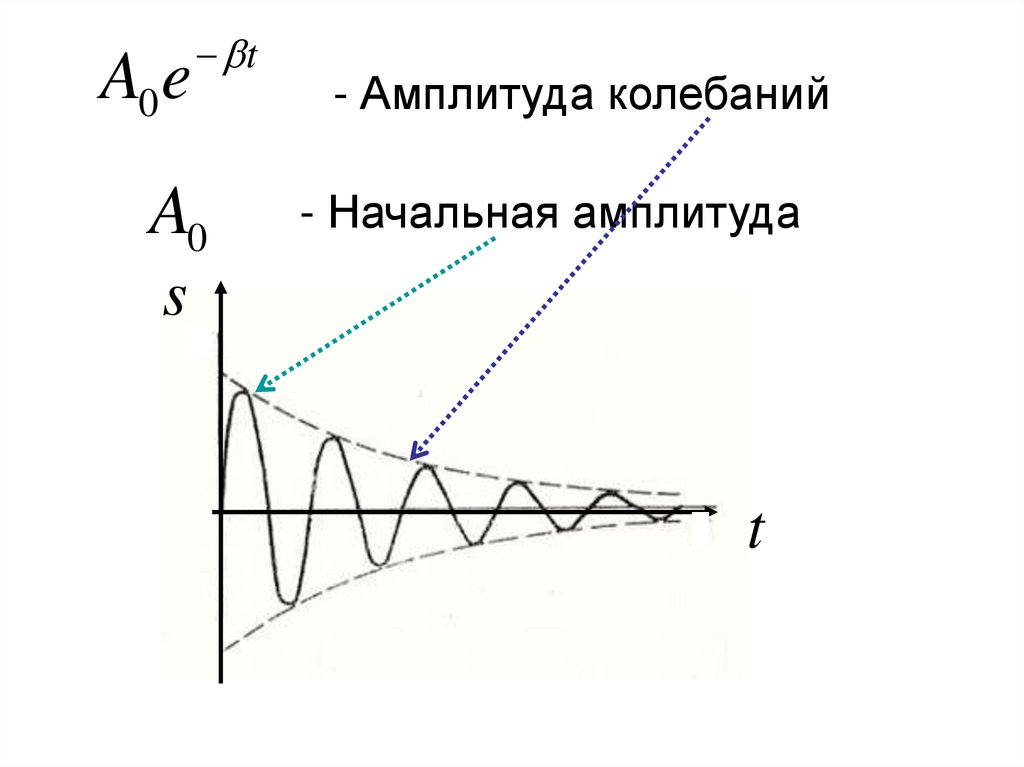
A0 et
A0
- Амплитуда колебаний
- Начальная амплитуда
s
t
14.
коэффициент затухания0 собственная частота
2
0
T
2
2
2
0
2
частота затухающих
колебаний
период затухающих
колебаний
15.
1- время релаксации
t
A(t )
A0 e
( t T )
A(t T ) A0 e
- декремент затухания
t
A0 e
A(t )
T
ln
ln
( t T )
A0 e
A(t T )
-логарифмический декремент
-затухания
- добротность
16.
При малом затухании0
2
2
2
T T0
0
0
2
17. Затухающие колебания пружинного маятника
F kxFТР rV
X- смещение маятника от положения
равновесия
Сила трения пропорциональна скорости,
r- коэффициент сопротивления
Знак «-» указывает, что сила трения и
скорость противоположно направлены
18.
ma m x F FТрm x rx kx 0
r
k
x x x 0
m
m
x 2 x 0 x 0
2
19.
k0
m
r
2m
2
2
0
x A0 e
t
2
k r
m 2m
cos( t )
2
20. Затухающие колебания в колебательном контуре
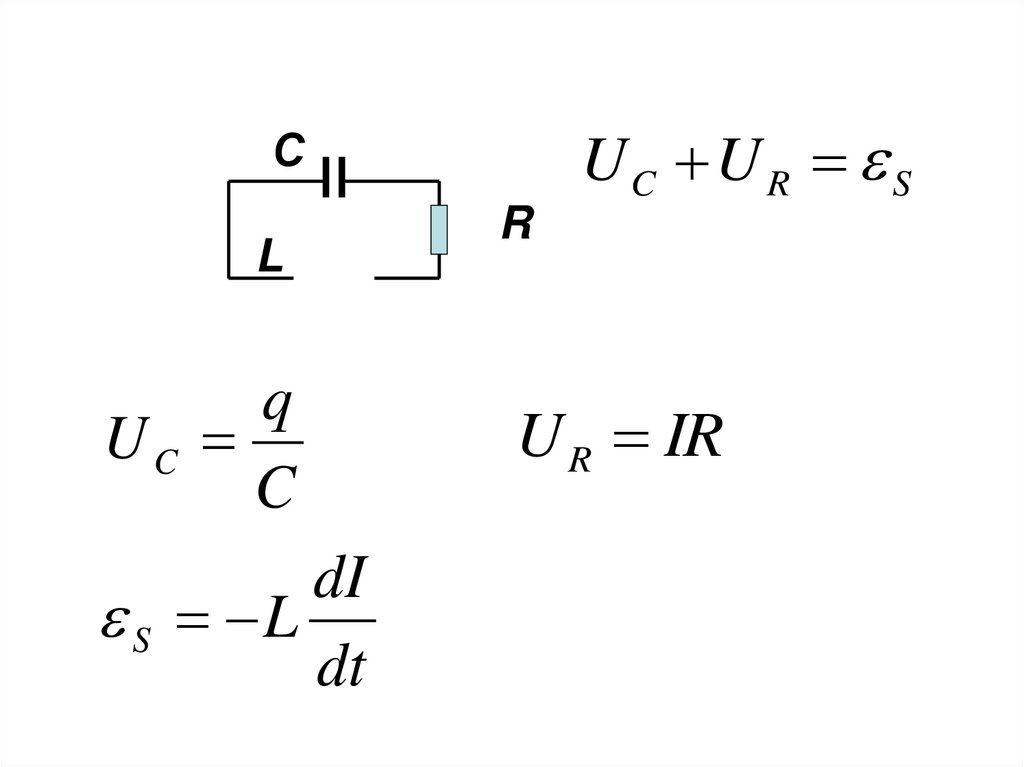
21.
UC U R SС
L
q
UC
C
dI
S L
dt
R
U R IR
22.
qdI
IR L
C
dt
dq
I
dt
2
dq
q
d q
R L 2
dt
C
dt
23.
dq qd q
0
L 2 R
dt C
dt
2
d q R dq 1 q 0
2
L dt LC
dt
2
2
q 2 q 0 q 0
24.
10
LC
R
2L
2
q q0 e
t
cos( t )
2
0
2
0
R 0
0
2
1
R
2
LC 4 L
25.
T0
2
1 L
R C
1
1
LC 2 R
2L
26.
20
2
0
2
1
R
2
LC 4 L
L
RКР 2
C
Критическое сопротивление,
при котором прекращаются
колебания

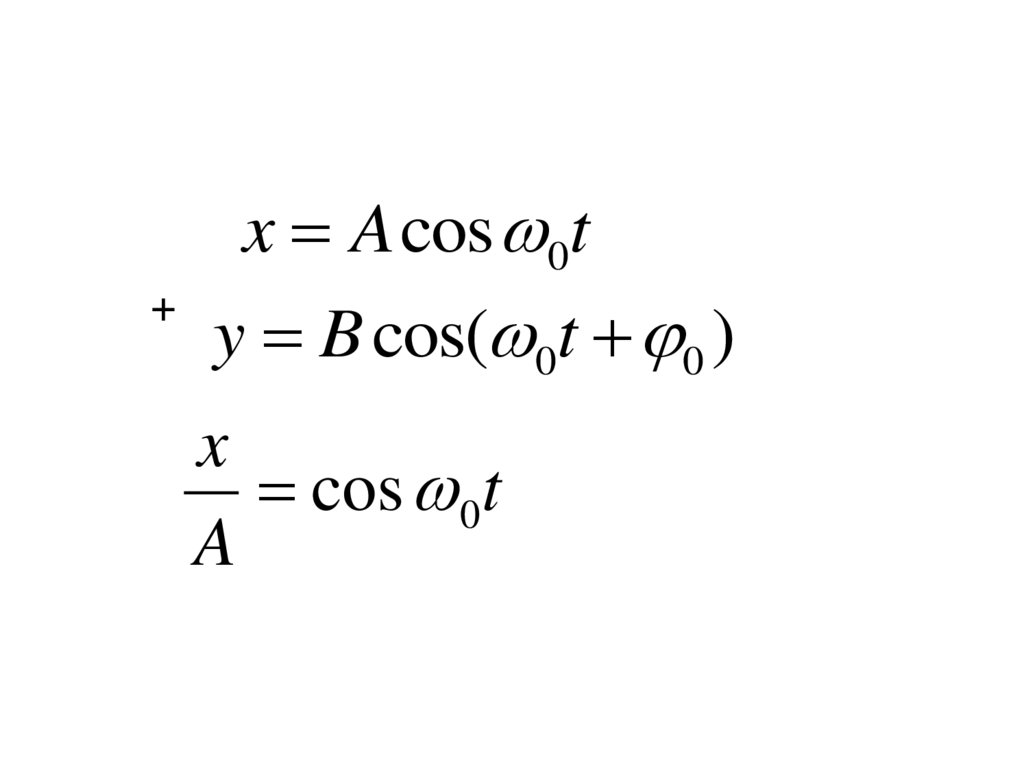
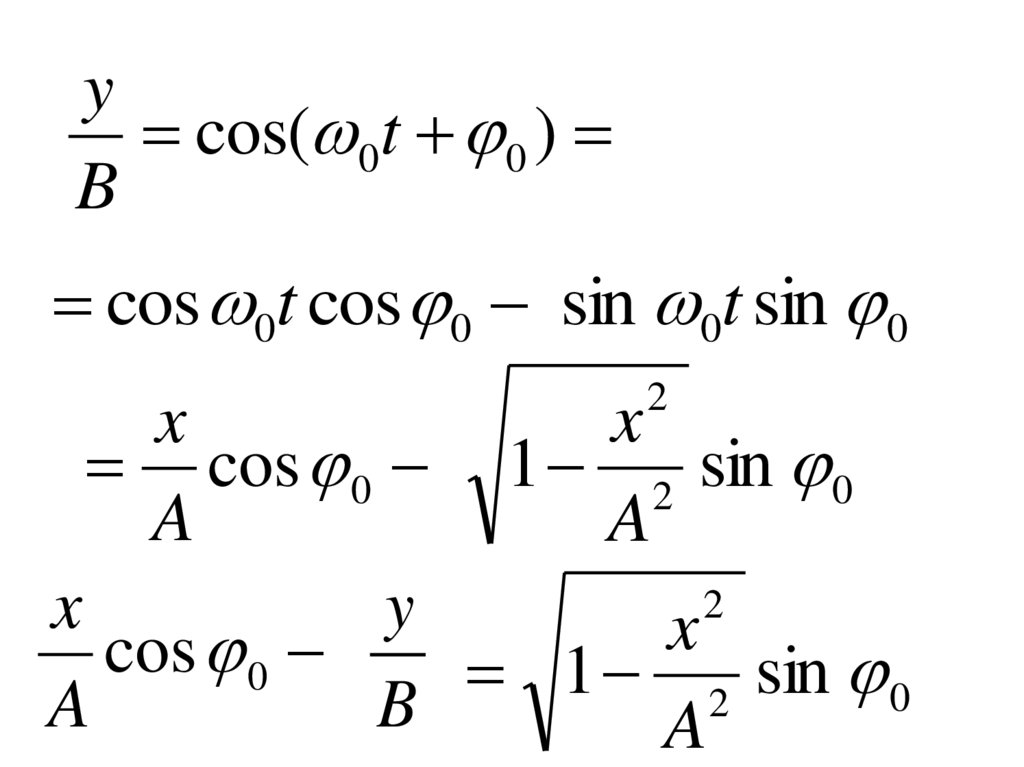
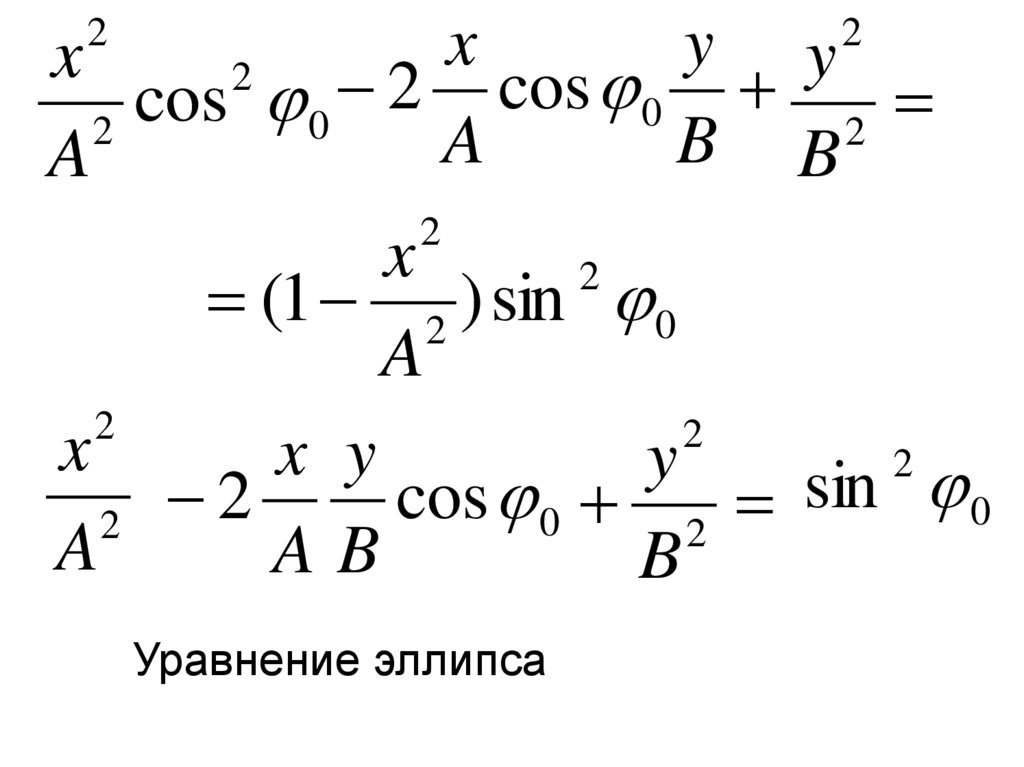









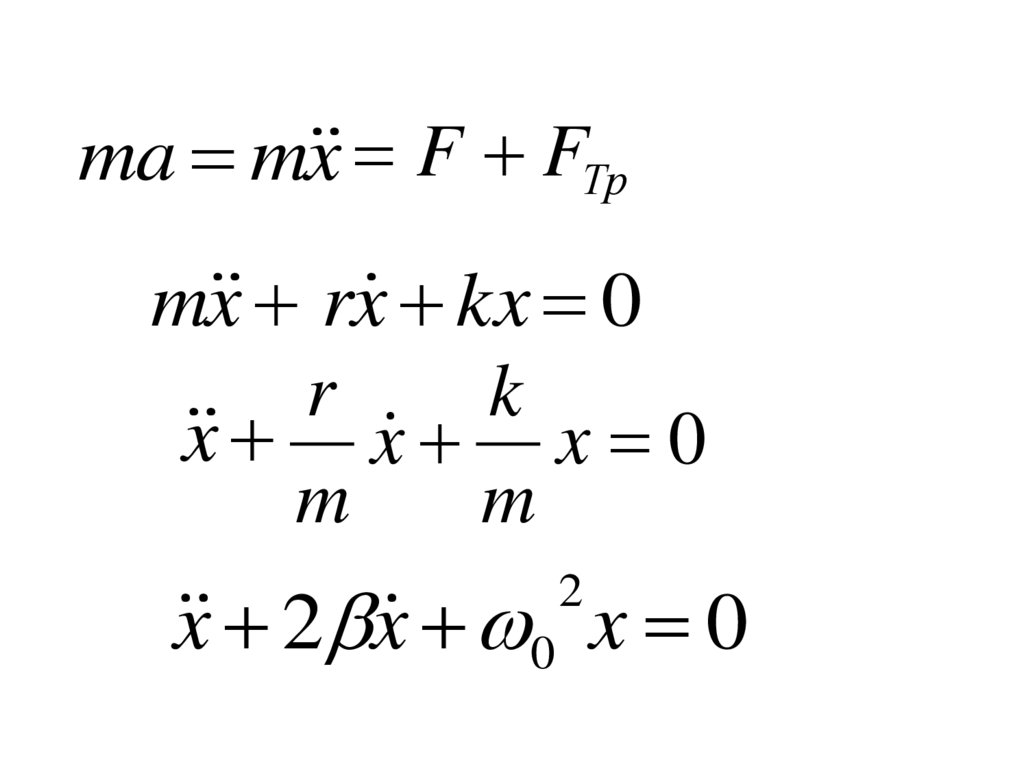
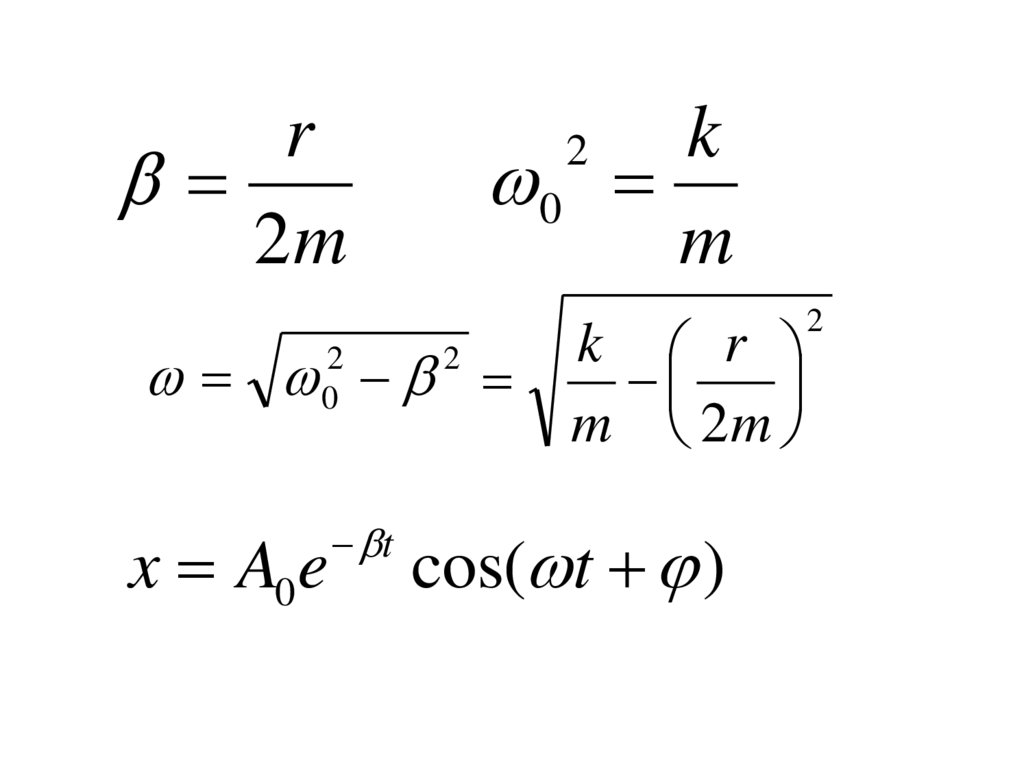

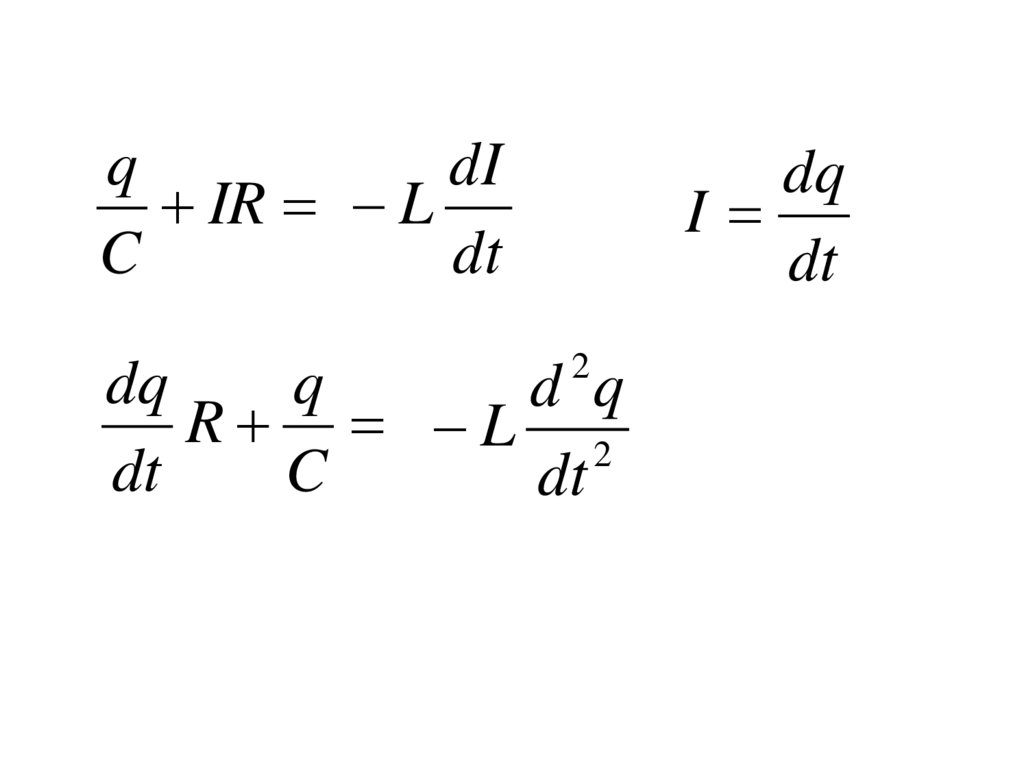
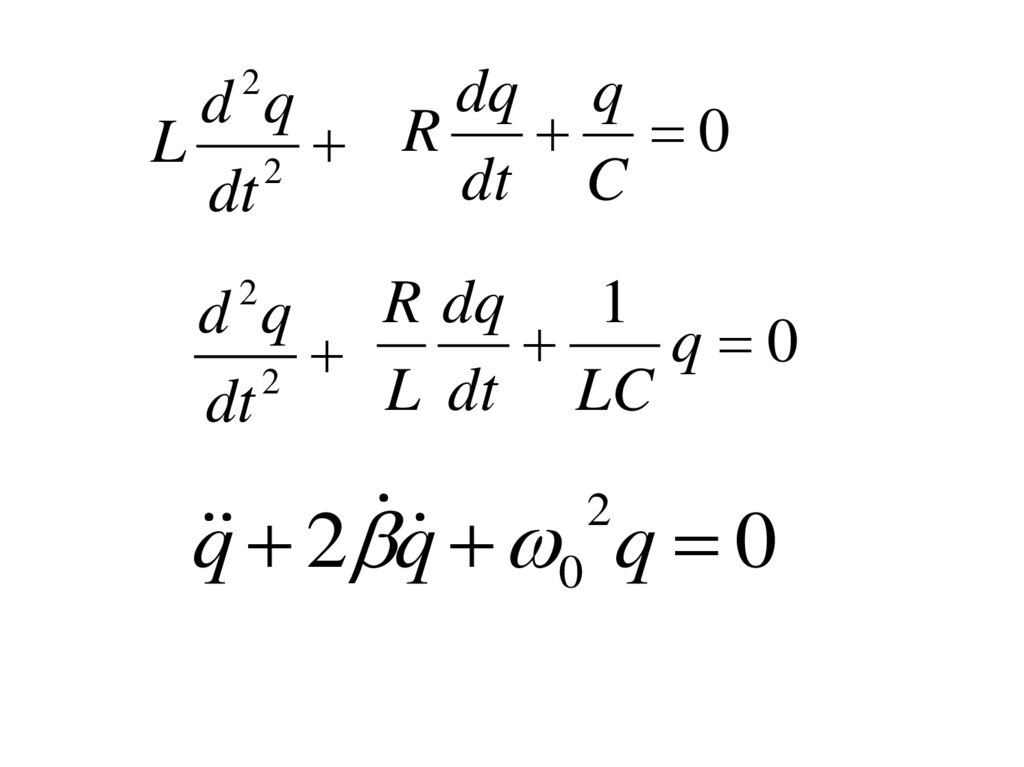

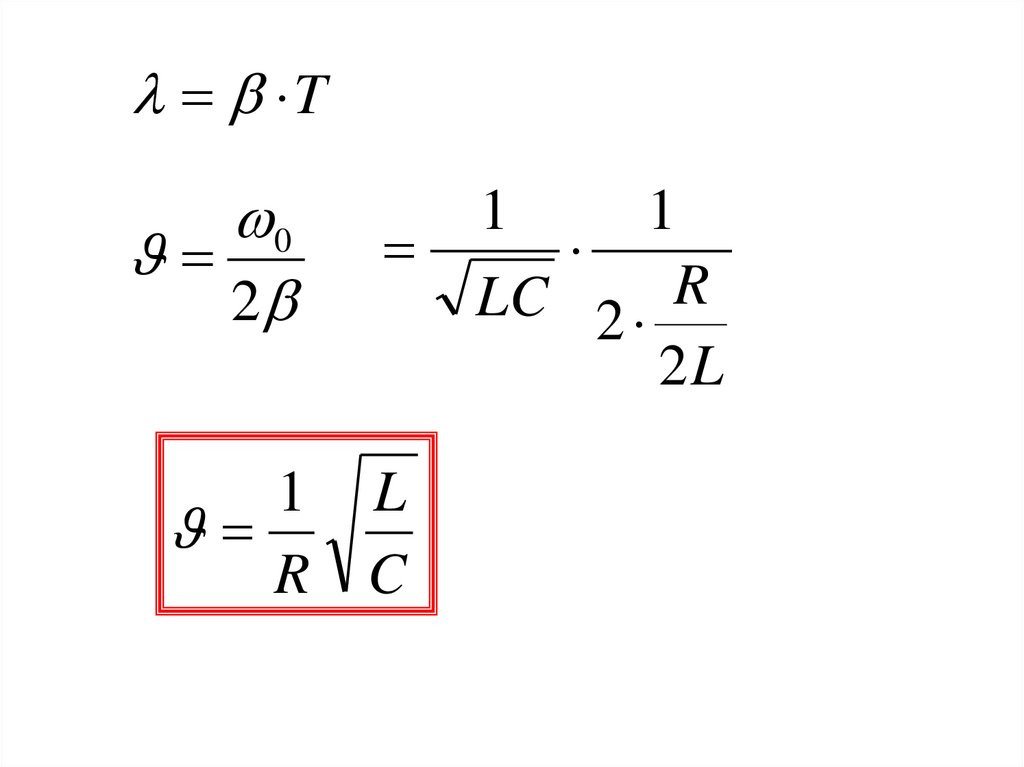

 Физика
Физика








