Похожие презентации:
Производная функции. Определение
1. Производная функции
ПРОИЗВОДНАЯФУНКЦИИ
2.
Определение:Предел отношения приращения функции к
приращению аргумента при ∆х → 0
называется производной функции f(x) в
точке х0:
у
lim
y
x 0 х
Производная – это скорость
изменения функции!
Штрих обозначает
действие
нахождения
производной
3.
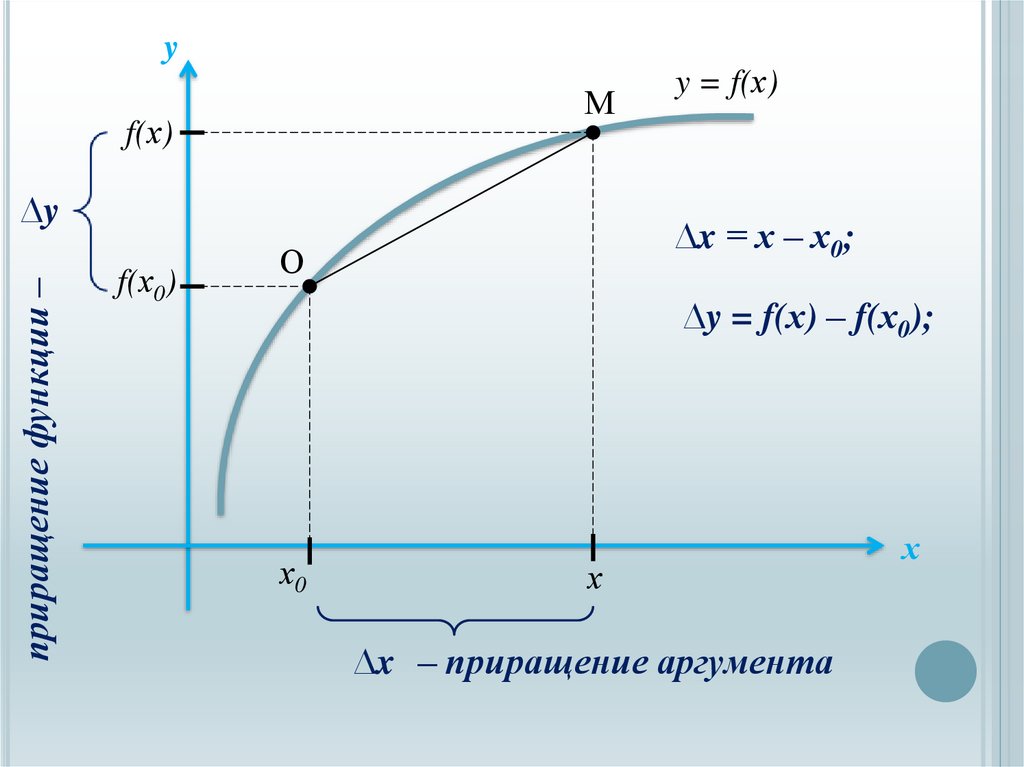
yМ
f(х)
приращение функции –
∆y
f(х0)
y = f(х)
∆x = х – х0;
О
∆y = f(х) – f(х0);
х0
х
∆x – приращение аргумента
х
4.
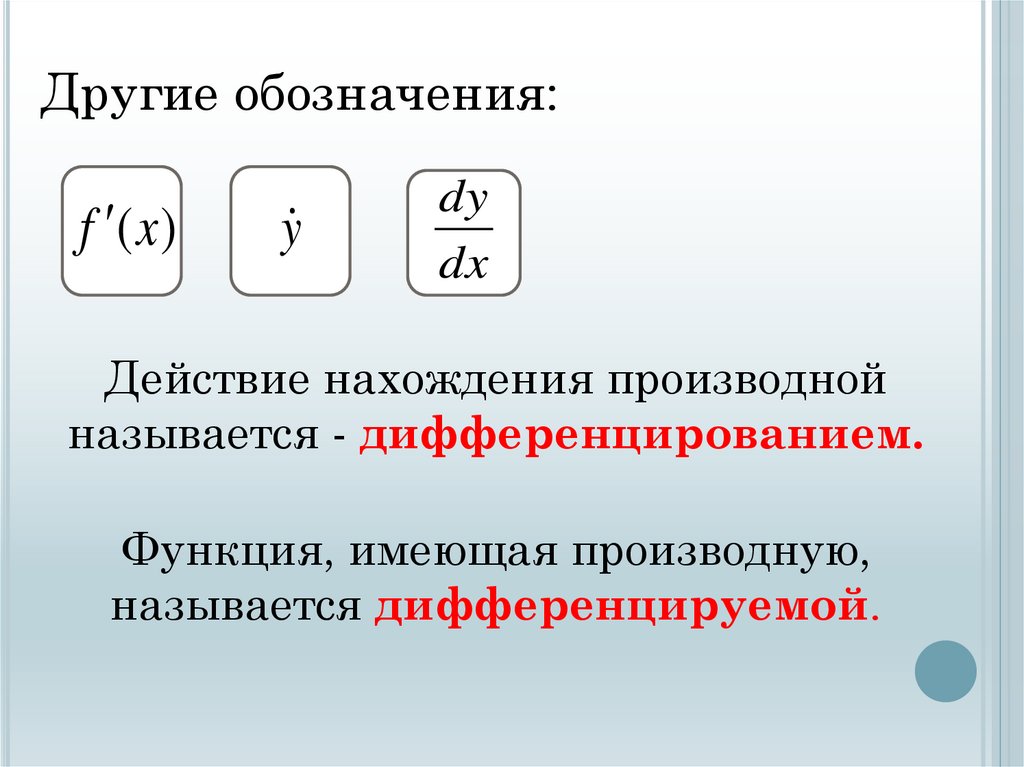
Другие обозначения:f (x )
y
dy
dx
Действие нахождения производной
называется - дифференцированием.
Функция, имеющая производную,
называется дифференцируемой.
5.
ОБЩЕЕ ПРАВИЛО ВЫЧИСЛЕНИЯ ПРОИЗВОДНОЙ:1) y y f ( x x)
2) y f ( x x) f ( x)
y f ( x x) f ( x)
3)
x
x
y
4) y lim
x 0 x
6.
Правила дифференцированияU V W U V W
С U С U
U V U V V U
U V W U V W V U W W U V
U U V U V
2
V
V
U 1
U
С С
С
С
V
2
V
V
7.
Производные элементарных функций1)
С 0 , С постоянная
2)
x 1
x n x
1
4) х
2 x
3)
5)
n
n 1
1
1
2
x
x
СТЕПЕННЫЕ
ФУНКЦИИ
8.
Производные элементарных функцийa a lna
7) e e lne e
6)
x
x
x
8)
x
x
ПОКАЗАТЕЛЬНЫЕ
ФУНКЦИИ
1
log a x
х lna
1
9) lnx
х
0,4343
10) lgx
х
ЛОГАРИФМИЧЕСКИЕ
ФУНКЦИИ
9.
Производные элементарных функций11)
12)
sinx cosx
cosx sinx
13)
1
tgx
2
cos x
14)
1
ctgx 2
sin x
ТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
10.
Математический диктантx
С U
С
1
x
cosx
n
x
e
x
sinx
U V
lnx
tgx
a
x
U V
ctgx
х
U
V
11.
Вычисление производных элементарных функций1) y x
3 x
y x
3
3) y x
3 1
3x
2
7
y 7x
2, 4
y 2,4 x
5
y 5 x
2) y x
4) y x
x n x
n
3
6
1, 4
6
n 1
12.
Вычисление производных элементарных функцийa x a n x
n
5 ) y 4х 2 2x 3 3x 10
4
6) y 3х 6 x
0,5
0,008
С 0
U V U V
7 ) y 3х 1,5x 7x 0,35
4
2
x0 2
8) y
n 1
1
5
x х x , x0 1
x
13.
Вычисление производных элементарных функцийU V U V
9 ) y 2 tgx 5 lnx 4 x
10 ) y 8 ctgx 2 cosx 7 lg x 0,136
2
11 ) y 2 log 2 x 3 x 10 x
3
3
4
12) y 3 cos x 4 sin х 2e x 5x, x0 0
14.
Д/З Выучить формулы!Вычислить производные:
1) y 1,2x 4х 3x 1,2х 0,007
5
2
3
2) y lgx 3 ctgx 9 6 lnx
x
3) y 5x 2x 3x 2x
2
2
Вычислить производные в заданных точках:
4) y 7x 13х 5x 3, x0 6,5
3
3
2
5) y 4x 1,5x 9х
x0 1,4
2
2
3
15.
Вычисление по правилу произведенияU V U V U V
1) у = x∙sinx;
у′ = (x∙sinx)′ = (x)′∙sinx + x∙(sinx)′ =
U
V
= 1∙sinx + x∙cosx = sinx + x∙cosx
16.
2) y x ey x e
x
U V U V U V
x
x e x e
x
x
1 e x e e 1 x
x
x
x
3) y x 3x 2 x 8
2
2
3
3
y x 3 x 2 x 8 2 x 8 x 3 x
2
3
2 x 3 2 x3 8 6 x 2 0 x 2 3x
4 x 4 16 x 6 x 3 24 6 x 4 18 x 3
10 x 4 24 x 3 16 x 24
17.
4) y' (4) y' (1) ?y 1 2 x x
U V U V U V
y 1 2 x x x 1 2 x
1 2x
1
0 2 x
1 2 x 2 x
2 x
2 x
7
1 2 4
5,75
4
y ' ( 4) 2 4
4
2 4
1
1 2 1
2,5
2
y ' (1) 2 1
2
2 1
y ' (4) y ' (1) 5,75 2,5 3,25
18.
5) 1 2 x x 1 2 x x x 1 2 x3
3
3
1
3
0 2 3x x
1 2x
2 x
3
1 2x
2
6 x x
2 x
3
1 2 1
2
y ' (1) y (1) 6 1 1
1 2 13 1
2 1
2
1
6
1 5,5
2
19.
Вычисление по правилу дроби1 2х
1) у
;
3 5х
U U V UV
2
V
V
1 2х
1 2 х 3 5 х 1 2 х 3 5 х
у
2
3 5х
3 5х
2 3 5 х 1 2 х 5 6 10 х 5 10 х
11
2
2
2
3 5 х
3 5 х
3 5 х
20.
2)1 sin x
у
;
1 sin x
U U V UV
2
V
V
1 sin x 1 sin x 1 sin x 1 sin x 1 sin x
у
2
1 sin x
1 sin x
cos x 1 sin x 1 sin x cos x
2
1 sin x
2 cos x
cos x cos x sin x cos x sin x cos x
2
2
1 sin x
1 sin x
21.
Вычислить производную в заданной точке:3)
2 3х
у
1 2х
2
2 3x
у
1 2x
2
x0 1
2 3x 1 2x 2 3x 1 2x
2
2
1 2 x
2
2
2
6
x
12
x
4
6
x
6 x 1 2 x 2 3x 2
2
2
1 2 x
1 2 x
2
6x 6x 4
2
1 2 x
2
6 6 4
y ( 1)
4
2
1 2
22.
е ху
2х
х
4)
U U V UV
2
V
V
2
x
2
x
2
е х
e x 2 х e x 2 х
у
2
2 х
2х
х
2
e 2 x 2 x e x 2
2x e 4x 2 e 2x
x
x
4x2
2 x e x 2e x 2 x 2
2
4x
2
x
2
4x2
x ex ex x2
2
2x
x
2
23.
U U V UV2
V
V
6 x 3 ln x
5) у
;
2
2 x
2
2
6 x 3 ln x 6 x 3 ln x 2 x 6 x 3 ln x 2 x
у
2
2
2 x
2 x2
3
2
6
2
x
6 x 3 ln x 2 x
x
2
2 x2
6
6
2
2
12 6 x 3x 12 x 6 x ln x 6 x ln x 6 x 3x 12
x
x
2 2
2 2
2 x
2 x
2
24.
Самостоятельно вычислить производную в заданной точке:y (25) y 4 ?
y
(
0
)
?
2) y 4 x х x 2e
y (0) ?
3) y 2 x 8e cos x
1) y 3 x x
2
2
3
x
x
2 4х
4) у
2 х
9 ln х 4 x
5) у
2
2х
3
y ( 6) ?
y (1) ?
25.
Производная сложной функцииf(x) = f ( u(x) )
f′(x) = f′(u) ∙ u’
Пример:
1) у = (2x – 7)14;
u
u(x) = 2x – 7;
f(u) = u14;
у′ = f′(u) ∙ u′(x) = 14u13 ∙ 2 = 28(2x – 7)13
26.
3) у 3 5 x5
4) у
;
3
f(x) = f ( u(x) )
f′(x) = f′(u) ∙ u′(x)
10
7 x 2
5) у 2 х 3;
6
10 ) у e
*
6) у e
2 x 15
7) у ln x x 9
3
8) у sin 2 x
2
2
9 ) у 3 sin x 3
*
3 2 x 4
2
1
27.
Производная второго порядкаПроизводной второго порядка (второй
производной) называется производная от первой
производной.
у ( x) у
Производная 3-го порядка:
у (x)
Производная 4-го порядка:
у ( x)
( 4)
28.
Вычислить:1) y 4 x 2 x 7 x 15,9; y
5
3
2) y 3x 5 sin x e 2 ln x; y
4
x
3) y 3x 6 x 17 x 7 , y 2
6
2
4) y 9 x 8 cos x 4e 2019
4
x
y 0 , y 0 , y 0 , y 0
29.
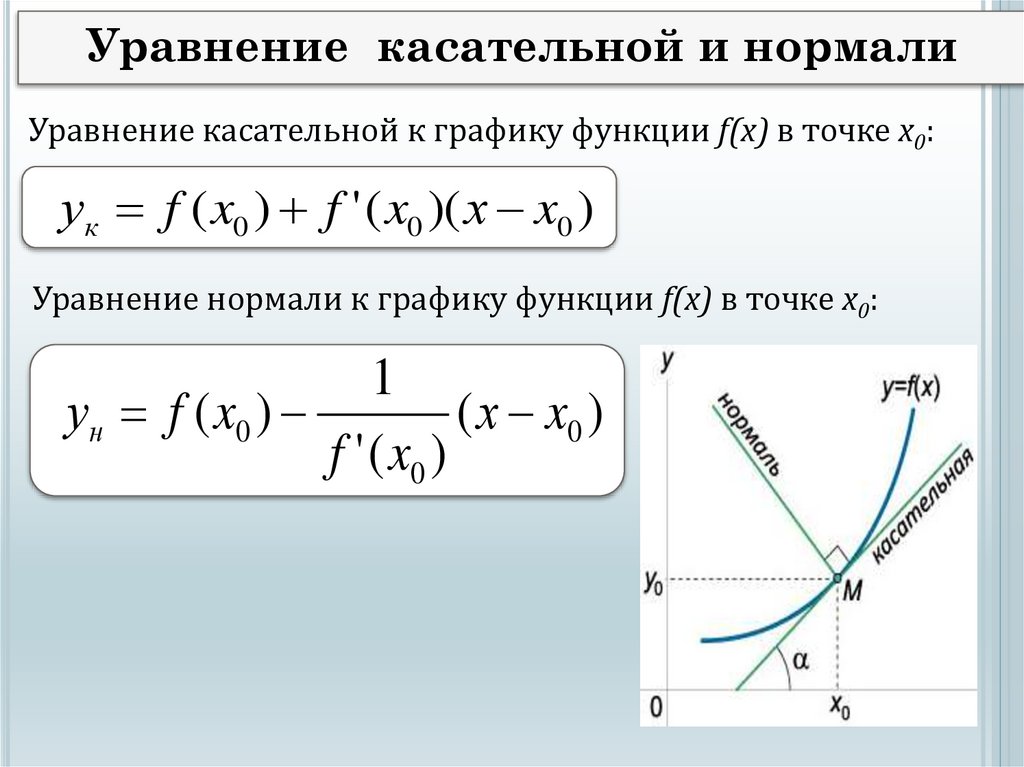
Уравнение касательной и нормалиУравнение касательной к графику функции f(x) в точке х0:
ук f ( x0 ) f ' ( x0 )( х x0 )
Уравнение нормали к графику функции f(x) в точке х0:
1
ун f ( x0 )
( х x0 )
f ' ( x0 )
30.
№3Составить уравнение касательной и нормали
к графику функции в заданной точке:
f ( x) x 2 4, x0 3
Решение:
1) f(х0) = 32 – 4 = 5;
2) f ′(х) = 2x ;
3) f ′(х0) = 2∙3 = 6;
4) ук 5 6 ( х 3)
ук 6 х 13
1
5) ун 5 ( х 3)
6
1
1
ун x 5
6
2
31.
№4Составить уравнение касательной и нормали
к графику функции в заданной точке:
f ( x) 4 x x , x0 3
2
Решение:
1) f ( 3) 4 3 9 2
2) f 1 2 x
3) f ( 3) 1 6 5
4) укас 2 5 ( х 3) 2 5x 15 5x 13
1
1
3
1
3
5) унорм 2 ( х 3) 2 x x 2
5
5
5
5
5
32.
№5Найти угловой коэффициент и угол наклона
касательной. Составить уравнение касательной
к графику функции:
f ( x) 2 x 3x 4 12, x0 2
Решение: 1)
f ( 2) 4 48 12 40
2) f 2 12 x3
3) f ( 2) 2 96 98 , k 98
4) arctg 98 89 24 55
5) ук 40 98 ( х 2) 98x 156
33.
Монотонность функции и точкиэкстремума
Рассмотрим функцию f(x). Найдем f ′(x).
Если на некотором интервале
f ′(x) > 0, то f(x) возрастает.
f ′(x) < 0, то f(x) убывает.
Точки, в которых f ′(x) = 0 или не существует, называются
критическими точками.
f ′(x0) = 0 → x0 – критическая точка
Эти точки могут быть точками экстремума (максимум или
минимум).
34.
–+
х0
f ′(х)
х
f (х)
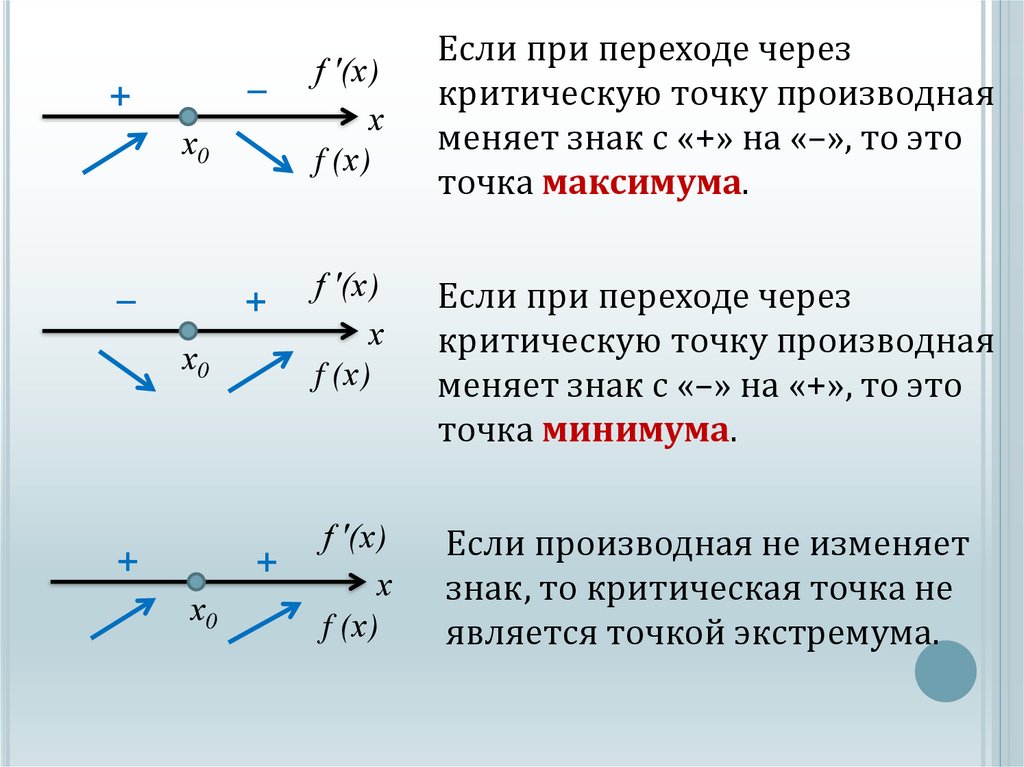
Если при переходе через
критическую точку производная
меняет знак с «+» на «–», то это
точка максимума.
х0
f ′(х)
х
f (х)
Если при переходе через
критическую точку производная
меняет знак с «–» на «+», то это
точка минимума.
х0
f ′(х)
х
f (х)
Если производная не изменяет
знак, то критическая точка не
является точкой экстремума.
–
+
+
+
35.
Правило исследования функциина монотонность и экстремум
1. Найти производную функции f ′(x);
2. Найти критические точки (f ′(x)=0 или
не существует);
3. Исследовать знак производной на
промежутках, определить точки
максимума, минимума и промежутки
монотонности;
4. Вычислить значения функции в
точках экстремума
36.
№ 1 Найти промежутки монотонности и точкиэкстремума функции: f ( x) 7 x 10
f ( x ) 7
7 0 критических точек нет экстремума нет
+
f′
х
f
Ответ : функция возрастает при x R
точек экстремума нет
37.
№ 2 Найти промежутки монотонности 2и точкиэкстремума функции: f(x) 2x 4х 9
f (x) 4х 4
4х 4 0
4х 4
x 1
+ max _
1
ymax f(1) 2 12 4 1 9 2 4 9 7
Ответ: функция возрастает при x ;1
функция убывает при x 1;
1; 7 т. максимума
f′
х
f
38.
и точки№ 3 Найти промежутки монотонности
экстремума функции: f ( x) x 3 6 x 2 9 х 8
f ( x) 3x 2 12 х 9
3 x 2 12 х 9 0
x 4х 3 0
2
x1 x2 4
x1 3 x2 1
x1 x2 3
+ max – min +
-3
-1
f′
х
f
ymax f ( 3) 3 6 3 9 3 8 8
3
2
ymin f ( 1) 1 6 1 9 1 8 12
3
2
Ответ : функция возрастает при x ; 3 1;
функция убывает при x 3; 1
3; 8 т. максимума 1; 12 т. минимума
39.
№ 4 Найти промежутки монотонности4 и точкиэкстремума функции: f ( x) 2 x 8 x 3 5
f ( x) 8x3 24 х 2
8 x 3 24 х 2 0
x 3х 0
3
2
x 2 ( x 3) 0
x1 0 x2 3
–
–
0
min
3
ymin f (3) 2 34 8 33 5 49
Ответ : функция возрастает при x 3;
функция убывает при x ;0 0;3
3; 49 т.минимума
+
f′
х
f
40.
Д/ЗНайти промежутки монотонности и
точки экстремума функции:
1) f(x) x 3х 2
2
2) f(x) x 3x 9х 1
3
2
3) f(x) x 8х
4
2
4) f(x) x 4x 9
4
3
41.
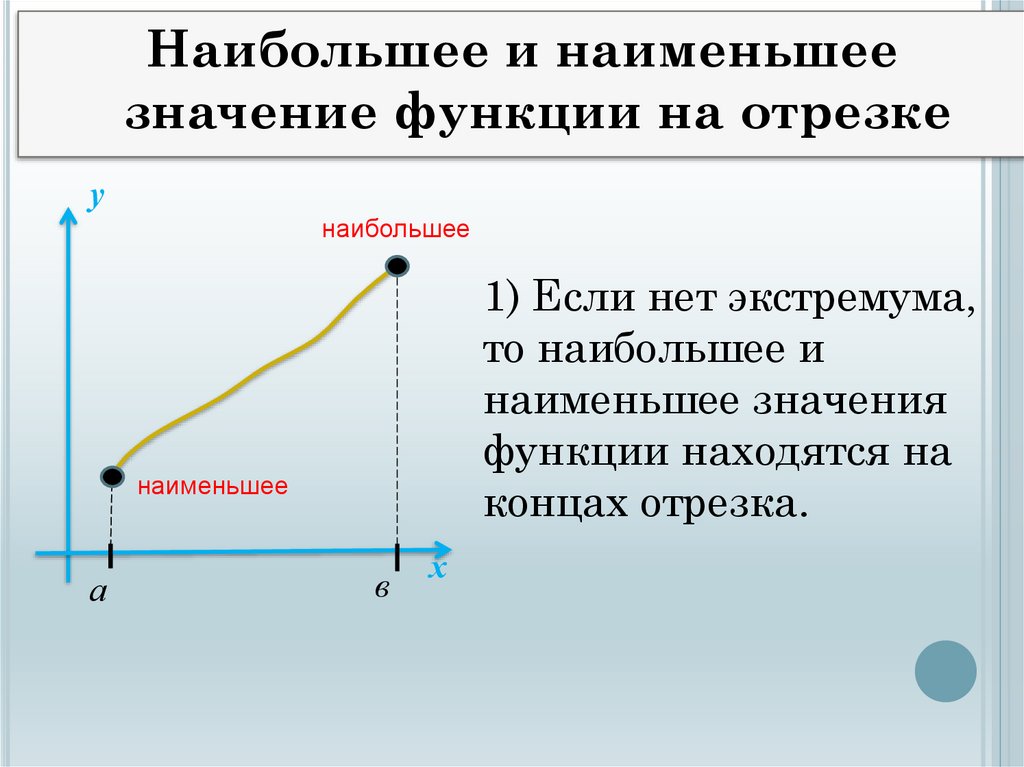
Наибольшее и наименьшеезначение функции на отрезке
у
наибольшее
1) Если нет экстремума,
то наибольшее и
наименьшее значения
функции находятся на
концах отрезка.
наименьшее
а
в
х
42.
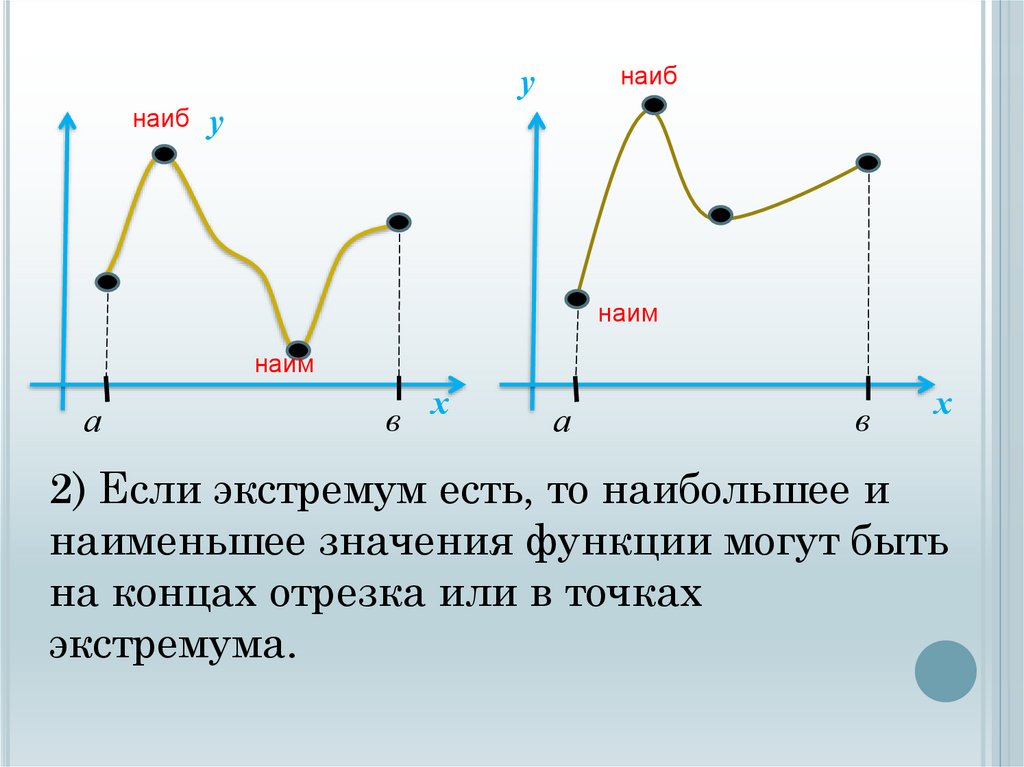
наибу
наиб
у
наим
наим
а
в х
а
в
х
2) Если экстремум есть, то наибольшее и
наименьшее значения функции могут быть
на концах отрезка или в точках
экстремума.
43.
Правило нахождения наибольшегои наименьшего значения функции
1. Найти производную функции f ′(x);
2. Найти критические точки (f ′(x)=0), проверить
принадлежат ли они заданному промежутку;
3. Вычислить значения функции в точках,
которые принадлежат промежутку;
4. Вычислить значения функции на концах
промежутка (f(a) и f(b));
5. Сравнить полученные значения, выбрать
наибольшее и наименьшее значение
функции, записать ответ.
44.
№1Найти наибольшее и наименьшее значения
функции на отрезке: f ( x) x3 1,5х 2 6 х 1, 2;0
Решение:
f ( x) 3x 3х 6;
x x 1
2
2
3x 3х 6 0; x х 2 0; x x 2
х1 1; х2 2. 1 2;0 ; 2 2;0 .
3
2
f ( 1) ( 1) 1,5( 1) 6( 1) 1 4,5
3
2
f ( 2) ( 2) 1,5( 2) 6( 2) 1 1
3
2
f (0) 0 1,5 0 6 0 1 1
2
1
1
наибольшее : f ( 1) 4,5
2
2
наименьшее : f ( 2) 1
45.
№ 2 Найти наибольшее и наименьшеезначения функции:
f ( x) x 7 х 11х 21 на отрезке [-1; 0].
3
2
f ( x) 3x 14 х 11
2
3 x 14 х 11 0
2
2
1 1;0 3 1;0
х1 1; х2 3
3
3
2
f ( 1) ( 1) 7( 1) 11( 1) 21 40
3
2
f (0) 0 7 0 11 0 21 21
3
2
f ( 1) 40 наименьшее
f (0) 21 наибольшее
46.
№3Найти наибольшее и наименьшее
значения функции:
3
2
f ( x) x 3х 9 х 35 на отрезке [-4; 4]
f ( x) 3x 6 х 9
2
3x 2 6 х 9 0; х1 1; х2 3
1 4;4 3 4;4
3
2
f ( 1) ( 1) 3( 1) 9( 1) 35 40 наибольшее
f (3) 3 3 3 9 3 35 8
3
2
f ( 4) ( 4) 3( 4) 9( 4) 35 41 наименьшее
3
2
f (4) 43 3 42 9 4 35 15
47.
№4Найти наибольшее и наименьшее
значения функции:
1 2 1 3
f ( x) x х
2
3
на отрезке [1; 3].
2
f ( x) x x
2
x x 0; х1 0; х2 1 0 1;3 ; 1 1;3 .
1 2 1 3 1 1 1
наибольшее
f (1) 1 1
2
3
2 3 6
1 2 1 3 9 27
f (3) 3 3
4,5 9 4,5 наименьшее
2
3
2 3
48.
ИССЛЕДОВАНИЕФУНКЦИИ С ПОМОЩЬЮ
ПРОИЗВОДНОЙ И
ПОСТРОЕНИЕ ЕЕ
ГРАФИКА
49.
ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ1) Найти область определения функции;
2) Найти точки пересечения графика с осями координат;
3) Найти промежутки монотонности функции и её
экстремумы;
4) Найти промежутки выпуклости графика функции и точки
перегиба;
5) Заполнить таблицу дополнительных значений;
6) Построить график функции, используя полученные
результаты исследования.
50.
ЗАДАНИЕ: ИССЛЕДОВАТЬ ФУНКЦИЮ С ПОМОЩЬЮ ПРОИЗВОДНОЙИ ПОСТРОИТЬ ЕЁ ГРАФИК
y x 6 x 11x 6
3
2
Решение:
1) Область определения функции: x R
2) При пересечении с осью OY: x 0
y 0 6 0 11 0 6 6
3
2
0; 6
При пересечении с осью OX:
y 0
1;0 , 2;0 , 3;0
http://planetcalc.ru
51. Исследование функции с помощью производной и построение ее графика
3) Найти промежутки монотонности и точкиэкстремума функции: y x 3 6 x 2 11x 6
f ( x) 3x 2 12 х 11
3 x 2 12 х 11 0
12 144 4 3 11 12 12
x1, 2
2 3
6
+
x1 2,58 x2 1,42
max
1,42
–
min
+
2,58
f′
х
f
ymin f (2,58) 2,58 6 2,58 11 2,58 6 0,38
3
2
ymax f (1,42) 1,42 6 1,42 11 1,42 6 0,38
3
2,58; 0,38 минимум
2
1,42;0,38 максимум
52. Общая схема исследования
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯИССЛЕДОВАТЬ ФУНКЦИЮ С ПОМОЩЬЮ ПРОИЗВОДНОЙ И
ПОСТРОИТЬ ЕЁ ГРАФИК
f ( x) x 3x 4
3
2
53. Задание: Исследовать функцию с помощью производной и построить её график
Подготовка к контрольной работе1) Найти чему равна производная:
4
y 7 2e 5 cos x
x
4
x
y 2e 2 5 sin x
x
x
8
y 10 sin x 4 6 ln x
x
x
y 9 x 7 4ctgx 5 x 6 x
y ?
y ?
54.
Подготовка к контрольной работе2) Найти чему равна производная функции в заданной точке:
y 2 x 5x 13x 8, y ( 3) ?
3
2
2
y 6 x 10 x 13
y ( 3) 6 9 10 3 13 97
y 4 x x 6 x 3, y (5) ?
3
y ?
y (5) ?
2
55. Задание для самостоятельного решения Исследовать функцию с помощью производной и построить её график
Подготовка к контрольной работе3) Дан закон движения материальной точки, найти
скорость и ускорение за время t:
S 15t 3 18t 2 9t 1,
S t 3 3t 2 7t 3,
t 1c.
t 2c.
v 45t 36t 9
a 90t 36
v(1) 72( м / с)
a ?
a (1) 126( м / с 2 )
a ( 2) ?
2
v ?
v(2) ?
56.
Подготовка к контрольной работе4) Составить уравнение касательной:
y 4 x 5x 6,
2
x0 4
y(4) 4 42 5 4 6 50
y 8 x 5
y x 3x 4, x0 2
2
y ( 2) ?
y ?
y (4) 8 4 5 27
y ( 2) ?
yкас 50 27 x 4
yкас ?
yкас 27 x 58
57.
Подготовка к контрольной работе5) Найти экстремумы функции:
y 2 x 9 x 12 x 18
3
2
y 6 x 2 18 x 12
– min
6 x 2 18 x 12 0
1
+
max
–
х
2
x 3x 2 0
ymin y(1) 2 13 9 12 12 1 18
x1 1, x2 2
ymin y(1) 13
ymax y (2) 2 23 9 2 2 12 2 18
2
ymax y(2) 14
Максимум : 2;14
Минимум : 1;13
58.
Подготовка к контрольной работе5) Найти экстремумы функции:
y x 9x 4
3
2
59.
Подготовка к контрольной работе6)Найти наибольшее и наименьшее значения функции на
отрезке:
4
y x 4 x 1, x 0;3
y 4 х 4
3
3
3
4 x 4 0; 4x 4; x 1; x 1
3
y(1) 14 4 1 1 2
y ( 0) 1
1 0;3
Наибольшее : y(3) 70
Наименьшее : y(1) 2
y(3) 3 4 3 1 70
4
60.
Подготовка к контрольной работе6)Найти наибольшее и наименьшее значения функции на
отрезке: y x 2 5 x 3, x 1;3







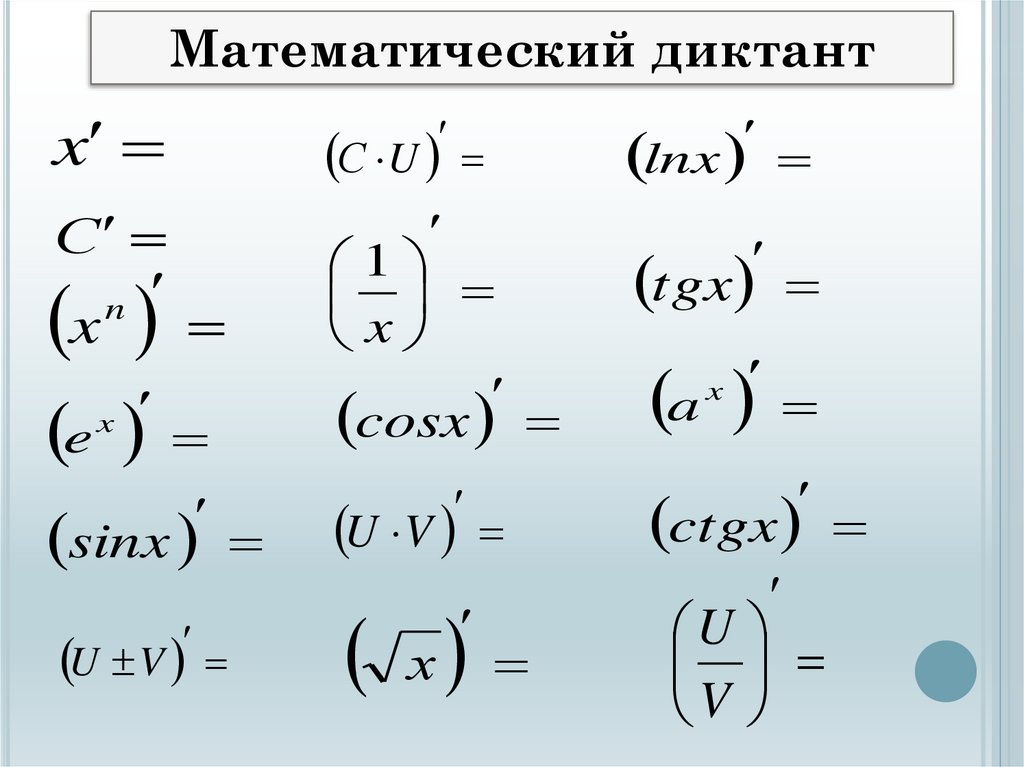






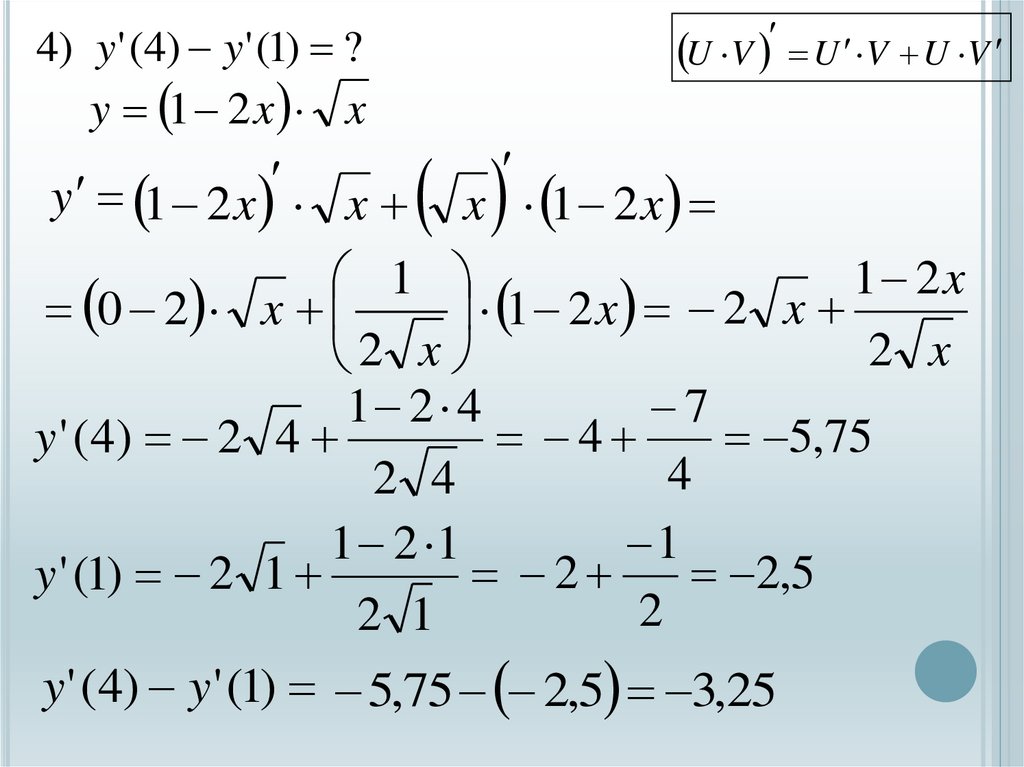
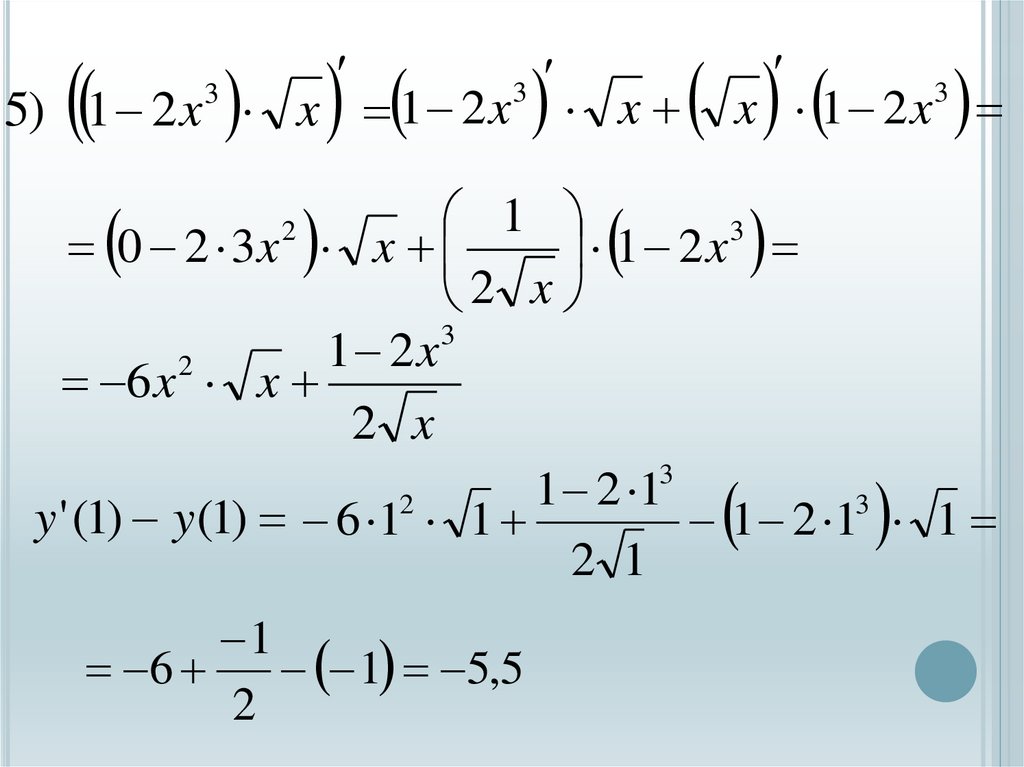

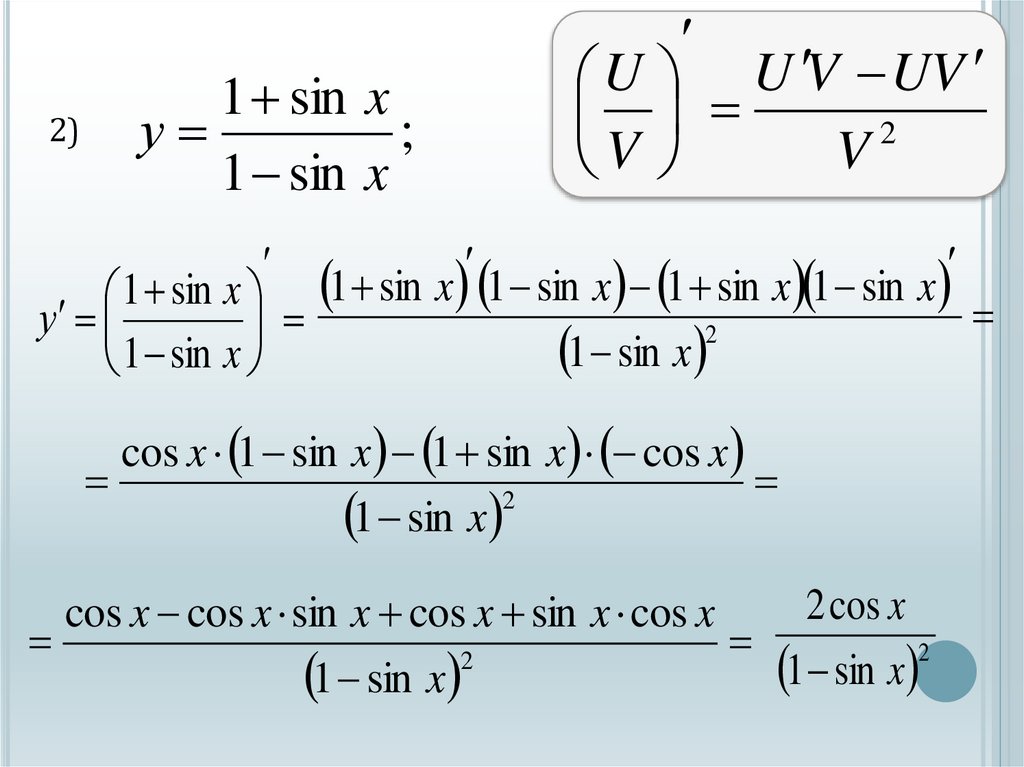

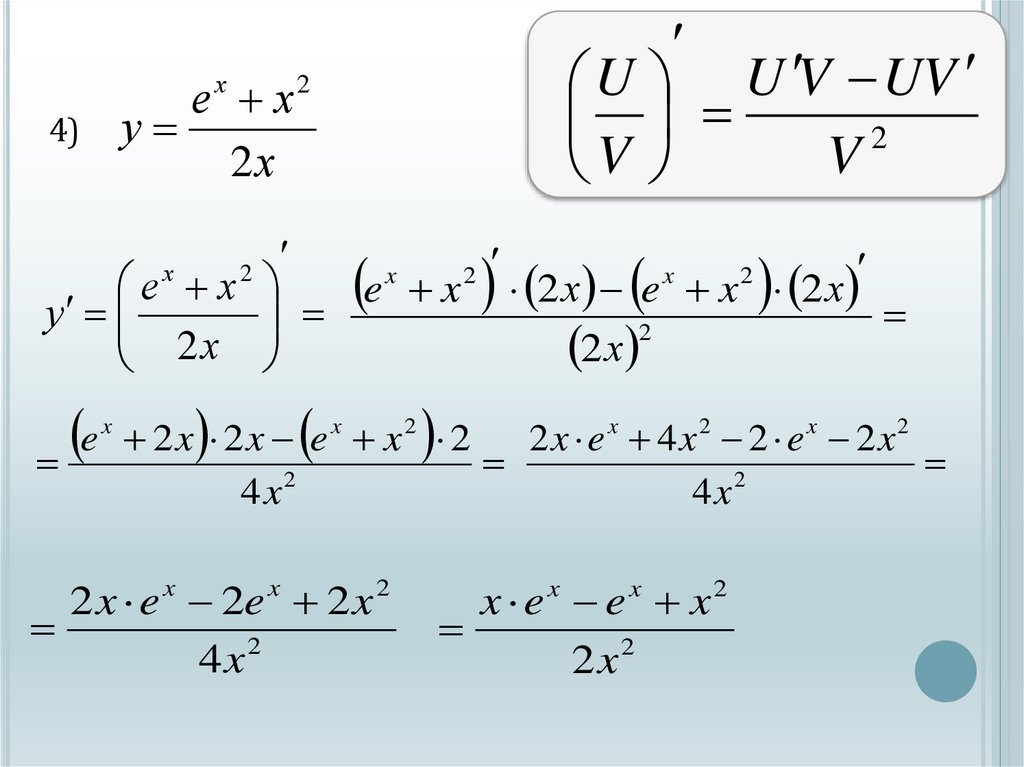
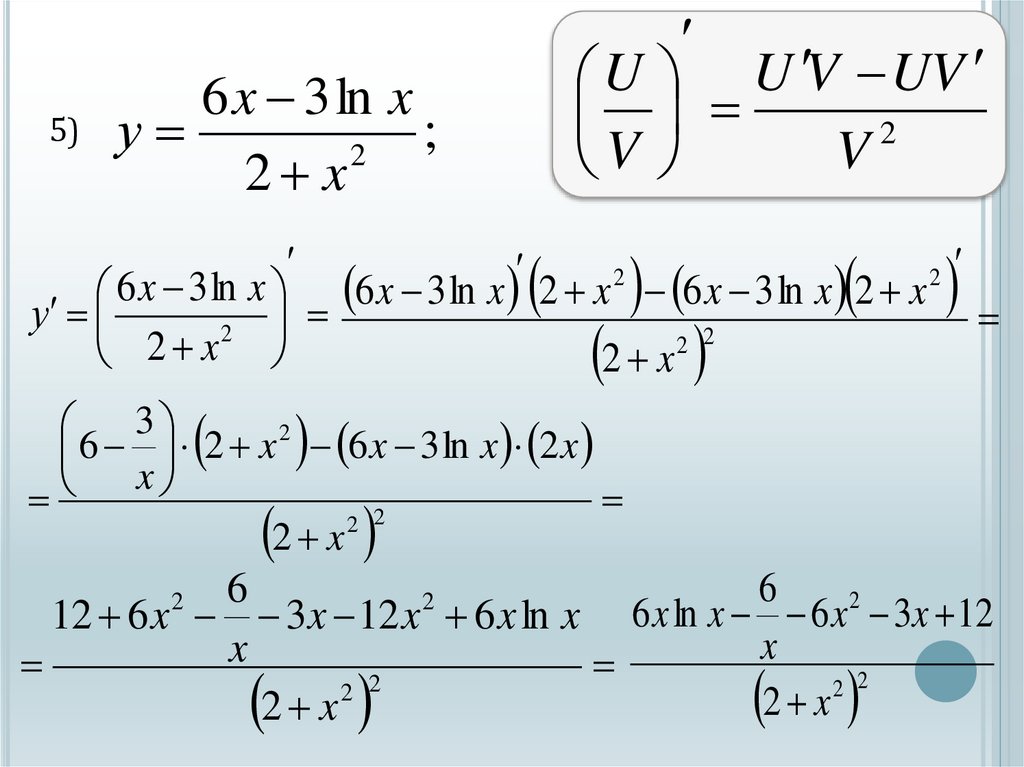


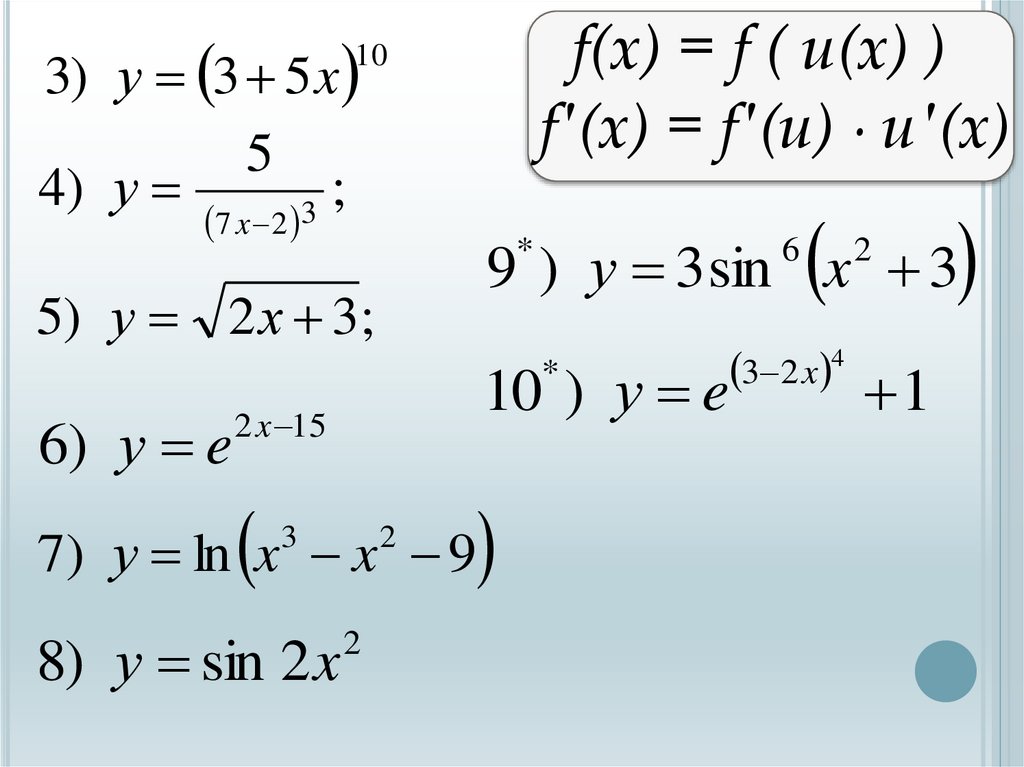






























 Математика
Математика








