3.5.0. Динамика МС Теорема мощностей (пример)

1.

Динамика
механической системы
Теорема мощностей
Саврасова Наталья Рэмовна
Слепова Светлана Владимировна
Игнатова Анастасия Валерьевна
Доценты кафедры «Техническая механика»

2.

Теорема мощностей
Алгоритм решения:
1. Выбрать объект, движение которого будет рассматриваться. Указать систему отсчета.
2. Указать активные силы.
3. Назвать связи и заменить внешние связи реакциями.
4. Выполнить кинематический анализ: решить задачу скоростей МС.
n
m
dT
5. Записать теорему мощностей
N ke N ij ,
dt k 1
j 1
6.
7.
8.
9.
Определить кинетическую энергию МС и ее производную.
Определить мощности всех внешних сил.
Составить уравнение движения и найти неизвестную величину.
* Если требуется определить какую-либо реакцию связей, то необходимо
рассмотреть движение одного из тел МС отдельно.
2

3.

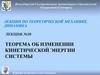
Теорема мощностей
Постановка задачи
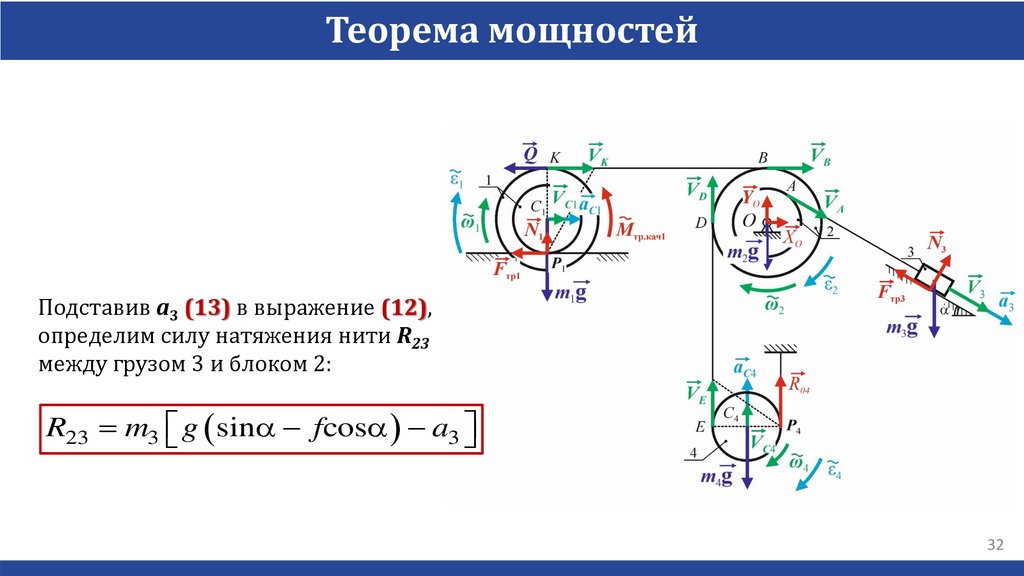
Найти ускорение груза a3 и силу натяжения троса R32 между грузом 3 и Блоком 2,
если заданы:
m1, m2, m3, m4 – массы тел механической системы, кг;
R1, r1, R2, r2, R4 – радиусы колеса 1 и блоков 2, 4, м;
ρ1, ρ2 – радиусы инерции колеса 1 и блока 2, м;
Q – сосредоточенная сила, Н;
a – угол наклона шероховатой поверхности;
f – коэффициент трения скольжения;
k – коэффициент трения качения, см.
Тросы невесомы и нерастяжимы.
Блок 4 считать однородными сплошными цилиндрами.
Учесть силу трения при скольжении груза и сопротивление качению блока по
шероховатой поверхности.
Проскальзыванием между телами и тросом, а также проскальзыванием при качении
колеса по поверхности пренебречь.
3

4.

Теорема мощностей
Дано:
m 1, m 2, m 3, m 4,
R1, r1, R2, r2, R4,
r 1, r 2,
Q,
f, k,
α.
Найти:
ускорение груза a3 и силу
натяжения троса R32
4

5.

Теорема мощностей
Решение
1. Рассмотрим движение МС,
состоящей из четырех тел, в ИСО.
2. Начальные условия:
t = 0: Vk(0) = 0, ∀k
Следовательно, МС движется ускоренно.
5

6.

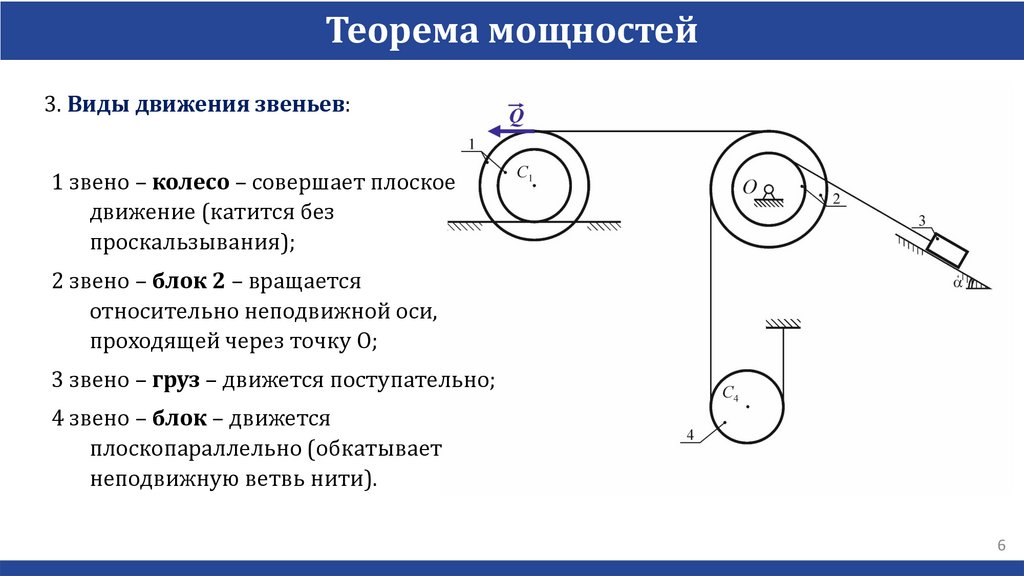
Теорема мощностей
3. Виды движения звеньев:
1 звено – колесо – совершает плоское
движение (катится без
проскальзывания);
2 звено – блок 2 – вращается
относительно неподвижной оси,
проходящей через точку O;
3 звено – груз – движется поступательно;
4 звено – блок – движется
плоскопараллельно (обкатывает
неподвижную ветвь нити).
6

7.

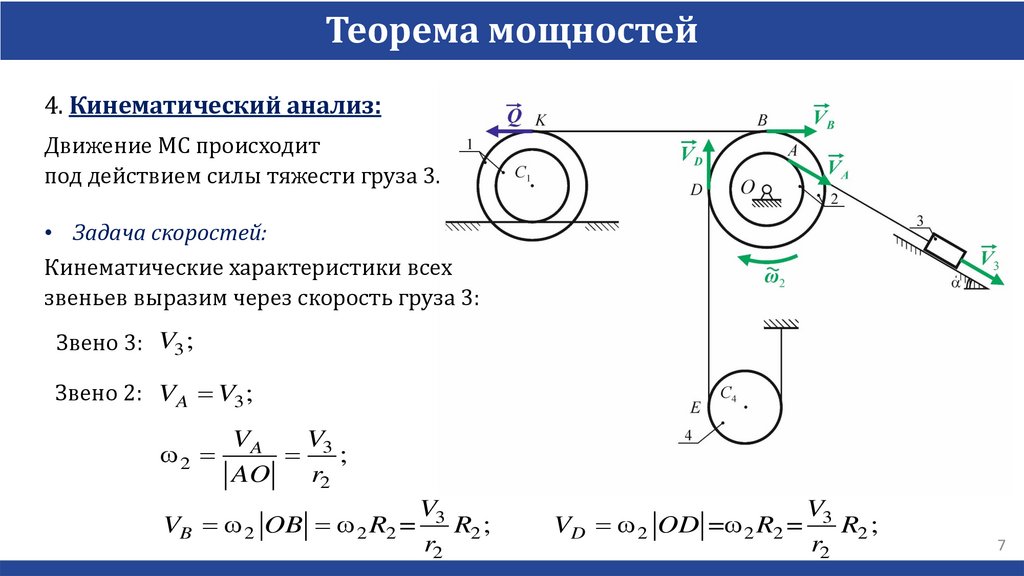
Теорема мощностей
4. Кинематический анализ:
Движение МС происходит
под действием силы тяжести груза 3.
• Задача скоростей:
Кинематические характеристики всех
звеньев выразим через скорость груза 3:
Звено 3: V3 ;
Звено 2: VA V3 ;
V3
VA
2
;
AO
r2
V3
VB 2 OB 2 R2 =
R2 ;
r2
V3
VD 2 OD = 2 R2 =
R2 ;
r2
7

8.

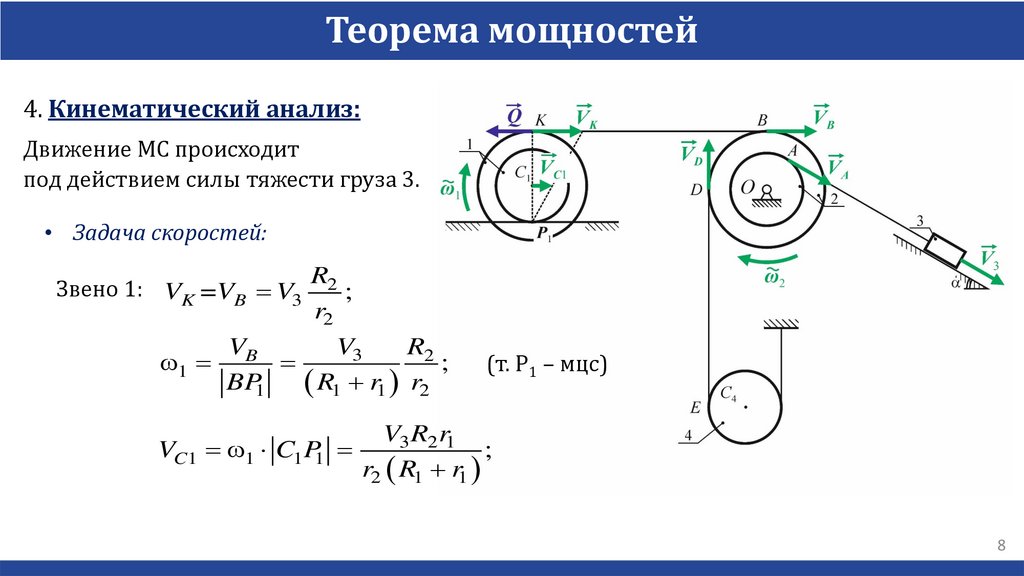
Теорема мощностей
4. Кинематический анализ:
Движение МС происходит
под действием силы тяжести груза 3.
• Задача скоростей:
R2
;
r2
V3
VB
R2
1
;
BP1
R1 r1 r2
Звено 1: VK =VB V3
(т. P1 – мцс)
V3 R2 r1
VC1 1 C1P1
;
r2 R1 r1
8

9.

Теорема мощностей
4. Кинематический анализ:
Движение МС происходит
под действием силы тяжести груза 3.
• Задача скоростей:
R2
;
Звено 4: VE =VD V3
r2
4
V R
VE
3 2 ; (т. P4 – мцс)
EP4
2r4 r2
V3 R2 r4 V3 R2
VC 4 4 C4 P4
=
;
r2 2r4
2r2
9

10.

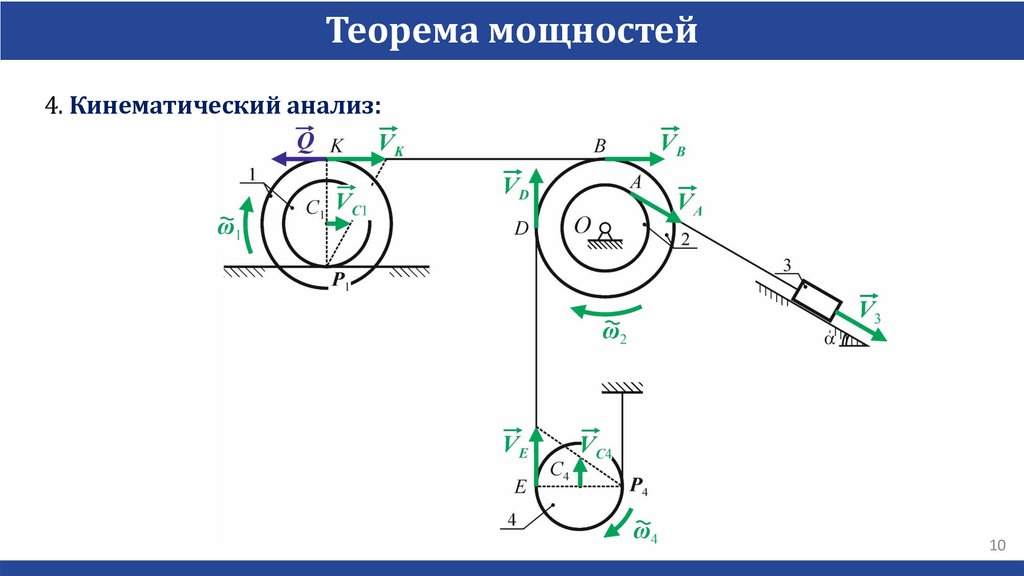
Теорема мощностей
4. Кинематический анализ:
10

11.

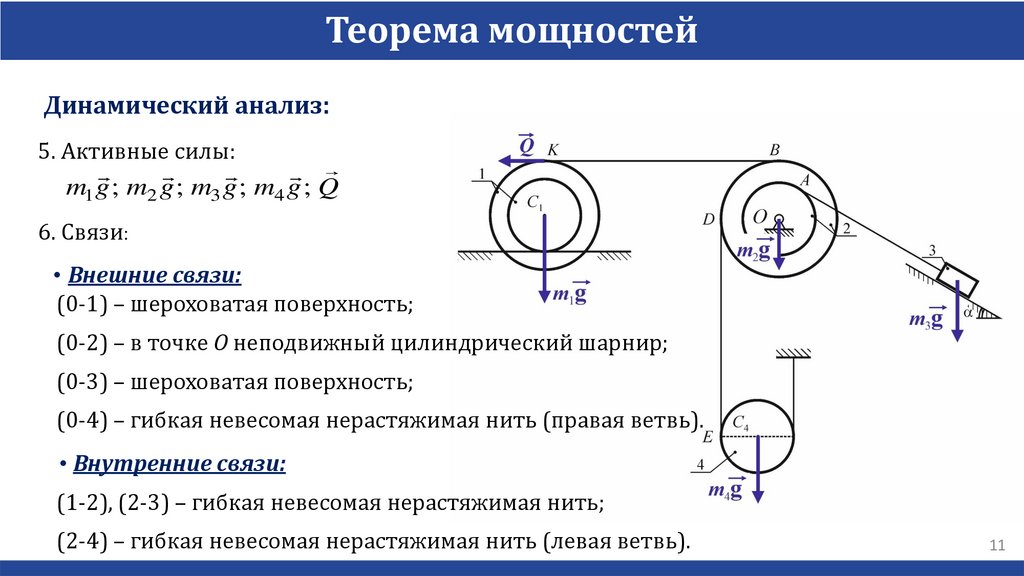
Теорема мощностей
Динамический анализ:
5. Активные силы:
m1 g ; m2 g ; m3 g ; m4 g ; Q
6. Связи:
• Внешние связи:
(0-1) – шероховатая поверхность;
(0-2) – в точке O неподвижный цилиндрический шарнир;
(0-3) – шероховатая поверхность;
(0-4) – гибкая невесомая нерастяжимая нить (правая ветвь).
• Внутренние связи:
(1-2), (2-3) – гибкая невесомая нерастяжимая нить;
(2-4) – гибкая невесомая нерастяжимая нить (левая ветвь).
11

12.

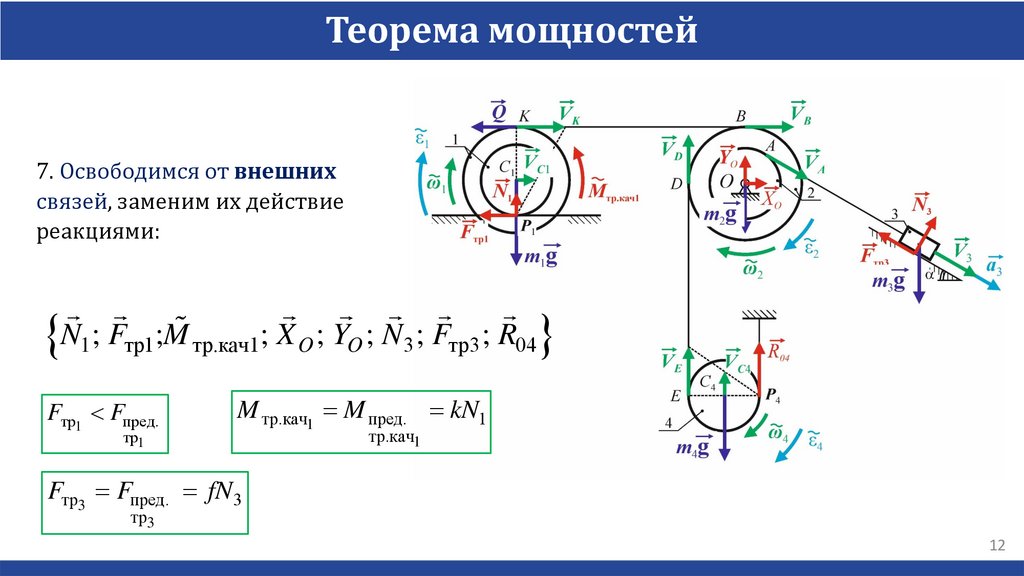
Теорема мощностей
7. Освободимся от внешних
связей, заменим их действие
реакциями:
N1; Fтр1;M тр.кач1; X O ; YO ; N3; Fтр3; R04
Fтр1 Fпред.
тр1
M тр.кач1 M пред. kN1
тр.кач1
Fтр3 Fпред. fN 3
тр3
12

13.

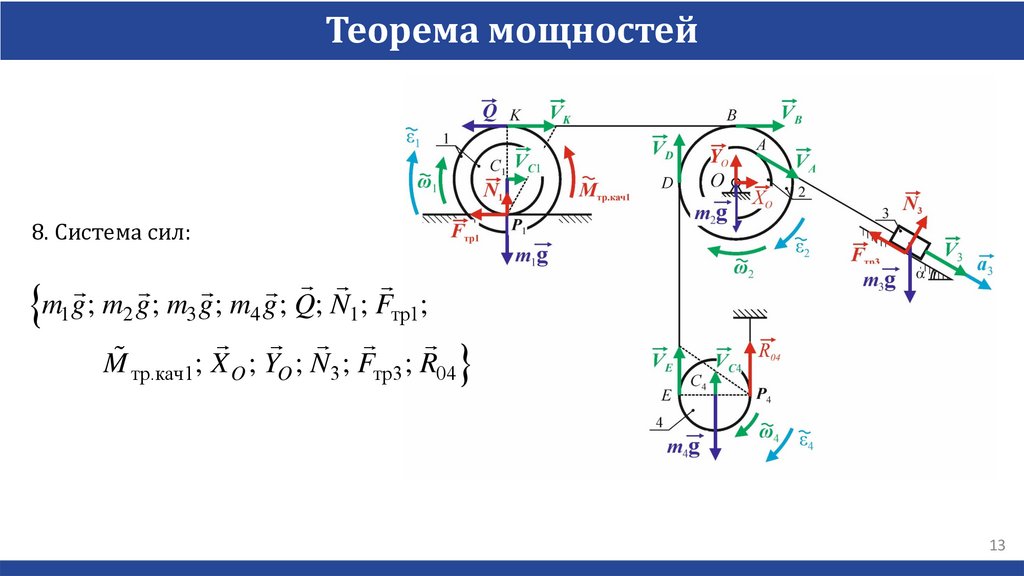
Теорема мощностей
8. Система сил:
m1g; m2 g; m3 g; m4 g; Q; N1; Fтр1;
M тр.кач1; X O ; YO ; N3 ; Fтр3 ; R04
13

14.

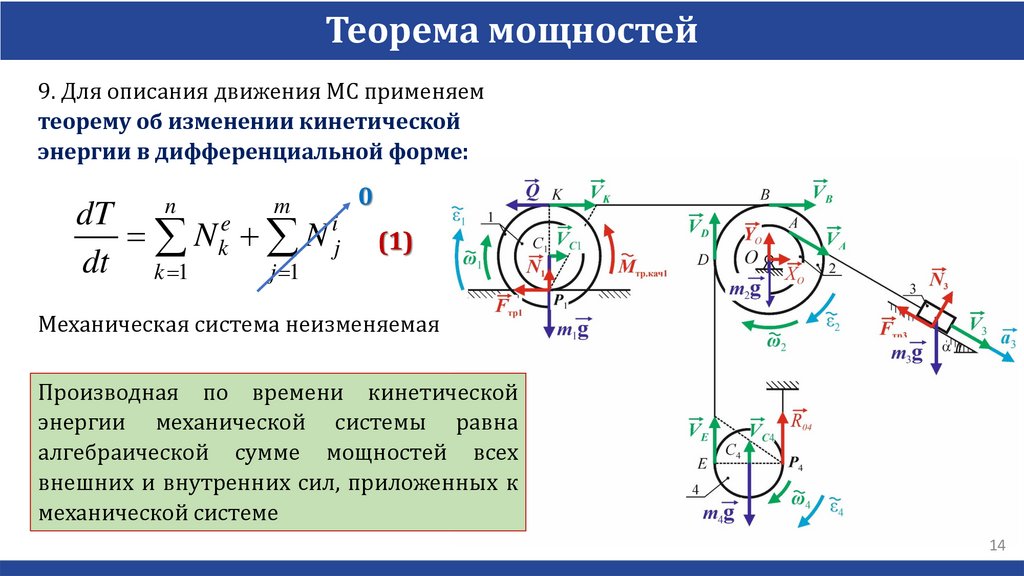
Теорема мощностей
9. Для описания движения МС применяем
теорему об изменении кинетической
энергии в дифференциальной форме:
n
m
dT
N ke N ij
dt k 1
j 1
0
(1)
Механическая система неизменяемая
Производная по времени кинетической
энергии механической системы равна
алгебраической сумме мощностей всех
внешних и внутренних сил, приложенных к
механической системе
14

15.

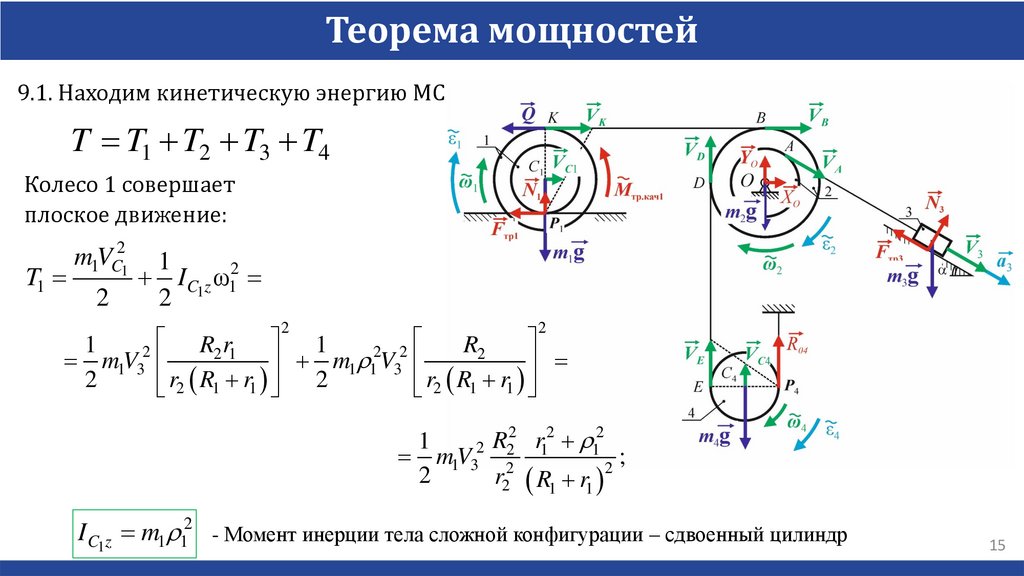
Теорема мощностей
9.1. Находим кинетическую энергию МС
T T1 T2 T3 T4
Колесо 1 совершает
плоское движение:
T1
m1VC21
2
1
I C1z ω12
2
2
2
R2 r1 1
R2
1
2
2 2
m1V3
m1r1 V3
2
r2 R1 r1 2
r2 R1 r1
2
2
2
R
r
r
1
1
m1V32 22 1
;
2
2
r2 R1 r1
I C1z m1r12 - Момент инерции тела сложной конфигурации – сдвоенный цилиндр
15

16.

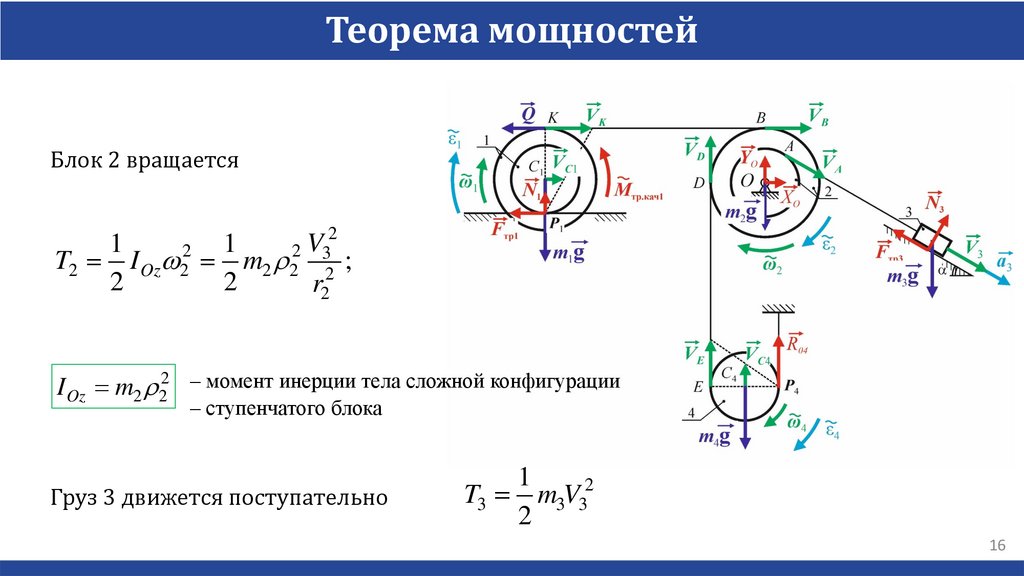
Теорема мощностей
Блок 2 вращается
2
V
1
1
T2 I Oz 22 m2 r 22 32 ;
2
2
r2
I Oz m2 r 22 – момент инерции тела сложной конфигурации
– ступенчатого блока
Груз 3 движется поступательно
1
T3 m3V32
2
16

17.

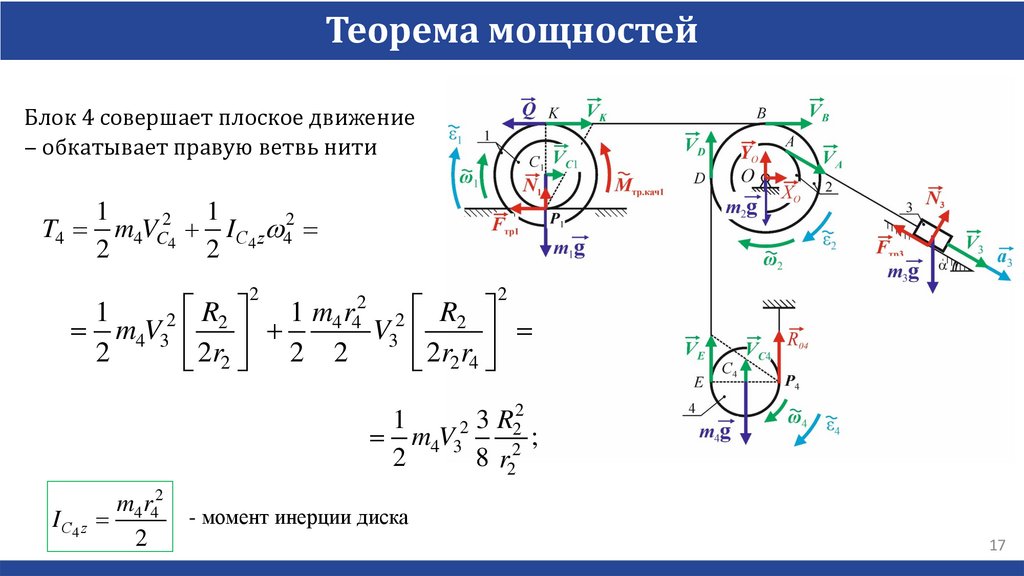
Теорема мощностей
Блок 4 совершает плоское движение
‒ обкатывает правую ветвь нити
1
1
2
T4 m4VC4 I С4 z 42
2
2
2
1
2 R2
m4V3
2
2r2 2
1 m4 r42
2
2
V3
2
R2
2r2 r4
2
R
1
3
2
m4V32
;
2
2
8 r2
m4 r42
I С4 z
2
- момент инерции диска
17

18.

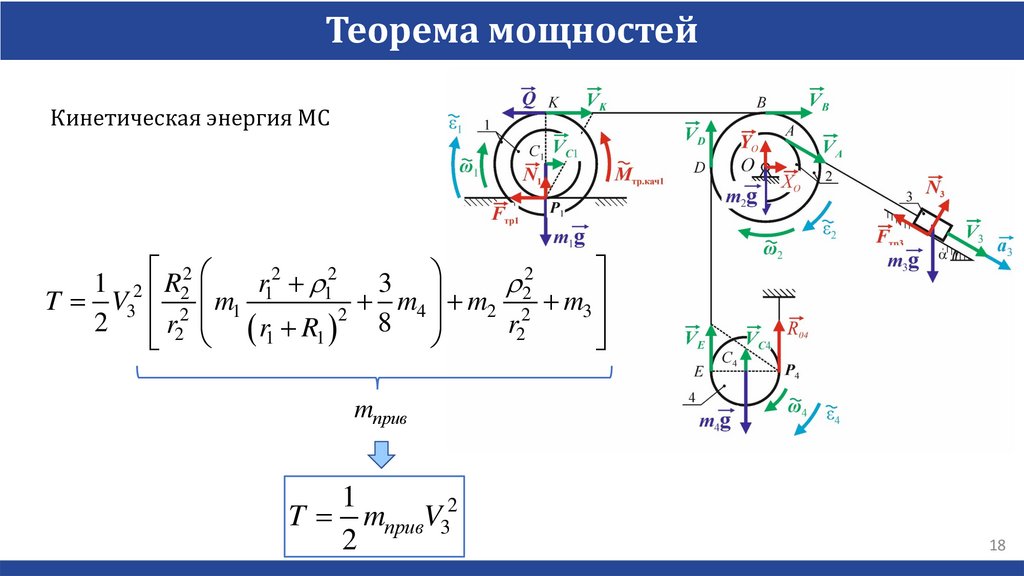
Теорема мощностей
Кинетическая энергия МС
r12 r12 3
r22
1 2 R22
T V3 2 m1
m4 m2 2 m3
2
2 r2 r1 R1 8
r2
mприв
1
2
T mпривV3
2
18

19.

Теорема мощностей
1
T mпривV32
2
Вычислим
dT dT dV3 dT
1
a3 mприв 2V3a3
dt dV3 dt
dV3
2
dT
mпривV3a3
dt
(2)
19

20.

Теорема мощностей
9.2. Вычислим мощности всех внешних сил
N F F V ,
где V ‒ cкорость точки
приложения силы F
N M M ω,
где ω ‒ угловая скорость тела,
к которому приложен момент M
20

21.

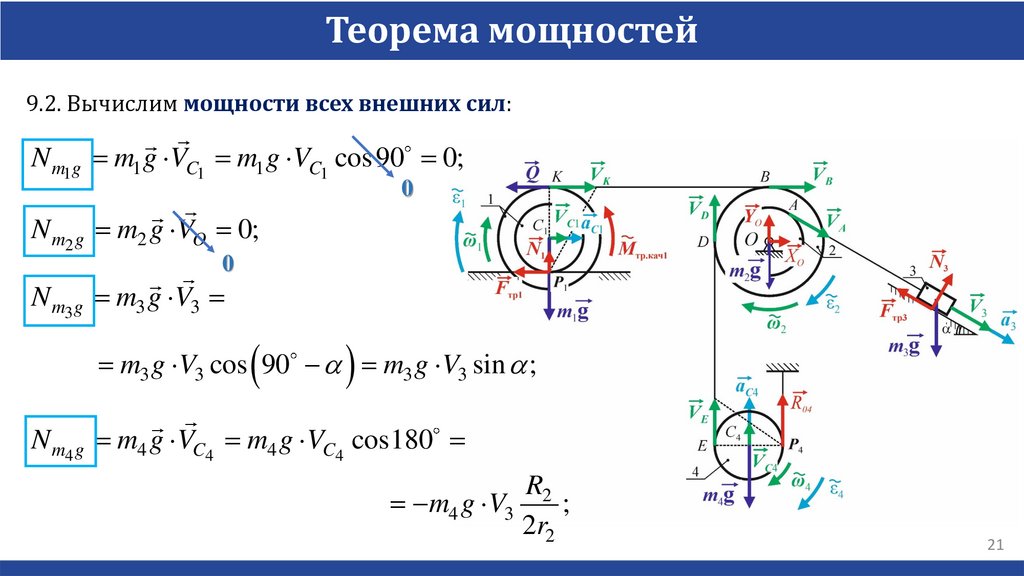
Теорема мощностей
9.2. Вычислим мощности всех внешних сил:
N m1g m1 g VC1 m1 g VC1 cos 90 0;
0
N m2 g m2 g VO 0;
0
N m3 g m3 g V3
m3 g V3 cos 90 a m3 g V3 sin a ;
N m4 g m4 g VC4 m4 g VC4 cos180
R2
m4 g V3
;
2r2
21

22.

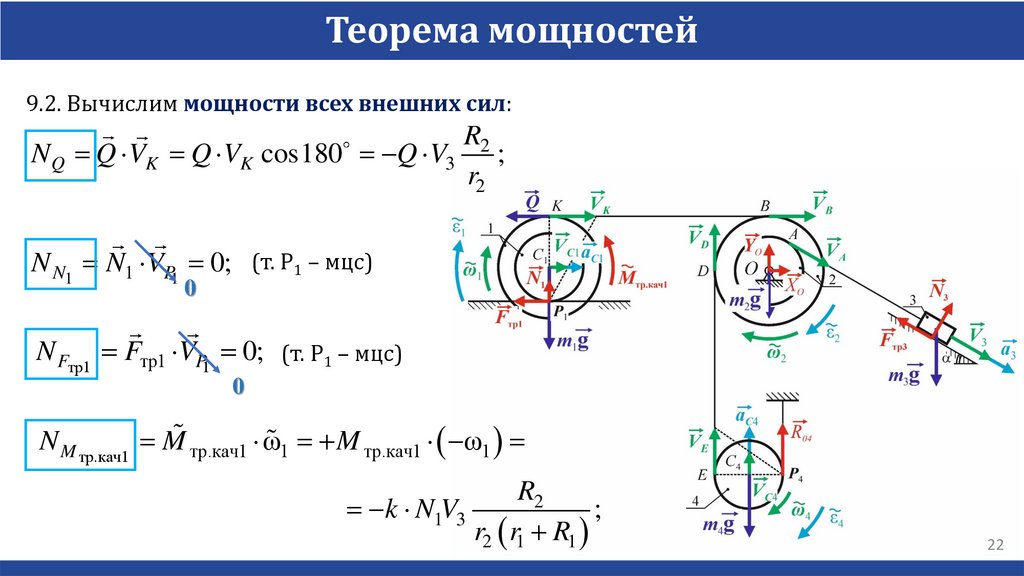
Теорема мощностей
9.2. Вычислим мощности всех внешних сил:
R2
NQ Q VK Q VK cos180 Q V3 ;
r2
N N1 N1 VP1 0; (т. P1 – мцс)
0
N Fтр1 Fтр1 VP1 0; (т. P1 – мцс)
0
N M тр.кач1 M тр.кач1 ω1 M тр.кач1 ω1
R2
k N1V3
;
r2 r1 R1
22

23.

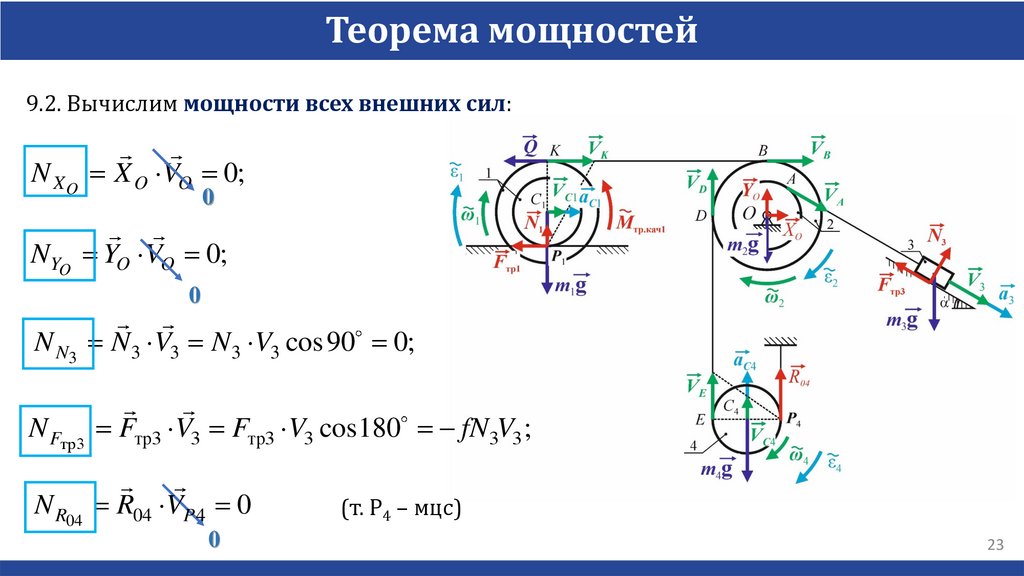
Теорема мощностей
9.2. Вычислим мощности всех внешних сил:
N X O X O VO 0;
0
NYO YO VO 0;
0
N N3 N3 V3 N3 V3 cos 90 0;
N Fтр3 Fтр3 V3 Fтр3 V3 cos180 fN 3V3 ;
N R04 R04 VP 4 0
0
(т. P4 – мцс)
23

24.

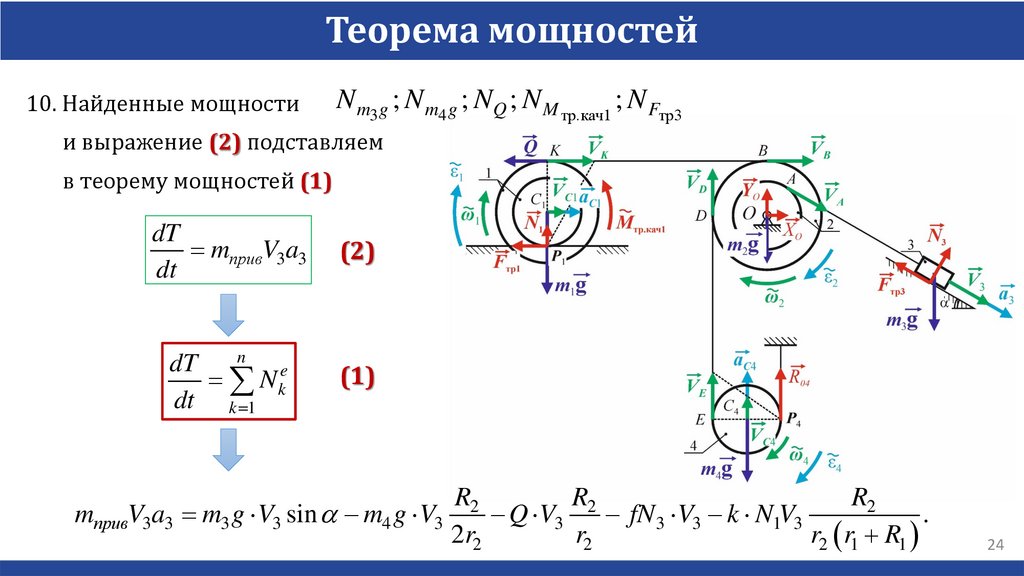
Теорема мощностей
10. Найденные мощности
N m3 g ; N m4 g ; NQ ; N M тр.кач1 ; N Fтр3
и выражение (2) подставляем
в теорему мощностей (1)
dT
mпривV3a3
dt
n
dT
N ke
dt k 1
(2)
(1)
R2
R2
R2
mпривV3a3 m3 g V3 sin a m4 g V3
Q V3
fN 3 V3 k N1V3
.
2r2
r2
r2 r1 R1
24

25.

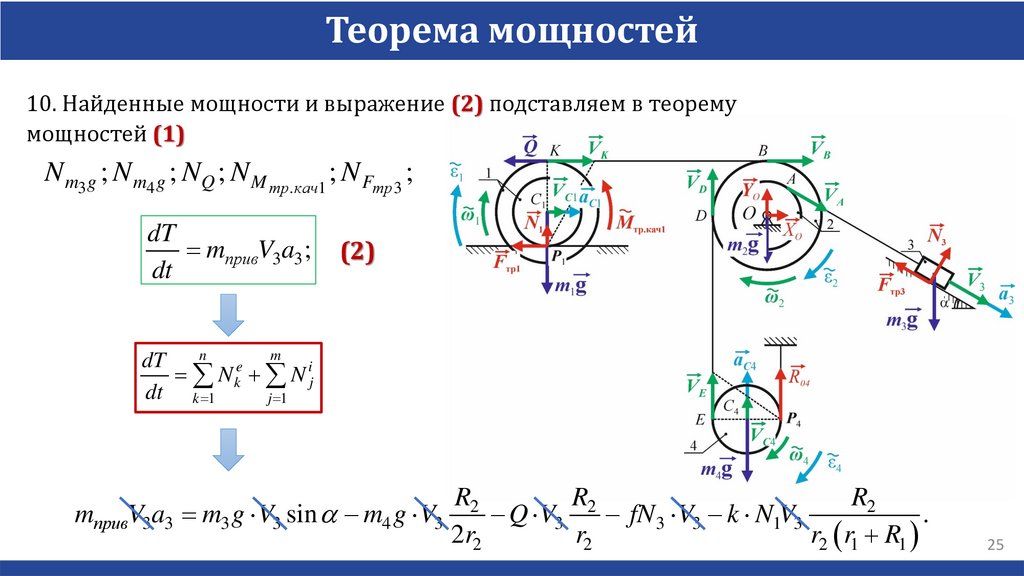
Теорема мощностей
10. Найденные мощности и выражение (2) подставляем в теорему
мощностей (1)
N m3 g ; N m4 g ; NQ ; N M тр.кач1 ; N Fтр 3 ;
dT
mпривV3a3 ;
dt
(2)
n
m
dT
e
N k N ij
dt k 1
j 1
R2
R2
R2
mпривV3a3 m3 g V3 sin a m4 g V3
Q V3
fN 3 V3 k N1V3
.
2r2
r2
r2 r1 R1
25

26.

Теорема мощностей
R2
R2
R2
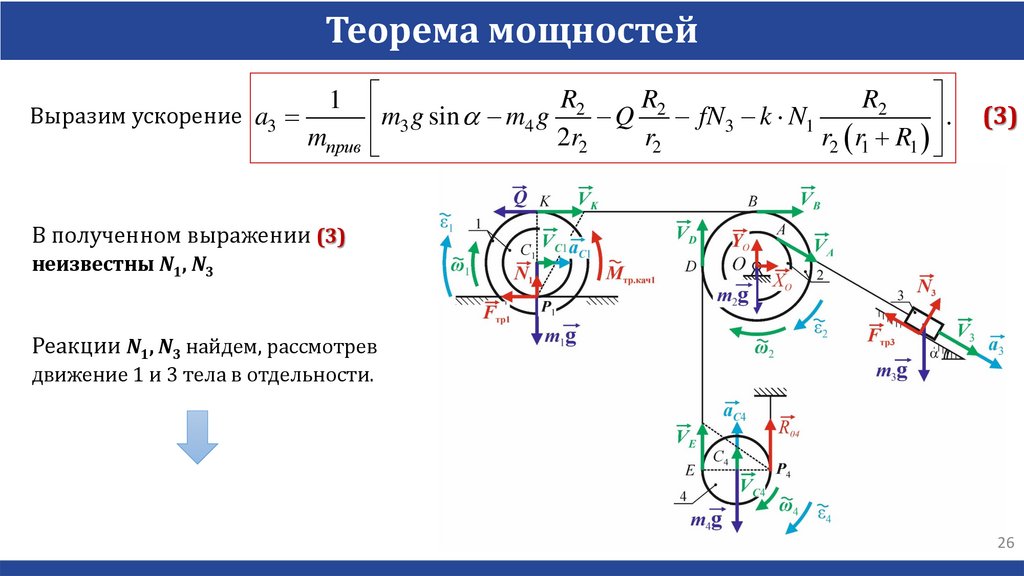
Выразим ускорение a3
Q
fN 3 k N1
m3 g sin a m4 g
.
mприв
2r2
r2
r2 r1 R1
1
(3)
В полученном выражении (3)
неизвестны N1, N3
Реакции N1, N3 найдем, рассмотрев
движение 1 и 3 тела в отдельности.
26

27.

Теорема мощностей
10. Рассмотрим плоскопараллельное движение тела 1 – колеса
10.1. Активные силы:
m1 g ; Q
10.2. Связи:
(0-1) – шероховатая поверхность;
(1-2) – гибкая невесомая нерастяжимая нить;
10.3. Заменим связи реакциями:
N1; Fтр1; M тр.кач1; R21
10.4. Система сил:
m g; Q; N ; F ; M
1
1
тр1
тр.кач1 ; R21
27

28.

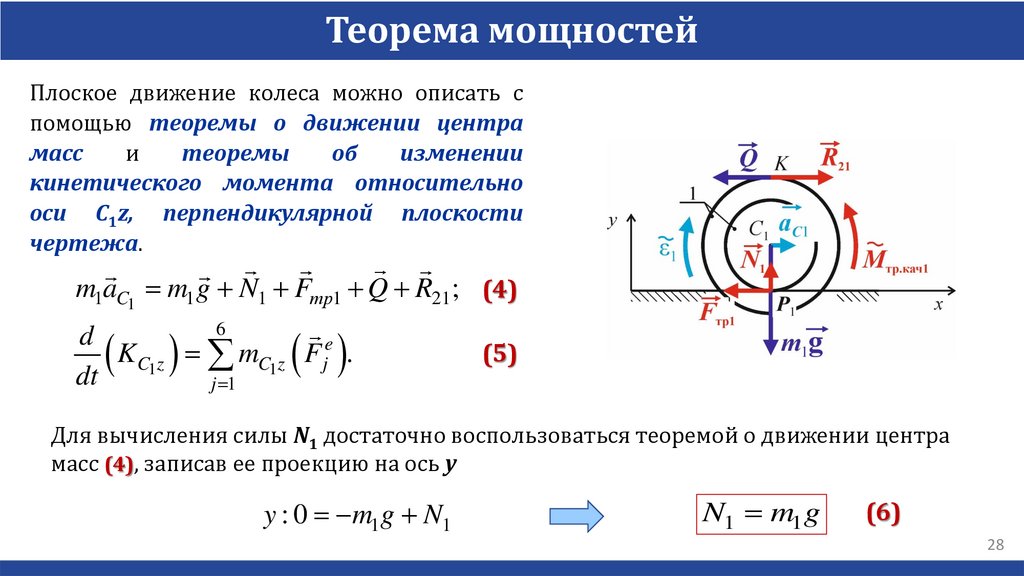
Теорема мощностей
Плоское движение колеса можно описать с
помощью теоремы о движении центра
масс
и
теоремы
об
изменении
кинетического момента относительно
оси C1z, перпендикулярной плоскости
чертежа.
m1aC1 m1 g N1 Fтр1 Q R21; (4)
6
d
KC1z mC1z F je .
dt
j 1
(5)
Для вычисления силы N1 достаточно воспользоваться теоремой о движении центра
масс (4), записав ее проекцию на ось y
y : 0 m1 g N1
N1 m1 g
(6)
28

29.

Теорема мощностей
11. Рассмотрим поступательное движение тела 3 – груза
11.1. Активные силы:
m3 g
11.2. Связи:
(0-3) – шероховатая поверхность;
(2-3) – гибкая невесомая нерастяжимая нить
11.3. Заменим связи реакциями:
N3 ; Fтр3 ; R23
11.4. Система сил:
m3 g; N3 ; Fтр3 ; R23
29

30.

Теорема мощностей
Движение груза 3 опишем с помощью
теоремы о движении центра масс
m3aC3 m3 g N3 Fтр 3 R23
(7)
В теорему (7) входит не только сила N3, но и реакция
нити R23, которую нужно определить по условию задачи.
Спроецируем выражение (7) на оси x и y
x : m3a3 m3 g sin a Fтр 3 R23
(8)
y : 0 m3 g cos a N 3
(9)
Fтр3 Fпред. f N3
(10)
тр3
N3 m3 g cos a
(11)
R23 m3 g sina fcosa a3
(12)
30

31.

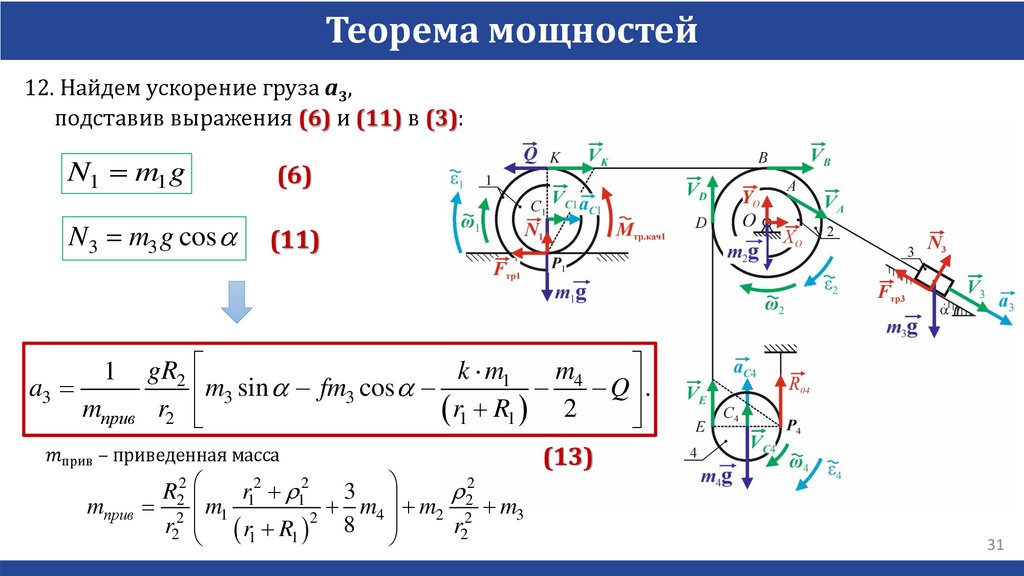
Теорема мощностей
12. Найдем ускорение груза a3,
подставив выражения (6) и (11) в (3):
N1 m1 g
(6)
N3 m3 g cos a
(11)
gR2
k m1
m4
a3
Q .
m3 sin a fm3 cos a
mприв r2
r1 R1 2
1