Dyn. Lek_6

1.

Новосибирский Государственный Архитектурно-Строительный
Университет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
ЛЕКЦИЯ 6.
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Кафедра теоретической механики

2.

План лекции
Введение
1 Кинетическая энергия механической
системы
2 Работа силы
3 Теорема об изменении кинетической энергии
4 Закон сохранения механической энергии
5 Решение задач с помощью теоремы
Заключение

3.

На предыдущих лекциях
Мы уже рассмотрели:
1. Теорему о движении центра масс системы
2. Теорему об изменении количества движения
(импульса) системы
3. Теорему об изменении момента количества
движения (момента импульса) системы
Дали рекомендации к решению задач на
применение этих теорем и рассмотрели примеры
решения этих задач

4.

Цель лекции
Изучить теорему об изменении
кинетической энергии

5.

НАПОМНИМ: МЕРЫ ДВИЖЕНИЯ
Введение
1 – центр масс системы
rC ( mk rk ) / M
2 – количество движения (импульс) системы
Q mk v k
3 – момент количества движения
(момент импульса) системы
KO M O (mk v k )
4 – кинетическая энергия системы
1
2
T ( mk v k )
2

6.

Введение
Напомним:
Движение механической системы мы будем
изучать по поведению ее характеристик (мер
движения) - центра масс, количества
движения, момента количества движения,
кинетической энергии
Поведение же этих характеристик будет
определяться теоремами об их изменении со
временем.
На этой лекции мы изучим четвертую теорему:
Теорему об изменении кинетической энергии

7.

Кинетическая энергия системы
В качестве четвертой меры движения
механической системы введем величину,
равную сумме кинетических энергий всех ее
точек и называемую кинетической энергией
механической системы
T mk v / 2
2
k
(1)
k
Кинетическая энергия (“живая сила”)
- характеристика поступательного и вращательного
движения системы
- величина скалярная (в отличии от Q и K 0 )
- определяется модулями скоростей ее точек
и не зависит от направления их движения

8.

Кинетическая энергия твердого тела
1. Поступательное движение
все точки тела движутся с одинаковыми скоростями
vk v
T mk v / 2 ( mk ) v / 2 Mv / 2
2
k
2
k
2
k
2. Вращательное движение вокруг оси Z
v k hk
- скорости точек
T mk v 2k / 2 ( mk hk2 ) 2 / 2 J z 2 / 2
k
k
J z - момент инерции тела относительно оси Z

9.

3. Произвольное движение твердого тела
- можно рассматривать как сумму поступательного движения
вместе с центром масс С и вращательного движения вокруг
мгновенной оси вращения, проходящей через С
согласно теореме о сложении скоростей
v k v kr v ke
v kr
v ke v C
относительная скорость вращательного
движения вокруг мгновенной оси вращения
C
переносная скорость поступательного
движения вместе с его центром масс С
v v k v k ( v kr v C ) ( v kr v C ) v v 2 v kr v C
2
k
2
kr
2
C

10.

v kr hk
hk - расстояние от точки до оси вращения
C
Получим
T mk v 2k / 2 ( mk ) v C2 / 2 ( mk hk2 ) 2 / 2 ( mk v kr ) v C
k
k
k
k
Заметим, что
m v Mv
k
kr
Cr
k
v Cr - относительная скорость вращения
центра масс вокруг оси
C

11.

Так как ось
C проходит через точку С, то v Cr 0
и мы получим Теорему Кенига
T Mv / 2 J C / 2
2
C
2
(2)
Теорема Кенига:
кинетическая энергия тела при его произвольном
движении складывается из кинетической энергии его
поступательного движения вместе с центром масс и
кинетической энергии его вращательного движения
вокруг оси, проходящей через центр масс
В частности:
Кинетическая энергия плоского движения
твердого тела
T Mv / 2 J C / 2
2
C
2
(3)

12.

Забегая вперед, приведем ответ:
Теорема об изменении кинетической энергии
в интегральной форме
T2 T1 A A
e
12
i
12
изменение кинетической энергии системы
равно сумме работ всех действующих на
нее внешних и внутренних сил
Перейдем теперь к определению
работы силы

13.

Работа силы
Вспомним школу: точка М движется
прямолинейно и F const
F
α
M
M1
S
(5)
t t 2 t1
M2
A12 F s
s M1M 2
- скалярное произведение
A12 Fs cos
F - вектор силы
s - вектор перемещения точки
- угол между вектором силы и перемещением точки

14.

Работа силы (общий случай)
M2
vα
Разобьем отрезок кривой на
малые отрезки
A12 Fk s k cos k F s k
k
k
M
F
M1
A12
Точное значение работы получим,
переходя к пределу
F(s) ds F (s) cos (s)ds F (s)ds
M 1M 2
M 1M 2
M 1M 2
F - проекция силы на направление
перемещения точки
(6)

15.

Элементарная работа
A F(s) ds F (s) cos (s)ds F (s)ds
Единицей измерения работы - 1 джоуль (1нм).
Если сила задана как функция положения точки
F F ( x, y , z )
x2
y2
z2
x1
y1
z1
A12 Fx dx Fy dy Fz dz
При естественном способе задания движения точки
s2
s2
s1
s1
A12 F ( s) cos ( s)ds F ( s)ds

16.

Если сила известна как функция времени
t2
ds vdt
A12 F(t ) v(t )dt
t1
Мощность силы – [Ватт = Джоуль/сек]
ds dA
N (t ) F(t ) v (t ) F ( s ) v(s) F ( s )
dt dt
t2
A12 N (t )dt
t1
Если
N (t ) N const A12 N (t 2 t1 )
Техническая единица измерения работы- киловатт-час

17.

Работа силы тяжести
g (0,0, g )
Ak mk gdz k
проекции вектора,
ось Z направлена вверх
- элементарная работа
A Ak g mk dz k gd ( mk z k ) gd ( Mz C ) gMdz C
k
k
k
zC 2
A12 Mg dz C Mg ( z C 2 z C1 ) MghC (7)
zC 1
Работа силы тяжести механической системы равна ее весу
умноженному на вертикальное перемещение ее центра
тяжести
hC 0 A 0 - центр тяжести опускается
hC 0 A 0 - центр тяжести поднимается

18.

Работа силы упругости
F c
l1 ,l2
- начальная и конечная длина пружины
1 l1 l0
l2
l l0
2 l2 l0
l2
A12 c cos 180 dl c(l l0 )dl c( 12 22 ) / 2
l1
(8)
l1
Работа силы упругости равна половине произведения
коэффициента жесткости на разность квадратов
начального и конечного удлинений пружины.

19.

Работа силы трения скольжения
M2
N
Ff
ds
M
M1
F f ds F f ds
- сила трения направлена
против движения
s2
s2
s1
s1
A12 F f ds f N ( s)ds
При движении тела по горизонтальной поверхности
N mg const
A12 fN (s2 s1 )
(9)

20.

Работа сил,
приложенных к твердому телу
1. Работа всех внутренних сил равна нулю
ds1 α
1
M1
F1
M2
α2
F2
ds 2
F1 F2 ; ds1 cos 1 ds2 cos 2
A1 A2 F1ds1 cos 1 F2 ds2 cos 2 0

21.

2. Работа внешних сил:
- при поступательном движении
e
e e
A A Fk d sk ( Fk )d s R d s
e
e
k
k
k
k
- при вращательном
движении
vk
Mk
rk
ω
O
e
e
e
e
e
A Ak Fk d sk Fk v k dt Fk ( r )dt
k
k
k
k
e
e
(rk Fk ) dt M o dt M ze dt M ze d
k
e
Таким образом : A M d , M M z ( Fk )
e
e
z
e
z
k

22.

- при произвольном движении
Ω
e
M - главный момент внешних сил
R - главный вектор внешних сил
e
M
dr0 - вектор перемещения полюса О
O
Re
e
- мгновенная ось вращения
dr0
A R dr0 M d
e
e
e
Элементарная работа внешних сил, приложенных к
твердому телу равна сумме элементарных работ главного
вектора на перемещении точки его приложения – полюса, и
главного момента этих сил относительно мгновенной оси
вращения, проходящей через этот полюс, на приращении
угла поворота

23.

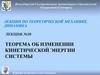
Работа сил трения, действующих
на катящееся колесо
N
vС
C
MK
N
Ff M K
AN Aтр 0
Ak M k d
Ff
P
P - МЦС
M k Nk
k - коэффициент трения качения
d dsC / R
Ak kNdsC / R

24.

Теорема об изменении
кинетической энергии
второй закон Ньютона для системы
dv k
mk
Fke Fki
dt
Умножим скалярно на v k обе части уравнения
dv k
mk v k
Fke v k Fki v k
dt
mk v k dv k Fke ds k Fki ds k
Просуммируем теперь все уравнения
с учетом соотношений
mk v k dv k d (mk v 2k / 2)

25.

получим
2
e
i
d
(
m
v
/
2
)
A
A
k k
k k
k
k
(14)
k
Теорема об изменении кинетической энергии
в дифференциальной форме
dT A A
e
i
(15)
в интегральной форме
T2 T1 A A
e
12
i
12
(16)
изменение кинетической энергии системы
равно сумме работ всех действующих на
нее внешних и внутренних сил

26.

Отличие теоремы об изменении
кинетической энергии от других теорем
T2 T1 A A
e
12
i
12
(16)
1. Уравнение (16) скалярное, и, следовательно,
позволяет получить лишь одно уравнение
движения механической системы
2. В теорему входят как внешние, так и внутренние
силы, действующие на механическую систему.
То есть под действием внутренних сил
кинетическая энергия может изменяться

27.

Примеры:
• Движение автомобиля. Движущаяся сила – сила трения
между колесами и дорогой работу не производит!
Производят работу – внутренние силы давления газов и
силы трения в движущихся частях автомобиля.
• Выстрел снаряда. Работу совершают силы давления
пороховых газов. Они то и придают скорость снаряду.
• Движение колеса без проскальзывания. Работу
производит момент сопротивления качению. Т.к. он мал,
то колесо может катиться очень долго.
• Примеры сил, работа которых равна нулю:
- внутренние силы твердого тела
- реакции идеальных связей (гладкой опоры, шарниров с
идеальной смазкой
- сил, приложенных к неподвижным или мгновенно
неподвижным точкам

28.

Потенциальная (консервативная) сила
2
1
1,2,3 - траектории
M2
3
A12
M1
F(s) ds
M 1M 2
Сила называется потенциальной (или консервативной),
если работа этой силы на любом перемещении не зависит
от формы траектории, по которой оно совершается
Потенциальная энергия силы F – это ее работа при
перемещении из положения М(x,y,z) в положение O(0,0,0)
П ( x, y, z ) F( s)ds
MO
A12 П1 П2
(17)

29.

A12 П1 П2
(17)
П1 , П2 - потенциальная энергия в точках 1 и 2,
зависит только от положения в пространстве
Таким образом, все силы, действующие на
механическую систему можно разделить на
потенциальные и непотенциальные
Если все действующие на механическую
систему силы потенциальны
(консервативны), то она называется
консервативной

30.

Закон сохранения механической энергии
T2 T1 A12 ( П1k П 2 k ) П1 П 2
k
k
T2 П2 T1 П1
(18)
Закон сохранения механической энергии:
для консервативных систем
полная механическая энергия T+П сохраняется
Если система неконсервативна, то есть среди сил,
действующих на нее, есть непотенциальные силы,
то полная механическая энергия не сохраняется.

31.

Решение задач с помощью теоремы
Уточним рекомендации к решению задач:
1
2
3
Выбрать механическую систему (удачно!)
Изобразить все нужные силы (внешние и внутренние,
производящие работу)
Записать теорему об изменении кинетической
энергии
Замечания:
1. Теорема обычно применяется для систем,
отдельные части которых совершают разные
типы движений – поступательное, вращательное,
плоское
2. Теорема дает лишь одно уравнение, поэтому задачу
нужно сводить к одной неизвестной, используя
кинематические связи
3. Часто теорема используется вместе с другими
теоремами динамики.

32.

Задача 1
m1g
Ff
N
y0
2
x0
m2g
3
Дано: m1,m2,m3,r1,r2,J2
Каток - однородный диск,
катится без проскальзывания.
Груз 3 – опускается на высоту h
Определить: v3(h)
Решение.
1. М.С. – вся конструкция.
2. Работа сил.
Ae Ai m3g s3 A mgh
P
m3g
3. Кинетическая энергия.
T T1 T2 T3 ; T1 m1VC21 / 2 J C1 12 / 2; T2 J 2 22 / 2; T3 m3V32 / 2
2 V3 / r2 ; 1 V3 / 2r1; VC1 1r1; J C1 m1r12 / 2
T (3m1 / 16 J 2 / 2r22 m3 / 2)V32
Применим теорему.
T (h) T (o) mgh; T (0) 0 V3 2m3 gh /(3m1 / 8 J 2 / r22 m3 )
Противоречие с опытом: V3>0 при любом малом m3.
Причина – не учли трение качения.

33.

Задача 2
h
mg
Дано: m, h, c
Определить: наибольшее сжатие
пружины d
c
Решение.
1. М.С.- груз
e
i
2
2. Работа сил. A A A mg (h d ) cd
2
2
mV2 / 2 mV0 / 2 A;
3. Применим теорему.
V0 0; V2 0 A 0 d mg (mg / c) 2 2mgh / c
Замечания:
1. Задачу можно решить и с помощью второго закона
Ньютона, разбив движение на два участка:
до соприкосновения груза с пружиной и после.
Но было бы сложнее!
2. По-существу, при решении мы применили закон
сохранения энергии

34.

Задача 3
R2
Дано: JAB=J, m
Ve
ω0
A
M
Vr
R1
mg
B
AM x; (0) 0 , Vr (0) 0, x(0) 0
Определить: Vr (x)
Решение.
1. М.С. – вся конструкция (трубка + шарик)
A A e Ai 0
3. Кинетическая энергия.
T J 2 / 2 mV 2 / 2;
V Vr Ve V 2 Vr2 Ve2 Vr2 2 x 2 ; T J 2 / 2 m(Vr2 2 x 2 ) / 2
Применим теорему. T (t ) T (0) Vr J ( 02 2 ) / 2 x 2 2
Для определения применим теорему моментов:
e
2
M
(
F
)
0
K
const
K
(
0
)
J
mx
J 0
z k
z
z
Следовательно,
Vr ( x) 0 x J /( J mx2 )
Замечание. Для решения мы применили две теоремы!

35.

Задача 4
m, J A J , (0) 0 ,
Дано:
V (0) 0, z (0) z0
A
Трением пренебречь
φ0
C0
z0
Определить :
C
z
(z )
Решение.
1. М.С. – маятник.
Система консервативна. Применим закон сохранения
полной механической энергии
T П П 0 J / 2 mgz mgz0
2
Следовательно,
( z ) 2mg ( z0 z ) / J

36.

Заключение
1. Определена кинетическая энергии
системы и выведены формулы ее расчета
для частных случаев движения твердого
тела
2. Определено понятие работы силы и
выведены формулы ее расчета.
3. Изучена теорема об изменении
кинетической энергии и ее частный
случай - закон сохранения энергии
4. Рассмотрены решения задач с
использованием теоремы

37.

Вопросы для самоконтроля
1. Как определяется и что характеризует кинетическая энергия
механической системы?
2. Как вычисляется кинетическая энергия для твердого тела в
случаях его поступательного и вращательного движений?
3. В чем состоит теорема Кенига?
4. Как определяется работа постоянной силы на
прямолинейном перемещении точки, к которой она
приложена? А если сила переменная и точка перемещается
по кривой?
5. Что понимают под элементарной работой силы и как она
связана с работой силы на конечном перемещении точки, к
которой она приложена? В каких случаях элементарная
работа равна нулю?
6. Приведите формулы для вычисления работы силы в
случаях, когда она задана как функция времени, естественной
координаты движения точки, прямоугольных декартовых
координат точки, скорости точки.

38.

Вопросы для самоконтроля
7. Что называется мощностью силы? В каких единицах она
измеряется?
8. Чему равна работа силы тяжести ? А работа силы
упругости и сил трения?
9. Почему работа всех внутренних сил твердого тела равна
нулю? Для каких еще тел работа внутренних сил равна нулю?
10. Чему равна работа внешних сил, приложенных к твердому
телу при его поступательном, вращательном и плоском
движении? А если движение твердого тела произвольное?
11. Дайте формулировку теоремы об изменении кинетической
энергии в дифференциальной и интегральной форме. Чем
эта теорема отличается от остальных общих теорем
динамики?
12. Приведите примеры механических систем, для которых
работа внутренних сил не равна нулю. А в каких случаях она
равна нулю?

39.

Вопросы для самоконтроля
13. Дайте рекомендации к решению задач на применение
теоремы об изменении кинетической энергии. В каких случаях
движения механических систем эту теорему удобнее всего
применять? Сколько уравнений можно получить с ее
помощью?
14. Как определяется потенциальная энергия? Для любой ли
силы можно ее определить? Для каких из сил существует
потенциальная энергия: тяжести, сопротивления среды
(воздуха, воды), упругости пружины, всемирного тяготения,
трения скольжения, трения качения?
15. В чем состоит закон сохранения полной механической
энергии? Для каких механических систем она сохраняется?
Приведите примеры, когда полная механическая энергия
системы сохраняется; возрастает; убывает со временем.