4c0357a235214530900461dc19d697cf

1.

Колебательное движение

2.

Колебательное движение
Колебательное движение – это такое
движение тела, при котором значения кинематических
характеристик (координата, скорость, ускорение) периодически повторяются с течением времени.
Вращательное движение – одно из такого типа движения.

3.

Условия колебательного движения
Колебательная система - такая система, в
которой в результате отклонения возникает
сила, возвращающая систему в положение
устойчивого равновесия, и система переходит
в колебательное движение.
Свободные колебания - колебания, которые происходят только за счет запасенной начальной энергии.

4.

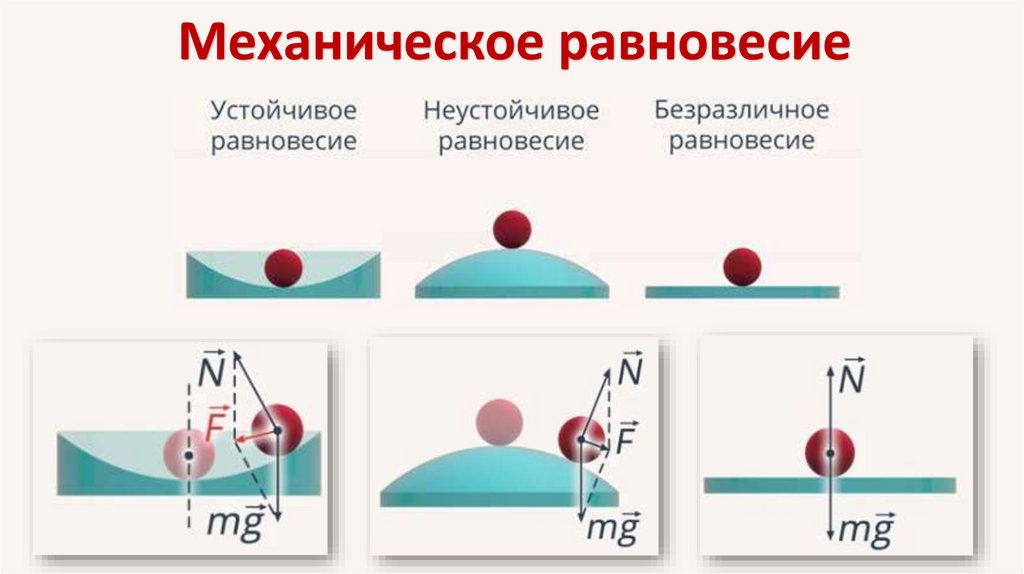
Механическое равновесие

5.

Точка устойчивого равновесия.
Именно вокруг этой точки и совершаются
колебания.

6.

Свободные колебания
Свободными называют колебания, которые
происходят только под действием внутренних сил
системы.

7.

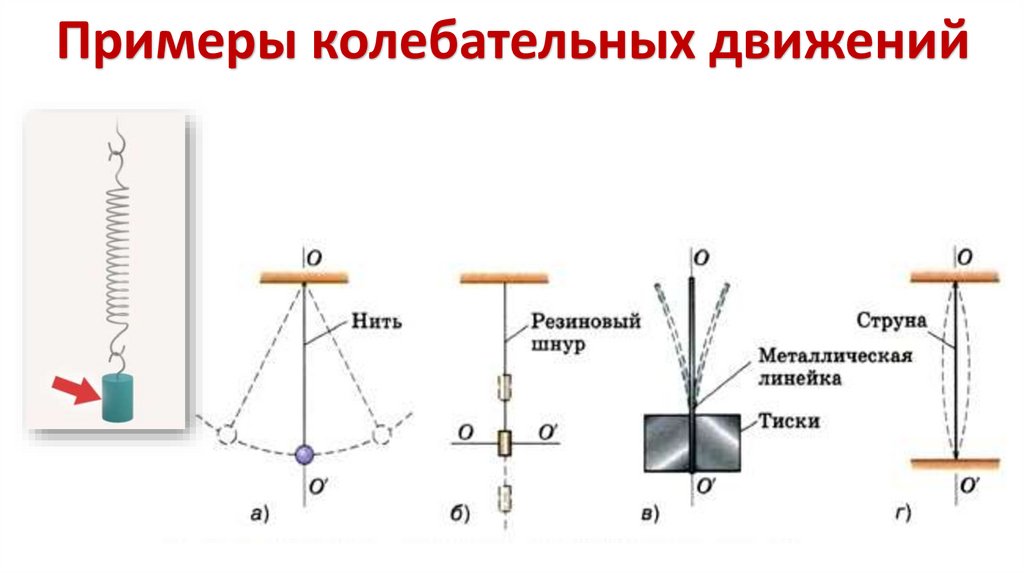
Примеры колебательных движений

8.

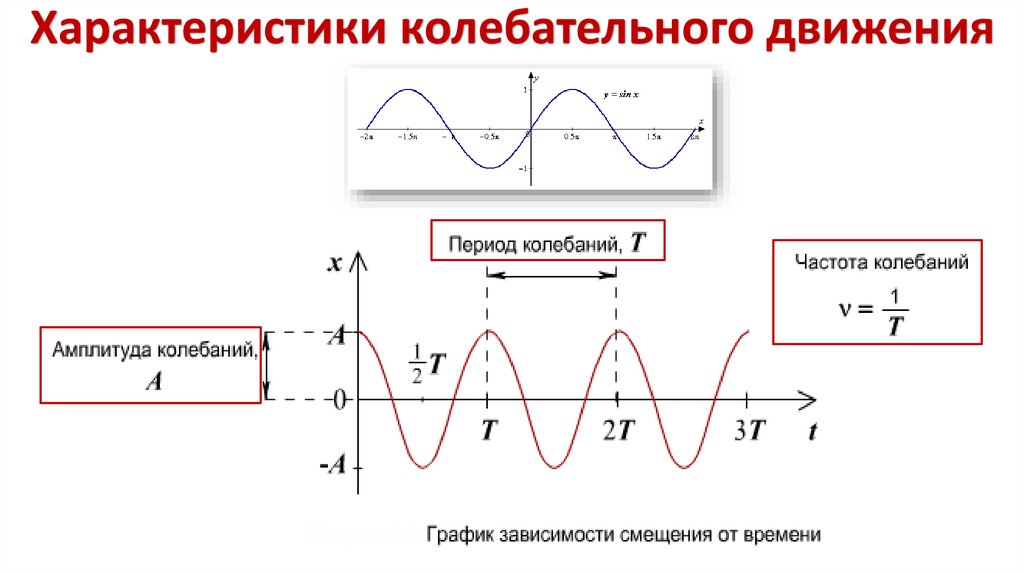
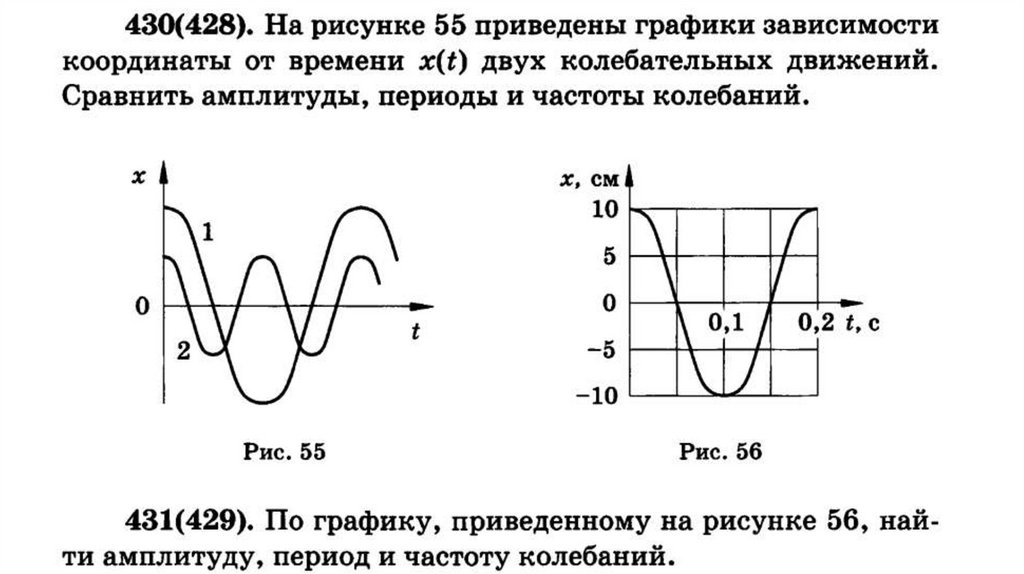
Характеристики колебательного движения
Амплитуда колебаний – максимальное отклонение (по
модулю) координаты тела от положения его равновесия.
А, Xm [м]
Амплитуда скорости – максимально значение скорости колеблющегося тела.
Амплитуда ускорения – максимальное значение ускорения колеблющегося тела.
Период колебаний – промежуток времени, по прошествии
которого значение координаты, скорости, ускорения и возвращающей силы повторяются.
Частота колебаний – число полных колебаний, совершаемых в единицу времени.
T [сек]
ν [Гц]

9.

Характеристики колебательного движения

10.

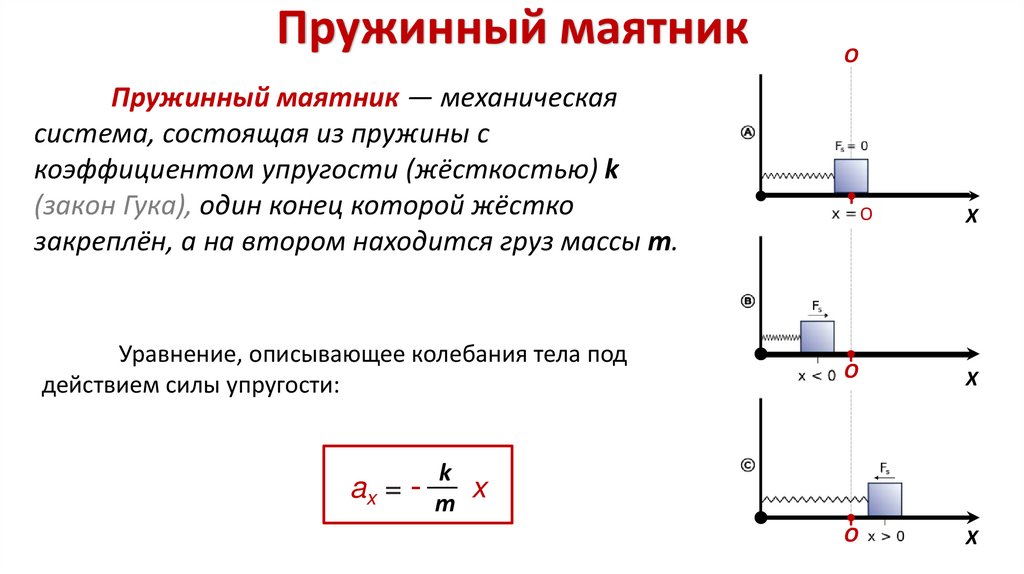
Пружинный маятник
O
Пружинный маятник — механическая
система, состоящая из пружины с
коэффициентом упругости (жёсткостью) k
(закон Гука), один конец которой жёстко
закреплён, а на втором находится груз массы m.
Уравнение, описывающее колебания тела под
действием силы упругости:
O
X
O
X
O
X
k
ax = - m x

11.

Пружинный маятник
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости
(жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
Период колебаний пружинного маятника может быть
вычислен по следующей формуле:

12.

Математи́ческий мая́ тник
Математи́ческий ма́ятник представляет собой механическую
систему, состоящую из материальной точки на конце невесомой
нерастяжимой нити или лёгкого стержня и находящуюся в однородном
поле сил тяготения. Другой конец нити (стержня) неподвижен.
g
Уравнение, описывающее колебания
математи́ческого ма́ ятника:
a=-
g
l
l
x
X0
X1
O
X

13.

Математи́ческий мая́ тник
Математи́ческий ма́ятник представляет собой механическую систему, состоящую из
материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся
в однородном поле сил тяготения. Другой конец нити (стержня) неподвижен.
Период собственных колебаний математического
маятника длины l, подвешенного в поле тяжести,
равен:
l

14.

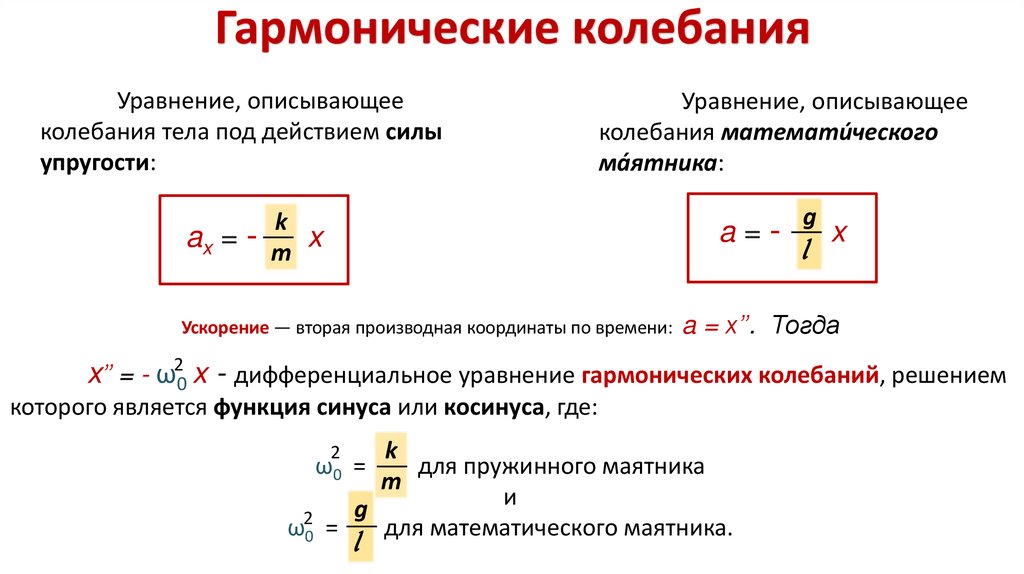
Гармонические колебания
Уравнение, описывающее
колебания тела под действием силы
упругости:
k
ax = - m x
Уравнение, описывающее
колебания математи́ческого
ма́ятника:
a=-
Ускорение — вторая производная координаты по времени: a = x’’.
g
l
x
Тогда
x’’ = - ω20 x - дифференциальное уравнение гармонических колебаний, решением
которого является функция синуса или косинуса, где:
k
ω0 =
для пружинного маятника
m
и
g
ω20 =
для математического маятника.
2
l

15.

Гармонические колебания
Гармонические колебания — это колебания, при которых координата зависит от
времени по гармоническому закону (по закону синуса или косинуса):
x = A cos(ωt + α)
или
x = A sin(ωt + α).
Положительная величина A является наибольшим по модулю значением координаты (так
как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от
положения равновесия. Поэтому A — амплитуда колебаний (или Xm).
Аргумент косинуса ωt+α называется фазой колебаний. Величина α, равная значению фазы
при t = 0, называется начальной фазой. Начальная фаза отвечает начальной координате тела:
x0 = A cosα.
Величина ω называется циклической частотой. Найдём её связь с периодом колебаний T и частотой ν.
Одному полному колебанию отвечает приращение фазы, равное 2π радиан:
ωT = 2π, откуда:
ω = 2π / T или ω = 2π ν.
Иными словами циклическая частота ω это количество колебаний за 2π секунд.
Измеряется циклическая частота в рад/с (радиан в секунду).

16.

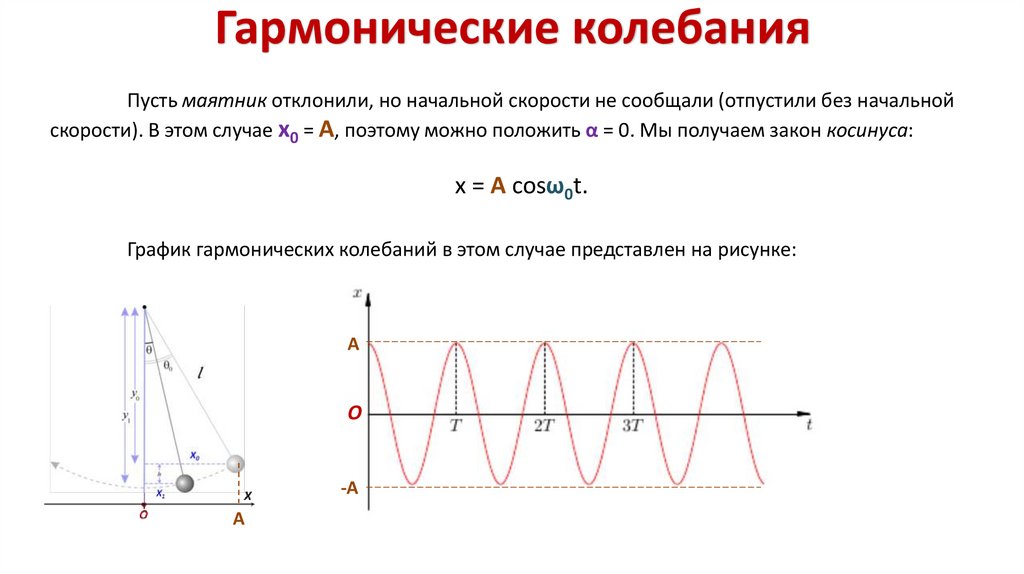
Гармонические колебания
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной
скорости). В этом случае x0 = A, поэтому можно положить α = 0. Мы получаем закон косинуса:
x = A cosω0t.
График гармонических колебаний в этом случае представлен на рисунке:
A
O
-A
A

17.

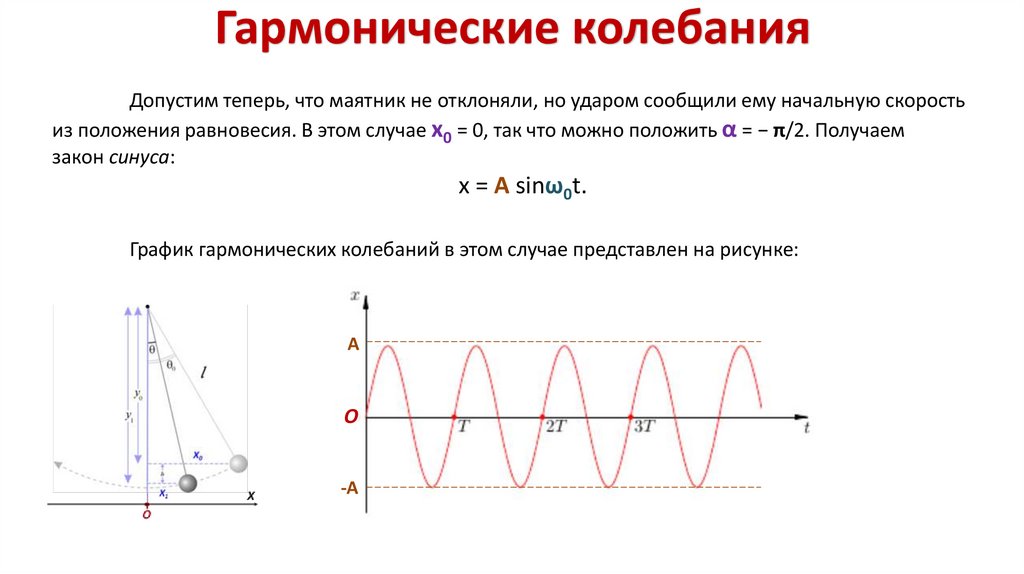
Гармонические колебания
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость
из положения равновесия. В этом случае x0 = 0, так что можно положить α = − π/2. Получаем
закон синуса:
x = A sinω0t.
График гармонических колебаний в этом случае представлен на рисунке:
A
O
-A

18.

Гармонические колебания
Уравнение скорости и ускорения
Пусть колебания описываются уравнением:
x = A cosω0t.
Найдём скорость точки, совершающей гармонические колебания:
V = x’ = (A cosω0t)’= - Aω0 sinω0t
Дифференцируем полученное равенство – это уравнение ускорения:
2
a = V ’ = x’’ = (- Aω0 sin ω0t)’= - Aω0 sinω0t
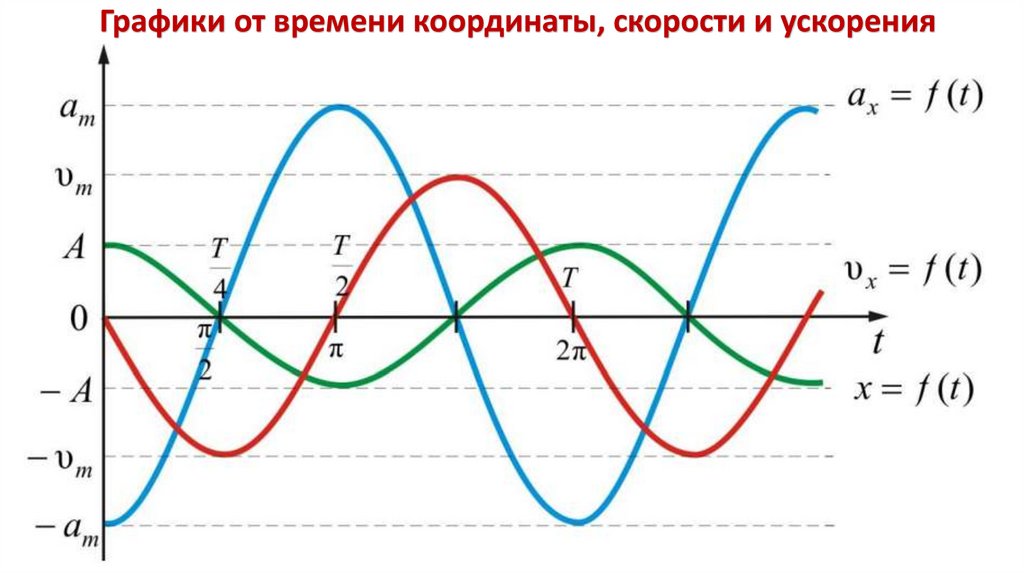
Графики от времени координаты, скорости и ускорения представлены на следующем слайде.

19.

Графики от времени координаты, скорости и ускорения

20.

Превращения энергии при свободных
механических колебаниях
Полная механическая энергия при гармонических колебаниях равна сумме
кинетической Wk и потенциальной Wp энергий колебательной системы.
Для пружинного маятника имеем:
W = Wk + Wp
2
2
2
mv ____
kx
kxm
____
____
=
+
=
= const
2
2
2
Для математического маятника:
2
mv
____
W = Wk + Wp =
+ mgh = const
2

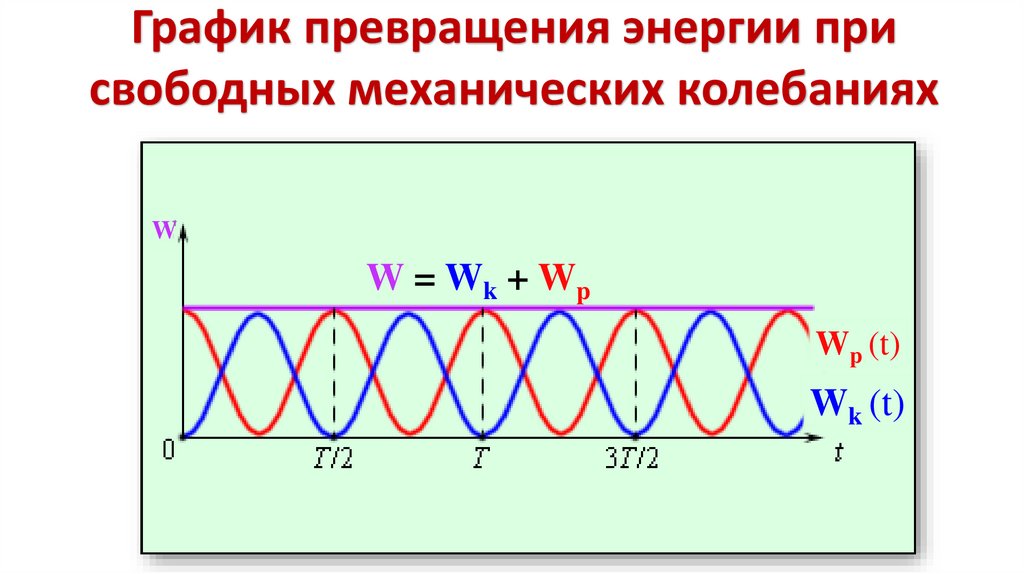
21.

График превращения энергии при
свободных механических колебаниях
W = Wk + Wp = ____ + ____ = ____ = const
W
W = Wk + Wp
Wp (t)
Wk (t)

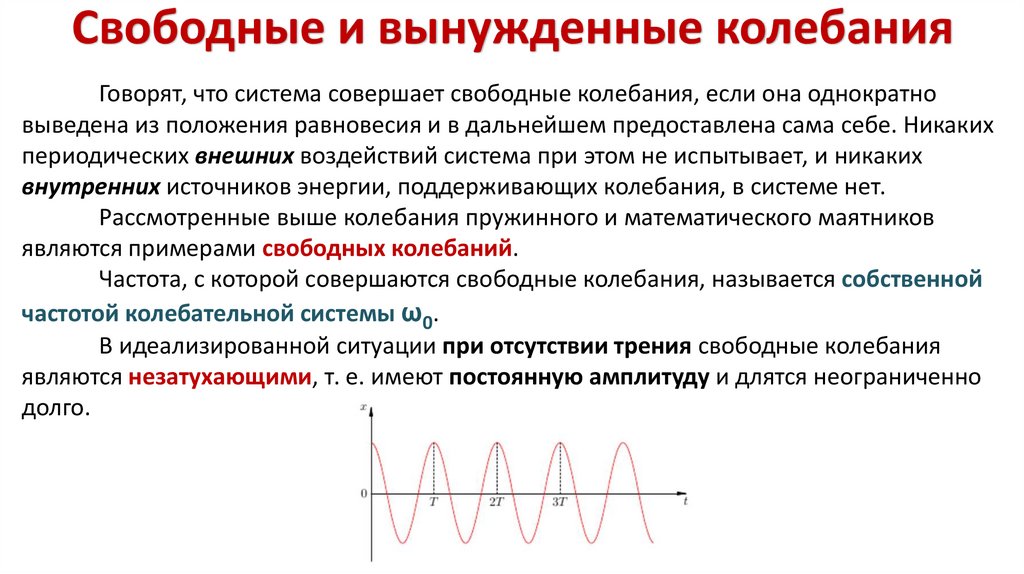
22.

Свободные и вынужденные колебания
Говорят, что система совершает свободные колебания, если она однократно
выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких
периодических внешних воздействий система при этом не испытывает, и никаких
внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников
являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной
частотой колебательной системы ω0.
В идеализированной ситуации при отсутствии трения свободные колебания
являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно
долго.

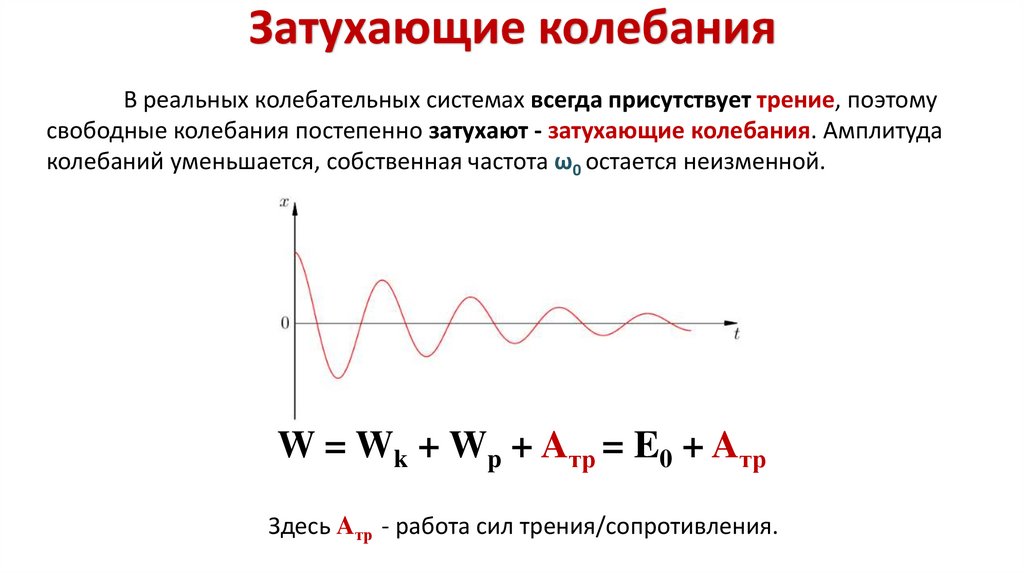
23.

Затухающие колебания
В реальных колебательных системах всегда присутствует трение, поэтому
свободные колебания постепенно затухают - затухающие колебания. Амплитуда
колебаний уменьшается, собственная частота ω0 остается неизменной.
W = Wk + Wp + Aтр = E0 + Aтр
Здесь Aтр - работа сил трения/сопротивления.

24.

Вынужденные колебания
Свободные колебания - колебания, которые происходят только за счет запасенной начальной энергии.
Колебания, совершающиеся под воздействием внешней
периодической силы, называются вынужденными.
Работа внешней силы Aвн над системой обеспечивает приток энергии к системе
извне, что не даёт колебаниям затухнуть, несмотря на действие сил трения.
W = Wk + Wp + Aтр + Aвн

25.

Вынужденные колебания
Колебания, совершающиеся под воздействием внешней периодической силы,
называются вынужденными.
Работа внешней силы Aвн над системой обеспечивает приток энергии к системе
извне, что не даёт колебаниям затухнуть, несмотря на действие сил трения.
W = Wk + Wp + Aтр + Aвн
Aтр + Aвн < 0 - энергия колебательной системы уменьшается - затухающие колебания.
Aтр + Aвн = 0 - энергия колебательной системы не изменяется установившиеся вынужденные колебания.
Aтр + Aвн > 0 - энергия колебательной системы увеличивается.

26.

Вынужденные колебания
Aтр + Aвн > 0 - энергия колебательной системы увеличивается.
Предположим, что собственная частота колебаний системы равна ω0, а вынуждающая сила
зависит от времени по гармоническому закону:
F (t) = F0 cosωt .
В течение некоторого времени происходит установление вынужденных колебаний: система
совершает сложное движение, которое является наложением вынужденных и свободных колебаний.
Свободные колебания постепенно затухают, и в установившемся режиме система совершает
вынужденные колебания, которые также оказываются гармоническими. Частота установившихся
вынужденных колебаний совпадает с частотой ω вынуждающей силы (внешняя сила как бы
навязывает системе свою частоту).
Свойства вынужденных колебаний:
- частота установившихся колебаний равна частоте ω вынуждающей силы;
- амплитуда установившихся колебаний Xm зависит от частоты ω (ν) вынуждающей силы.

27.

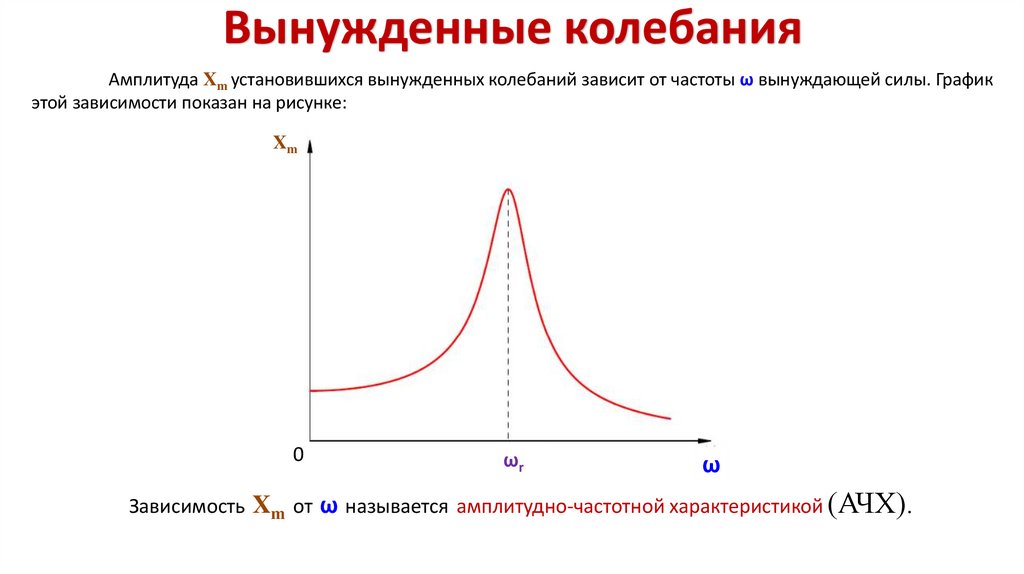
Вынужденные колебания
Амплитуда Xm установившихся вынужденных колебаний зависит от частоты ω вынуждающей силы. График
этой зависимости показан на рисунке:
Xm
0
ωr
ω
Зависимость Xm от ω называется амплитудно-частотной характеристикой (АЧХ).

28.

Вынужденные колебания. Резонанс
Xm
0
ωr
ω
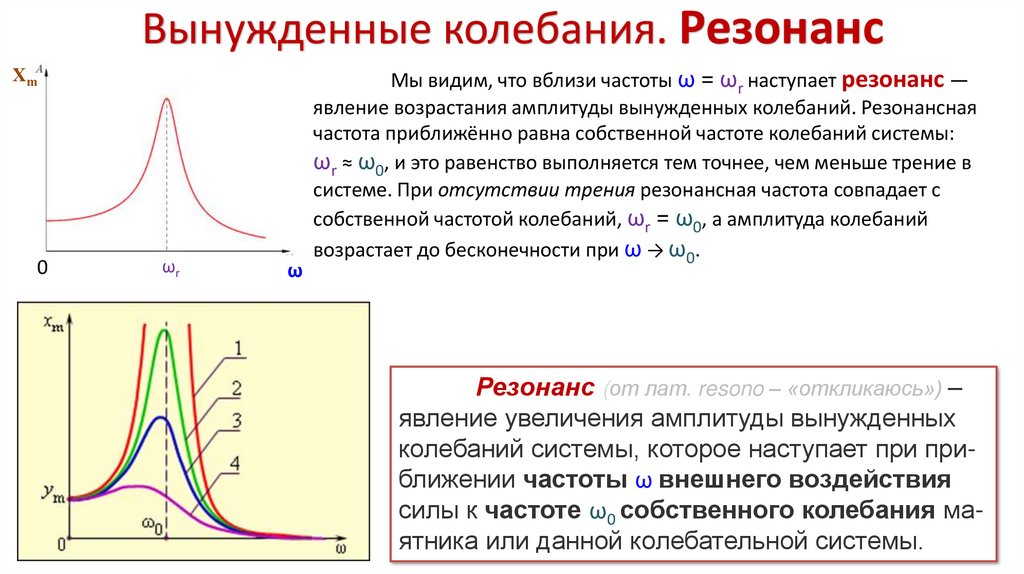
Мы видим, что вблизи частоты ω = ωr наступает резонанс —
явление возрастания амплитуды вынужденных колебаний. Резонансная
частота приближённо равна собственной частоте колебаний системы:
ωr ≈ ω0, и это равенство выполняется тем точнее, чем меньше трение в
системе. При отсутствии трения резонансная частота совпадает с
собственной частотой колебаний, ωr = ω0, а амплитуда колебаний
возрастает до бесконечности при ω → ω0.
Резонанс (от лат. resono – «откликаюсь») –
явление увеличения амплитуды вынужденных
колебаний системы, которое наступает при приближении частоты ω внешнего воздействия
силы к частоте ω0 собственного колебания маятника или данной колебательной системы.

29.

Вынужденные колебания. Автоколебания.
Существуют системы, в которых
незатухающие колебания возникают не за счет
периодического внешнего воздействия, а в
результате имеющейся у таких систем
способности самой регулировать поступление
энергии от постоянного источника. Такие
Ходовое колесо
системы называются автоколебательными,
а процесс незатухающих колебаний в таких
системах – автоколебаниями. В автоколеМаятник
бательной системе можно выделить три
характерных элемента – колебательная
система, источник энергии и устройство
обратной связи между колебательной
системой и источником.
Анкер
Гиря

30.

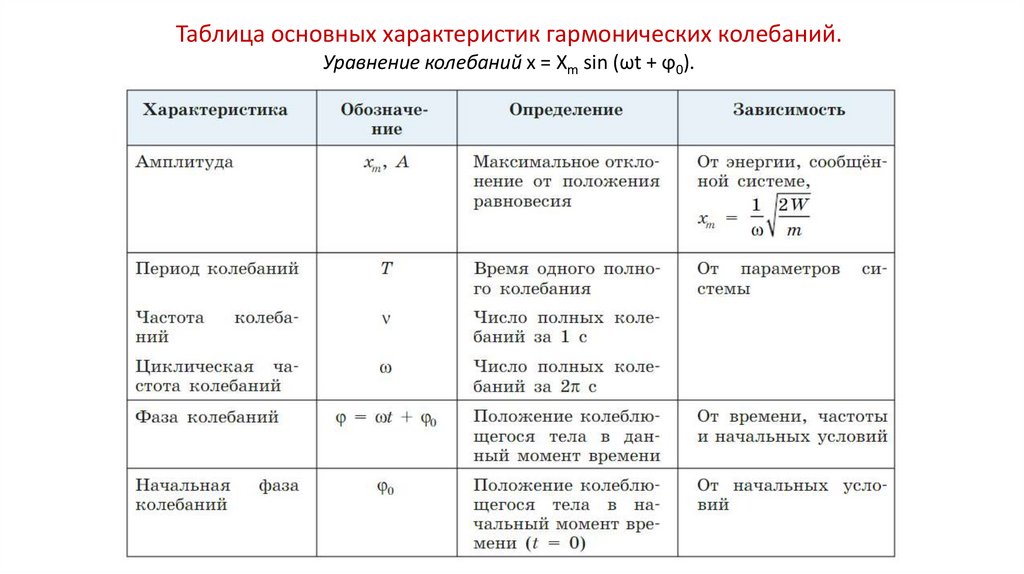
Таблица основных характеристик гармонических колебаний.
Уравнение колебаний х = Xm sin (ωt + ϕ0).

31.

32.

33.

34.

35.

36.

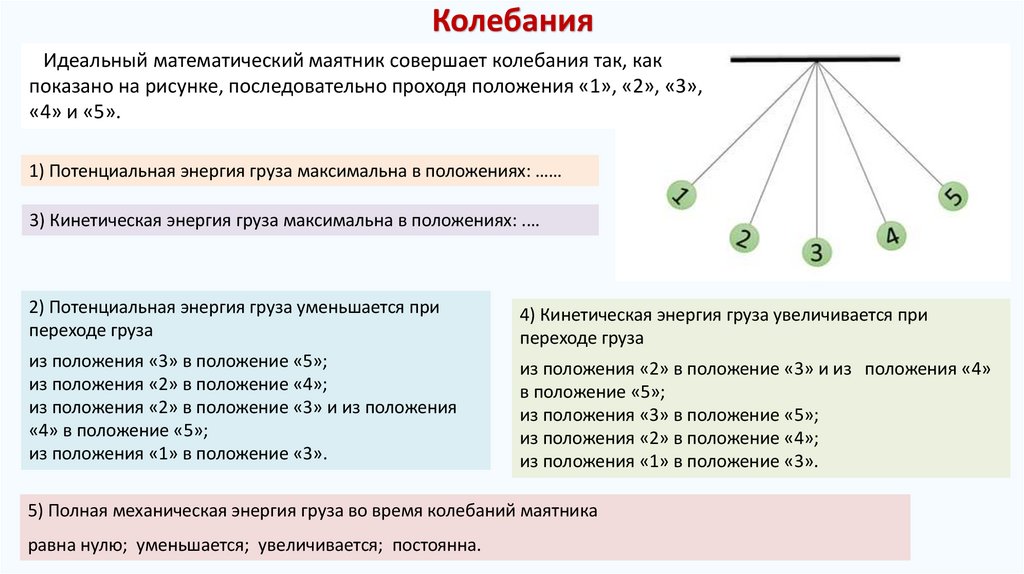
Колебания
Идеальный математический маятник совершает колебания так, как
показано на рисунке, последовательно проходя положения «1», «2», «3»,
«4» и «5».
1) Потенциальная энергия груза максимальна в положениях: ……
3) Кинетическая энергия груза максимальна в положениях: .…
2) Потенциальная энергия груза уменьшается при
переходе груза
4) Кинетическая энергия груза увеличивается при
переходе груза
из положения «3» в положение «5»;
из положения «2» в положение «4»;
из положения «2» в положение «3» и из положения
«4» в положение «5»;
из положения «1» в положение «3».
из положения «2» в положение «3» и из положения «4»
в положение «5»;
из положения «3» в положение «5»;
из положения «2» в положение «4»;
из положения «1» в положение «3».
5) Полная механическая энергия груза во время колебаний маятника
равна нулю; уменьшается; увеличивается; постоянна.

37.

Колебания
Изменится ли период колебаний качелей если вместо одного человека на них сядет двое?
Тело за 30 с совершило 150 колебаний. Чему равен период колебаний?
Найдите массу груза, который на пружине жесткостью 250 Н/м совершает 20 колебаний за 16 с?
Маятник часов совершает незатухающие гармонические колебания. Какие из величин — смещение,
амплитуда, период, частота, скорость, ускорение — являются постоянными и какие переменными?
В неподвижном лифте висит маятник, период колебания которого Т1=1 сек. С каким ускорением движется лифт,
если период колебаний этого маятника стал равным Т2=1,1 сек. В каком направлении движется лифт?
Влияет ли изменение температуры на точность хода маятниковых часов?
Пружинный маятник совершил за некоторое время 16 колебаний. Когда массу груза увеличили на 200 г,
маятник совершил за такое же время 15 колебаний. Какова начальная масса груза?