Лекция_4_5_Симплекс_и_двойственная

1.

Симплексный метод решения задач
линейного программирования
И
Теория двойственности в
землеустроительных задачах

2.

«Тема 4: Симплексный метод решения
задач линейного программирования»:
4.1. Идея симплекс-метода
4.2. Искусственный базис
4.3. Двойственные задачи линейного
программирования
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
2 | 33

3.

4.1. Идея симплекс-метода
Симплекс метод - это
метод последовательного
улучшения плана
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
3 | 35

4.

4.1. Идея симплекс-метода
Для решения задач линейного
программирования симплекс методом
необходимо систему неравенств
преобразовать в уравнения, где все свободные
члены неотрицательны.
При этом целевая функция стремится к
максимуму.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
4 | 35

5.

4.1. Идея симплекс-метода
Симплекс-метод применяется к
задачам, которые изначально
должны быть приведены к
каноническому виду.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
5 | 35

6.

4.1. Идея симплекс-метода
Для того, чтобы неравенства привести к форме уравнений,
необходимо к левой части каждого неравенства прибавить
балансирующую переменную, которую еще называют
базисной.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
6 | 35

7.

4.1. Идея симплекс-метода
Количество введенных базисных переменных
должно совпадать с количеством ограничений в
задаче.
Если в неравенстве стоит знак « ≥ », то базисная
переменная вводится со знаком « – ».
Если в неравенстве стоит знак « ≤ », то базисная
переменная вводится со знаком « + ».
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
7 | 35

8.

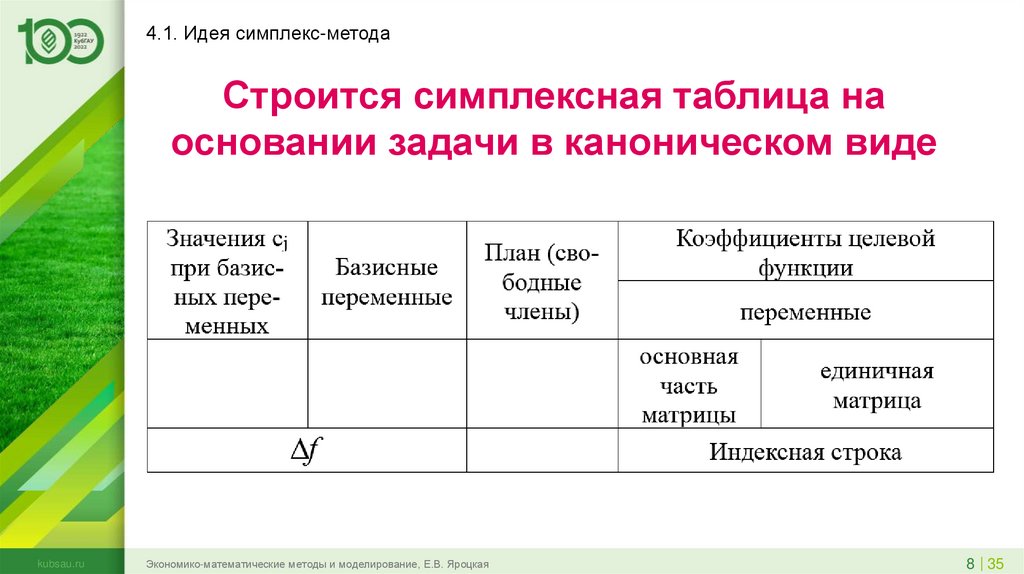
4.1. Идея симплекс-метода
Строится симплексная таблица на
основании задачи в каноническом виде
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
8 | 35

9.

4.1. Идея симплекс-метода
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
9 | 35

10.

4.1. Идея симплекс-метода
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
10 | 35

11.

4.1. Идея симплекс-метода
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
11 | 35

12.

4.1. Идея симплекс-метода
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
12 | 35

13.

4.1. Идея симплекс-метода
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
13 | 35

14.

4.1. Идея симплекс-метода
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
14 | 35

15.

4.1. Идея симплекс-метода
Индексы из целевой
строки с
противоположным
знаком
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
15 | 35

16.

4.1. Идея симплекс-метода
Канонический вид задачи линейного программирования
Симплексная таблица
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
16 | 35

17.

4.1. Идея симплекс-метода
В целевой строке записываются коэффициенты
при переменных целевой функции.
В строке переменных записываются символы,
которыми обозначены переменные (х1,х2…хj…хn).
Переменные записывают со своими индексами
Индексная строка указывает, в каком
направлении следует улучшать программу и когда
получается оптимальный план.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
17 | 35

18.

4.1. Идея симплекс-метода
В столбце Сi записываются коэффициенты при
переменных из индексной строки, вошедших в базис.
В столбце «Базис» записывают переменные,
введенные в базис со своими индексами.
Столбец свободных членов содержит константы,
правые части ограничений.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
18 | 35

19.

4.1. Идея симплекс-метода
Основная часть матрицы
• состоит из элементов аij, их называют техникоэкономическими коэффициентами.
Единичная матрица
• образуется из коэффициентов при
дополнительных (базисных) переменных.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
19 | 35

20.

4.1. Идея симплекс-метода
Алгоритм симплекс-метода
kubsau.ru
1.
• Заполняется исходная симплексная таблица
2.
• После получения опорного плана просматриваются
коэффициенты индексной строки (если все они
неотрицательны, и решается задача на максимум, то
оптимальное решение достигнуто)
3.
• Если в индексной строке есть отрицательный
коэффициент и решается задача на максимум, то план
неоптимальный и его необходимо улучшить
Экономико-математические методы и моделирование, Е.В. Яроцкая
20 | 35

21.

4.1. Идея симплекс-метода
Алгоритм симплекс-метода
Улучшение опорного плана
Просматриваются отрицательные коэффициенты индексной строки и
выбирается тот, абсолютное значение которого наибольшее. Данный
коэффициент укажет на ключевой столбец.
Определяется ключевая строка по наименьшему симплексному
отношению, то есть ключевого столбца
и выбирается наименьшее из них.
Наименьшее симплексное отношение укажет на ключевую строку, а на
пересечении ключевого столбца и ключевой строки будет находиться ключевой
элемент.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
21 | 35

22.

4.1. Идея симплекс-метода
Алгоритм симплекс-метода
kubsau.ru
4.
• Чертится новая симплексная таблица,
заполнение которой начинается с начальной
строки (ключевая в предыдущей таблице)
5.
• В базис вводится новая переменная, а одна
переменная из базиса удаляется.
Экономико-математические методы и моделирование, Е.В. Яроцкая
22 | 35

23.

4.1. Идея симплекс-метода
Алгоритм симплекс-метода
6.
kubsau.ru
• Заполняются все другие строки таблицы,
включая индексную по правилу
треугольника
Экономико-математические методы и моделирование, Е.В. Яроцкая
23 | 35

24.

4.1. Идея симплекс-метода
7.
kubsau.ru
• После расчета всех элементов
новой таблицы план проверяется на
оптимальность.
• Если план неоптимальный,
выполняется пункт 3 алгоритма до
получения оптимального плана.
Экономико-математические методы и моделирование, Е.В. Яроцкая
24 | 35

25.

4.1. Идея симплекс-метода
Признаки оптимальности плана
в задачах на
максимум (max)
в задачах на
минимум (min)
• все коэффициенты индексной строки
должны быть положительны
• все коэффициенты индексной строки
должны быть отрицательны
Если хотя бы один коэффициент индексной строки не
удовлетворяет этим условиям – план не оптимален.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
25 | 35

26.

4.2. Искусственный базис
Данный метод применяется в задачах имеющих
ограничения ≥ и =.
Поскольку левая часть больше правой,
дополнительная переменная вводится со знаком
минус. В каждое уравнение, заданное условием
задачи или имеющее дополнительную переменную
со знаком минус, вводят искусственные
переменные с положительными коэффициентами.
Численно они равны нулю
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
26| 35

27.

4.2. Искусственный базис
В симплексной таблице добавляется еще одна
индексная строка с М - оценками. Чтобы
искусственные переменные не вошли в решение
их вводят в целевую функцию с очень большим
коэффициентом М. При решении задач на max
коэффициент М вводят со знаком минус, при
решении задач на min - с плюсом.
Из-за использования числа М, метод вошел в
литературу под названием М-метода.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
27 | 35

28.

4.2. Искусственный базис
Модель М – задачи:
Дополнительная индексная строка с М-оценками численно определяется,
как сумма коэффициентов столбца умноженных на М. Оптимальный план
находится симплексным методом.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
28 | 35

29.

4.3. Двойственные задачи линейного программирования
Любой прямой задаче линейного
программирования противостоит
двойственная задача,
непосредственно вытекающая из
первой.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
29 | 35

30.

4.3. Двойственные задачи линейного программирования
Прямая задача
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
Двойственная задача
30 | 35

31.

4.3. Двойственные задачи линейного программирования
Прямая задача
линейного
программирования
F ( x) 45 x1 43,7 x2 13,35 x3 max
х1 x2 x3 320
19 х1 15 х2 10 х3 5000
40 х 30 х 48 х 19200
2
3
1
x j 0, j 1,3
Двойственная
задача линейного
программирования
L( y ) 320 y1 5000 y2 19200 y3 min
y1 19 y2 40 y3 45
y1 15 y2 30 y3 43,7
y 10 y 48 y 13,35
2
3
1
yi 0, i 1,3
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
31 | 35

32.

4.3. Двойственные задачи линейного программирования
Экономический смысл:
Прямая задача
Найти сколько и какой
продукции необходимо
произвести, чтобы при
заданных ценах и размерах
производственных ресурсов
максимизировать выпуск
продукции в стоимостном
выражении.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
Двойственная задача
Какова должна быть цена
единицы каждого ресурса,
чтобы при заданных
количествах ресурсов Bi и
величинах стоимости
единицы продукции Cj
минимизировать стоимость
затрат.
32 | 35

33.

4.3. Двойственные задачи линейного программирования
Каждая из задач двойственной пары
является самостоятельной задачей,
может решаться самостоятельно
одна от другой. Деление на исходную
и двойственную условно в том
смысле, что любая из задач может
быть исходной.
kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
33 | 35

34.

kubsau.ru
Экономико-математические методы и моделирование, Е.В. Яроцкая
7 | 33

35.

Яроцкая Елена Вадимовна
Заведующая кафедрой землеустройства
и земельного кадастра,
к.э.н., профессор
+7 (861) 221-59-46
Jarockaja.E@kubsau.ru
kubsau.ru