Модуль 1. Обзор

1. Численные методы

Модуль 1

2. План

1. Введение
2. Погрешности
3. Решение уравнений
4. Решение систем

3. Численные методы

– это методы приближенного решения задач на ЭВМ, которые не
могут быть решены аналитическим способом (точно) или их
решение требует слишком больших затрат.

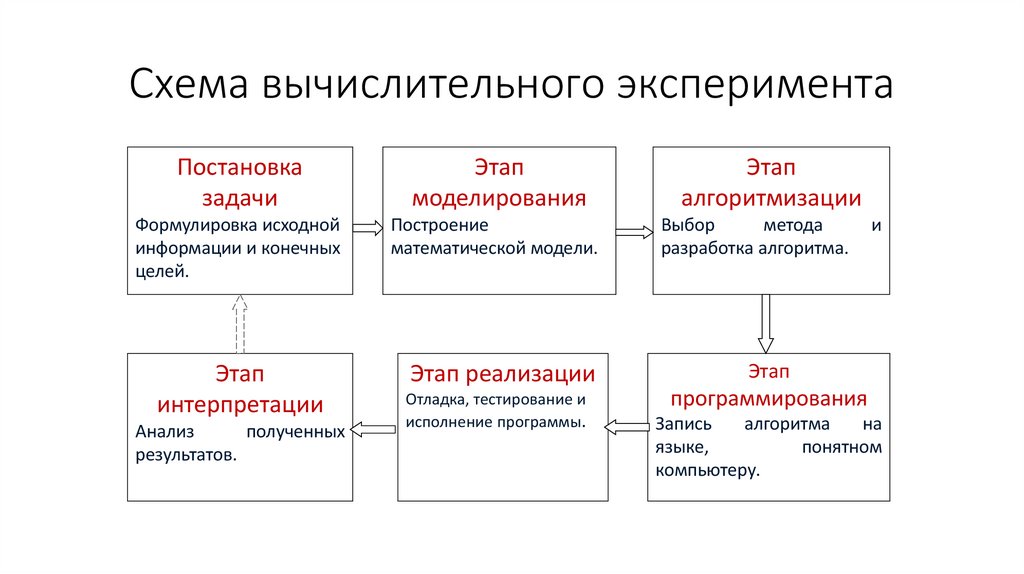
4. Схема вычислительного эксперимента

Постановка
задачи
Этап
моделирования
Этап
алгоритмизации
Формулировка исходной
информации и конечных
целей.
Построение
математической модели.
Выбор
метода
разработка алгоритма.
Этап
интерпретации
Этап реализации
Анализ
полученных
результатов.
Отладка, тестирование и
исполнение программы.
и
Этап
программирования
Запись
алгоритма
на
языке,
понятном
компьютеру.

5. Структура погрешности

• Погрешность исходных данных (неустранимая).
• Погрешность модели.
• Погрешность метода.
• Вычислительная погрешность.

6. Корректность

Задача называется корректно поставленной, если для
любых значений исходных данных из некоторого
допустимого множества ее решение существует,
единственно и устойчиво по начальным данным.

7. Устойчивость

Устойчивость по начальным данным означает, что малым
изменениям исходных данных соответствует незначительное
изменение результата (в применении к устойчивым реальным
процессам).
Устойчивость метода трактуется аналогично – малым ошибкам
округления соответствует малые изменения результата.

8. Сходимость

Численный метод сходится к точному решению задачи,
если при неограниченном росте параметра
дискретизации решение дискретной задачи
стремиться к решению исходной задачи.
Необходимость получения результата с любой заранее
заданной точностью за конечное число шагов требует
использования быстро сходящихся методов.

9. Абсолютная погрешность

Пусть X – точное значение некоторой величины (обычно неизвестное),
– число, принятое за ее приближенное значение (X x).
Предельной абсолютной погрешностью, являющейся верхней
границей, называют такое по возможности наименьшее число, для
которого справедливо неравенство:
x |X – x|

10. Относительная погрешность

Предельная относительная погрешность приближенного
числа – это отношение предельной абсолютной
погрешности к абсолютному значению приближения:
x
x
x
Относительную погрешность обычно выражают в процентах.

11. Границы точного результата

Опр. Любая пара чисел НГх и ВГх, такая, что НГх ≤ х ≤ ВГх
называется нижней и верхней границей приближенного числа х.
Если известны х и Δх , то принято записывать:
X [ х x , х x ]
или
X x x

12. Значащие цифры

Определение. Все цифры десятичной записи числа, начиная с
первой ненулевой слева, называются значащими.
• 308,6170 – 7 значащих цифр
• 0,00235 – 3 значащих цифры
• 57 000 – 5 з.ц., 5,7*104 – 2 з.ц., 570*102 – 3 з.ц.

13. Округление чисел

Определение: округлением числа называют замену его
близким по величине, но с меньшим количеством
значащих цифр.
Различают 3 вида округления:
Симметричное округление – к ближайшему числу:
3,6≈4; 3,67≈3,7; 3,4≈3; 3,42≈3,4
С избытком - к большему числу: 3,6≈4; 3,2≈4
С недостатком - к меньшему числу (округление
отсечением): 3,67≈3,6; 3,2≈3.

14. Округление погрешностей

Правило:
В записи погрешности обычно оставляют только 1-2
значащие цифры.
Для сохранения условия, соответствующего определению
предельной погрешности, округление её всегда
производят с избытком.
Это правило распространяется как на абсолютную, так и на
относительную погрешности.

15. Верные цифры

Определение. Цифра в записи числа а, называется верной, если
погрешность не превосходит единицы её разряда; цифра верная
в строгом смысле - если погрешность не превосходит половины
её разряда.

16. x=72,256 Δх= 0,01

а) Решение:
2: 0.1 ≥ 0.01 - верная
5: 0.01= 0.01 – верная
6: 0.001≤ 0.01 - сомн.
Ответ: верные в широком
смысле цифры 7;2;2;5
а 6 - сомнительная
б) Решение:
2: 0.05 ≥ 0.01 - верная
5: 0.005 ≤ 0.01 – сомн.
Ответ: верные в строгом
смысле цифры 7;2;2
а 5 и 6 - сомнительные

17. Запись приближённых чисел

Правило: в промежуточных результатах вычислений
обычно сохраняют 1-2 сомнительные цифры, а
окончательные результаты округляют с сохранением не
более одной сомнительной цифры.

18. Оценка погрешности вычисления функции

Определим, как вычислить погрешность функции, некоторые
аргументы которой заданы приближенно.
Задачу нахождения погрешности функции по заданным
погрешностям приближенных аргументов называют основной
задачей теории погрешностей.

19. Оценка погрешности по способу границ

Пусть y=f(x) - функция, для которой необходимо найти
погрешность, a - приближенное исходное данное и известны НГа и
ВГа.
Необходимо определить y=f(x), НГу и ВГу.
Для нахождения границ результата вычисляют y1=f(НГx) и y2=f(ВГx),
а затем меньшее из этих значений принимают за НГy, а большее за
ВГy и округляют нижнее с недостатком, а верхнее с избытком.

20. Пример:

ex
y
1 x2
Пример:
1, 25 x 1, 28,
Решение.
e1,25
y ( НГ х )
1,3620849...
2
1 1,25
НГy =1.362
e1,28
y ( ВГ х )
1,3631896...
2
1 1,28
ВГy =1.364
y
ВГ y НГ y
2
1,364 1,362
0,001
2
y
y 1,363 0, 001
ВГ y НГ y
2
1,363

21. Дифференциальная оценка погрешности

Замечание. При малых значениях Δx и Δy можно вместо
максимумов частных производных в прямоугольнике брать
значения производных с приближенными значениями
аргументов:
z f x ( x, y ) x f y ( x, y ) y .

22.

f(x,y)= x2+sin y
f
2 x,
x
f
cos( y ).
y
z 2 ( 0,68) 0,004 cos(1,134) 0,003 0,00556691163...
0,006
z ( 0,68)2 sin(1,134) 1,368511588...
z 1,37 0,006.
0,006
0,004379562...
1,37
1,37
0,0044 0,44%

23. Обратная задача теории погрешностей

Обратная задача теории погрешностей состоит в том, что по
заданной абсолютной погрешности функции необходимо
определить, каковы должны быть абсолютные погрешности ее
аргументов.

24. Обратная задача теории погрешностей

Одна и та же суммарная оценка погрешности
функции нескольких аргументов, вычисляемая,
например, дифференциальным способом, может
быть получена при различных распределениях
погрешностей аргументов.
f
f
xi .
i 1 xi
n

25. Обратная задача теории погрешностей

Для решения обратной задачи обычно
пользуются принципом «равных
влияний»:
f
f
xi , т.е. все слагаемые оценки равны.
n
xi
Тогда
f f
xi
/
n xi

26. Решение нелинейных уравнений

Дана функция f (x) непрерывная на некотором промежутке [a;b].
Надо: найти корни уравнения
f (x) =0 (1) с заданной точностью .
• 1 этап
Отделить корни – это значит указать промежуток [a, b] ,
содержащий один и только один корень уравнения (1). Иначе
говорят: указать отрезки изоляции корней.
Способы отделения: аналитический, графический, табличный.

27. Итерационные методы

2 этап. После того, как корни локализованы, задача сводится к
уточнению корня уравнения f (x) =0 на промежутке [a;b] с
заданной точностью .
В итерационных методах для этого строится последовательность:
x0, x1, x2, …, xi, … ,
сходящаяся к точному решению x*.

28. Типы сходимостей итерационных последовательностей

Скоростью сходимости итерационного метода называется
скорость убывания величины |x*-xi|.
Если |x*-xi+1|≤ q |x*-xi|, то имеет место линейная
сходимость.
Если |x*-xi+1|≤ q |x*-xi|α, 1<α<2, то имеет место
сверхлинейная сходимость.
Если |x*-xi+1|≤ q |x*-xi|2, то имеет место квадратичная
сходимость.

29. Достижение точности

Применяя итерационный метод, получаем
последовательность x1,x2,x3,…xi,…, сходящуюся к точному
решению уравнения.
Возникает вопрос, какой из элементов этой
последовательности принять за приближенное значение с
точностью и прекратить итерационный процесс уточнения
корня?

30. Оценка точности приближения

может характеризоваться следующими величинами:
Невязка f (xi)
Ошибка
x*- xi
Поправка xi+1 - xi
Любая из этих величин может учитываться в условии
окончания итерационного процесса приближения к
корню.

31.

y
f (b)
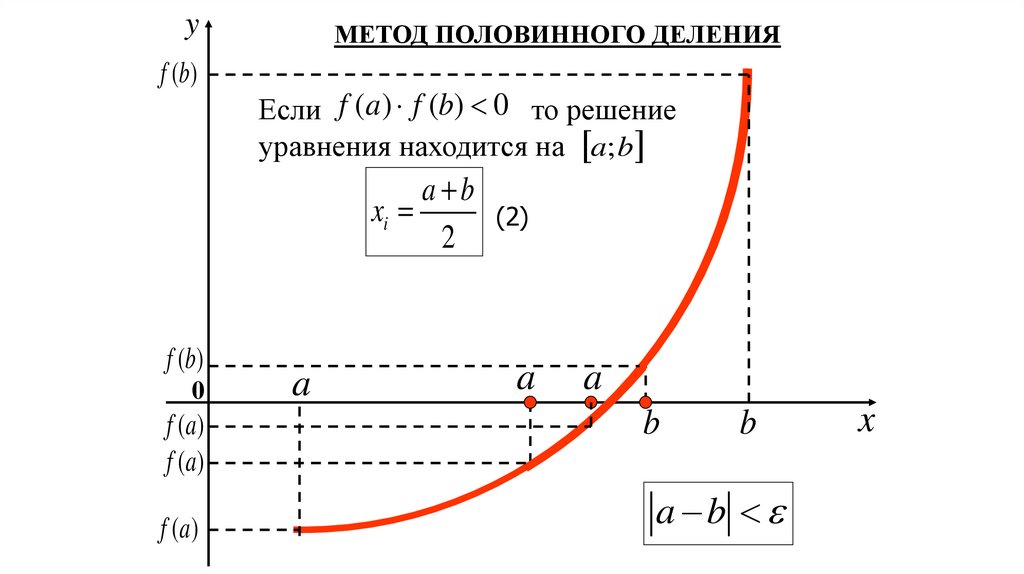
МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ
Если f (a) f (b) 0 то решение
уравнения находится на a; b
a b
xi
(2)
2
f (b)
0
f (a)
f (a)
f (a)
a
a
a
b
b
a b
x

32.

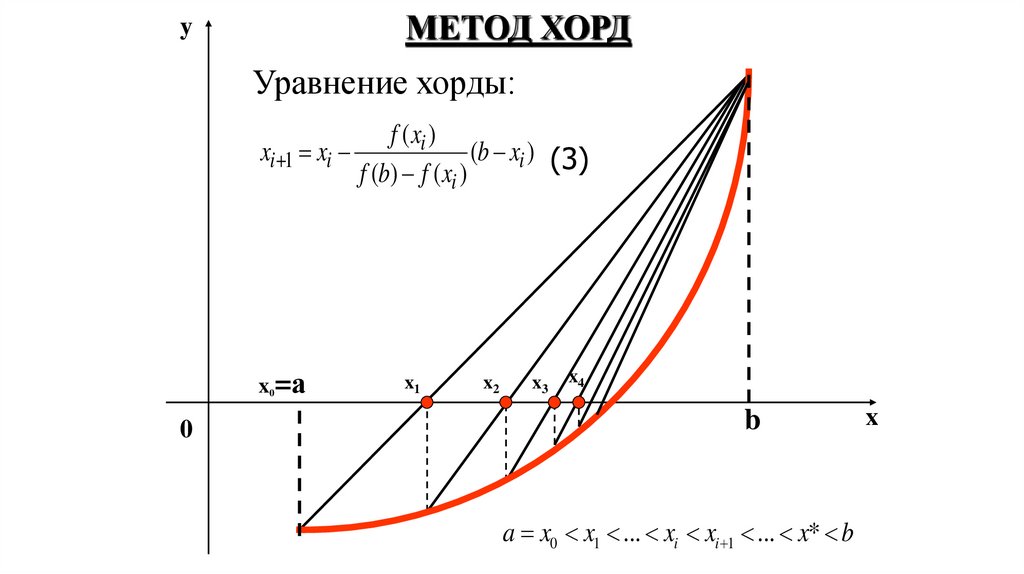
МЕТОД ХОРД
y
Уравнение хорды:
f ( xi )
xi 1 xi
(b xi ) (3)
f (b) f ( xi )
x0=а
0
x1
x2
x3
x4
b
a x0 x1 ... xi xi 1 ... x* b
x

33.

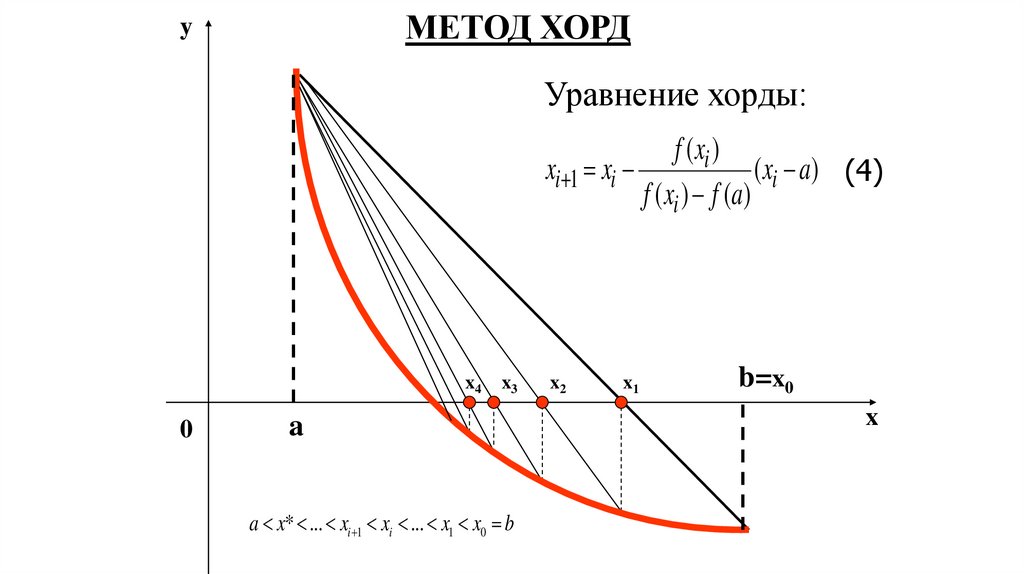
МЕТОД ХОРД
y
Уравнение хорды:
f ( xi )
xi 1 xi
( xi a) (4)
f ( xi ) f (a)
x4
0
x3
a
a x* ... xi 1 xi ... x1 x0 b
x2
x1
b=x0
x

34.

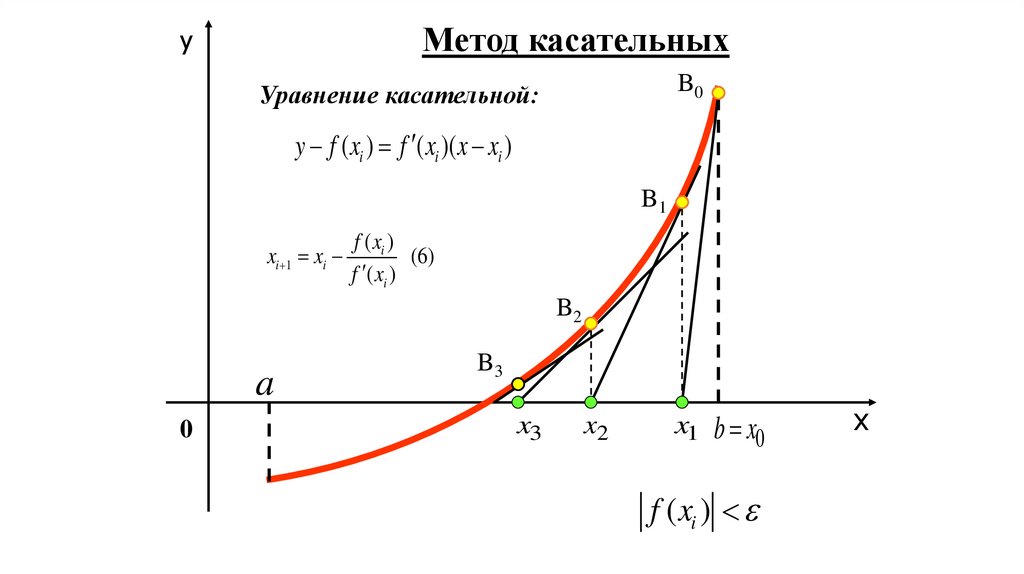
Метод касательных
y
B0
Уравнение касательной:
y f ( xi ) f ( xi )( x xi )
B1
xi 1 xi
f ( xi )
(6)
f ( xi )
B2
a
0
B3
x3
x2
x1 b x
0
f ( xi )
x

35. Метод секущих

– это упрощение метода касательных, когда затруднительно
найти производную. Заменим в методе касательных
производную конечно-разностным отношением:
f ( xi ) f ( xi 1 )
f ' ( xi )
xi xi 1
xi xi 1
xi 1 xi
f ( xi ) (8)
f ( xi ) f ( xi 1 )

36. Метод простой итерации

Рассмотренные методы решения уравнения f(x)=0 сводились к
итерационной процедуре вида
xi+1=φ(xi) (9)
Основная идея метода простой итерации состоит в том, чтобы
построить универсальный метод типа (9).
Условие сходимости:
' ( ) 1

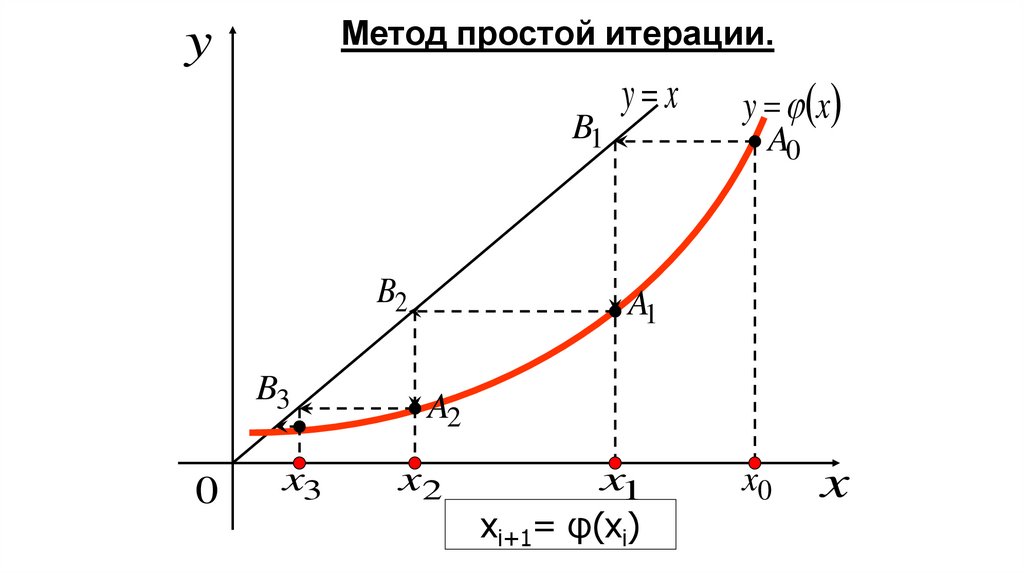
37.

Метод простой итерации.
y
B1
B2
B3
0
x3
y x
y x
A0
A1
A2
x2
x1
xi+1= φ(xi)
x0
x

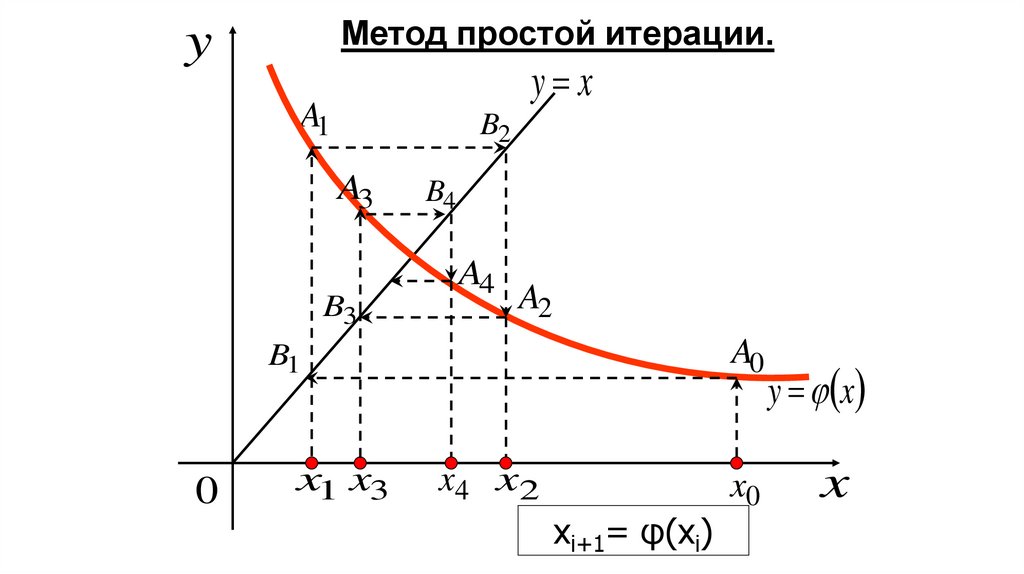
38.

Метод простой итерации.
y
y x
A1
B2
A3
B3
B4
A4
A2
B1
0
x1 x3
x4 x2
xi+1= φ(xi)
A0
y x
x0
x

39. Упражнение. На отрезке [1;2] привести к итерационному виду уравнение x4-2x-3=0.

Производная
f’(x)=4x3-2 на [1;2] монотонно
возрастает:
m1= f’(1)=2
M1= f’(2)=30.
λ=2/(M1+ m1)
λ=2/(30+ 2)=1/16
φ(x)= x- λ*f(x)
x = x – (x4-2x-3)/16
3
’ = 1 – (2x3-1)/8
2
1
f(x)
0
0
-1
-2
-3
0,5
1
1,5
2
2,5
3
fi'(x)

40. Методы решения нелинейных уравнений

Метод
Скорость сходимости
половинного деления
линейная
хорд
линейная
касательных
квадратичная
секущих (хордкасательных)
сверхлинейная
простой итерации
Линейная/
квадратичная

41. Методы решения СЛАУ

1. Прямые (точные) методы: решение находится за конечное
число арифметических действий. Точными их можно
назвать лишь абстрагируясь от погрешностей округления.
2. Итерационные методы состоят в том, что решение системы
(1) определяется как предел некоторой
последовательности приближений X k при k , где k –
номер итерации.
3. Вероятностные методы или методы Монте-Карло
используют для решения систем с очень большим числом
неизвестных (>107).

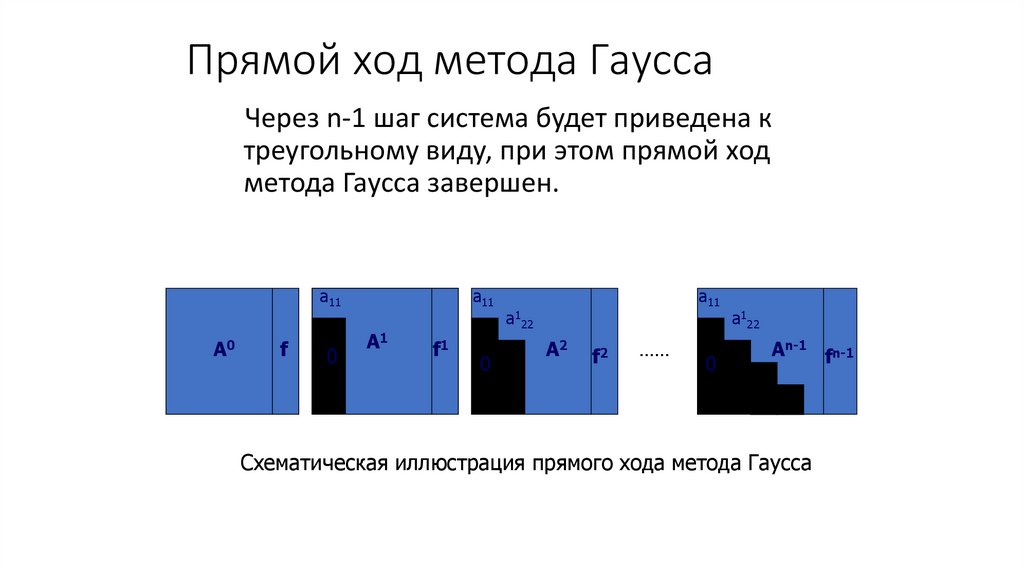
42. Прямой ход метода Гаусса

Через n-1 шаг система будет приведена к
треугольному виду, при этом прямой ход
метода Гаусса завершен.
a11
A0
f
0
0
b A1
a11
f1
00
a11
a122
A2
f2
……
00
a122
An-1 fn-1
Схематическая иллюстрация прямого хода метода Гаусса

43. Обратный ход метода Гаусса

Осуществляется для нахождения неизвестных системы.
Из последнего уравнения находится xn. Его значение подставляется
в n-1 уравнение …
и т. д. до первого уравнения и х1.

44. Пример. Метод Гаусса (со схемой единственного деления*)

2 3 1 3
3 2 4 13
4 1 2 7
3
1
1 2
2
0 1 11
13
0 5 4
3
2
35
13
13
3
1
2
3 2
4 1
1 3
2
2
4 13
2
7
3
1 2
0 1
0 0
1
2
11
13
3
13
3
2
35
13
6
13
1
0
0
3
2
13
2
5
3
1
2
0 1
0 0
1 3
2
2
11 35
2
2
4 13
1
2
11
13
1
3
2
35
13
2
* Схема единственного деления применяется для получения 1 на диагонали путем деления на
разрешающий элемент

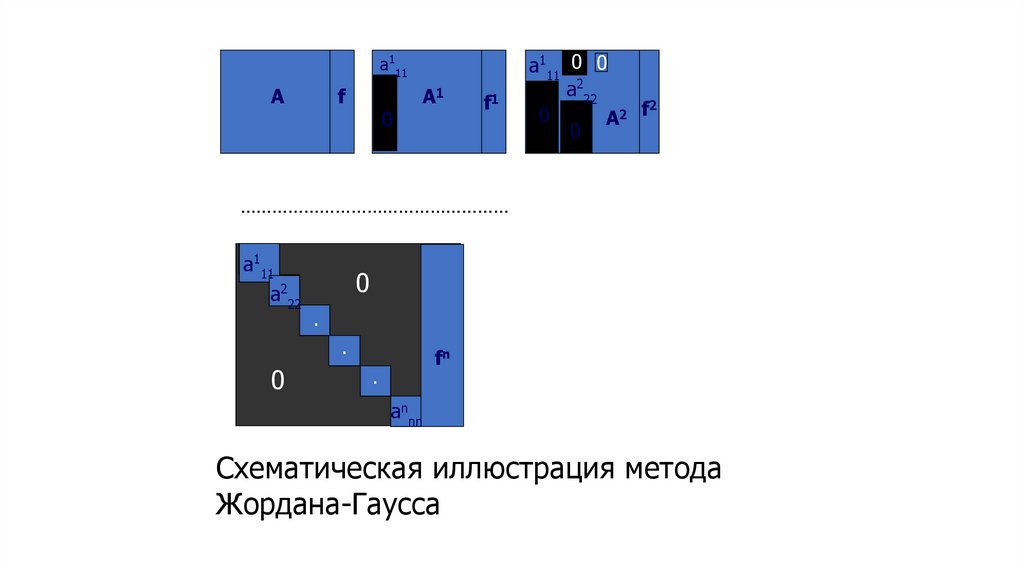
45.

a111
A
f
0
A1
f1
a111 0 0
a222
2
0
A2 f
0
……………………………………………
a111
a222
0
.
.
0
fn
.
annn
Схематическая иллюстрация метода
Жордана-Гаусса

46. Пример. Метод Жордана-Гаусса (схема единственного деления)

2 3 1 3
3 2 4 13
4 1 2 7
3
1
2
3 2
4 1
1 3
2
2
4 13
2
7
3
1
1 2
2
0 1 11
13
0 5 4
1 0
0 1
0 0
10
13
11
13
3
13
3
2
35
13
13
33
13
35
13
6
13
1
0
0
3
2
13
2
5
1 3
2
2
11 35
2
2
4 13
1 0 0 1
0 1 0 1
0 0 1 2

47. Выбор главного элемента осуществляется следующим образом:

переставим 2-ое и 3-е уравнения:
7
0 x1 7
10
0 0.001 6 x 6.001
2
0
2.5
5 x3 2.5
7
0 x1 7
10
0
x 2.5
2.5
5
2
0 0.001 6 x3 6.001
исключим х2 из 3-го уравнения:
0 x1 7
10 7
0 2.5
x 2.5
5
2
0 0 6.002 x3 6.002

48. Обратный ход

6.002
x3
1
6.002
2.5 5 1
x2
1
2.5
7 7 ( 1)
x1
0
10
Результат совпадает с точным решением.

49. Виды норм

вектора:
X I max xi
i 1, n
матрицы:
кубическая
n
A I max aij
i 1, n
j 1
n
n
X II xi
октаэдрическая
A II max aij
j 1, n
i 1
X III
n
x
i 1
i
2
сферическая
A III
i 1
n
n
a
i 1 j 1
ij
2

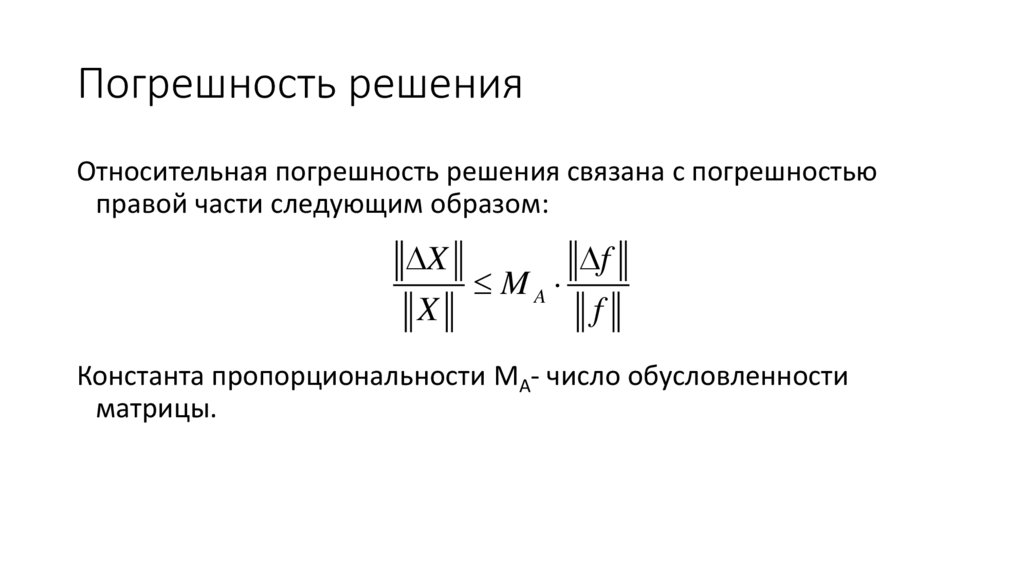
50. Погрешность решения

Относительная погрешность решения связана с погрешностью
правой части следующим образом:
X
f
MA
X
f
Константа пропорциональности MA- число обусловленности
матрицы.

51. Приведение системы к итерационному виду

Для этого систему (1) переписываем в виде,
удобном для итерационного процесса:
x1 11x1 12 x2 ... 1n xn 1
x x x ... x
2
21 1
22 2
2n n
2
(2) .....................................................
xn n1 x1 n 2 x2 ... nn xn n
В матричном
виде:
X aX

52. Способ 1. Поделив каждое уравнение на соответствующий диагональный элемент (если они не равны нулю) и решив уравнения

Приведение системы к итерационному виду
Способ 1. Поделив каждое уравнение на соответствующий
диагональный элемент (если они не равны нулю) и решив
уравнения относительно диагональных переменных, получим:
5 x1 x 2 x3 4
0,5 x1 2 x 2 x3 1
x x 4x 2
2
3
1
x1 0,2 x 2 0,2 x3 0,8
x 2 0,25 x1 0,5 x3 0,5 (*)
x 0,25 x 0,25 x 0,5
1
2
3

53. Метод простой итерации

Итерационные методы различаются только по способу построения
последовательности.
Формулы метода простой итерации:
X
X
(1)
(2)
X
(0)
X
(1)
..........................
X
( k 1)
X (k )
( k 1)
i
x
n
ij x(jk ) i , i 1,..., n; k 0,1,...
j 1

54. Метод Зейделя

(