Похожие презентации:
Численное решение алгебраических и трансцендентных уравнений
1. Тема 2 Численное решение алгебраических и трансцендентных уравнений.
Тема 2Численное решение алгебраических и
трансцендентных уравнений.
2.1. Отделение корней нелинейного уравнения.
2.2. Алгоритмы уточнения корней уравнения.(Метод
дихотомии (половинного деления, бисекций). Метод
простых итераций (метод последовательных
приближений). Метод хорд. Метод Ньютона
(касательных).
1
2.
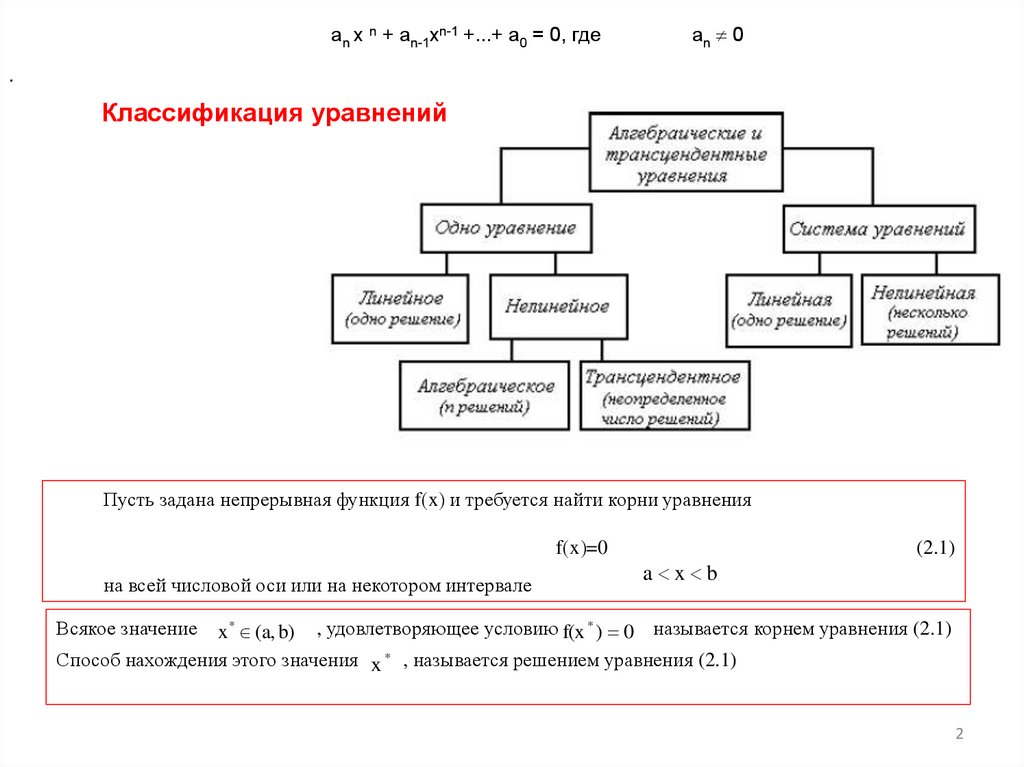
an x n + an-1xn-1 +...+ a0 = 0, гдеan 0
.
Классификация уравнений
Пусть задана непрерывная функция f x и требуется найти корни уравнения
f x =0
на всей числовой оси или на некотором интервале
(2.1)
a x b
Всякое значение
x * (a, b) , удовлетворяющее условию f(x * ) 0 называется корнем уравнения (2.1)
Способ нахождения этого значения x * , называется решением уравнения (2.1)
2
3.
Методы решенияуравнений
Этапы численного
решения уравнений
Прямые
Итерационные
1 этап.
Отделение корней уравнения.
Аналитические методы
2 этап.
Уточнение интересующих корней с заданной точностью ε.
Метод дихотомии
Графические методы
Метод простых итераций
Метод хорд
Метод Ньютона
3
4.
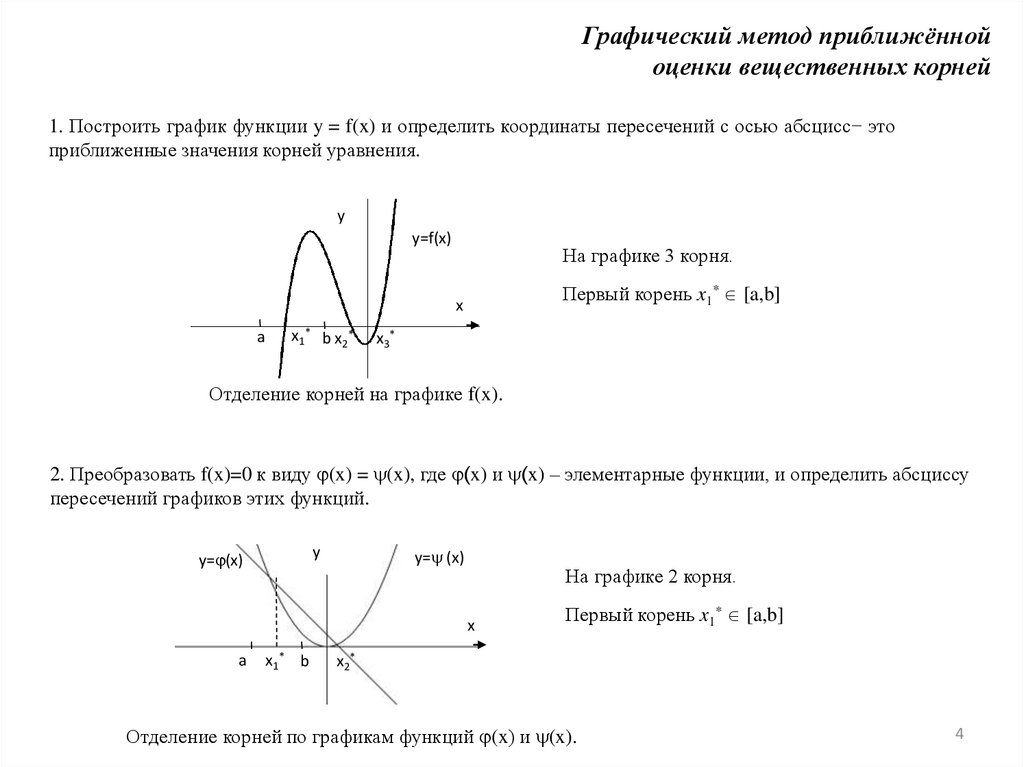
Графический метод приближённойоценки вещественных корней
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это
приближенные значения корней уравнения.
y
y=f(x)
На графике 3 корня.
Первый корень x1* [a,b]
x
a
x1* b x2*
x3*
Отделение корней на графике f(x).
2. Преобразовать f(x)=0 к виду (x) = (x), где (x) и (x) – элементарные функции, и определить абсциссу
пересечений графиков этих функций.
y
y= (x)
y= (x)
На графике 2 корня.
x
a
x1* b
Первый корень x1* [a,b]
x2*
Отделение корней по графикам функций (x) и (x).
4
5.
56.
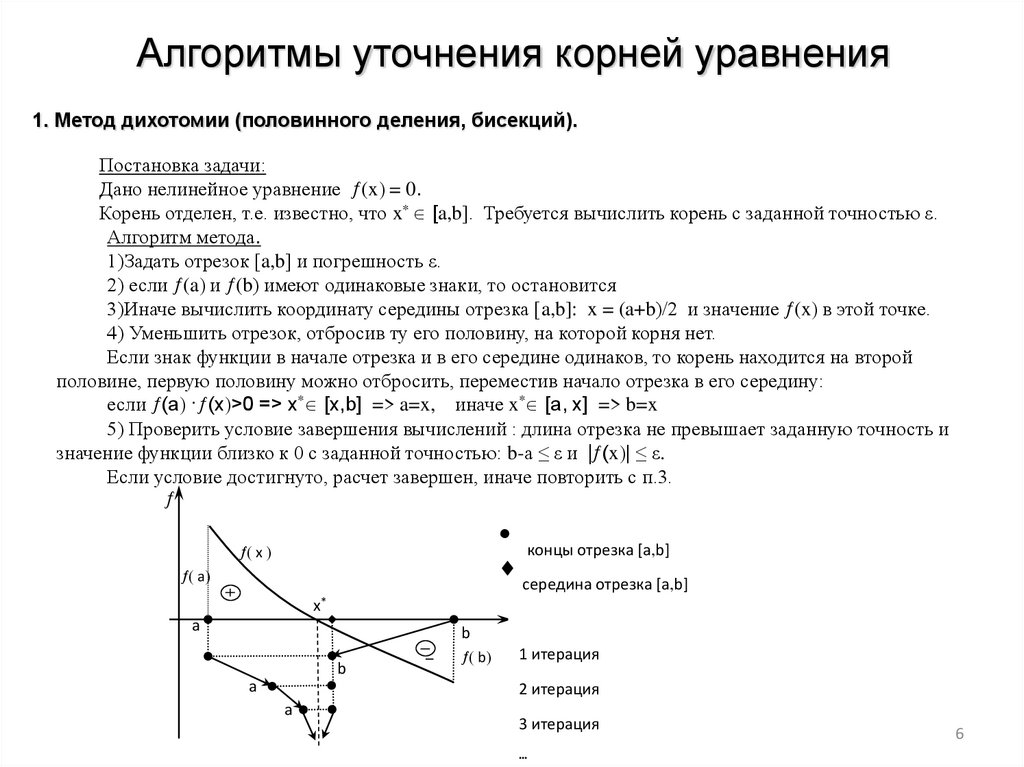
Алгоритмы уточнения корней уравнения1. Метод дихотомии (половинного деления, бисекций).
Постановка задачи:
Дано нелинейное уравнение (x = 0.
Корень отделен, т.е. известно, что x* [a,b]. Требуется вычислить корень с заданной точностью ε.
Алгоритм метода.
1)Задать отрезок [a,b] и погрешность ε.
2) если (a и (b) имеют одинаковые знаки, то остановится
3)Иначе вычислить координату середины отрезка [a,b]: x = (a+b)/2 и значение (x в этой точке.
4) Уменьшить отрезок, отбросив ту его половину, на которой корня нет.
Если знак функции в начале отрезка и в его середине одинаков, то корень находится на второй
половине, первую половину можно отбросить, переместив начало отрезка в его середину:
если (a · (x >0 => x* [x,b] => a=x, иначе x* [a, x] => b=x
5) Проверить условие завершения вычислений : длина отрезка не превышает заданную точность и
значение функции близко к 0 с заданной точностью: b-a ≤ ε и | (x | ≤ ε.
Если условие достигнуто, расчет завершен, иначе повторить с п.3.
концы отрезка [a,b]
x
a
середина отрезка [a,b]
x*
a
b
b
a
–
b
1 итерация
2 итерация
a
3 итерация
...
6
7.
b an
2n
b a
ln
ln 2
(x
x*
0
x
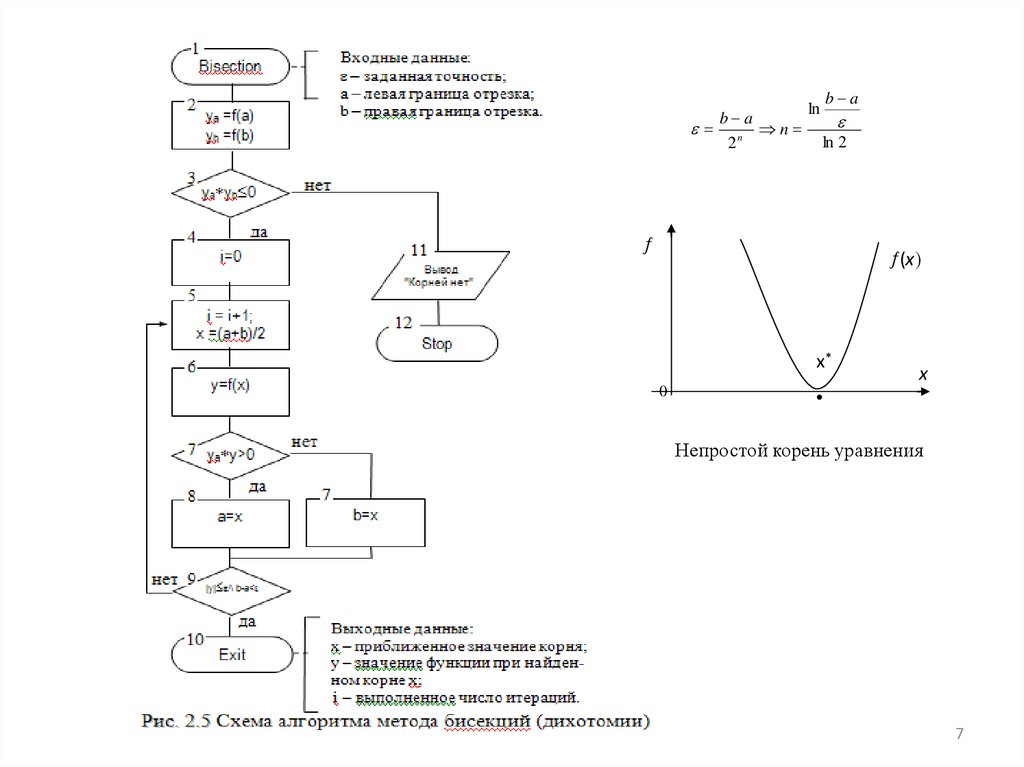
Непростой корень уравнения
7
8.
2. Метод простых итераций (метод последовательных приближений).Постановка задачи.
Дано нелинейное уравнение f x =0. Корень отделен x* [a;b].
Требуется уточнить корень с точностью ε.
Уравнение f x =0 преобразуем к эквивалентному виду
x=φ(x),
Выберем начальное приближение x0 [a;b].
Вычислим новые приближения:
x1=φ(x0)
x2=φ(x1)
………..
xi=φ(xi-1) , i=1,2,… где i − номер итерации.
(2.7)
(2.8)
Итерационный процесс сходящийся если lim xi x
*
i
Условие сходимости
(' x ) 1 x [a, b]
(2.9)
Условие завершения итерационного процесса
x * xi
8
9.
Итерационный процесс дляслучая
0 x' 1 x [a, b]
f x =0
y1=x
Y
y1 = x
y2= φ(x).
y2=φ(x)
φ(x0)
Итерационный процесс
φ(x1)
монотонно сходится
из любой точки [a,b]
X
a
x*
x2
x1
b=x0
Итерационный
процесс для случая
y1
Y
1 x' 1 x [a, b]
Итерационный процесс
колебательно (около
корня x*) сходится из
любой точки [a,b]
y2
Х
a=X0
X2 X*
X1
b
9
10.
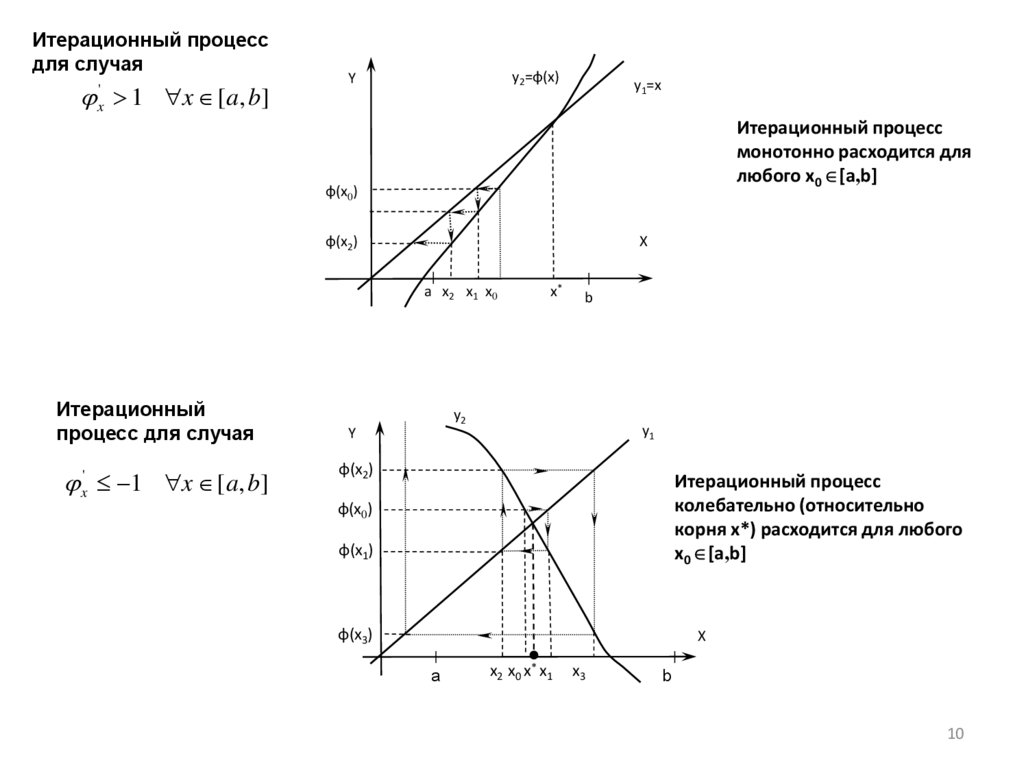
Итерационный процессдля случая
1 x [a, b]
'
x
y2=φ(x)
Y
y1=x
Итерационный процесс
монотонно расходится для
любого x0 [a,b]
φ(x0)
φ(x2)
Х
a x 2 x1 x0
Итерационный
процесс для случая
x' 1 x [a, b]
x*
b
y2
Y
y1
φ(x2)
Итерационный процесс
колебательно (относительно
корня x*) расходится для любого
x0 [a,b]
φ(x0)
φ(x1)
φ(x3)
Х
a
x2 x0 x* x1
x3
b
10
11.
Алгоритм решения нелинейного уравнения методом. простых итераций:
f(x) = 0 => x+f(x) = x, т.е. φ(x) = x + f(x)
1
Входные данные:
Iterations
2
– заданная точность;
imax– заданное число итераций;
i=0
f(x) = 0 => x - φ(x) = 0 => x = φ(x)
x0 – начальное значение корня.
Формулы сходящегося итерационного
процесса:
Пусть f ' ( x) 0 x [a, b] , иначе
3
f ( x) 0
I =i+1
x0=x
x x f ( x ) ( x )
4
x=φ(x0)
1
max f ' ( x)
x [ a ,b ]
нет
5
|x- x0|<
xi = xi-1− λ f(x)
i > imax
6
F= (x)
Выходные данные:
7
Выход
x – приближенное значение корня;
i – выполненное число итераций;
F – значение функции при найденном корне.
11
12.
3. Метод Ньютона (касательных).x1 = x0 − CB
Постановка задачи.
Дано нелинейное уравнение f(x)=0.
Корень отделен x* [a;b].
Требуется уточнить корень с точностью ε.
AB
Из ∆ABC: CB= tg ACB
Но
Геометрическая иллюстрация метода Ньютона
f
tg ACB f ' ( x0 ),
AB f ( x0 )
Следовательно,
x1 x0
f(x)
xi xi 1
f ( x0 )
f ' ( x0 )
f ( xi 1 )
, i 1,2,...
f ' ( xi 1 )
x [a;b].
0
A
Условие окончания расчета
x*
0
a
*
x
B
C
x1
x0
b
где
xi 1 xi
f ( xi 1 )
f ' ( xi 1 )
корректирующее приращение или поправка
Условие сходимости итерационного процесса:
f ( x) f ' ' ( x ) ( f ' ( x ) ) 2 x [a, b]
Условие выбора начального приближения,
обеспечивающего сходимость
f ( x0 ) f ' ' ( x0 ) 0 , x0 [a;b].
12
13.
ff(x)
a
0
x*
Геометрическая иллюстрация выбора
начального приближения: график f(x)
выпуклый, f ’’(x)<0 , тогда x0 =a, т.к. f(a)<0.
b x
x1
x0
Геометрическая иллюстрация выбора начального
приближения: график f(x) вогнутый, f ' ' ( x ) 0
тогда x0=b, т.к. f(b)>0.
f
f(x)
a
0
b
x
x*
13
14.
Схема алгоритма метода Ньютона1
2
fa=f(a)
3
да
44
Входные данные
a – левая граница отрезка;
b – правая граница отрезка;
– заданная точность.
imax –максимальное число итераций
Newton
f2a=f’’(a)
нет
fa· f2a>0
5
x=a
66
x=b
i=0
77
i=i+1
fx =f(x)
8 f1 =f ’(x)
x
9
нет
10
x=x-
i>imax U | |<ε∩|fx|≤ε
11
да
Выход
Выходные данные:
x – приближенное значение корня;
fx – значение функции при x;
– достигнутая точность;
i–количество выполненных итераций.
14









 Математика
Математика








