Похожие презентации:
4 ФНП24
1.
Раздел 4.Функции нескольких переменных
§ 1. Основные понятия и примеры
функций нескольких переменных
2.
Пусть X R n , Z R..Замечание. Напомним: R n {( x1; x2 ; ...; xn ) : xi R,1 i n} ;
( R2 – множество точек плоскости, R3 – множество точек
пространства).
Опр. 1. Если каждому набору значений n переменных величин
( x1; x2 ; ...; xn ) из некоторого множества X поставлено в соответствие
определенное число z Z , то говорят, что на множестве X задана
функция n переменных z f ( x1; x2 ; ...; xn );
здесь x1, x2 , ..., xn – независимые переменны (аргументы),
z – зависимая переменная (функция),
множество X – область определения,
множество Z – область
значений функции.
2
Пример 1. 1) z x1 x2 зависимость объема цилиндра
от радиуса основания x1 и высоты x2 .
2) z x12 x22 x32 зависимость длины вектора от значений его координат.
2
3.
3) z x 2 y 2Область определения X R2 ;
область значений Z [0; ).
Функция задает эллиптический параболоид.
4) z 1 x 2 y 2 .
Область определения: x 2 y 2 1;
область значений: Z [0;1].
График?
z 2 1 x2 y 2 ;
x 2 y 2 z 2 1.
сфера радиуса 1 с центром в начале координат
z 1 x2 y 2 0
верхняя половина сферы
3
4.
Мы рассмотрим основные понятия ФНП на примере функций двухпеременных (Ф2П), поскольку на случай функций 3-х и более переменных все
результаты могут быть обобщены без существенных измерений.
Опр. 2. Линией уровня Ф2П z f ( x; y ) называется множество
точек плоскости, в которых функция принимает одно и то же
значение c, т. е. f ( x; y) c.
Пример 2. z x 2 y
- параллельные прямые:
Линии уровня: x 2 y c
при c 1 - прямая x 2 y 1;
при c 2 - прямая x 2 y 2 и т.д.
4
5.
Пример 3. z x 2 y 2Линии уровня: x 2 y 2 c
при c 0 - окружности радиуса c ;
значение c 0 функция принимает
только в одной точке – начале координат.
Пример 4. z xy
Линии уровня:
xy c
при c 0 - гиперболы xy c 2 ,
при c 0 оси координат x 0 и y 0 .
Линии уровня помогают без построения трехмерного
чертежа понять, как выглядит поверхность z = f(x; y).
Примеры линий уровня можно увидеть на
географических картах, где изображены линии, на
которых высота точек земной поверхности над уровнем
моря постоянна.
5
6.
Аналогично для функций трех переменных вводится понятие поверхностиуровня.
Опр. 3. Поверхностью уровня функции трех переменных
u f ( x; y; z ) называется множество точек пространства, в
которых функция принимает одно и то же значение c, т. е.
f ( x; y; z ) c.
6
7.
§ 2. Предел и непрерывность Ф2ПОпр. 1. -окрестностью O ( M 0 ) точки M 0 ( x0 ; y0 ) называется
O ( M 0 ) M ( x; y) :| M 0 M | ( x x0 ) 2 ( y y0 )2 .
M0(x0; y0)
Другими словами, -окрестность O ( M 0 ) точки M 0 – это все
внутренние точки круга с центром M 0 и радиусом .
Опр. 2. Проколотой -окрестностью O ( M 0 ) точки M 0
называется -окрестность точки M 0 без самой этой точки.
8.
Пусть функция z f ( x; y ) определена в некоторой окрестноститочки M 0 ( x0 ; y0 ), быть может, без самой этой точки.
Опр. 3. Число A называется пределом функции z f ( x; y ) при
x x0 , y y0 (или в точке ( x0 ; y0 ) ): lim f ( x; y ) A, если для
x x0
y y0
любой сколь угодно малой -окрестности O ( A) точки A найдется
такая проколотая -окрестность O ( M 0 ) точки M 0 ( x0 ; y0 ), что
для всех точек ( x; y ) O ( M 0 ) имеет место f ( x; y ) O ( A).
Сформулируем также определение предела «на языке последовательностей».
8
9.
Рассмотримпоследовательность
M1 ( x1; y1 ), M 2 ( x2 ; y2 ), ..., M n ( xn ; yn ), ....
Опр. 4. Говорят, что последовательность
M1 ( x1; y1 ), M 2 ( x2 ; y2 ), ..., M n ( xn ; yn ), ...
сходится
к
M 0 ( x0 ; y0 ), если
точек:
точек
точке
lim | M 0 M n | lim ( xn x0 )2 ( yn y0 )2 0.
n
n
Опр. 5. Число A называется пределом функции z f ( x; y ) в
точке M 0 ( x0 ; y0 ) : lim f ( x; y ) A, если для любой сходящейся к
x x0
y y0
M 0 ( x0 ; y0 ) последовательности точек
M1 ( x1; y1 ), M 2 ( x2 ; y2 ), ..., M n ( xn ; yn ), ..., отличных от M 0 ( x0 ; y0 ),
соответствующая последовательность значений функции
f ( x1; y1 ), f ( x2 ; y2 ), ..., f ( xn ; yn ), ... сходится к числу A.
Утв. 1. Определение 3 и определение 5 эквивалентны.
9
10.
Утв. 1. Определение 3 и определение 5 эквивалентны.Основные теоремы о пределах (основные свойства пределов),
сформулированные для функций одной переменной, переносятся
на случай ФНП.
Тем не менее, вычисление пределов Ф2П – задача гораздо более сложная, чем для
функций одной переменной.
10
11.
ln(1 x 2 y 2 )Пример 1. Вычислим lim
.
2
2
x 0
x y
y 0
ln(1 x 2 y 2 ) 0
Решение. lim
2
2
x 0
x y
0
y 0
t x2 y 2
ln(1 t )
x 0
lim
t
0
t
t 0
y 0
ln(1 ) при 0
t
lim 1.
t 0 t
ln(1 t ) t при t 0
11
12.
x2 y 2Пример 2. Рассмотрим предел lim 2
.
2
x 0 x y
y 0
Если сначала определить предел данной функции при x 0, а
затем найти предел при y 0, вычислим повторный предел
x2 y 2
0 y2
limlim 2
lim
1.
2
2
y 0 x 0 x y
y 0 0 y
Другой повторный предел равен
x2 y 2
x2 0
limlim 2
lim 2
1.
2
x 0 y 0 x y
x 0 x 0
֜?
.
Понятие повторного предела отличается от введенного в
определениях 3 и 5 понятия двойного предела, который не зависит
от пути, по которому точка M ( x; y) приближается к M 0 ( x0 ; y0 ).
!
12
13.
x2 y 2Покажем, что двойной предел lim 2
не существует. Для
2
x 0 x y
y 0
этого
используем
определение
предела
на
языке
последовательностей (определение 5).
1 1
1) Рассмотрим последовательность точек M n ; (0; 0).
n n n
2
2
1
1
В этом случае
0
n n
lim f ( M n ) lim
lim
0.
2
2
2
n
n 1
n
1
1
2
n n
n
1
2) Рассмотрим последовательность точек M n ; 0 (0; 0). В
2
n 2 n
1
1
2
этом случае
0
n
n
lim f ( M n ) lim 2
lim 2 1.
n
n
n 1
1
0
n
n
13
14.
Таким образом, для двух разных сходящихся к (0; 0)последовательностей точек соответствующие последовательности
значений функции сходятся к разным числам 0 и 1. Следовательно,
в соответствии с определением 5 предела на языке
x2 y 2
последовательностей, двойной предел lim 2
не существует.
2
x 0 x y
y 0
xy
Упражнение. Показать, что не существует предел lim 2
,
2
x 0 x y
y 0
x2 y
но существует lim 2
.
2
x 0 x y
y 0
14
15.
Опр. 6. Функция z f ( x; y ) называется бесконечно малой приx x0 , y y0 (в точке ( x0 ; y0 ) ), если lim f ( x; y ) 0.
x x0
y y0
Опр. 7. Функция z f ( x; y ) называется непрерывной в точке
( x0 ; y0 ) , если lim f ( x; y ) f ( x0 ; y0 ).
x x0
y y0
Опр. 8. Если функция z f ( x; y ) определена в некоторой
окрестности точки ( x0 ; y0 ) (возможно, проколотой), но условие
непрерывности lim f ( x; y ) f ( x0 ; y0 ) не выполняется, то точка
x x0
y y0
( x0 ; y0 ) называется точкой разрыва функции z f ( x; y ).
В отличие от функций одной переменной, для Ф2П точки
разрыва могут быть изолированными, а могут образовывать линии
разрыва.
15
16.
x2 y 2Пример 3. 1) Функция z 2
имеет точку разрыва (0; 0).
2
x y
1
2) Для функции z
прямая y x является линией
x y
разрыва.
Для функций трех переменных могут возникать также
поверхности разрыва.
Пример
4. Для
функции
u
1
x2 y 2 z 2 9
сфера
x 2 y 2 z 2 9 является поверхностью разрыва.
16
17.
§ 3. Частные производные идифференцируемость функций
нескольких переменных
Пусть функция z f ( x; y ) определена и непрерывна в
некоторой окрестности точки M 0 ( x0 ; y0 ) (включая саму эту точку).
Поскольку x и y – независимые переменные, то они могут
изменяться или оставаться неизменными независимо друг от друга.
Давая некоторое приращение одной из переменных при сохранении
значения другой, получим частное приращение функции.
17
18.
Дадим переменной x в точке M0 приращение Δx, апеременную y оставим без изменения.
Опр. 1. Частное приращение функции z f ( x; y ) по
переменной x в точке M 0 ( x0 ; y0 ), отвечающее приращению
аргумента x, определяется равенством
x z f ( x0 x; y0 ) f ( x0 ; y0 ).
Частное приращение функции z f ( x; y ) по переменной y в
точке M 0 ( x0 ; y0 ), отвечающее приращению аргумента y,
определяется равенством
y z f ( x0 ; y0 y) f ( x0 ; y0 ).
Опр. 2. Полным приращением функции z f ( x; y ) в точке
M 0 ( x0 ; y0 ), отвечающим приращениям аргументов x и y,
называется
z f ( x x; y y ) f ( x ; y ).
0
0
0
0
18
19.
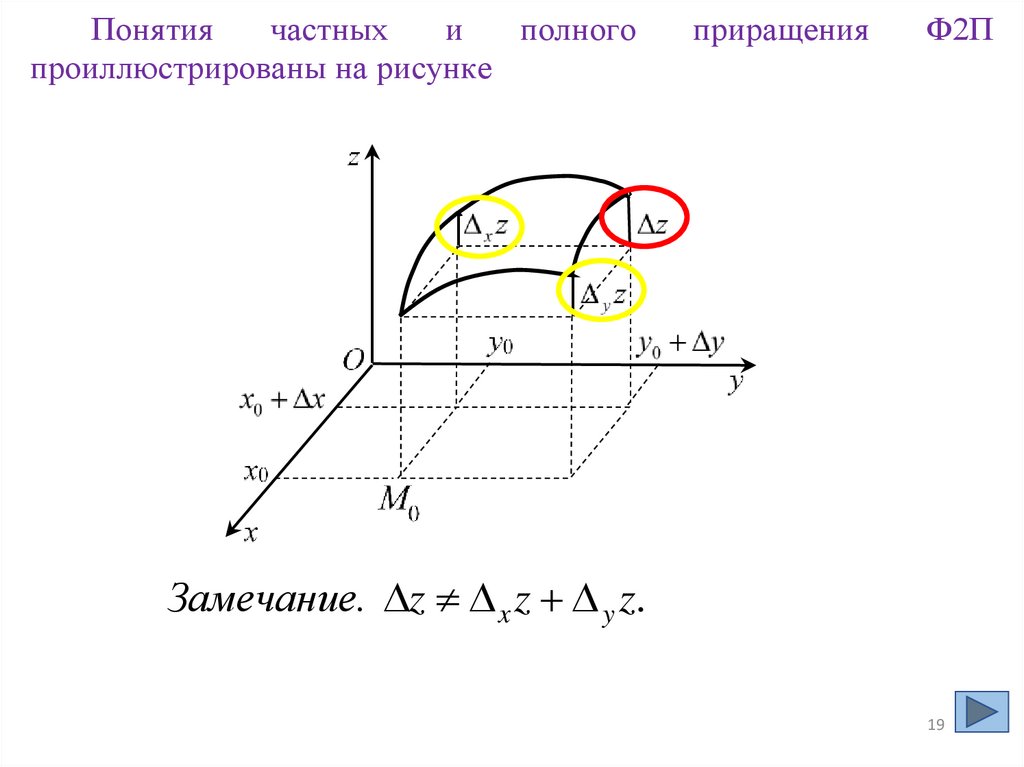
Понятиячастных
и
полного
проиллюстрированы на рисунке
приращения
Ф2П
Замечание. z x z y z.
19
20.
Опр. 3. Частной производной функции z f ( x; y ) понекоторой переменной называется предел (если он существует и
конечен) отношения частного приращения функции по этой
переменной к приращению этой переменной, когда последнее
стремится к 0:
x z
f ( x0 x; y0 ) f ( x0 ; y0 )
lim
;
x 0 x
x 0
x
yz
f ( x0 ; y0 y ) f ( x0 ; y0 )
z y lim
lim
.
y 0 y
y 0
y
z x lim
Частную производную функции z f ( x; y ) по переменной x
z f
обозначают z x , f x , , . Аналогично, частная производная по y
x x
z f
обозначается z y , f y , , .
y y
20
21.
Заметим, что частная производная по х от функциивычисляется в предположении, что у - постоянная величина, а
частная производная по у от функции z вычисляется в
предположении, что х - постоянная.
Следовательно, правила вычисления частных производных
совпадают с правилами вычисления производной для функции
одного переменного и только требуется каждый раз помнить по какому переменному ищется производная.
21
22.
Из определения частной производной следует, что длянахождения
частной
производной
z
по
x
следует
продифференцировать функцию z по переменной x, считая y
постоянным.
Пример 1. Найдем частные производные функции
z x 2 sin( x y 2 ).
Решение. Продифференцируем функцию z по x, считая y
постоянным:
z
2
2
2
2
x
cos
x
y
x sin x y
x y const
x
Дифференцируя по y при фиксированном x, получим
z
x 2 sin x y 2 2 y cos x y 2
y x const
y
22
23.
Примеры.z 2 x 2 y 3xy 2 x 3
z
z x
2 x 2 y 3xy 2 x 3 x 4xy 3y 2 3x 2
x
z
2
2
2
(2
x
y
3
xy
x
)'
2x
6xy
zy
y
у
z x
y
z
y
const
u
y x y 1
x
z
x const a u x y ln x
y
23
24.
xz 2 ln( x 2 y )
y
x
x
2
2
z
ln(
x
y
)
ln(
x
y
)
y
const
y2
2
x
y
x
x
1
x
2x
2
2 ln( x y )
2
2
y
y x y
z x
x
2
2
ln(
x
y
)
ln(
x
y
)
2
2
y
y
y
y
y
x
1
2x
2
3 ln( x y ) 2 2
y x y
y
24
25.
Аналогично физическому смыслу производной функцииодной переменной, частная производная ФНП характеризует
скорость
изменения
функции
при
изменении
соответствующей переменной.
Физический смысл частной производной.
z
Частная производная
x
характеризует скорость изменения
функции в точке M в направлении оси
Ox.
25
26.
Геометрический смысл частных производныхГрафик функции z=f (x,y) представляет некоторую поверхность.
Фиксируя на поверхности z f ( x; y ) одну из переменных, например,
y y0 , получаем некоторую линию – сечение поверхности плоскостью y y0 .
Геометрический смысл частных производных: значение
частной производной функции z f ( x; y ) по переменной x в точке
M 0 ( x0 ; y0 ) равно тангенсу угла наклона касательной, проведенной
в точке K 0 ( x0 ; y0 ; f ( x0 ; y0 )) к линии пересечения поверхности
z f ( x; y ) и плоскости y y0 :
z
( x0 ; y0 ) tg .
x
Аналогично:
z
( x0 ; y0 ) tg
y
Здесь α и β - углы, образованные касательными с
плоскостью ОХУ, проходящими через точку K0 параллельно26
плоскостям ОХZ и ОУZ соответственно.
!
27.
Дифференцируемость функции двух переменныхПусть функция z=f(x,y) определена в некоторой
окрестности точки M, тогда полное приращение этой
функции в точке М имеет вид:
z f ( x x, y y ) f ( x, y )
Опр. 4. Функция z f ( x; y ) называется дифференцируемой в
точке ( x0 ; y0 ), если ее полное приращение в этой точке
представимо в виде
z A x B y ( x; y) x ( x; y) y,
где A и B – некоторые числа, зависящие только от точки ( x0 ; y0 ), но
не зависящие от x и y, а ( x; y) и ( x; y) –
бесконечно малые при x 0, y 0.
27
28.
Т 1 [необходимое условие дифференцируемости]. Еслифункция z f ( x; y ) дифференцируема в точке ( x0 ; y0 ), то она
непрерывна в этой точке.
Замечание. Обратное, вообще говоря, неверно.
Т 2 [необходимое условие дифференцируемости]. Если
функция z f ( x; y ) дифференцируема в точке ( x0 ; y0 ), то в этой
точке существуют частные производные, причем
z
( x0 ; y0 ) A,
x
z
( x0 ; y0 ) B.
y
28
29.
Доказательство.Так как функция дифференцируема в точке М, то
z A x B y x y
Положим y 0 x 0
x z
A
Получим x z A x x Отсюда находим
x
Переходя к пределу при х 0, получим
x z
z
lim
A
x
0
x
x
z
Таким образом, в точке M существует частная производная А
x
Аналогично доказывается, что в точке M существует частная
производная z
В
Доказано.
у
Замечание. Обратное утверждение не верно, т.е. из
непрерывности функции или из существования частных
производных не следует дифференцируемость функции.
29
30.
Пример 3. Рассмотрим функцию0 на осях координат,
f ( x; y )
1 в остальных точках плоскости.
Найдем ее частные производные в точке (0; 0) :
f ( x; 0) f (0; 0)
0 0
f x (0; 0) lim
lim
0;
x 0
x 0 x
x
f (0; y) f (0; 0)
0 0
f y (0; 0) lim
lim
0.
y 0
y 0 y
y
Однако функция f ( x; y) не является непрерывной в точке
(0; 0), а следовательно, не является дифференцируемой в этой
точке.
30
31.
Т 3 [достаточное условие дифференцируемости]. Еслифункция z f ( x; y ) в некоторой окрестности точки ( x0 ; y0 ) имеет
частные производные, и эти частные производные непрерывны в
самой точке ( x0 ; y0 ), то функция z f ( x; y ) дифференцируема в
точке ( x0 ; y0 ).
Доказательство.
По определению полного приращения функции z=f(x,y) имеем
z f ( x x, y y ) f ( x, y )
Запишем полное приращение в виде
z f ( x x, y y ) f x, y y f x, y y f ( x, y )
и, учитывая, что функция имеет непрерывные частные
производные, применим теорему Лагранжа, получим
z f x ( x1 , y y ) x f y ( x, y1 ) y
x x1 x x
y y1 y y
31
32.
Так как частные производные непрерывны, то при х 0у 0 получим
lim f y x, y1 f y x, y
lim f x x1 , y y f x x, y
x 0
y 0
x 0
y 0
так как при х 0; и у 0
х1 х и у1 у.
и
Учитывая свойство пределов, запишем
f x x1 ; y y f x x; y x, y
f y x; y1 f y x; y x, y
x, y x, y стремятся к нулю, когда х и у стремятся к нулю.
Имеем
z f x ( x, y ) x f y ( x, y ) y x, y x x, y y
Сумма двух последних слагаемых правой части является
бесконечно малой величиной высшего порядка малости
32
относительно х и у.
Доказано.
33.
Приращения независимых переменных х иу будем
называть дифференциалами независимых переменных х и у и
обозначать соответственно через dx, dy.
Дифференциал функции двух
переменных
Напомним, что функция z f ( x; y ) дифференцируема в точке
( x0 ; y0 ), если ее полное приращение в этой точке представимо в
виде
z
z
z
x
x
y
y ( x; y) x ( x; y) y,
где lim ( x; y) lim ( x; y) 0.
x 0
y 0
x 0
y 0
33
34.
Опр. 5. Если функция z f ( x; y ) дифференцируема в точке( x0 ; y0 ), то главная, линейная относительно x и y часть полного
приращения функции называется полным дифференциалом этой
функции:
z
z
dz
x
x
y
y.
Замечание. Для дифференцируемой функции
достаточно малых значениях x и y.
z dz при
Так как для независимых переменных x dx, y dy, то
z
z
dz dx dy.
x
y
Опр.
6.
Выражения
dx z
z
z
dx, d y z dy
x
y
называются
частными дифференциалами.
Замечание. dz d x z d y z, но z x z y z.
34
35.
Пусть дана дифференцируемая функция z=f(x,y)Тогда её полное приращение
z A x B y x y
где α,β - бесконечно малые функции при Δx 0 Δy 0.
Поэтому при малых x
y
слагаемыми αΔx+βΔy можно пренебречь,
Так как
z f x x, y x f y x, y y
z f x0 x, y0 y f x0 , y0
то из последней формулы имеем
f x0 x, y0 y f x0 , y0 f x x0 , y0 x f y x0 , y0 y
Формула означает линеаризацию функции z=f(x,y)
в
окрестности точки M0 т. е. в этой окрестности произвольную
35
функцию заменяем ее линейным приближением.
36.
Пример.Найти полное приращение и полный дифференциал функции
z = xy в точке(2; 3) при ∆x = 0,1, ∆у = 0,2.
Решение.
Полное приращение
∆ z = (х + ∆x)(y + ∆у) – xy = у∆x + +x∆у + ∆x∙∆у,
∆ z = 3∙0,1 + 2∙0,2 + 0,1∙0,2 = 0,72
Следовательно,
dz
z
z
dx dy = уdx + xdу = у∆x + x∆у.
x
y
dz = 3∙0,1 + 2∙0,2 = 0,7.
36
37.
Пример.Вычислить приближённо 1,053,98.
Решение.
Рассмотрим функцию f x, y x y
и применим формулу линеаризации при
x0 1; x 0, 05
y0 4; y 0, 02.
f x0 x, y0 y f x0 , y0 f x x0 , y0 x f y x0 , y0 y
f 1, 4 14 1 f x y x y 1 1,4 4 f y x y ln x 1,4 0
Таким образом, 1,053,98 ≈1 + 0,2 = 1,2.∙
37
38.
Геометрический смыслдифференциала
С геометрической точки зрения, производная функции одной
переменной равна тангенсу угла наклона касательной, а
дифференциал – приращению ординаты касательной,
проведенной к графику функции в данной точке.
Частная производная Ф2П геометрически равна тангенсу угла
наклона касательной к линии, которая получается в сечении
z f ( x; y )
поверхности
соответствующей
вертикальной
плоскостью.
Если к поверхности z f ( x; y ) провести в точке ( x0 ; y0 ; z0 ), где
z0 f ( x0 ; y0 ), касательную плоскость, то эта плоскость будет
содержать все касательные к кривым, проведенным на поверхности
через эту точку. Уравнение касательной плоскости к поверхности
z f ( x; y ) в точке M 0 ( x0 ; y0 ) имеет вид
z z0 f x ( x0 ; y0 )( x x0 ) f y ( x0 ; y0 )( y y0 ).
38
39.
Геометрический смысл дифференциала: дифференциалфункции z f ( x; y ) в точке ( x0 ; y0 ), отвечающий приращениям
аргументов x и y, равен приращению аппликаты касательной
плоскости, проведенной к поверхности в этой точке.
39
40.
Частные производные высших порядковz
z
Частные производные
и
называют частными
x
y
производными первого порядка. Так как частные производные
первого порядка являются функциями двух переменных, то они
также могут иметь частные производные, которые называются
частными производными второго порядка:
z 2 z
2 z xx f xx x, y
x x x
z 2 z
z xy f xy x, y
y x x y
z 2 z
z yx f yx x, y
x y y x
z 2 z
2 z yy f yy x, y
y y y
2 z
2 z
Производные
и
называются смешанными частными производными.
40
x y y x
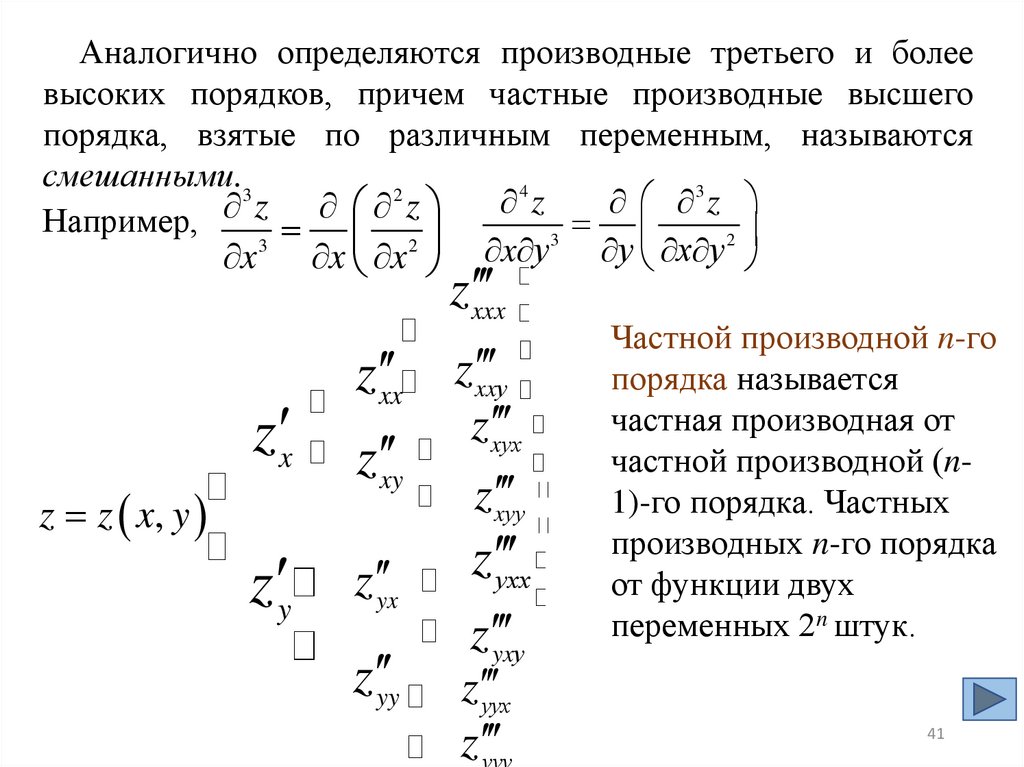
41.
Аналогично определяются производные третьего и болеевысоких порядков, причем частные производные высшего
порядка, взятые по различным переменным, называются
смешанными.3
4
3
2
z
z
Например, z z
3
2
3
2
x
у
у
x
у
x x x
z xxx
z x
z z x, y
z y
z xx z xxу
z xy
z yx
z yy
z xуx
z xуy
z уxx
z yxу
z уyx
z уyy
Частной производной n-го
порядка называется
частная производная от
частной производной (n1)-го порядка. Частных
производных n-го порядка
от функции двух
переменных 2n штук.
41
42.
Пример 4. Найдем все частные производные 2-го порядка дляфункции z x 2 sin( x y 2 ).
2
2x
cos
x
y
zx
2
2
sin
x
y
z
z xx x x
z z sin x y 2 2 y
xy
z y cos x y 2 y
2
x
y
z yy cos x y 2 y y
2
2
2
y
sin
x
y
2 cos x y
2y
2
2cos x y 2 4 y 2 sin x y 2
z yx sin x y
2
2y
42
43.
Пример 5. Найдем все частные производные 2-го порядка дляфункции z x y .
z
y 1
Решение. Поскольку
yx ,
x
2 z
y 2
y 1
y
(
y
1)
x
;
yx
2
x
x
2 z
yx y 1
y
y x
x y 1 yx y 1 ln x.
Поскольку
2 z
x y ln x
x
x y
z
x y ln x,
y
yx y 1 ln x x y 1;
2 z
y
x y ln 2 x.
x
ln
x
y
y 2
2z
2 z
.
Заметим, что в обоих примерах
y x x y
43
44.
Т 4. Если частные производные высшего порядка непрерывны,то смешанные производные одного порядка, отличающиеся только
порядком дифференцирования по различным переменным, равны
2z
2z
, или z yx z xy .
между собой, в частности:
x y y x
3 z
, если z cos xy.
Пример 6. Найдем
2
x y
Решение. Найдем последовательно:
z
sin xy ( xy ) x y sin xy;
x
2 z
y sin xy y sin xy xy cos xy;
y x
3 z
2 x cos xy x 2 y sin xy.
sin
xy
xy
cos
xy
y
x y 2
44
45.
Пример. Найти частные производные высших порядков.u x y ( z 1)
3
5
7
u
3 x 2 y 5 ( z 1) 7
x
3u
?
x y z
2u
2 4
7
15 x y ( z 1)
x y
3u
105 x 2 y 4 ( z 1)6
x y z
3
3
z
z
3 2
3
5
z x y 5 xy x 1 x 2 y , y 2 x ?
z
3x 2 y 2 5y 3 5x 4
x
z
3
2
2 x y 15 xy
y
3
z
2 z
2
3
12xy
6xy 20x
2
2
x y
x
2 z
3
2
x
30 xy
2
y
3 z
2
6
x
30 y
2
y x
45
46.
Дифференциалы высших порядковПолный
дифференциал
ФНП
дифференциалом первого порядка.
называют
также
Опр. 7. Дифференциалом второго порядка называется
дифференциал от дифференциала первого порядка: d 2 z d (dz ).
Аналогично, дифференциалом n-го порядка называется
дифференциал
от
дифференциала
порядка:
(n 1) -го
d n z d (d n 1z ).
Пусть функция z f ( x; y ) имеет непрерывные частные
производные, x и y – независимые переменные (заметим, что dx и
dy не зависят от изменения x и y). Вычислим дифференциал второго
порядка
46
47.
zz
d z d (dz ) d dx dy
y
x
z
z
z
z
dx dy dx dx dy dy
y x
y y
x
x
2
2 z
2 z
2 z
2 z
2 dx
dy dx
dx 2 dy dy
x y
y
x
y x
z 2
z
z 2
2 dx 2
dxdy 2 dy .
x y
x
y
2
2
2
47
48.
Заметим, что выражение для d2z похоже на квадрат двучлена.Назовем оператором правило, посредством которого каждой
функции из заданного множества функций, ставится в
соответствие некоторая функция из, вообще говоря, другого
множества (одна функция преобразуется в другую функцию).
Оператор d dx dy назовем оператором дифференциала.
x
y
При действии этого оператора на функцию z=f(x,y)
получается дифференциал функции:
z
z
dz dx dy
x
y
Произведение операторов определим следующим образом:
2
x y x y
2
2
x x x x
2
48
49.
Тогда второй дифференциал можно записать в виде2
2
d z dx dy z
y
x
Дифференциал от дифференциала (п-1)-го порядка
называется дифференциалом п-го порядка функции
z=f(x,y)
d n z d d n 1 z
n
dx dy z.
Символически можно записать, что d z
y
x
n
Можно показать, что так же, как в случае функций одной
переменной, дифференциал первого порядка ФНП обладает
свойством инвариантности формы (т. е. форма записи
дифференциала первого порядка не зависит от того, являются ли
х и у независимыми переменными или функциями других
переменных), а дифференциалы 2-го и более высоких порядков
не обладают этим свойством.
49
50.
§ 4.Дифференцирование
сложных
неявных
функций
§ 4.
Дифференцирование
сложных
ии
неявных
функций
нескольких
переменных
нескольких
переменных
Правило дифференцирования сложной функции
1. Случай одной независимой переменной. Пусть
z z ( x; y ) – дифференцируемая функция двух переменных х и у,
которые, в свою очередь, являются дифференцируемыми
функциями переменной t: х = х(t), у = y(t). В этом случае функция
z z ( x(t ); y(t )) является сложной функцией одной независимой
переменной t, переменные х и у называются промежуточными
аргументами.
Т 1. Если функции x(t ) и y (t ) дифференцируемы в точке t0 , а
функция z z ( x; y ) дифференцируема в точке ( x0 ; y0 ), где
x0 x(t0 ), y0 y (t0 ), то сложная функция z z ( x(t ); y(t ))
дифференцируема в точке t0 , причем
dz z dx z dy
.
(1)
dt x dt y dt
50
51.
Доказательство. Чтобы доказать, что функция z z ( x(t ); y(t ))дифференцируема в точке t0 , нужно показать, что существует
dz
z
lim .
dt t 0 t
Дадим независимой переменной t приращение ∆t. Тогда
переменные х и у получат приращения ∆х и ∆у, а функция z –
приращение ∆z соответственно. Так как функция z z ( x; y )
дифференцируема, то
z
z
z x y ( x; y) x ( x; y) y,
x
y
где lim ( x; y) lim ( x; y) 0.
x 0
y 0
x 0
y 0
Если t 0, то в силу того, что функции х = х(t) и у = y(t)
дифференцируемы, а следовательно, непрерывны, x 0, y 0.
51
52.
Поэтому, переходя в равенствеz z x z y
x
y
( x; y)
( x; y)
t x t y t
t
t
к пределу при t 0, получим
dz
z z dx z dy
dx
dy z dx z dy
lim
0 0
.
t
0
dt
t x dt y dt
dt
dt x dt y dt
Следствие 1. Если z z ( x; y ) – дифференцируемая функция
двух переменных х и у, причем х – независимая переменная, а
y y ( x) – дифференцируемая функция, то
dz z z dy
.
dx x y dx
(2)
dz
Замечание. В этом случае производную
называют полной
dx
z
производной z по x в отличие от частной производной .
x
52
53.
Пример 1. Найдем производнуюdz
, если
dt
2
1
z
1 tg 2 t tg 4 t e cos t .
cos t
1
Решение. Обозначим x tg t , y
cos t
2
dz z dx z dy
.
dt x dt y dt
и воспользуемся формулой
Найдем частные производные функции
(1)
z y 1 x x 2 e2 y :
z
1 2x
2
2y
y
;
y 1 x x e
2
x
x
2 1 x x
z
2
2y
y 1 x x e
1 x x 2 2e 2 y .
y
y
53
54.
Учитывая, что2tg t 2sin t
dx
2
;
(tg t )
2
3
cos t cos t
dt
dy 1
sin t
,
2
dt cost
cos t
по формуле (1) получим полную производную
dz z dx z dy
1 2x
2sin t
2
2 y sin t
y
(
1
x
x
2e
) 2 .
2 cos3 t
cos t
2 1 x x
dt x dt y dt
Подставим в получившееся выражение
x tg 2 t , y
1
,
cos t
получим окончательный ответ:
2
sin t
dz
1 2tg 2 t
sin t
2
4
cos t
1 tg t tg t 2e 2 .
2
4 cos 4 t
1 tg t tg t
cos t
dt
54
55.
Пример2. Найдем
полную
z 4 x 2 y 5 , y arcsin x3.
Решение. Используем формулу (2).
Найдем
z
5
4 x 2 y 5 8 xy ;
x
x
z
2 4
4 x 2 y 5 20 x y ;
y
y
3x 2
dy
3
.
arcsin x
6
dx
1 x
производную
dz
,
dx
если
dz z z dy
.
dx x y dx
Тогда в силу (2) полная производная равна
dz z z dy
3x 2
60 x 4 y 4
5
2 4
5
8 xy
8 xy 20 x y
.
6
6
dx x y dx
1 x
1 x
Подставляя y arcsin x3 , получим
4
4 3
dz
60
x
arcsin
x
8x arcsin 5 x3
.
6
dx
1 x
55
56.
2. Случай нескольких независимых переменных.Следствие 2. Если z z ( x; y ) – дифференцируемая функция
двух
переменных
х
и
у,
а
x x(u; v), y y(u; v) –
дифференцируемые функции двух независимых переменных u и v,
то
z z x z y z z x z y
;
.
(3)
u x u y u v x v y v
Формулы (1), (2), (3) и аналогичные им записываются в соответствии со
следующим правилом.
Правило дифференцирования сложной ФНП: производная
сложной функции по независимой переменной равна сумме
произведений частных производных по промежуточным
аргументам на производные этих аргументов по независимой
переменной.
56
57.
Пример 3. Найдем частные производные сложной функцииz u ln v, где u 3x y, v x 2 y 2 .
Решение. Поскольку z z (u; v); u u( x; y); v v( x; y),
то по правилу дифференцирования сложной функции запишем формулы для
частных производных функции z по независимым переменным x и y:
z z u z v z z u z v
;
.
x u x v x y u y v y
Вычислим вспомогательные производные:
z
u ln v u ln v;
u
u
3x y x 3;
x
u
3x y y 1;
y
Следовательно,
u
z
u ln v v ;
v
v
v
x 2 y 2 2 x;
x
x
v
x 2 y 2 2 y.
y
y
z
u z
u
3ln v 2 x ;
ln v 2 y ,
x
v y
v
2 y (3x y )
2 x(3x y ) z
z
2
2
.
)
y
x
(
ln
;
3ln( x 2 y 2 ) 2
2
2
2
y
x
x y
x y
или
57
58.
Дифференциал сложной функции.Если z=f(x,y)– дифференцируемая функция двух независимых
z
z
переменных, то
dz dx dy
x
y
Преимущество формулы в том, что она остается верна и в
том случае, когда z=f(x,y) – сложная функция.
Пусть z=f(x,y), где x=φ1(u,v), y=φ2(u,v). Предположим, что
функции f (x,y) , φ1(u,v) , φ2(u,v) дифференцируемы.
Тогда сложная функция z=f (φ1(u,v), φ2(u,v)) тоже будет
дифференцируема и ее полный дифференциал по формуле
будет равен
z
z
dz
u
du
v
dv
Применяя формулу для вычисления частных производных
сложной функции, получаем
58
59.
z x z yz x z y
dz du dv
x u y u
x v y v
z x
x z y
y
du dv du dv
x u dx v y u dy v
Так как в скобках стоят полные дифференциалы
функций x=φ1(u,v) и y=φ2(u,v), то окончательно имеем
z
z
dz dx dy
x
y
Итак, как и в том случае, когда x и y – независимые
переменные, так и когда x и y – зависимые переменные,
дифференциал функции z=f(x,y) можно записать в виде
z
z
dz dx dy
x
y
В связи с этим, данная форма записи
дифференциала называется инвариантной.
полного
59
60.
Если аргументы x и y функции u(x, y) не являютсянезависимыми
переменными,
а
являются
дифференцируемыми функциями каких-то независимых
переменных t1,t2,…,tn , то формула
2
d z dx dy z
y
x
2
изменится.
В силу инвариантности формы 1-го дифференциала имеем:
u
u
du
dx dy
x
y
где dx и dy являются функциями t1,t2,…,tn , dt1,dt2,…,dtn , а
u
функциями t1,t2,…,tn .
y
u
x
При вычислении второго дифференциала d2u, как
дифференциала от первого дифференциала, рассматриваем du
как функцию t1,t2,…,tn , то есть учитываем зависимость от
t1,t2,…,tn всех входящих в du слагаемых и сомножителей: 60
61.
uu
u
u
u
u
d 2u d dx dy d dx d 2 x d dy d 2 y
y
x
y
x
x
y
2
u 2
u
dx dy u d x d 2 y
y x
y
x
Мы видим, что по сравнению со случаем, когда x и y —
независимые переменные, выражение для d2u содержит
дополнительные слагаемые (они заключены в фигурные
скобки).
Таким образом, форма второго дифференциала не
инвариантна. То же самое относится к дифференциалам
более высокого порядка.
61
62.
Производная неявной функцииРассмотрим уравнение с двумя переменными F(x;y)=0.
Пусть уравнение F(x;y)=0 имеет решение y=f(x). Данное
решение и называется неявной функцией.
Пример.
В прямоугольнике Q={xє[-1;1],y є[0;1]} рассмотрим уравнение
F(x;y)=x2+y2-1=0.
Решая, получим, что ∀ xє[-1;1] y 1 x 2
Это неявная функция, определяемая уравнением F(x;y)=x2+y2-1=0.
Пример.
Рассмотрим уравнение F(x;y)=2y+siny-x=0
Уравнение имеет единственное решение y=f(x), но найти его в
явном виде не удастся.
Не всякое уравнение F(x;y)=0 определяет неявную функцию. И
если оно определяет неявную функцию, то мы различаем два
момента: существование неявной функции и возможность найти
62
ее в явном виде.
63.
ТеоремаПусть выполнены условия:
1) функция F(x;y) определена и непрерывна в прямоугольнике
Q={(x;y): a x b, c y d}
2) ∀ x, a x b: F(x;c) F(x;d)<0, то есть на верхней и нижней
сторонах прямоугольника Q функция F(x;y) имеет разные знаки
3)∀ x, a x b: F(x;y) является строго монотонной функцией
переменной c y d.
Тогда:
1) в прямоугольнике Q уравнение F(x;y)=0 имеет единственное
решение относительно y (y=f(x), причем c f(x) d, т.е. в
прямоугольнике Q уравнение F(x;y)=0 определяет неявную
функцию вида y=f(x);
2) y =f(x) непрерывна на интервале a x b.
63
64.
Т 2. Пусть функция z z ( x; y ) задана неявно уравнениемF ( x; y; z ) 0 и функция F ( x; y; z ) имеет непрерывные частные
производные по всем аргументам, причем Fz ( x; y; z ) 0. Тогда
z
F
x;
x
Fz
Fy
z
.
y
Fz
Доказательство.
Используя правило дифференцирования сложной функции,
продифференцируем уравнение F ( x; y; z ) 0 по переменной х,
помня, что х и у – независимые переменные, а z z ( x; y ) – функция:
F
F
F z
1
0
0
x
y
z x
z
F
x
x
F
.
z
z
F
y
y
F
.
z
Аналогично, дифференцируя по у, получим
F
F
F z
0
1
0
x
y
z y
64
65.
Пример 4. Найдем частные производные функции z z ( x; y ),заданной уравнением z e xy e z x.
Решение. Обозначим F ( x; y; z ) e xy e z x z и найдем
частные производные этой функции:
xy
xy
z
y
e
1;
Fx e e x z
x
xy
z
Fy e e x z x e xy ;
y
xy
z
Fz e e x z e z 1.
Тогда
z
z
Fx
y e xy 1
z
;
x
Fz
e 1
Fy
z
x e xy
z .
y
Fz
e 1
65
66.
Замечание. Производную функции одной переменной y y( x),заданной неявно уравнением F ( x; y) 0, можно найти по
аналогичной формуле
dy
Fx
.
dx
Fy
dy
x2 y 2
, если 2 2 1.
Пример 5. Найдем
dx
a b
Решение.
Обозначим
x2 y 2
и
найдем
частные
F ( x; y) 2 2 1
a
b
производные этой функции:
2
2
2
2
2y
x
y
x
2x
y
.
Fy 2 2 1
Fx 2 2 1 2 ;
2
b
a b
y
a b
x a
Следовательно,
2 x b2
b2 x
dy
Fx
2
2 .
dx
Fy
a 2y
a y
66
67.
Рассмотрим уравнение F(x1,x2,…,xn,y)=0.Решение этого уравнения относительно y является функцией n
переменных y=f(x1,x2,…,xn) и называется неявной функцией,
определяемой уравнением F(x1,x2,…,xn,y)=0.
Теорема
Пусть выполнены условия:
1) функция F(x1,x2,…,xn,y) определена и дифференцируема в
некоторой окрестности точки M0(x10,x20,…,xn0 ,y0);
2) частная производная F'y (x1,x2,…,xn,y) непрерывна в точке M0
3) F(M0)=0, F’y (M0) ≠ 0
Тогда:
существует параллелепипед Q={(x1,x2,…,xn,y): │xi-xi0│<di
i=1,…,n │y-y0│ c di 0 c 0}, в котором уравнение
F(x1,x2,…,xn,y)=0 определяет единственную неявную функцию
вида y=f(x1,x2,…,xn). Эта функция дифференцируема, и ее
частные производные выражаются формулой:
Fx x1 , x2 ,..., xn , y
f
xi
Fy x1 , x2 ,..., xn , y y f x , x ,..., x
67
1 2
n
68.
Касательная плоскость и нормаль к поверхности.Рассмотрим одно из геометрических приложений частных
производных функций двух переменных. Напомним, что
для функции одной переменной y y=f(x) из
дифференцируемости в точке x0 следует существование
касательной к графику функции в точке (x0,f(x0)).
Рассмотрим функцию
двух
переменных
z=f(x,y), (x;y)єD
Ее
графиком
является
поверхность
S={N(x,y,f(x,y)),(x,y)єD} в
прямоугольной системе
координат
68
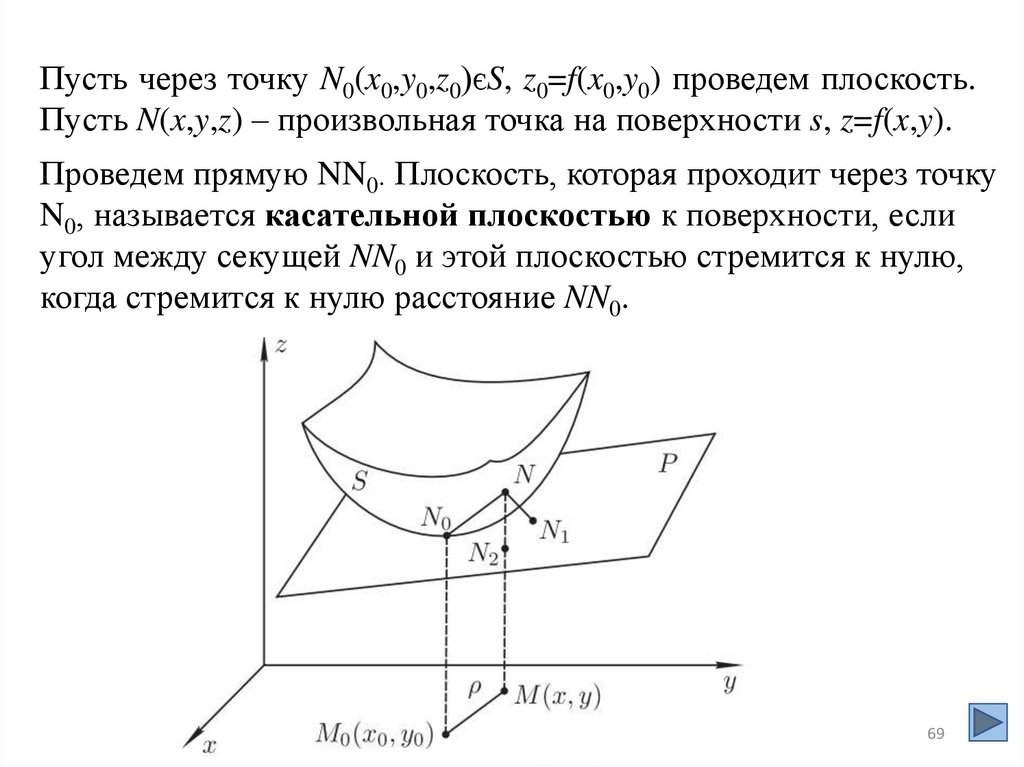
69.
Пусть через точку N0(x0,y0,z0)єS, z0=f(x0,y0) проведем плоскость.Пусть N(x,y,z) – произвольная точка на поверхности s, z=f(x,y).
Проведем прямую NN0. Плоскость, которая проходит через точку
N0, называется касательной плоскостью к поверхности, если
угол между секущей NN0 и этой плоскостью стремится к нулю,
когда стремится к нулю расстояние NN0.
69
70.
Теорема.Если функция z=f(x,y)дифференцируема в точке
M0(x0,y0), то в точке N0(x0,y0,z0), где z0=f(x0,y0), существует
касательная плоскость к этой графику функции.
Доказательство.
Так как функция z=f(x,y) дифференцируема в точке, то ее
приращение Δz можно представить в виде
z
z
z M 0 x M 0 y o
x
y
M , M 0 x y
z
z
Введем обозначения:
M 0 A, M 0 B
x
y
и перепишем условие дифференцируемости в виде
2
2
z z0 A x x0 B y y0 o
Рассмотрим плоскость Р, заданную уравнением Z-z0=A(x-x0)+B(y-y0)
и докажем, что она является касательной плоскостью к поверхности
70
S в точке N0(x0,y0,z0).
71.
Плоскость P проходит через точку N0(x0,y0,z0) и имеет векторнормали n A, B, 1 . Нам надо доказать, что
N , N1
0
N , N0
N N0 N S
NN1 P N1 P
Пусть N2 — точка пересечения прямой NM с плоскостью P.
Точка N2 имеет координаты (x,y,Z=z0+A(x-x0)+B(y-y0)), поэтому
N , N0 z Z o .
Так как
ρ(N, N1) ≥ρ(N, N2) (перпендикуляр меньше
наклонной), а ρ(N, N0) ≥ ρ(M, M0) = ρ, то
N , N1 N , N 2 o
0 при N N 0
N , N0 M , M 0
Таким образом, уравнение касательной плоскости
z z0 f x x0 , y0 x x0 f y x0 , y0 y y0
Доказано.
71
72.
zz
Вектор n M 0 , M 0 , 1
y
x
называется вектором нормали к поверхности S в точке N0(x0,y0,z0).
Определение.
Нормалью к поверхности в точке N0 называется прямая,
проходящая через точку N0 перпендикулярно касательной
плоскости к этой поверхности.
Уравнение нормали к поверхности в этой точке:
x x0
y y0
z z0
f x ( x0 y0 ) f y ( x0 , y0 )
1
Если поверхность S задана уравнением F(x,y,z)=0, то уравнения
касательной плоскости и нормали к поверхности примут вид:
Fx N 0 x x0 Fy N 0 y y0 Fz N 0 z z0 0
x x0
y y0
z z0
Fx ( N 0 ) Fy ( N 0 ) Fz ( N 0 )
72
73.
Формулы касательной плоскости и нормали поверхностиполучены для обыкновенных, т.е. не особых, точек
поверхности. Точка M0 поверхности называется особой, если
в этой точке все частные производные равны нулю или хотя
бы одна из них не существует.
Пример. Найти уравнения касательной плоскости и нормали к
поверхности z=x2-2xy+y2-x+2y-1 в точке М(1,1,0)
Решение.
z
z
2 x 2 y 1 M 1;
2 x 2 y 2 M 2
x
y
Уравнение касательной плоскости:
z 0 1 x 1 2 y 1
x 2y z 1 0
Уравнение нормали: x 1
y 1 z
1
2
1
73
74.
Пример.Найти уравнения касательной плоскости и нормали к поверхности
x 3 у 3 z 3 xyz , в точке М(1,1,-1)
Решение.
Fx 3 x 2 yz 3-1=2
M
Fy 3 y 2 xz M 2
Fz 3 z 2 xy
4
2 x 1 2 y 1 4 z 1 0 или x y 2 z 0
M
Уравнение нормали: x 1
y 1 z 1
1
1
2
74
75.
§ 5. Производная по направлению и градиентЧастные производные характеризуют скорость изменения
функции при изменении только одной переменной, т. е. при
движении вдоль координатных осей. Для характеристики скорости
изменения функции в направлении заданного вектора l вводится
понятие производной по направлению.
Пусть функция двух переменных z=f(x;y) определена в
некоторой области D плоскости Oxy, M0(x0;y0) – точка
области D, l –вектор любого направления.
Функция z=f(x;y) получит при этом приращение
z f x0 x, y0 y f x0 , y0
Разделим приращение функции Δz(M0) на длину отрезка
смещения MM0.
z ( M 0 )
Полученное отношение
MM 0
дает среднюю скорость изменения функции z на участке
75
MM0.
76.
Опр. 1. Производной функции z f ( x; y ) в точке M 0 ( x0 ; y0 )по направлению вектора l lx i l y j называется предел, если он
существует и конечен, отношения приращения функции в данном
направлении к величине перемещения при условии, что величина
перемещения стремится к 0:
z
l z
lim
,
l
0
l
l
l M 0 M
!
M ( x0 x, y0 y )
M 0 M l
l z f x0 x, y0 y f x0 , y0
76
77.
Выведем формулу для вычисления этой производной.Направление вектора на плоскости полностью характеризуется
углами и , которые вектор образует с осями координат, причем
если l lx i l y j , то
ly
l
cos
Для точек
x
l x2 l 2y
M 0 ( x0 ; y0 ) и
M 0 M l , получим
l M 0 M ;
; cos
l x2 l 2y
.
M ( x0 x; y0 y ), таких, что
x l cos ;
y l cos .
Так как функция z f ( x; y ) дифференцируема в точке
M 0 ( x0 ; y0 ), то ее полное приращение в этой точке представимо в
виде
z
z
z
x y ( x; y) x ( x; y) y,
x
y
где lim ( x; y) lim ( x; y) 0. Поэтому
x 0
y 0
x 0
y 0
77
78.
zz
l z l cos l cos ( x; y) l cos ( x; y) l cos ;
x
y
l z z
z
cos cos ( x; y) cos ( x; y) cos .
l x
y
Если l 0, то x 0, y 0, поэтому, переходя к пределу
при l 0, получим формулу
z z
z
cos cos .
l x
y
!
78
79.
Аналогично,производная
функции
u u( x; y; z )
трех
переменных по направлению вектора l lx i l y j lz k равна
u u
u
u
cos cos cos ,
l x
y
z
где
cos
lx
l
; cos
ly
l
; cos
lz
–
направляющие
!
косинусы
l
вектора l ; l l x2 l 2y l z2 – длина вектора l .
Очевидно, частные производные являются производными по
направлениям координатных осей.
Скорость изменения функции по направлению l является
линейной комбинацией скоростей изменения этой функции
по направлениям координатных осей, т.е. линейной
комбинацией частных производных u u u
,
,
x y z
79
80.
Причем коэффициентами этой линейной комбинации выступаюткоординаты cos ,cos ,cos единичного вектора l , задающего
направление;
эти
коэффициенты
являются
весовыми
множителями, показывающими, какую долю вносит каждая
частная производная в производную по направлению.
80
81.
Пример 1. Найдем производную функции u xy 2 z 3 в точкеM 0 (1; 2; 1) по направлению вектора l {2; 3; 6}.
Решение. Найдем частные производные и их значения в
точке M0:
u
2
3
u
2 3
2 3
(
2)
(
1)
4;
xy z
y z ;
x M 0
x
x
u
3
u
xy 2 z 3 2 xyz ;
2 1 ( 2) ( 1)3 4;
y
y M
y
0
u
u
2 2
3 1 ( 2)2 ( 1)2 12.
xy 2 z 3 3 xy z ;
z
z M 0
z
Найдем длину и направляющие косинусы вектора l :
l
22 32 ( 6)2 7;
2
3
6
cos ; cos ; cos .
7
7
7
Следовательно, производная по направлению равна u
l
u
u
u
cos cos cos ,
x
y
z
u
2
3
68
6 8 12 72
4 4 12
.
l M 0
7
7
7
7
7
81
82.
Производная по направлению определяет скорость измененияu
( M 0 ) 0, то функция в
функции в данном направлении. Если
l
u
( M 0 ) 0, то возрастает, при
этом направлении убывает, если
l
u
( M 0 ) – мгновенная скорость изменения функции в
этом
l
заданном направлении в точке М0. Для того чтобы
охарактеризовать направление, в котором функция возрастает
быстрее всего, вводится понятие градиента.
82
!
83.
Опр. 2. Градиентом функции u u( x; y; z ) называется вектор,координаты которого равны соответствующим частным
производным функции:
u u
u
grad u i
j k.
x
y
z
!
Соответственно, для функции z f ( x; y ) двух переменных
z
z
j.
градиент – это вектор grad z i
x y
!
Основные свойства градиента.
1. Производная по направлению вектора l равна скалярному
произведению градиента и единичного вектора этого направления:
u
grad u el ,
l
где el l , el 1.
83
84.
Посколькуu
grad u el grad u el cos grad u cos ,
l
где (grad u; l ) – угол между векторами gradu и l , то несложно
видеть, что производная по направлению принимает наибольшее
значение при cos 1, т. е. если берется в направлении градиента.
2. Градиент
указывает
направление
наискорейшего
возрастания функции.
3. Производная в направлении градиента равна модулю
u
градиента:
grad u , если l grad u.
l
Упражнение. Доказать свойство 3.
4. Градиент в каждой точке направлен перпендикулярно
поверхности (линии) уровня, проходящей через эту точку.
84
85.
Пример 2. Построим линии уровня функции z x 2 y 2 иградиент в точках (1; 0), (0;1), (1;1), ( 1;1).
Решение. Линиями уровня функции z x 2 y 2 являются
концентрические окружности x 2 y 2 c. При c 1 получаем
окружность радиуса 1, которая проходит через точки (1; 0), (0;1);
при c 2 линия уровня проходит через точки (1;1), ( 1;1) .
grad z 2 xi 2 y j
Вычислим градиент:
и построим векторы
grad z (1; 0) 2i;
grad z (1;1) 2i 2 j;
grad z (0;1) 2 j;
grad z ( 1;1) 2i 2 j.
Перпендикулярность градиента функции z x y линиям уровня
2
2
85
86.
Электростатическое поле, т.е. электрическое поле неподвижныхзарядов, можно описать с помощью скалярной функции u(M),
которая называется потенциалом этого поля. Напряженность
электрического поля выражается формулой:
E M grad u M
Пусть электростатическое
поле создается точечным
зарядом е помещенным в
начале координат.
Потенциал поля в
производной точке:
e
u M k
r
где постоянная k зависит от выбора системы единиц,
r x2 y 2 z 2
расстояние от точки М до заряда.
86
87.
Для напряженности электрического поля получаем:1
1
1
e
E ( M ) grad k ke i j k
z r
r
x r y r
ke
x
y
z
i
j
k
2
2
2 3
2
2
2 3
2
2
2 3
x y z
x y z
x y z
ke
ke
3 xi y j zk 3 r
r
r
Значит, вектор электрической напряженности коллинеарен
вектору r
87
88.
ФОРМУЛА ТЕЙЛОРА ДЛЯ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХПусть функция двух переменных z=f(x,y) непрерывна со
всеми своими частными производными до третьего порядка
включительно в некоторой окрестности точки М(хо,уо),
тогда для этой функции формула Тейлора имеет вид
f x; y f x0 ; y0 f x x0 ; y0 x x0 f y x0 ; y0 y y0
1
2
2
f xx x0 ; y0 x x0 2 f xy x0 ; y0 x x0 y y0 f yy x0 ; y0 y y0
2!
x x0 y y0
2
2
u x y , x 0, y R,M 0 1;0
y 2
y 1
f
y
y
1
x
f
yx
0
f 1;0 1 x
1;0 0
xx
1;0
Пример.
y
2
y
f
x
ln
x 1;0 0
f y x ln x 1;0 0 yy
f xy yx y 1 ln x x y 1
1;0
1
88
89.
12
x 1 0 x 1 0 y 0
0 x 1 2 1 x 1 y 0 y 2 r2
2!
1
1 2 x 1 y r2 1 xy y r2
2!
y
u x y , x 0, y R,M 0 1;0
f 1;0 1 f x yx y 1 1;0 0 f xx y y 1 x y 2 1;0 0
Пример.
y
2
y
f
x
ln
x 1;0 0
f y x ln x 1;0 0 yy
f xy yx y 1 ln x x y 2
1;0
1
89
90.
§ 6. Экстремум функции двух переменныхПусть функция z f ( x; y ) определена в точке M 0 ( x0 ; y0 ) и
некоторой ее окрестности.
Опр. 1. Точка M 0 ( x0 ; y0 ) называется точкой локального
максимума (минимума) функции z f ( x; y ), если для всех точек
M ( x; y) из некоторой проколотой окрестности точки M 0 ( x0 ; y0 )
f ( x0 ; y0 ) f ( x; y )
имеет
место
(соответственно
f ( x0 ; y0 ) f ( x; y )).
Характерное свойство точек экстремума: в некоторой
окрестности точки экстремума приращение функции не меняет
знак, а именно z 0 в окрестности точки локального максимума
и z 0 в окрестности точки локального минимума.
Максимум и минимум функции называются экстремумами
функции, т.е. функция имеет экстремум в точке, если в этой
точке она имеет либо максимум, либо минимум.
Точки, в которых функция достигает экстремума, называются
90
точками экстремума.
91.
Т 1 [необходимое условие существования локальногоэкстремума]. Если ( x0 ; y0 ) – точка локального экстремума
функции z f ( x; y ), то в этой точке обе частные производные
f x ( x0 ; y0 ), f y ( x0 ; y0 ) равны 0 или хотя бы одна из них не
существует.
Доказательство следует из аналогичной теоремы для
функций одной переменной.
Рассмотрим функцию z f ( x; y0 ) при фиксированном y y0 .
Это функция одной переменной, x0 – ее точка экстремума,
следовательно, производная этой функции в точке экстремума
f x ( x0 ; y0 ) равна 0 или не существует.
Аналогично доказывается, что f y ( x0 ; y0 ) равна 0 или не
существует.
91
92.
Опр. 2. Точки, в которых выполняется необходимое условиеэкстремума (обе частные производные f x ( x0 ; y0 ), f y ( x0 ; y0 ) равны 0
или хотя бы одна из них не существует), называются
критическими, а точки, в которых f x ( x0 ; y0 ) f y ( x0 ; y0 ) 0, –
стационарными точками функции z f ( x; y ).
Следствие. Если функция u=f(x) дифференцируема в точке M0
и имеет в этой точке локальный экстремум, то
u
u
u
du M 0 M 0 dx M 0 dy M 0 dz 0
x
y
z
Замечание. Условие du(M0)=0 является только необходимым
условием, но не достаточным.
Пример.
z
z
y
0
Пусть z=xy M0(0,0), тогда
x 0,0 0
0,0
x
y
Однако в точке (0;0) экстремума у данной функции нет.
92
93.
Т 2 [достаточное условие существования локальногоэкстремума Ф2П]. Пусть M 0 ( x0 ; y0 ) – стационарная точка
функции z f ( x; y ) и в окрестности этой точки функция имеет
непрерывные частные производные второго порядка. Обозначим
f xx ( x0 ; y0 )
f xy ( x0 ; y0 )
f xy ( x0 ; y0 )
.
f yy ( x0 ; y0 )
Тогда:
1) если 0 и f xx ( x0 ; y0 ) 0, то точка M 0 ( x0 ; y0 ) – точка
локального минимума функции z f ( x; y);
2) если 0 и f xx ( x0 ; y0 ) 0, то точка M 0 ( x0 ; y0 ) – точка
локального максимума функции z f ( x; y);
3) если 0, то точка M 0 ( x0 ; y0 ) не является точкой
локального экстремума функции z f ( x; y);
4) в случае 0 экстремум в точке M 0 ( x0 ; y0 ) может быть,
может не быть; требуются дополнительные исследования.
93
94.
Пример 1. Исследуем на экстремум функцию z x3 y 3 9 xy.Решение. Найдем частные производные первого порядка
z x 3x 2 9 y;
z y 3 y 2 9 x,
приравняем их к 0 и решим систему:
x2
y ,
3
y 2 3 x 0;
3x 2 9 y 0,
z x 0,
2
z
0;
3 y 9 x 0;
y
x2
2
x
y
,
y ,
3
3
4
x 3 x 0;
x 4 27 x 0.
9
Из последнего уравнения получим x( x3 27) 0, откуда
x1 0; x2 3. Тогда соответствующие значения y равны
y1 0; y2 3.
Получили две стационарные точки M 1 (0; 0), M 2 ( 3; 3).
94
95.
Проверим в каждой из этих точек достаточное условие экстремума. Найдемчастные производные второго порядка
z xx 6 x;
и составим определитель
z yy 6y
z xy 9;
6x
9
9
6y
36 xy 81.
Для точки M 1 (0; 0) имеем ( M 1 ) 81 0, т. е. точка M 1 (0; 0) не
является точкой локального экстремума функции.
В точке M 2 ( 3; 3) получим ( M 2 ) 36 9 81 243 0;
z xx ( 3; 3) 18 0, поэтому точка M 2 ( 3; 3) является точкой
локального максимума, значение функции в этой точке равно
zmax zmax ( 3; 3) ( 3)3 ( 3)3 9 ( 3) ( 3) 27.
95
96.
Пример 2. Исследуем на экстремум функцию z 3x 2 y x3 y 4 .Решение. Найдем частные производные первого порядка
z y 3x2 4 y3 ,
z x 6 xy 3x 2 ;
приравняем их к 0 и решим систему:
z x 0,
z y 0;
6 xy 3x 2 0,
2
3
3x 4 y 0;
3x 0,
2
3
3
x
4
y
0;
2 y x 0,
3x 2 4 y 3 0;
3 x(2 y x) 0,
2
3
3
x
4
y
0;
x 0,
3
4
y
0;
x 2 y,
3 4 y 2 4 y 3 0;
x 0,
y 0;
x 2 y,
2
4 y (3 y ) 0;
x 0, y 0;
y 0, x 0;
y 3, x 6.
Получили две стационарные точки M 1 (0; 0), M 2 (6; 3).
96
97.
Проверим в каждой из этих точек достаточное условие экстремума. Найдемчастные производные второго порядка
z xy 6 x;
z xx 6 y 6 x;
z yy 12 y 2
и составим определитель
6 y 6x
6x
6x
12 y
12 6 y 2 ( y x) 36 x 2 36(2 y 2 ( y x) x 2 ).
2
В точке M 2 (6; 3) получим
( M 2 ) 36 (2 9 ( 3) 36) 36 ( 18) 0;
z xx (6; 3) 18 36 18 0,
поэтому точка M 2 (6; 3) является точкой локального максимума,
значение функции в этой точке равно
zmax zmax (6; 3) 3 36 3 63 34 33 (12 8 3) 27.
97
98.
Для точки M 1 (0; 0) имеем ( M 1 ) 0, нужны дополнительныеисследования. Рассмотрим приращение функции в точке M 1 :
z f (0 x; 0 y ) f (0; 0) f ( x; y ) 0 3 x 2 y x3 y 4 .
Заметим, что при y 0 если x 0, то z 0, а если x 0,
то z 0, т. е. в окрестности точки M 1 (0; 0) приращение функции
принимает как положительные, так и отрицательные значения.
Следовательно, в точке M 1 (0; 0) экстремума нет.
98
99.
Т 3 [достаточное условие существования локального экстремумаM 0 ( x10 ; x20 ; ...; xn0 ) – стационарная точка функции
u u ( x1; x2 ; ...; xn ), т. е.
u x1 ( M 0 ) u x2 ( M 0 ) ... u xn ( M 0 ) 0,
и пусть в окрестности этой точки функция u u ( x1; x2 ; ...; xn ) имеет
ФНП].
Пусть
непрерывные частные производные второго порядка. Тогда:
1) если d u ( M 0 ) 0 при всех наборах значений x1 , x2 , ..., xn , не
2
0
0
0
равных 0 одновременно, то точка M 0 ( x1 ; x2 ; ...; xn ) является точкой
локального минимума функции u u ( x1; x2 ; ...; xn );
2
2) если d u ( M 0 ) 0 при всех наборах значений x1 , x2 , ..., xn , не
0
0
0
равных 0 одновременно, то точка M 0 ( x1 ; x2 ; ...; xn ) является точкой
локального максимума функции u u ( x1; x2 ; ...; xn );
2
3) если d u ( M 0 ) принимает как положительные, так и отрицательные
0
0
0
значения, то точка M 0 ( x1 ; x2 ; ...; xn ) не является точкой локального
экстремума функции u u ( x1; x2 ; ...; xn );
99
100.
4) если при всех наборах значений x1 , x2 , ..., xn имеет местоd 2u ( M 0 ) 0 либо d 2u ( M 0 ) 0, причем существуют такие наборы
значений x1 , x2 , ..., xn , не равных 0 одновременно, что d u ( M 0 ) 0, то
2
вопрос о существовании локального экстремума функции u u ( x1; x2 ; ...; xn )
0
0
0
в точке M 0 ( x1 ; x2 ; ...; xn ) остается открытым; требуются дополнительные
исследования.
Замечание. Отметим, что дифференциал второго порядка ФНП
2
2
u
u
2
2
d u 2 xi 2
xi x j
i 1 xi
i j xi x j
n
является квадратичной формой от величин x1 , x2 , ..., xn . Достаточные
условия существования локального экстремума ФНП могут быть
переформулированы как условия знакоопределенности квадратичной формы,
проверка которых в теории квадратичных форм проводится с помощью
критерия Сильвестра.
100
101.
Понятие об условном экстремумеЭкстремум функции z f ( x; y ), найденный при условии, что
( x; y) 0, называется условным, а уравнение ( x; y) 0
называется уравнением связи. В отличие от обычной (безусловной)
точки экстремума, значение функции в точке условного экстремума
сравнивается с ее значениями не во всех точках некоторой
окрестности, а только в тех, для которых выполняется условие
связи ( x; y) 0.
Пример 3. Найдем экстремум функции z x 2 y 2 при условии
x y 1.
Решение. Выражая из уравнения связи y 1 x и подставляя По
это выражение в функцию z, сводим задачу к поиску безусловного ня
ти
экстремума функции одной переменной
z x (1 x) ;
2
2
z 2 x 2 x 1.
2
101
е
об
ус
ло
вн
102.
Находя производную и приравнивая ее к 0:z 4 x 2 0,
1
получим критическую точку x . Воспользуемся достаточным
2
условием экстремума на основании второй производной: так как
1
1
z 4 0, то критическая точка x
является точкой
2
2
локального
минимума
функции
причем
z 2 x2 2 x 1,
1
1
1
1
zmin z 2 2 1 .
4
2
2
2
Определим вторую координату точки условного экстремума:
1 1
y 1 . Следовательно, функция z x 2 y 2 при условии
2 2
1
x y 1 имеет условный локальный минимум zmin в точке
2
1 1
M ; .
2 2
102
103.
Замечание. Функция z x y задает в пространстве эллиптическийпараболоид .
2
2
Условный экстремум функции z x y при условии x y 1
2
2
Несложно видеть, что безусловный минимум этой функции достигается в
точке O(0; 0) и равен zmin z (0; 0) 0. 2
2
Условный минимум функции z x y при условии x y 1 – это
минимум на линии пересечения параболоида и плоскости
x y 1
(см. рис. 12).
103
104.
В случае, когда уравнение связи сложно разрешитьотносительно какой-либо переменной или когда это приводит к
громоздким вычислениям, для нахождения критических точек
используется метод множителей Лагранжа.
Пусть требуется найти экстремум функции z f ( x; y ) при
условии, что ( x; y) 0, т. е.
f ( x; y ) extr,
( x; y ) 0.
104
105.
Метод множителей Лагранжа включает следующие этапы:1) составить функцию Лагранжа
L( x; y; ) f ( x; y) ( x; y);
2) найти критические точки как критические точки функции
Лагранжа, т. е. решить систему
Lx ( x; y; ) 0,
L y ( x; y; ) 0,
L ( x; y; ) 0;
3) определить знак приращения z в окрестности критических
точек по тем точкам окрестности, которые удовлетворяют
уравнению связи ( x; y) 0.
Замечание. При решении конкретных задач иногда удается
установить характер критических точек на основании существа
задачи.
105
106.
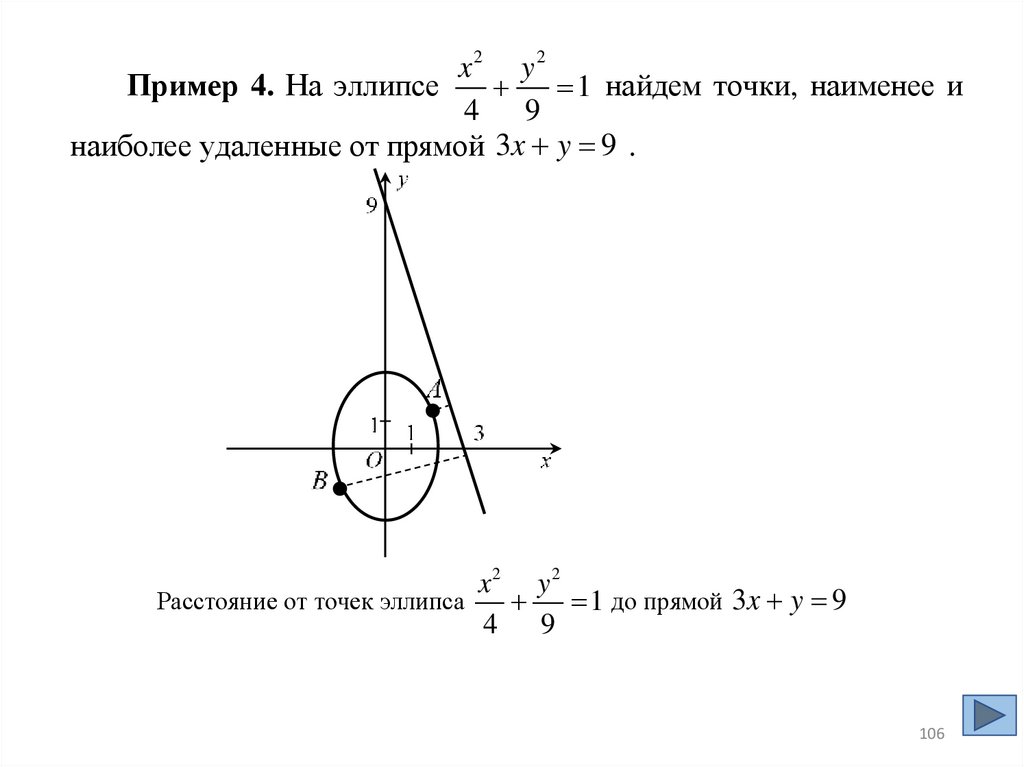
x2 y 2Пример 4. На эллипсе
1 найдем точки, наименее и
4 9
наиболее удаленные от прямой 3x y 9 .
x2 y 2
Расстояние от точек эллипса
1 до прямой 3x y 9
4 9
106
107.
Решение. Запишем формулу, выражающую расстояние отпроизвольной точки ( x; y ), лежащей на эллипсе, до прямой:
d ( x; y )
| 3x y 9 |
32 12
Имеем задачу условного экстремума
или, что эквивалентно, задачу
| 3x y 9 |
.
10
d ( x; y ) extr,
2
x
y2
1,
9
4
f ( x; y ) 10d 2 ( x; y ) (3x y 9) 2 extr,
2
x
y2
1 0.
9
4
Составим функцию Лагранжа
2
2
x
y
2
L( x; y; ) (3x y 9)
1
9
4
107
108.
найдем критические точки из условия равенства нулю частных производныхфункции Лагранжа:
Lx ( x; y; ) 0,
L y ( x; y; ) 0,
L ( x; y; ) 0;
x
6
(3
x
y
9)
0,
2
2 y
0,
2(3 x y 9)
9
x2 y 2
1 0.
9
4
Для решения системы выразим из первого и второго
x
y
уравнений 3x y 9 ; 3x y 9 , откуда получим
12
9
x y
4y
. Следовательно, либо 0, либо x .
12 9
3
3 x y 9 0,
При 0 получим систему x 2 y 2
которая не имеет
1,
9
4
решений, так как прямая и эллипс не пересекаются.
108
109.
4y, то подставляя это соотношение в уравнение
3
4
3
5 y2
16 y 2 y 2
x
.
y
;
1; 2
1; 2
1;
эллипса, получим
1;
5
5
9
9 4
9
3
4
4 3
получили две критические точки A
и
B
;
;
.
5
5
5 5
(Заметим, что значение можно однозначно определить из
первого или второго уравнений системы, но необходимости в этом
нет.)
Если x
Вычислим значение расстояния до прямой для каждой из критических точек:
4
3
9 3 5 9
9 3 5
4 3
5
5
;
d ( A) d
;
10
10
10
5 5
4
3
3
9 3 5 9
3
4
9 3 5
5
5
d ( B) d ;
.
5
10
10
10
5
3
4 3
Т.о. точка A
;
наименее удалена от прямой, а точка
5 5
3
4
B
;
– наиболее.
5
5
109
110.
Нахождение наименьшего и наибольшего значений(глобальных экстремумов) функции двух переменных в
области
Для ФНП, как и для функций одной переменной, справедлива
теорема Вейерштрасса.
Т 4 [Вейерштрасса]. Если ФНП непрерывна в замкнутой
ограниченной области, то она ограничена в этой области и
достигает в ней наибольшего и наименьшего значений.
Эти значения (глобальные экстремумы функции в области)
достигаются либо в точках локального экстремума,
расположенных внутри области, либо на границе этой
области.
!
110
111.
Таким образом, для нахождения наибольшего и наименьшегозначений ФНП в области нужно:
1) найти критические точки функции и выбрать те, которые
входят в область;
2) найти наименьшее и наибольшее значения функции на
границе области;
3) сравнить все найденные значения функции и выбрать из
них наименьшее и наибольшее.
111
!
!
112.
Пример 5. Найдем наименьшее и наибольшее значенияx2
3
2
функции z 2 x 6 xy 3 y в области D : y 2; x 0.
2
Решение. Построим область D.
Найдем критические точки. Для этого найдем частные производные первого
2
порядка
6 x 6 y,
6
x
6 y;
x
y
приравняем их к 0 и решим систему:
z
z x 0,
z y 0;
z
6 x 2 6 y 0,
6 x 6 y 0;
x 2 y 0,
x y.
x2 x 0; x( x 1) 0,
откуда x1 0; x2 1, а значит, y1 0; y2 1, т. е. имеем две
критические точки O(0; 0) и М (1;1).
Обе эти точки принадлежат области D: точка O(0; 0) лежит на
границе области, а точка М (1;1) внутри области
Получим
112
113.
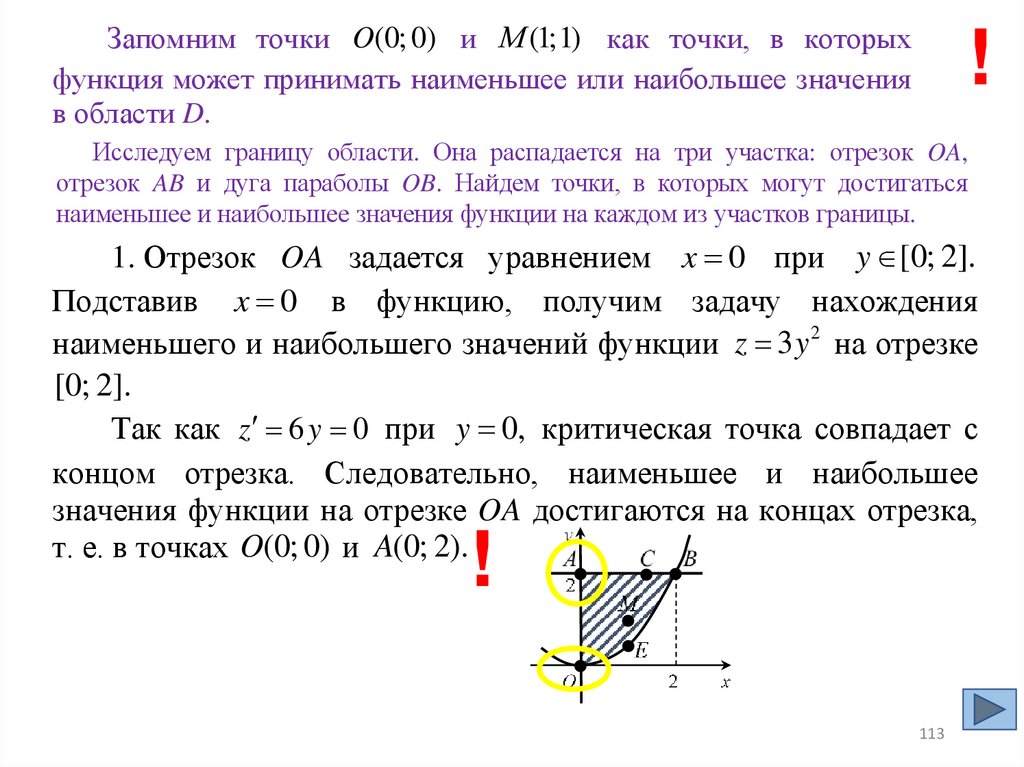
Запомним точки O(0; 0) и М (1;1) как точки, в которыхфункция может принимать наименьшее или наибольшее значения
в области D.
!
Исследуем границу области. Она распадается на три участка: отрезок OA,
отрезок AB и дуга параболы OB. Найдем точки, в которых могут достигаться
наименьшее и наибольшее значения функции на каждом из участков границы.
1. Отрезок OA задается уравнением x 0 при y [0; 2].
Подставив x 0 в функцию, получим задачу нахождения
наименьшего и наибольшего значений функции z 3 y 2 на отрезке
[0; 2].
Так как z 6 y 0 при y 0, критическая точка совпадает с
концом отрезка. Следовательно, наименьшее и наибольшее
значения функции на отрезке OA достигаются на концах отрезка,
т. е. в точках O(0; 0) и A(0; 2).
!
113
114.
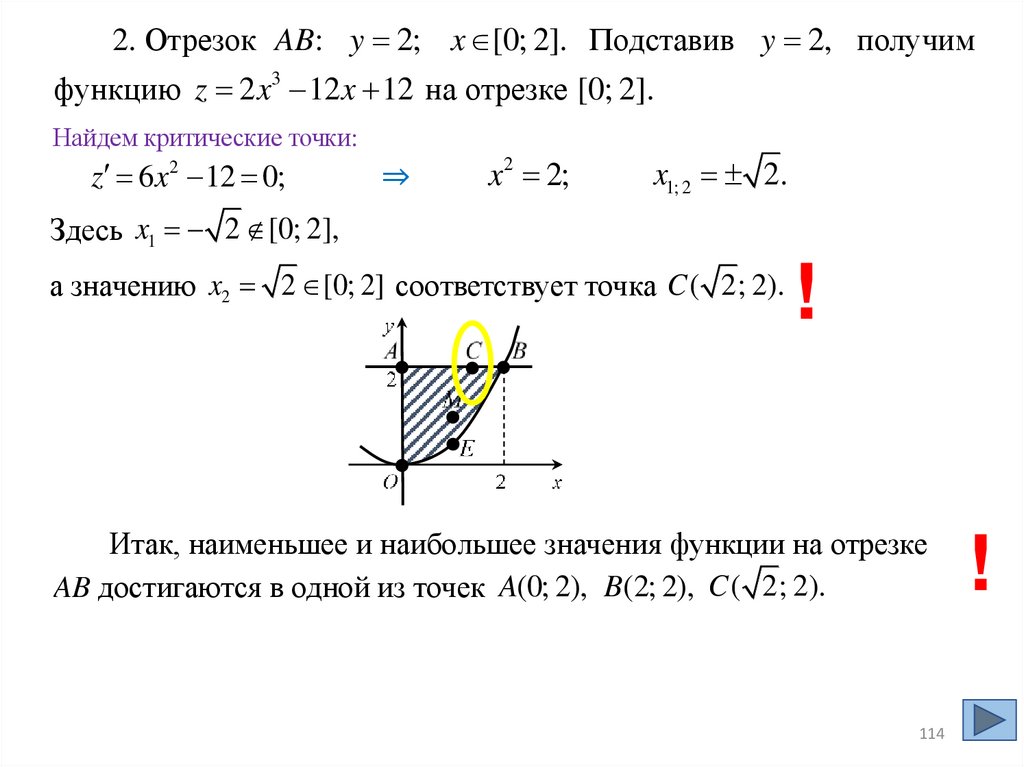
2. Отрезок AB: y 2; x [0; 2]. Подставив y 2, получимфункцию z 2 x3 12 x 12 на отрезке [0; 2].
Найдем критические точки:
z 6 x2 12 0;
֜
x2 2;
x1; 2 2.
Здесь x1 2 [0; 2],
а значению x2 2 [0; 2] соответствует точка C ( 2; 2).
!
Итак, наименьшее и наибольшее значения функции на отрезке
AB достигаются в одной из точек A(0; 2), B(2; 2), C ( 2; 2).
114
!
115.
x23. Дуга OB: y ; x [0; 2].
2
x2
Подставив y ; получим функцию
2
2
2
3 4
x
x
3
z 2 x 6 x 3 x x3
2
2 4
2
Найдем критические точки:
z 3x3 3x2 0;
֜
на отрезке [0; 2].
3x 2 ( x 1) 0,
откуда x1 0; x2 1.
Обе точки принадлежат отрезку [0; 2].
1
x2
Поскольку эти точки лежат на параболе y , то y1 0; y2 .
2
2
1
Следовательно, это точки O(0; 0) и E 1; .
2
!
115
116.
Таким образом, наименьшее и наибольшее значения функции1
на отрезке OB достигаются в одной из точек O(0; 0), E 1; ,
2
B(2; 2).
Найдем значения функции во всех полученных точках:
z (O) z (0; 0) 0;
z ( A) z (0; 2) 0 0 12 12;
z ( B) z (2; 2) 16 24 12 4;
z (C ) z ( 2; 2) 4 2 12 2 12 12 8 2;
1
3
1
z ( E ) z 1; 2 3 .
4
4
2
Поскольку 12 8 2 12
делаем вывод:
и 12 8 2 8 (1,5 2) 0,
то
наименьшее значение функции в области D равно
zнаим z (1;1) 1, наибольшее значение zнаиб z (0; 2) 12.
116
117.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВПусть в результате эксперимента получено n значений
функции у . Результаты записаны в таблицу:
Х
Y
х1
y1
х2
y2
х3
y3
...
...
хn
yn .
Требуется
на
основании
эксперимента
установить
функциональную зависимость величины у от величины х, т.е.
подобрать функцию у=у(х).
Данную задачу рекомендуется решать в два этапа.
На первом этапе устанавливается вид функции. Это делается
либо из теоретических соображений, либо на основании
характера расположения на координатной плоскости точек,
соответствующих экспериментальным данным.
На втором этапе определяются параметры функции , чтобы
искомая функция в каком-то смысле наилучшим образом
описывала рассматриваемый процесс. Такие задачи, как
117
правило, решаются методом наименьших квадратов.
118.
Рассмотрим идею этого метода на примере линейной функциивида у=ах+b, т.е. как по экспериментальным данным
подбирают параметры а и b.
Рассмотрим сумму квадратов разностей значений уi ,
полученных при эксперименте, и функции у=ах+b в
соответствующих точках :
n
S a, b ( yi (axi b)) 2 .
i 1
Подбираем параметры а и b так, чтобы эта сумма имела
наименьшее значение, поскольку представляет собой
погрешность при такой замене.
Таким образом, задача сводится к нахождению значений
параметров а и b, при которых функция S(а,b) имеет минимум,
Следовательно,
частные
производные
при
искомых
параметрах обращаются в нуль. Получим S/ а=0;
или в развернутом виде
S/ b=0
118
119.
nS
yi axi b xi 0
a 2
i 1
n
S
2 y ax b 1 0
i
i
b
i 1
или
n
n
n 2
xi b xi xi yi
a
i 1
i 1
i 1
n
n
a xi bn yi
i 1
i 1
Получена система двух линейных уравнений с двумя
неизвестными а и b. Очевидно, что система имеет
определенное решение и что при полученных значениях а и b
функция S(а,b) имеет минимум.
Пример.
Д.И. Менделеев в труде «Основы химии» приводит данные
растворимости у натриевой селитры NaNO3 на 100 г воды в
зависимости от температуры
119
120.
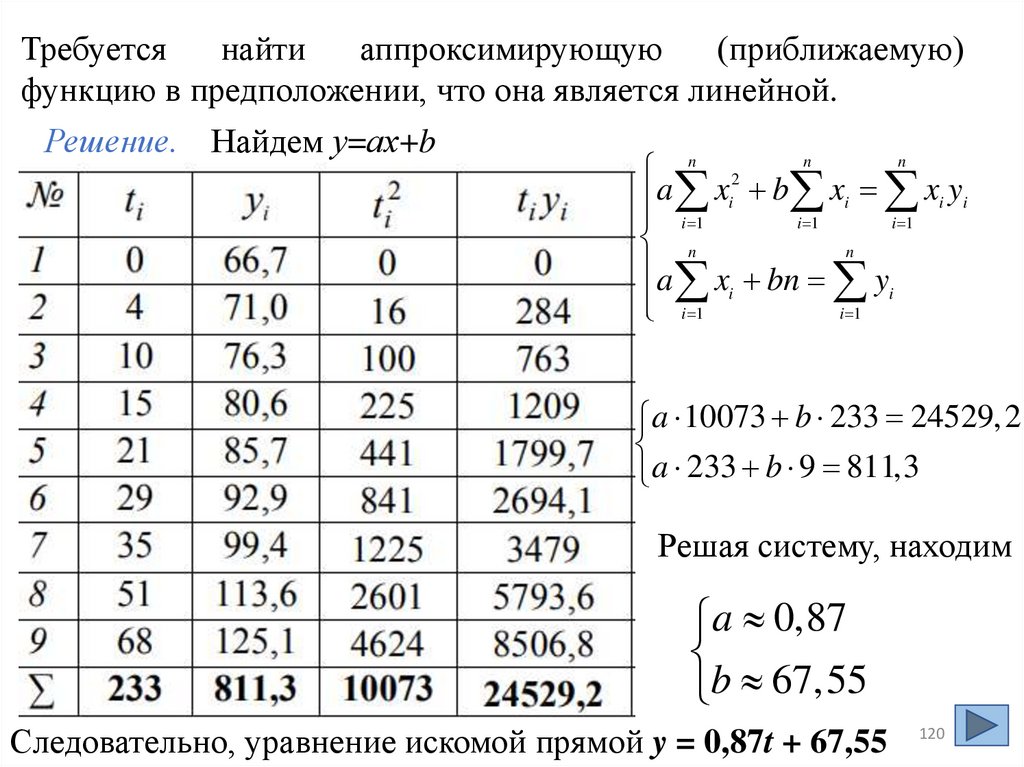
Требуетсянайти
аппроксимирующую
(приближаемую)
функцию в предположении, что она является линейной.
Решение. Найдем у=ах+b
n
n
n 2
xi b xi xi yi
a
i 1
i 1
i 1
n
n
a xi bn yi
i 1
i 1
a 10073 b 233 24529,2
a 233 b 9 811,3
Решая систему, находим
a 0,87
b 67,55
Следовательно, уравнение искомой прямой y = 0,87t + 67,55
120






















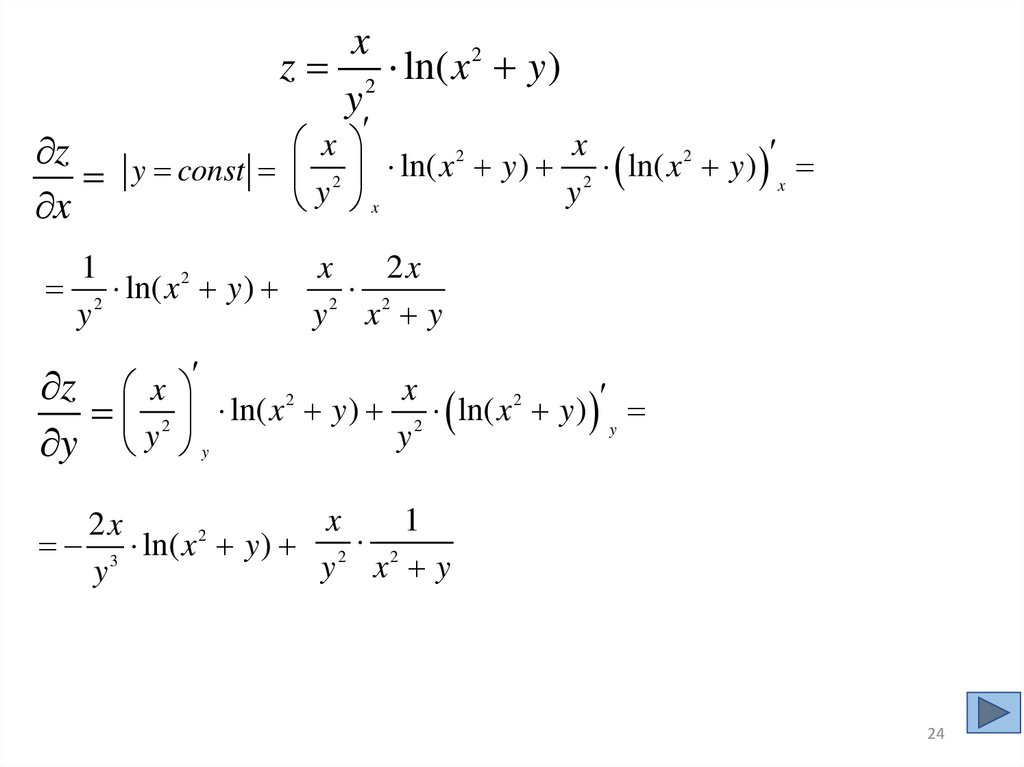





















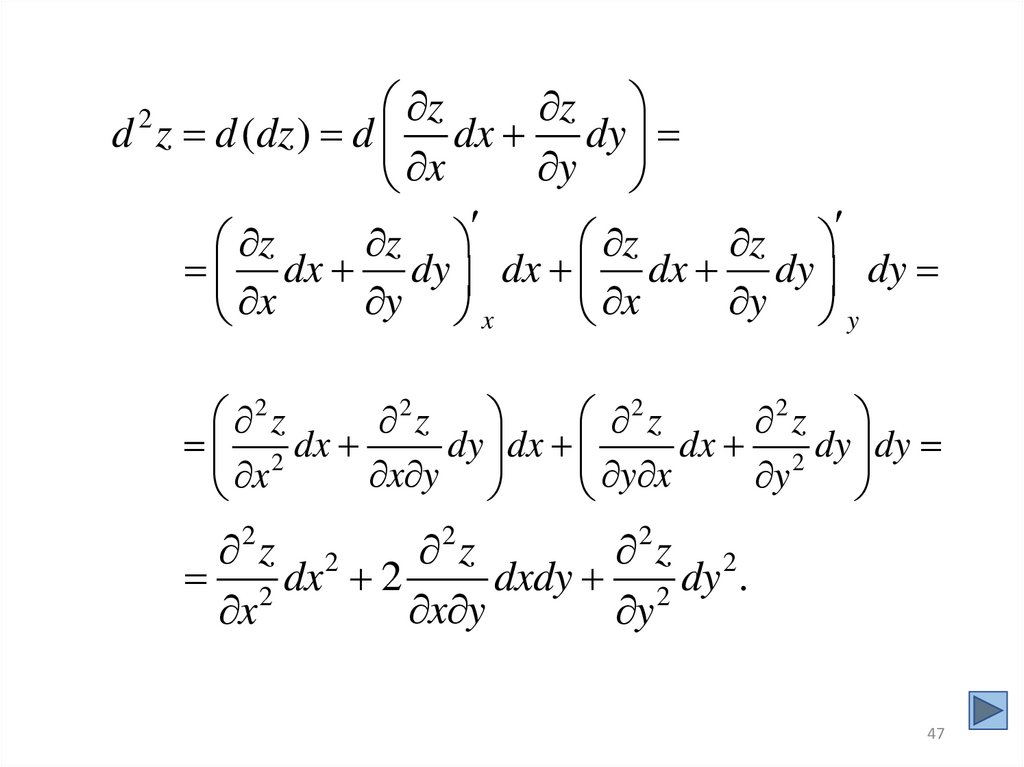




































































 Математика
Математика








