функции пределы функций

2.

Понятие функции. Основные
свойства и классификация

Определение.
Функция – математическое понятие, отражающее связь между
элементами различных множеств; «закон», по которому каждому
элементу одного множества X ставится в соответствие один и
только один элемент другого множества Y (X отображается в Y ):
Определение.
Определение.
Множество
X значению
называется
областью Xопределения
(задания)
Если
каждому
х множества
(x X) ставится
в соотПравило
каждому
хзначений
X YR(y Y),
единстветствие
вполне
определенное
учислу
множества
то
функции
у =f, fсопоставляющее
(х),
а множествозначение
Y – областью
(измевенное число
R, называется
говорят,
что нау Y
множестве
X задана функцией
функция уу== f (х),
). заданной на
нения) функции
.
множестве
X и принимающей
значения в множестве
Y. Под ред.
«Высшая
математика
для хэкономического
бакалавриата».
При
этом
переменная
называется
аргументом
функции
проф.
Кремера
Н.Ш.
Ахтямов
А. М.
«Математика для социологов и экономистов».
или независимой переменной, а элемент у, соответствующий
Определение.
конкретному
элементу х – значением функции у = f (х) в точке х.
Пусть X и Y - некоторые числовые подмножества множества R
Замечание.
Пример.
и
каждому элементу x X по какому-либо закону f поставлен в
Если множество
специально
не
то под
областью
Область
определения
функции y Y
y = оговорено,
x.2 + √10 - x есть
полуинтерсоответствие
только X
один
элемент
Тогда
определена
функциональная
зависимость
y от xзнапо
определения
функции
подразумевается
область
допустимых
вал
(- ,10],
так
как 10
- x ≥ 0. Если же переменная
x, например,
закону
у = f (хвремя,
).
обозначает
то областью
чений
независимой
переменной
х. определения функции будет
Красс, [0,10].
М.С. Чупрынов Б. П. «Математика для экономистов».
отрезок

4.

Способы задания функции
1. Аналитически – формулой, связывающей элементы x и y:
а) в явном виде; б) в неявном виде; в) параметрически;
г) в виде обратной функции; д) в виде сложной функции.
2. Графически – в виде изображения графика
функции на координатной плоскости, в котором
аргументу х соответствует ось абсцисс,
а значению функции y - ось ординат.
y=2x+1
y
y
(x,y)
1
x
3. Таблицей:
0
x 1
4. Алгоритмом ее вычисления или составления (в том числе
вербально), например, функция Дирихле.
5. Рекурсивно – когда одни значения функции определяются
через другие ее значения, например: n! = (n-1)!·n.

5.

Основные свойства функций
Определения.
1. Функция у = f(х) называется четной, если для любых значений х из области определения функции f(-х) = f(х), и нечетной,
если f(-х) = -f(х).
В противном случае у = f(х) – функция общего вида.
2*.
Функция уу==f(х)
f (х)называется
называетсявозрастающей
неубывающей (невозраста2. Функция
(убывающей)
ющей)
на некотором
промежутке
на некотором
промежутке
X, еслиX, если
x11 , x22 X таких, что x11 x22 ( x11 x22) f ( x11) f ( x22) ( f ( x11) f ( x22)).
Возрастающие или
или невозрастающие
убывающие функции
называются
строго
Неубывающие
функции
называются
момонотонными.
нотонными.
3. Функция
(снизу) на
3*.
Функция ff(х)
(х) называется
называется ограниченной
ограниченной сверху
на промежутке
X,
промежутке
X, если
если
существует
такое число M > 0, что | f(х)| ≤ M, для всех х X.
В противном
случае
функция
M (m
) такие,
что xназывается
X f ( xнеограниченной.
) M ( f ( x) m ).
4. Функция у = f(х) называется периодической с периодом Т ≠ 0,
если f (х + Т ) = f (х) для любых х X.

6.

Предел функции. Основные
теоремы о пределах

7.

Определение
Число A называется пределом функции f (х) в точке х0, если
для любой последовательности точек
, сходящейся к х0, но
не содержащей х0 в качестве одного из своих элементов (т.е. в
окрестности
х0),
последовательность
значений
функции
сходится к A:

8.

Определение.
Число A называется левым (правым) пределом функции f (х)
в точке х0, если для любого наперед взятого числа ε > 0 найдется
отвечающее ему число δ = δ(ε) > 0 такое, что для всех х ≠ х0 и удовлетворяющих условию х0 - δ < х < х0 ( х0 < х < х0 + δ ), выполняется
неравенство | f (x) – A | < ε:
lim f ( x) A 0 ( ) 0 x ( x0 , x0 ) | f ( x) A | ;
x x0 0
lim f ( x) A 0 ( ) 0 x ( x0 , x0 ) | f ( x) A | .
x x0 0

9.

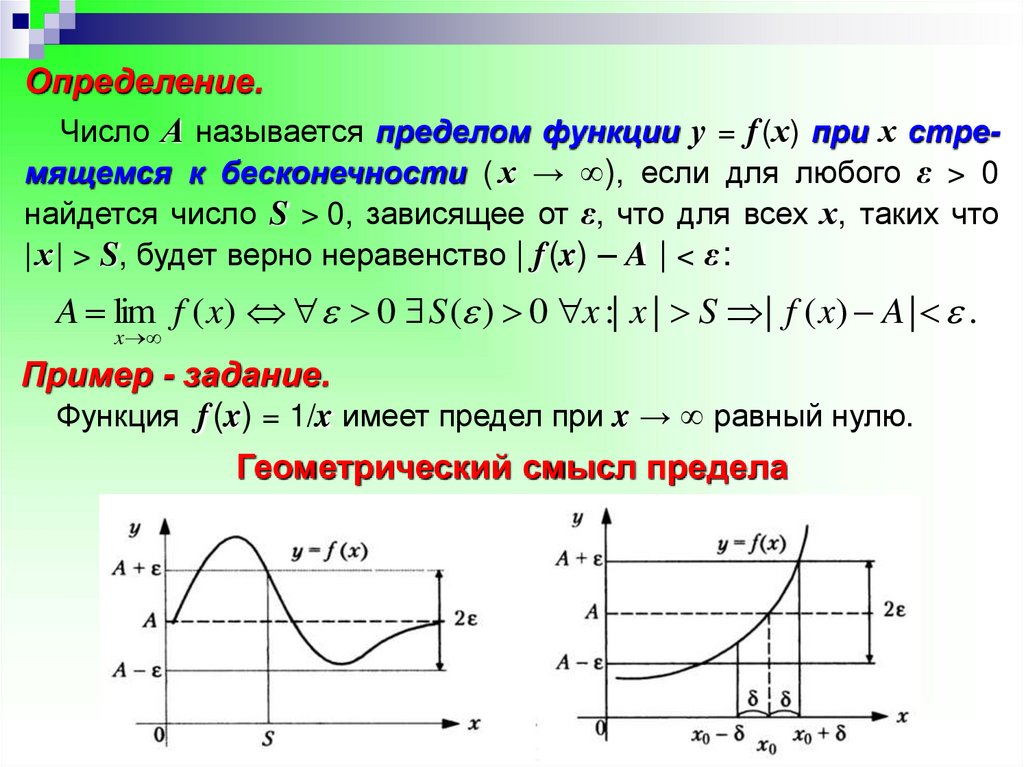
Определение.
Число А называется пределом функции у = f (х) при х стремящемся к бесконечности ( х → ), если для любого ε > 0
найдется число S > 0, зависящее от ε, что для всех х, таких что
| х | > S, будет верно неравенство | f(x) – A | < ε:
A lim f ( x) 0 S ( ) 0 x :| x | S | f ( x) A | .
x
Пример - задание.
Функция f (x) = 1/x имеет предел при x → равный нулю.
Геометрический смысл предела
Определение.
Число А называется пределом функции у = f (х) при х → +
( х → - ), если для любого ε > 0 найдется число S > 0, зависящее
от ε, что для всех х > S ( х < - S ), будет верно неравенство
| f(x) – A | < ε.

10.

Свойства бесконечно малых величин
Определение.
Если α(х) и β(х) бесконечно малые величины при х → х0 или
Функция α(х) называется бесконечно малой величиной при
хх →
малыми величинами:
→
х0, то
(х будут
→ ),бесконечно
если ее предел равен нулю:
1. α(х) ± β(х); 2. с∙α(х), с – постоянная; 3. α(х)∙β(х);
lim
(хx)∙α
) (х0), f (
– ограниченная
0 ( ) 0 функция;
x x0 :| x x0 | | ( x) | ;
4.
f
(
х
)
x x0
lim
f (0x) S0( . ) 0 x :| x | S | ( x) | .
5. α((хx)) / f (0х),
lim
x x ( )
x
0
Сравнение порядков бесконечно малых.
Теорема.
Если α(х) и β(х) бесконечно малые величины при х → х0 или
х →Функция
, и lim f (х()x)имеет
/ ( x) kпри
, тох → х0 (х → ) предел, равный А,
x x0 ( )
тогда и только тогда, когда ее можно представить в виде
- при k = 0 бесконечно малая α(х) называется бесконечно малой
суммы этого числа А и бесконечно малой величины α(х) при
более высокого порядка малости, чем β(х);
х → х0 (х → ):
- при k = – более низкого порядка малости, чем β(х);
- при
А
– одного
lim 0 <f (kx<)
f ( xпорядка
) А малости;
( x), где lim ( x) 0.
x0 ( )k = 1 бесконечно малые α(х) и β(х) называются
x x0 ( )
-x при
эквивалентными, например, при х → 0 sin x х; In (1 + х) х; е х 1 + х.

11.

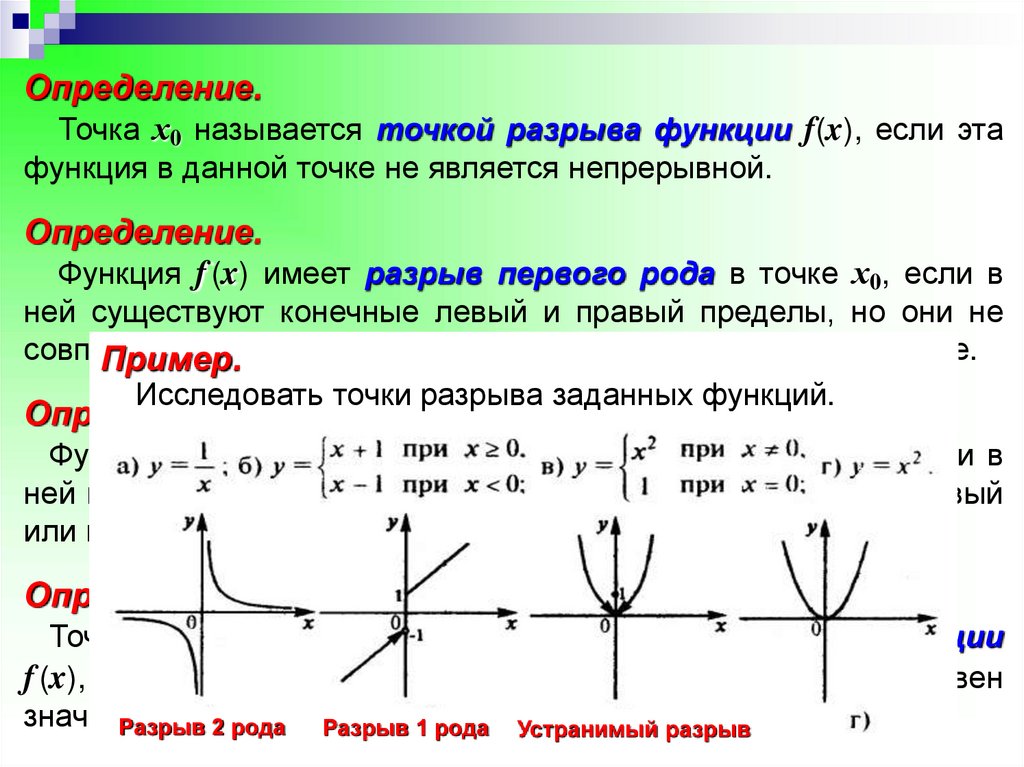
Определение.
Функция f(х)прих → х0 (х → )называетсябесконечно боль-шой
величиной ( lim

English Русский Правила