Функции одной переменной

1.

Российская академия народного хозяйства и
государственной службы при Президенте РФ
Факультет национальной безопасности
Раздел 2 тема № 1
«ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ»
Лекция № 1
профессор Резниченко Александр Васильевич
Москва – 2013

2.

УЧЕБНЫЕ ВОПРОСЫ:
1. Понятие функции. Основные свойства
и классификация
2. Предел функции. Основные теоремы
о пределах
3. Непрерывность функции

3.

Литература
1. «Высшая математика для экономических специальностей». Учебник и Практикум (части I и II) / Под ред.
Н.Ш. Кремера. М.: Высшее образование, 2008.
2. «Математика: Математический анализ. Дифференциальные уравнения. Теория вероятностей. Математическая статистика». Учебно-методическое пособие /
Под ред. А.Н. Данчула. М.: Изд-во РАГС, 2004.
3. Гельман В.Я. «Решение математических задач средствами Excel: Практикум». Учебник для вузов. СПб.:
ПИТЕР, 2003.
4. «Сборник задач по математике». М.: Изд. РАГС, 2005.

4. Литература

ПЕРВЫЙ ВОПРОС
Понятие функции. Основные
свойства и классификация

5.

Определение.
Множество X называется областью определения (задания)
Определение.
функции у = f(х), а множество Y – областью значений (измеЕсли каждому элементу (значению) х множества X R поставнения)
функции . определенный элемент (значение) у множестлен в соответствие
При , этом
переменная
х называется
аргументом
ва Y R
то говорят,
что на множестве
X задана
функцияфункции
у = f(х).
или независимой переменной, а элемент у, соответствующий
конкретному элементу х – значением функции у = f(х) в точке х.
Замечание.
Пример.
Если множество
X специально
то под
областью
Область
определения
функции не
y = оговорено,
x2 + √10 - x есть
полуинтеропределения
функции
область допустимых
знавал (- ,10], так
как 10подразумевается
- x ≥ 0. Если же переменная
x, например,
чений
независимой
х. определения функции будет
обозначает
время, переменной
то областью
отрезок [0,10].

6.

Определение.
Функция называется явной, если она задается формулой у=f(х),
в которой правая часть не содержит зависимой переменной,
например, y = 2x +1.
Определение.
Функция у аргумента х называется неявной, если она задана
уравнением F(x, y) = 0, не разрешенным относительно зависимой
переменной, например, y - 2x - 1 = 0.
Определение.
Параметрическим представлением функции называется
разновидность представления переменных, когда их зависимость
выражается через дополнительную величину – параметр.
Предположим, что функциональная зависимость y от x задана
Пример.
через
промежуточную величину
– t.
Параметрическое
представление
x R cos t ,
Тогда
формулы
x
=
φ
(
t
)
и
y
=
ψ
(
t
)
задают
параметрическое
2
2
верхней полуокружности y = + √R - x имеет вид
представление
функции одной переменной. y R sin t ,
при t [0,π].

7.

Определение.
Пусть у = f(х) есть функция независимой переменной х, определенной на множестве Х с областью значений Y. При этом каждому y Y соответствует единственное значение х Х такое,
что f(х) = у.
Тогда полученная функция x = φ (у),
определенная на множестве Y с областью
значений Х, называется обратной.
Обозначение: у = f -1(х).
Графики взаимно обратных функций симметричны относительно биссектрисы первого
и третьего координатных углов
Определение.
Если функция у = f(u) есть функция переменной u (определенной на множестве U с областью значений Y ), а переменная u, в
свою очередь, также является функцией u = φ (х) (определенной
на множестве X с областью значений U), то заданная на множестве X функция у = f(φ (х)) называется сложной функцией.

8.

Способы задания функции
1. Аналитически – формулой, связывающей элементы x и y:
а) в явном виде; б) в неявном виде; в) параметрически;
г) в виде обратной функции; д) в виде сложной функции.
2. Графически – в виде изображения графика
функции на координатной плоскости, в котором
аргументу х соответствует ось абсцисс,
а значению функции y - ось ординат.
y=2x+1
y
y
(x,y)
1
x
3. Таблицей:
0
x
1
4. Алгоритмом ее вычисления или составления (в том числе
вербально), например, функция Дирихле.
5. Рекурсивно – когда одни значения функции определяются
через другие ее значения, например: n! = (n-1)!·n.

9.

Основные свойства функций
Определения.
1. Функция у = f(х) называется четной, если для любых значений х из области определения функции f(-х) = f(х), и нечетной,
если f(-х) = -f(х).
В противном случае у = f(х) – функция общего вида.
2*.Функция
Функцияуу==f(х)
f (х)называется
называетсявозрастающей
неубывающей (убывающей)
(невозраста2.
ющей)
на некотором
промежутке
на
некотором
промежутке
X, если X, если
f ( x2 ) ( f ( x1 )
f ( x2 )).
x1 , x2 X таких, что x1 x2 ( x1 x2 ) f ( x1 )
Возрастающие
или невозрастающие
убывающие функции
называются
строго
Неубывающие или
функции
называются
момонотонными.
нотонными.
3. Функция
(снизу) на
3*.
Функция ff(х)
(х) называется
называется ограниченной
ограниченной сверху
на промежутке
X,
промежутке
X, если
если
существует
такое число M > 0, что | f(х)| ≤ M, для всех х X.
В противном
случае
функция
M (m
) такие,
что xназывается
X f ( xнеограниченной.
) M ( f ( x) m ).
4. Функция у = f(х) называется периодической с периодом Т ≠ 0,
если f (х + Т) = f (х) для любых х X.

10.

Основные
элементарные
функции:
КЛАССИФИКАЦИЯ
ФУНКЦИЙ
а) степенная функция у = х n;
x, а > 0, ЭЛЕМЕНТАРНЫЕ
б) показательная
функция
у
=
а
а≠1
Алгебраические функции
(X = (- ; +ФУНКЦИИ
); Y = (0; + ));
- целая
рациональная
функцияy = loga x, а > 0, а ≠ 1
в)
логарифмическая
функция
(многочлен или полином);
(X = (0; + ); Y = (- ; + ));
- дробно-рациональная
г)
тригонометрические функция;
функции
- иррациональная функция. y = sin x, y = cos x,
y = tg x, y = ctg x;
Трансцендентные
д) обратные тригонометрические
функции функции
у(неалгебраические)
= arcsin х, у = arccos х,
у = arctg x, у = arcctg х.
- показательная функция;
- логарифмическая функция;
Элементарными называются функции, построенные из
- тригонометрические
функции;
основных элементарных функций
при помощи конечного
числа
тригонометрические
алгебраических действий и- обратные
конечного числа
операций образофункции и т.д.
вания сложной функции.
Определение.

11.

ВТОРОЙ ВОПРОС
Предел функции. Основные
теоремы о пределах

12.

Определение.
Если каждому числу из натурального ряда чисел 1, 2, ..., n, ...
поставлено в соответствие вещественное число xn, то множество
вещественных чисел x1, x2, ..., xn, ... называется числовой последовательностью.
Числа x1, x2, ..., xn, ... называются элементами или членами
Определение.
последовательности,
xn – элементов
общим членом
последовательПоследовательностью
числового
множества R
Примеры.
ности, а число
n – его номером.
называется
отображение
f, определенное на множестве натуа) Обозначение
x
=
const
;
{ x1, x2в,...,
xn, ... }: {{ xRn }}., nт.е.
n чисел N последовательности
1 .
ральных
и принимающее значения
множестве
б) xn = n
т.е. { xn } равна f{ 1,
3, R.
... } – натуральные числа;
: N2,
f называетв)Элементом
xn = 1/n т.е. или
{ xn } членом
равна { 1,последовательности
1/2, 1/3, ... };
ся упорядоченная
пара (п, х), х = f (п), п N, х R.
г) xn = n·(-1)n т.е. { xn } равна { -1, 2, -3, 4, ... }.
Натуральное число п называется номером элемента последовательности, а число х R – его значением.

13.

Определение.
Число А называется пределом последовательности { xn },
если для любого ε 0 существует такое натуральное число N, что
при всех n ≥ N выполняется неравенство │xn - А│ ε:
0 N=N( ) n ≥ N | xn - А | ε.
Определение.
Если последовательность { xn } имеет своим пределом число А,
то символически это записывается так:
xn Α
n
или
lim xn Α.
n
Геометрический смысл предела числовой последовательности
Неравенство │xn – А│ ε равносильно двойному неравенству А – ε xn А + ε.
x1
x3 x5
x7 x9
x8
x6
x4
x2
xn

14.

Определение (предел функции по Гейне).
Число A называется пределом функции f (х) в точке х0, если
для любой последовательности точек
, сходящейся к х0, но
не содержащей х0 в качестве одного из своих элементов (т.е. в
проколотой окрестности х0), последовательность значений функции
сходится к A:
Огюстен Луи Коши
Теорема.
Определения предела функции по Гейне и по Коши эквивалентны.
Определение (предел функции по Коши).
Число A называется пределом функции f(х) в точке х0, если
для любого наперед взятого числа ε > 0 найдется отвечающее ему
число δ = δ(ε) > 0 такое, что для всех х ≠ х0 и удовлетворяющих
Генрих Эдуард Гейне
условию | х-х0 | < δ, выполняется неравенство
:

15.

Определение.
Число A называется левым (правым) пределом функции f (х)
в точке х0, если для любого наперед взятого числа ε > 0 найдется
отвечающее ему число δ = δ(ε) > 0 такое, что для всех х ≠ х0 и удовлетворяющих условию х0 - δ < х < х0 ( х0 < х < х0 + δ ), выполняется
неравенство | f(x) – A | < ε:
lim f ( x) A 0 ( ) 0 x ( x0 , x0 ) | f ( x) A | ;
x x0 0
lim f ( x) A 0 ( ) 0 x ( x0 , x0 ) | f ( x) A | .
x x0 0
Пример.
Функция f (х) = sgn х имеет в точке х0 = 0 правый и левый пределы.
lim sign x 1; lim sign x 1.
x x0 0
Теорема.
x x0 0
Функция f (х) имеет в точке х0 предел тогда и только тогда, когда
в этой точке существуют как правый, так и левый пределы, и они
равны.

16.

Определение.
Число А называется пределом функции у = f (х) при х стремящемся к бесконечности ( х → ), если для любого ε > 0
найдется число S > 0, зависящее от ε, что для всех х, т.ч. | х | > S,
будет верно неравенство | f(x) – A | < ε:
A lim f ( x) 0 S ( ) 0 x :| x | S | f ( x) A | .
x
Пример.
Функция f (x) = 1/x имеет предел при x → равный нулю.
Геометрический смысл предела
Определение.
Число А называется пределом функции у = f (х) при х → +
( х → - ), если для любого ε > 0 найдется число S > 0, зависящее
от ε, что для всех х > S ( х < - S ), будет верно неравенство
| f(x) – A | < ε.

17.

Свойства бесконечно малых величин
Определение.
Если α(х) и β(х) бесконечно малые величины при х → х0 или
Функция α(х) называется бесконечно малой величиной при
хх →
малыми величинами:
→
х0, то
(х будут
→ ),бесконечно
если ее предел равен нулю:
1. α(х) ± β(х); 2. с∙α(х), с – постоянная; 3. α(х)∙β(х);
lim
( x)∙α
) (х0), f(х ) – ограниченная
0 ( ) 0 функция;
x x0 :| x x0 | | ( x) | ;
4.
f
(
х
x x0
lim
f (0x) S0( . ) 0 x :| x | S | ( x) | .
5. α((хx)) / f(0х),
lim
x x ( )
x
0
Сравнение порядков бесконечно малых.
Теорема.
Если α(х) и β(х) бесконечно малые величины при х → х0 или
х →Функция
, и lim f (х()x)имеет
/ ( x) kпри
, тох → х0 (х → ) предел, равный А,
x x0 ( )
тогда и только тогда, когда ее можно представить в виде
- при k = 0 бесконечно малая α(х) называется бесконечно малой
суммы этого числа А и бесконечно малой величины α(х) при
более высокого порядка малости, чем β(х);
х → х0 (х → ):
- при k = – более низкого порядка малости, чем β(х);
- при
А
– одного
lim 0 <f (kx<)
f ( xпорядка
) А малости;
( x), где lim ( x) 0.
x0 ( )k = 1 бесконечно малые α(х) и β(х) называются
x x0 ( )
-x при
эквивалентными, например, при х → 0 sin x х; In (1 + х) х; е х 1 + х.

18.

Определение.
Функция f(х) называется бесконечно большой величиной при
х → х0 ( х → ), если
M 0 (M ) 0 x x0 :| x x0 | | f ( x) | M ;
M 0 S (M ) 0 x :| x | S | f ( x) | M .
Свойства бесконечно больших величин
Замечание.
Бесконечно
большая величина
функция
Если f(х) бесконечно
большая есть
величина
принеограниченная
х → х0 ( х → ),
при
х → бесконечно
х0 (х → ), большими
однако неограниченная
то будут
величинами: функция не обязательно
большой
величиной.
1. f(является
х) ± φ(х), бесконечно
φ(х) – ограниченная
функция;
Пример.
2. f(х)∙φ(х), lim ( x) 0 ;
x x ( )
Теорема.
Функция y = x∙sin
x является неограниченной, но не бесконеч3. f(х)функция
/ φ(х), φα((хх))––имеет
предел.малая величина при х → х0
бесконечно
но Если
большой.
(х → ), то функция f(х) =1/α(х) является бесконечно большой, и
обратно, если f(х) – бесконечно большая функция при х → х0 (х
→ ), то α(х) = 1/ f(х) является бесконечно малой величиной.
0

19.

Основные теоремы о пределах
1. Если предел существует, то он единственный.
2. Функция, имеющая предел в точке, ограничена в некоторой
окрестности этой точки.
3. Если x f ( x) c x0 ( x ) lim f ( x) c.
4.
5.
6.
lim [ f ( x)] lim f ( x).
x x0 ( )
x x0 ( )
Однородность
x x0 ( )
lim [ f ( x) g ( x) ] lim
x x0 ( )
x x0 ( )
lim [ f ( x) g ( x)] lim
x x0 ( )
x x0 ( )
f ( x) lim g ( x).
x x0 ( )
Аддитивность
f ( x) lim g ( x).
x x0 ( )
f ( x)
f ( x) x lim
x0 ( )
, если lim g ( x) 0.
7. lim
x x0 ( ) g ( x )
x x0 ( )
g ( x)
x lim
x ( )
0
8. Если lim f (u) A и lim g ( x) u0 , lim f [ g ( x)] A.
u u0
x x0
x x0
9. Если x O( x0 , ) ( x ) f ( x) g ( x) lim
x x0 ( )
f ( x) lim g ( x).
x x0 ( )

20.

Замечание.
В теоремах о пределах предполагалось существование
пределов функций f(х) и g(х), из чего следует заключение о
пределах суммы, произведения частного и т.д.
Обратного может и не быть.
Примеры. lim [ tg x ctg x] lim 1 1, но lim tg x не существует.
x
2
x
2
x
2
sin x
Первый замечательный предел: lim
1.
x 0
x
x
1
Второй замечательный предел (число е): lim 1 e.
x
x
Признаки существования предела
1. Монотонная ограниченная в О(x0,ε) функция имеет предел в
точке x0.
2. lim ( x) lim ( x) A x O( x0 , ) ( x ) ( x) f ( x) ( x)
x x0 ( )
x x0 ( )
lim f ( x) A.
x x0 ( )

21.

ТРЕТИЙ ВОПРОС
Непрерывность функции

22.

Определение.
Определение.
Функция f(x) называется непрерывной в точке x0, если она
удовлетворяет
Функция f(x) следующим
называется условиям:
непрерывной в точке x0, если она
1) определена
в точке
x0 (существует
f(x0)); малому приращению
определена
в этой
точке
x0 и бесконечно
аргумента
соответствует
бесконечно
приращение функции:
2) имеет конечный
предел
при х → хмалое
0;
3) этот предел равен значению функции в точке х0:
lim y 0.
0 f (x
lim f ( xx )
lim
0 ). x).
x x0
x x0
Пример.
Определение.
(односторонняя непрерывность функции в точке)
Исследовать
в точке х0 = 0 заданных
Функция
f(x) непрерывность
называется непрерывной
в точкефункций.
x0 слева
(справа), если она удовлетворяет следующим условиям:
1) определена в точке x0 (существует f(x0));
2) имеет конечный предел при х → х0 – 0 ( х → х0 + 0);
3) этот предел равен значению функции в точке х0:
lim f ( x) f ( х0 ) ( lim f ( x) f ( х0 )).
x x0 0
x x0 0
Функция f(x) непрерывна в точке x0 тогда и только тогда,
когда
lim f ( x) lim f ( x) f ( х0 ).
x x0 0
x x0 0

23.

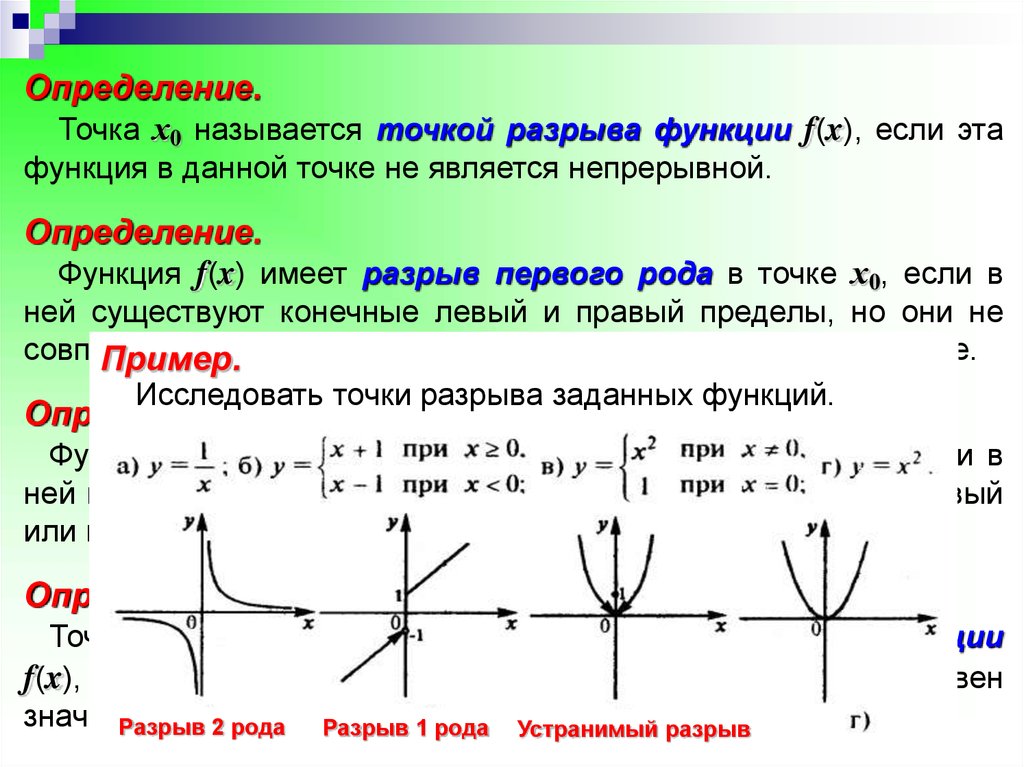
Определение.
Точка х0 называется точкой разрыва функции f(x), если эта
функция в данной точке не является непрерывной.
Определение.
Функция f(x) имеет разрыв первого рода в точке х0, если в
ней существуют конечные левый и правый пределы, но они не
совпадают
между собой или со значением функции в этой точке.
Пример.
Исследовать точки разрыва заданных функций.
Определение.
Функция f(x) имеет разрыв второго рода в точке х0, если в
ней не существует хотя бы один конечный односторонний (левый
или правый) предел.
Определение.
Точка х0 называется точкой устранимого разрыва функции
f(x), если предел функции при х → х0 существует, но не равен
значению
функции
этой точке.
Разрыв
2 рода вРазрыв
1 рода
Устранимый разрыв

24.

Свойства функций, непрерывных в точке
1. Если f (x) непрерывна точке х0, то > 0 такой, что f (x) ограничена в О( х0, ) этой точки.
2. Если f (x) непрерывна точке х0, то >0 такой, что х О( х0, )
этой точки f (x) имеет тот же знак, что и f (x0).
3. Если f (x) и g (x) непрерывны точке х0, то в ней непрерывны
f (x) ± g (x), f (x) · g (x), а также f (x) / g (x), если g (x) ≠ 0.
4. Пусть функция y = f (u) непрерывна в некоторой точке u0, а
функция u = g (x) – в точке х0, причем u0 = g (x0). Тогда сложная
функция y = f (g (x)) будет непрерывна в точке х0.
Следствие.
Если f (x) и g (x) удовлетворяют условиям свойства 4, то
lim f ( g ( x)) f ( lim g ( x)).
x x0
x x0

25.

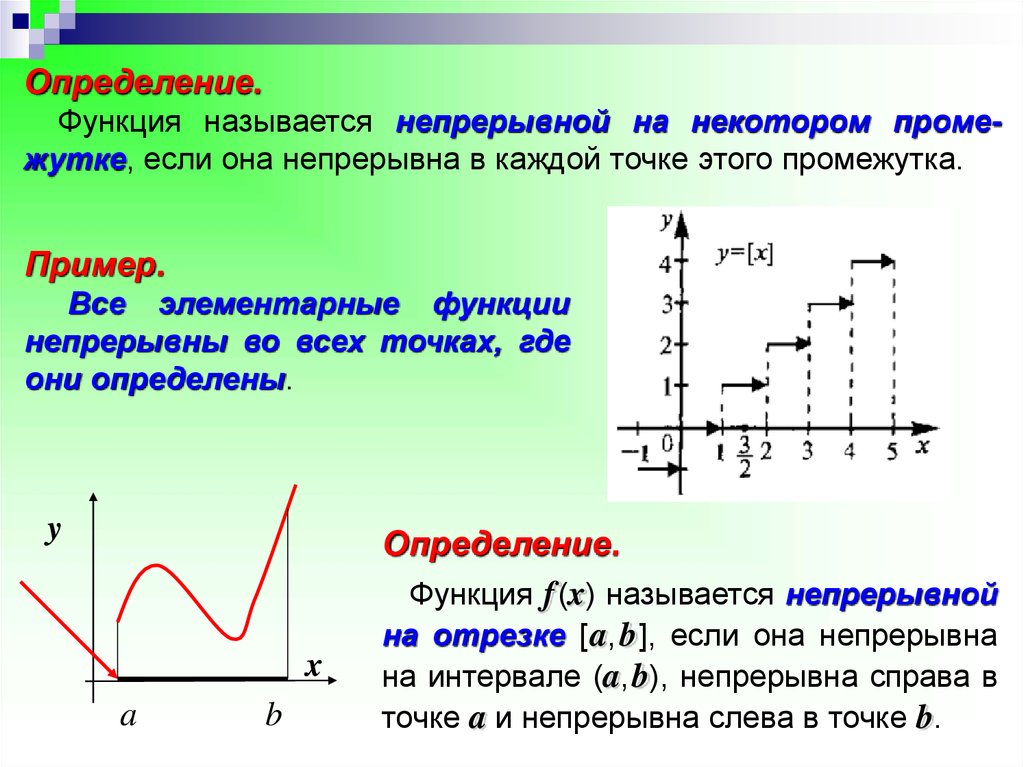
Определение.
Функция называется непрерывной на некотором промежутке, если она непрерывна в каждой точке этого промежутка.
Пример.
Все элементарные функции
непрерывны во всех точках, где
они определены.
y
x
a
b
Определение.
Функция f (x) называется непрерывной
на отрезке [ a, b ], если она непрерывна
на интервале (a, b), непрерывна справа в
точке a и непрерывна слева в точке b.

26.

Свойства функций, непрерывных на отрезке
3. Если
Если функция
f(x) непрерывна
на отрезке
, b] и принимает
на его
f(x) непрерывна
на[aотрезке
[a,b], то она:
концах значения разных знаков, то она равна нулю в некоторой
1. Ограничена на нем (1-я теорема Вейерштрасса)
точке интервала (a, b) (1-я теорема Больцано-Коши)
, b]
f (M
a) , m
f (b )x 0[a
(ma, b)f f( x( ) ) M0;;
2.
на нем свои
наибольшее
и наименьшее
4. Принимает
Если f(x) непрерывна
на отрезке
[a, b], то
она принимает на
значения
(
2-я
теорема
Вейерштрасса
)
нем любое значение между своими наибольшим и наименьшим значениями
теорема
xM , xm [a(2-я
, b]
x [a, b] Больцано-Коши)
f ( xm ) f ( x) f ( xM ).
y [ f ( xm ), f ( xM )] [a, b] f ( ) y.
y
M y
f(xM)
f(xM)
a xm y=f(ξ)0
b
x
a xm
x
0
xM b
ξ xM
f(xm))
m f(x
m
Бернард
Больцано
Карл
Вейерштрасс

27.

Благодарю за внимание,
лекция окончена!