Лекция 4 - Обобщенные позиционные задачи. Сечение гр. поверхности плоскостью ЧП (1)

1. ПОЗИЦИОННЫЕ ЗАДАЧИ

2.

ПОЗИЦИОННЫЕ ЗАДАЧИ
-
-
Задачи на определение взаимного положения геометрических образов:
Позиции (выше-ниже; левее-правее; дальше-ближе).
Принадлежность (точка принадлежит линии; точка и линия принадлежат
плоскости; точка и линия принадлежат поверхности).
Параллельность (прямые параллельны; прямая параллельна плоскости;
2 плоскости параллельны).
Пересечение (2 пересекающиеся прямые; прямая пересекается c плоскостью;
прямая пересекается c поверхностью; 2 плоскости пересекаются; Плоскость
пересекается c поверхностью) .
Пересечение ГО - определение общего элемента пересечения:
1 Основная позиционная задача – это определение точек пересечения прямой
с поверхностью (плоскостью).
2 Основная позиционная задача – определение линии пересечения двух
плоскостей, поверхности с плоскостью, двух поверхностей.

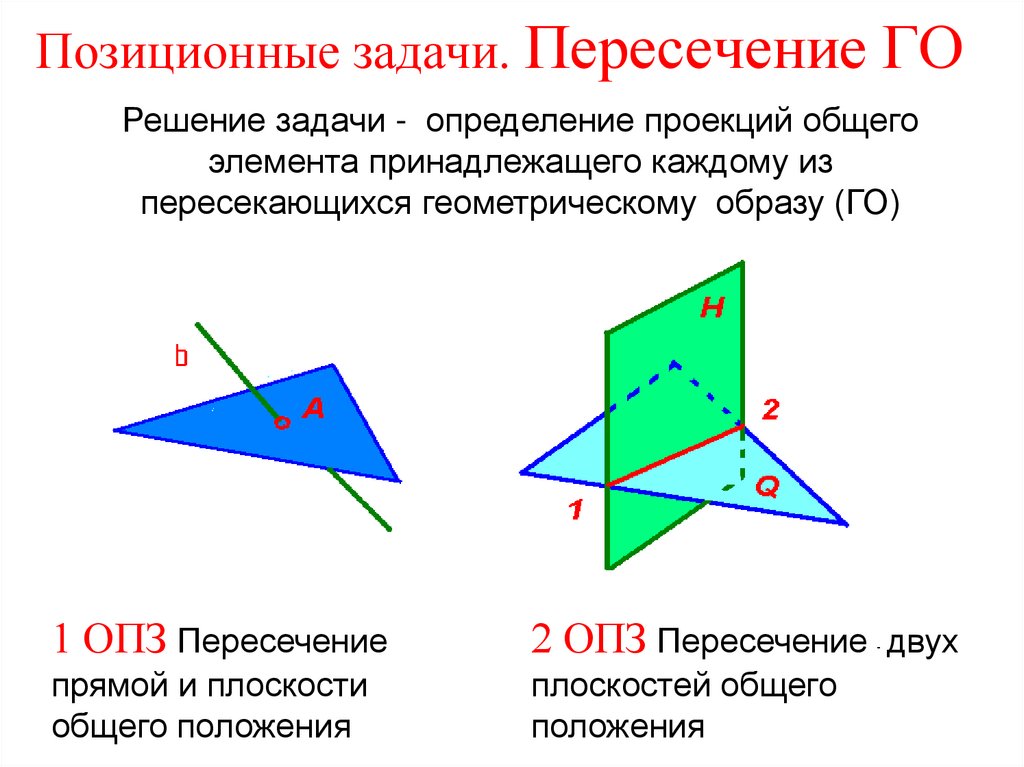
3. Позиционные задачи. Пересечение ГО

Решение задачи - определение проекций общего
элемента принадлежащего каждому из
пересекающихся геометрическому образу (ГО)
1 ОПЗ Пересечение
2 ОПЗ Пересечение двух
прямой и плоскости
общего положения
плоскостей общего
положения

4. 3типа задач на пересечение ГО

3 случая расположения пересекающихся
геометрических образов, относительно
плоскостей проекций, от которых зависит
алгоритм решения задачи:
1. оба образа являются проецирующими (┴∩┴);
2. один их них является проецирующим (┴∩┴);
3. оба геометрических образа – непроецирующие (┴∩┴).
1. Пересечение проецирующих
геометрических образов
Решение задач в этом случае основано на собирательном свойстве их
вырожденных проекций

5.

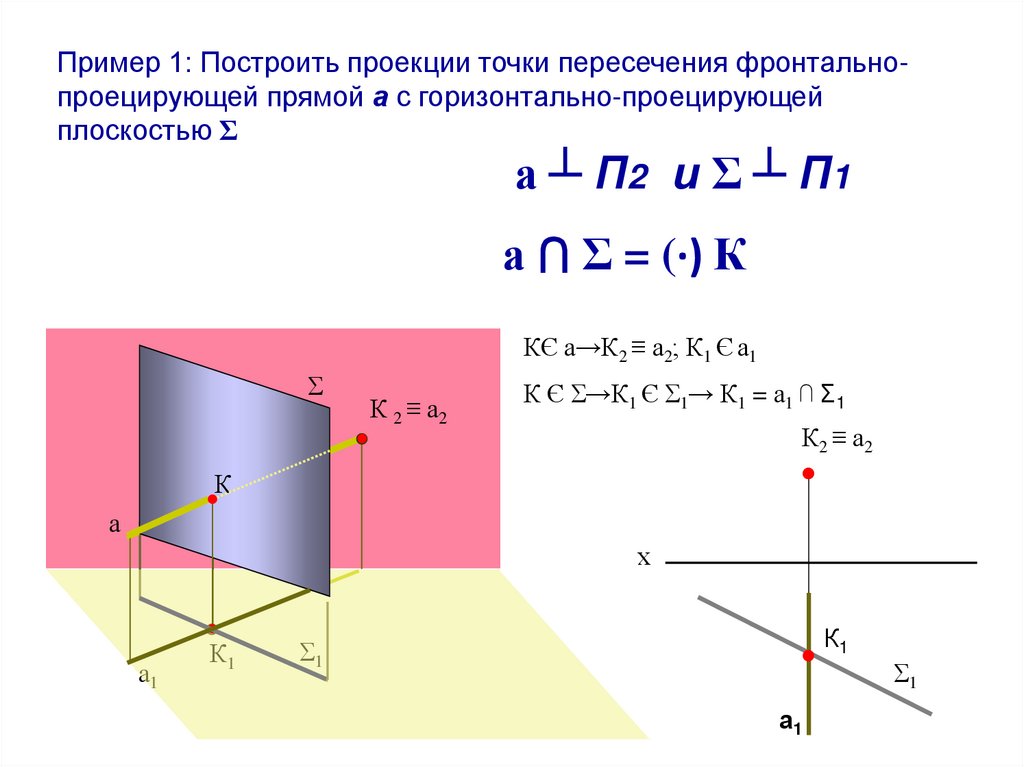
Пример 1: Построить проекции точки пересечения фронтальнопроецирующей прямой а с горизонтально-проецирующей
плоскостью Σ
а ┴ П2 и Σ ┴ П1
а ⋂ Σ = (·) К
КЄ а→К2 ≡ а2; К1 Є а1
Σ
К 2 ≡ а2
К Є Σ→К1 Є Σ1→ К1 = а1 ⋂ Σ1
К2 ≡ а2
КК
а
х
а1
К1
К1
Σ1
Σ1
а1

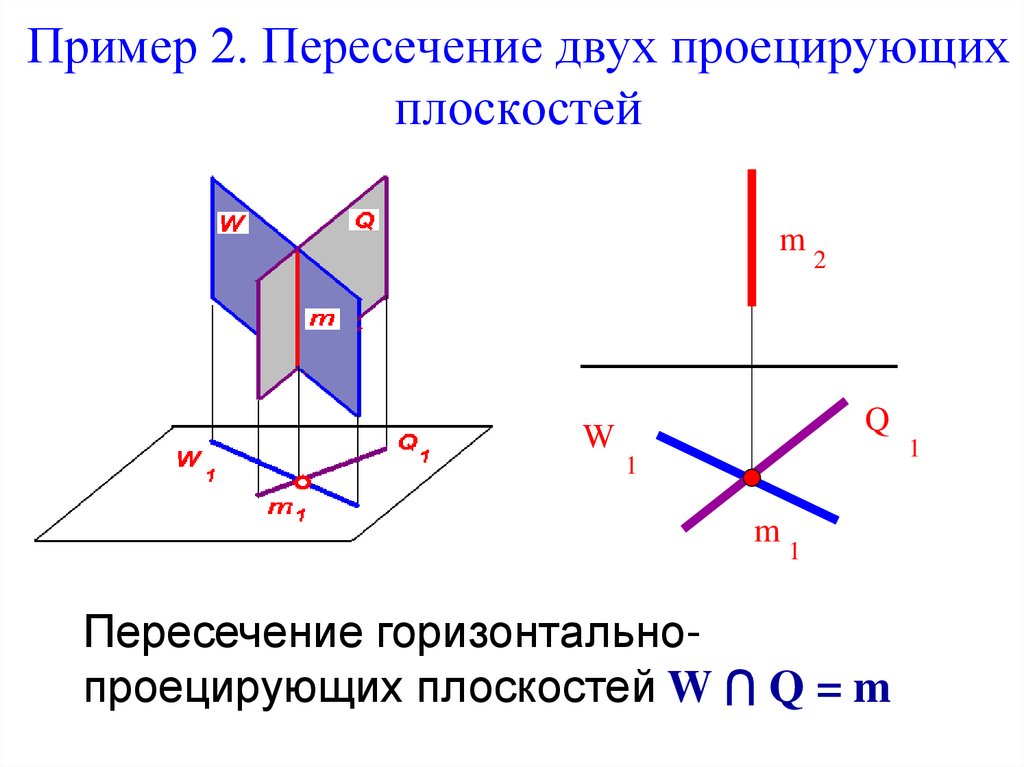
6. Пример 2. Пересечение двух проецирующих плоскостей

m
2
Q
W
1
1
m
1
Пересечение горизонтальнопроецирующих плоскостей W ⋂ Q = m

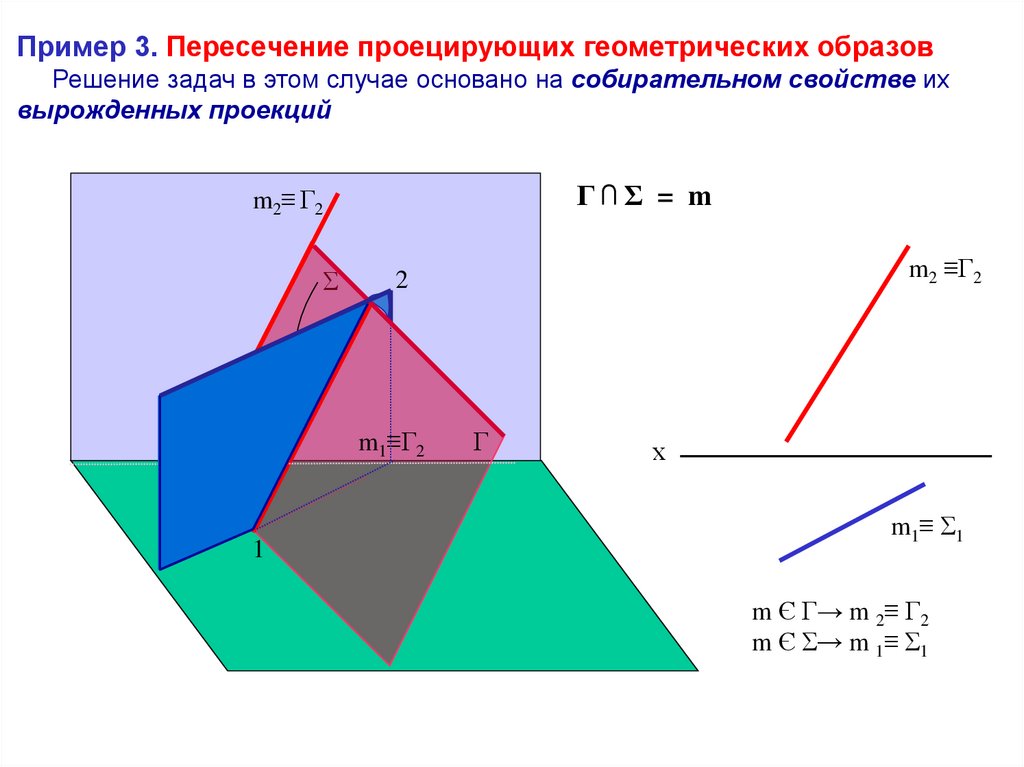
7.

Пример 3. Пересечение проецирующих геометрических образов
Решение задач в этом случае основано на собирательном свойстве их
вырожденных проекций
Г⋂Σ = m
m2≡ Г2
Σ
m2 ≡Г2
2
Σ
m
m1≡Г2
1
Г
х
m1≡ Σ1
m Є Г→ m 2≡ Г2
m Є Σ→ m 1≡ Σ1

8.

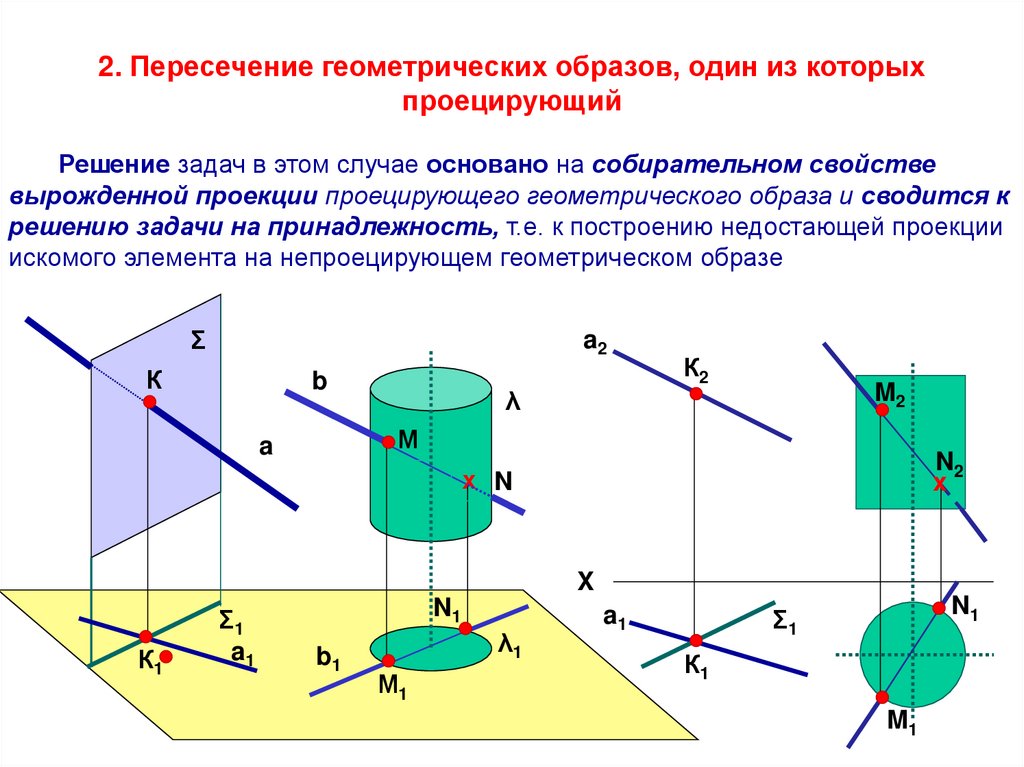
2. Пересечение геометрических образов, один из которых
проецирующий
Решение задач в этом случае основано на собирательном свойстве
вырожденной проекции проецирующего геометрического образа и сводится к
решению задачи на принадлежность, т.е. к построению недостающей проекции
искомого элемента на непроецирующем геометрическом образе
Σ
a2
К
b
λ
К2
M2
М
a
N2
x
х N
X
К1
Σ1
a1
N1
b1
λ1
М1
a1
N1
Σ1
К1
M1

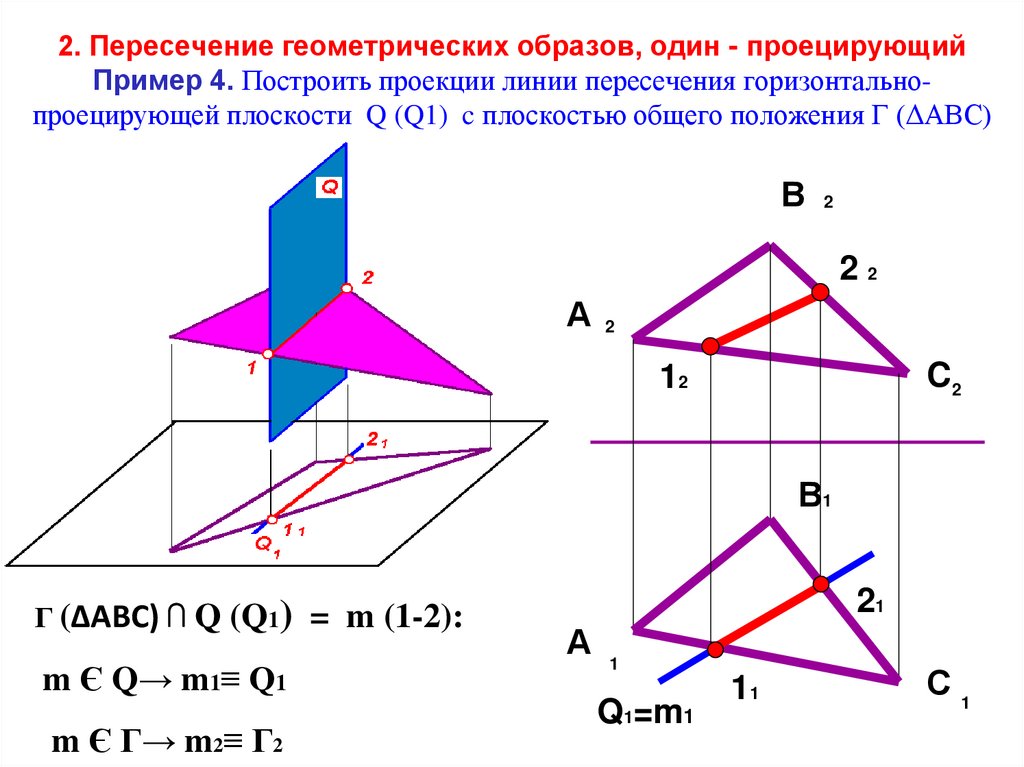
9. 2. Пересечение геометрических образов, один - проецирующий Пример 4. Построить проекции линии пересечения

горизонтальнопроецирующей плоскости Q (Q1) c плоскостью общего положения Г (ΔАВС)
В 2
22
А 2
C2
12
В1
Г (ΔАВС) ⋂ Q (Q1) = m (1-2):
m Є Q→ m1≡ Q1
m Є Г→ m2≡ Г2
21
А 1
Q1=m1
11
С1

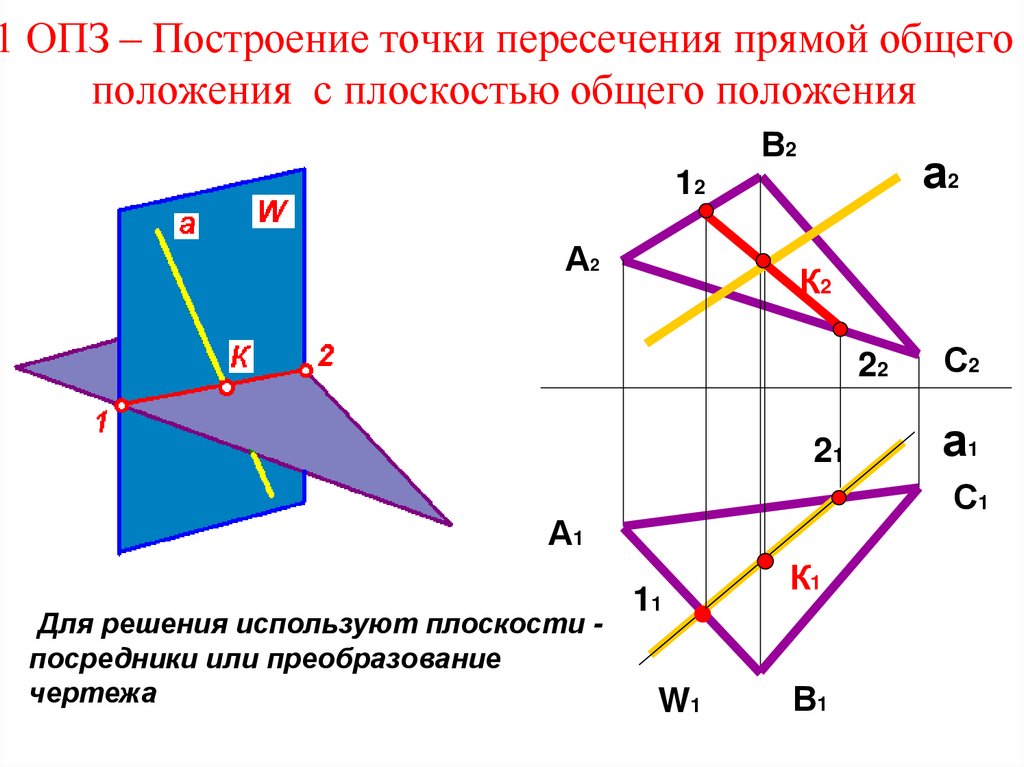
10. 1 ОПЗ – Построение точки пересечения прямой общего положения с плоскостью общего положения

В2
а2
12
А2
К2
22
21
а1
С1
А1
Для решения используют плоскости посредники или преобразование
чертежа
С2
11
W1
К1
В1

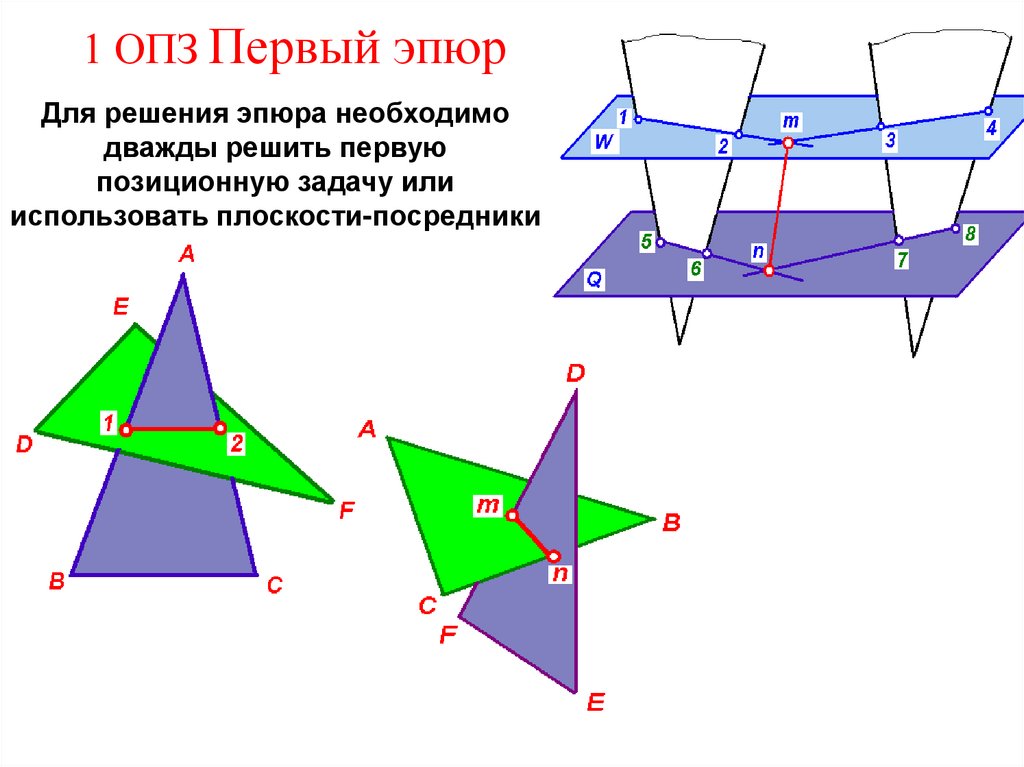
11. 1 ОПЗ Первый эпюр

Для решения эпюра необходимо
дважды решить первую
позиционную задачу или
использовать плоскости-посредники

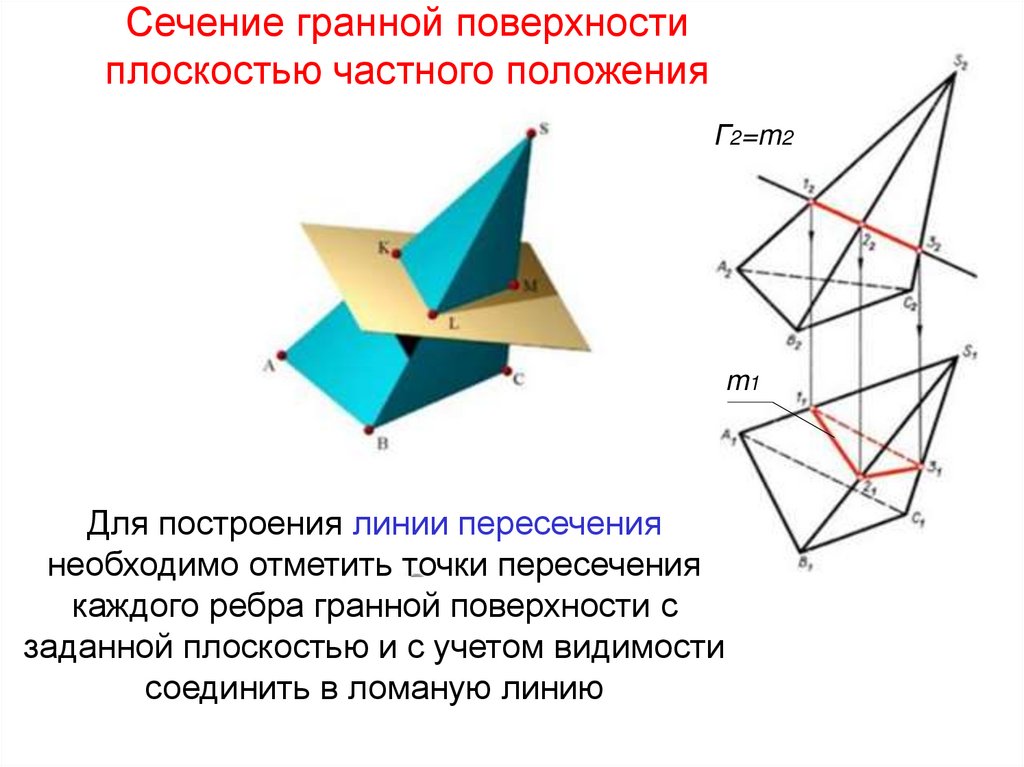
12. Сечение гранной поверхности плоскостью частного положения

Г2=m2
m1
Для построения линии пересечения
необходимо отметить точки пересечения
каждого ребра гранной поверхности с
заданной плоскостью и с учетом видимости
соединить в ломаную линию

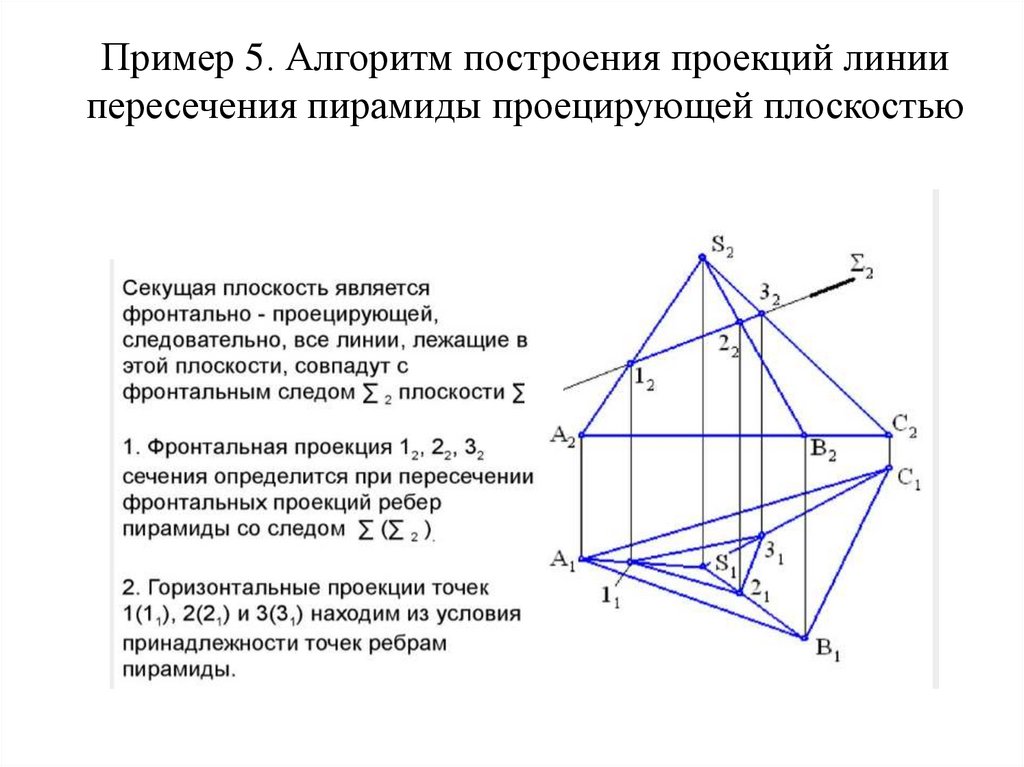
13. Пример 5. Алгоритм построения проекций линии пересечения пирамиды проецирующей плоскостью

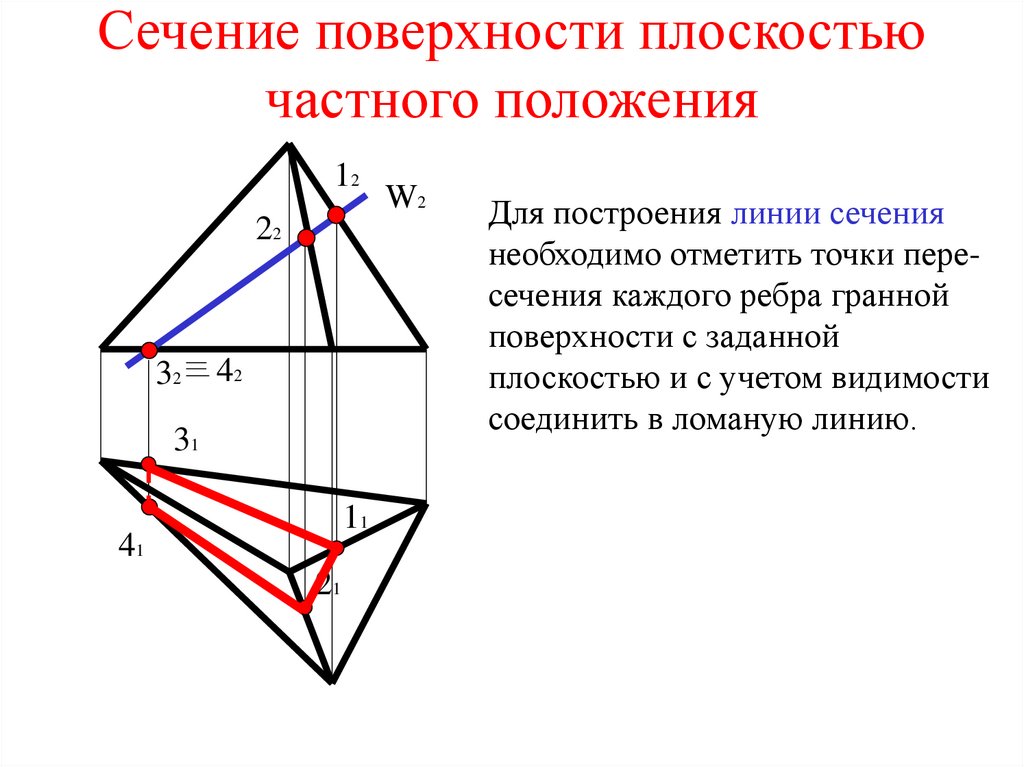
14. Сечение поверхности плоскостью частного положения

12
22
32
42
31
11
41
21
W2
Для построения линии сечения
необходимо отметить точки пересечения каждого ребра гранной
поверхности с заданной
плоскостью и с учетом видимости
соединить в ломаную линию.

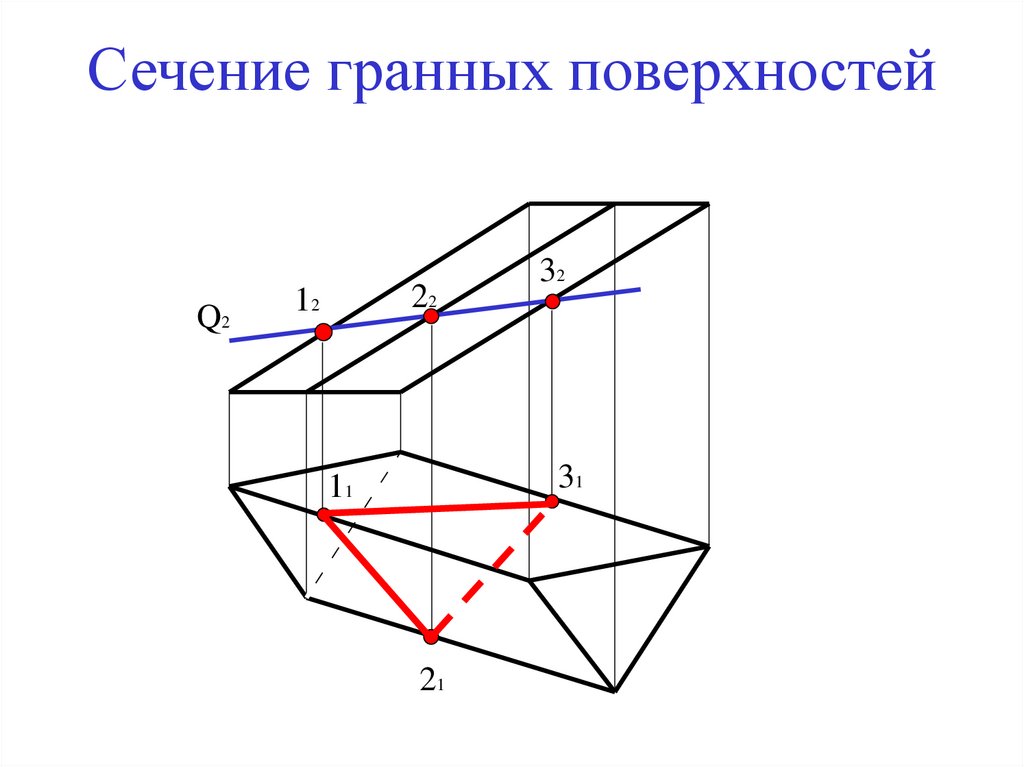
15. Сечение гранных поверхностей

Q2
22
12
32
31
11
21

16. Сечение призмы проецирующей плоскостью

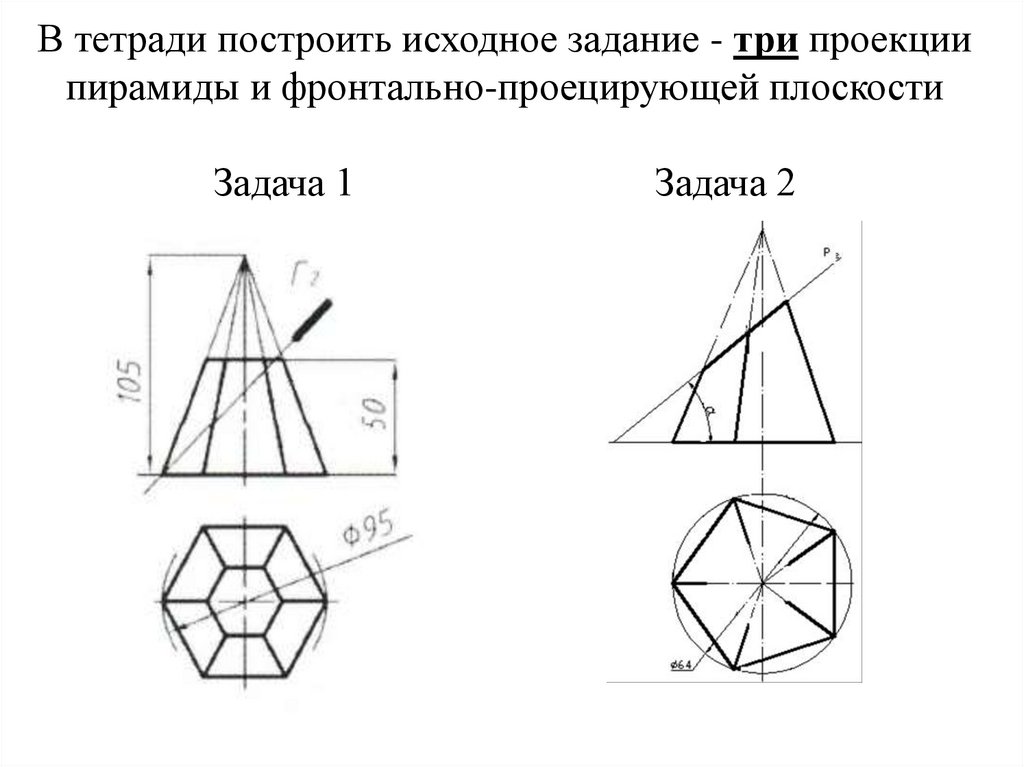
17. В тетради построить исходное задание - три проекции пирамиды и фронтально-проецирующей плоскости Задача 1 Задача 2

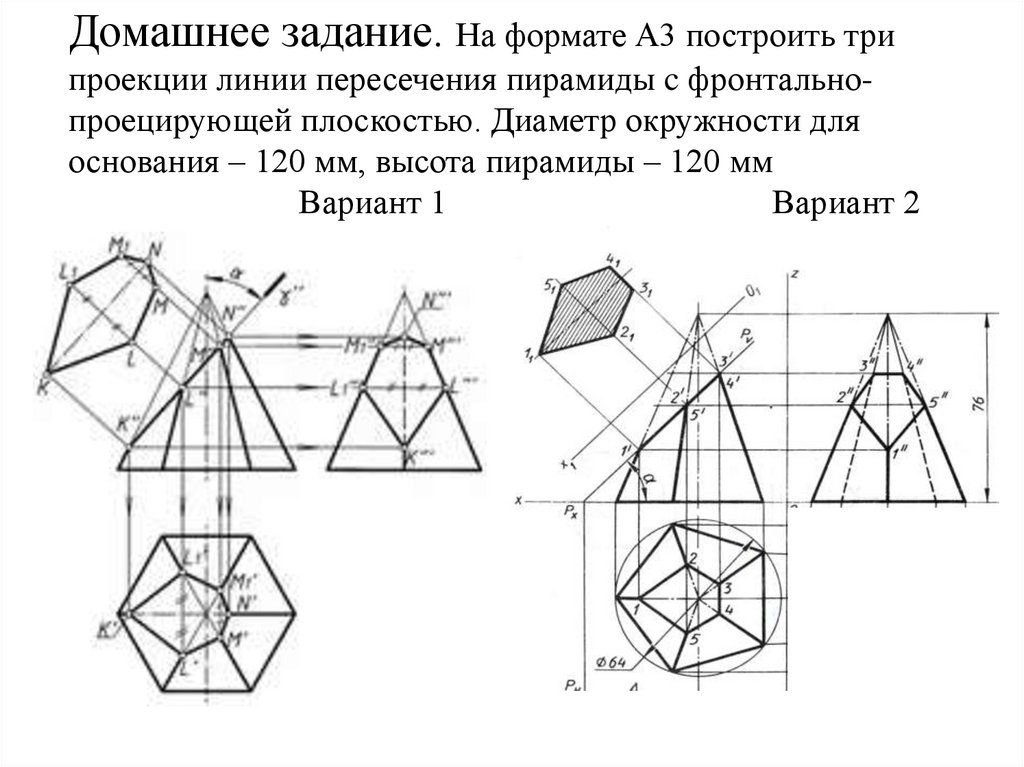
18. Домашнее задание. На формате А3 построить три проекции линии пересечения пирамиды c фронтально-проецирующей плоскостью. Диаметр

Домашнее задание. На формате А3 построить три
проекции линии пересечения пирамиды c фронтальнопроецирующей плоскостью. Диаметр окружности для
основания – 120 мм, высота пирамиды – 120 мм
Вариант 1
Вариант 2