Проецирование плоскости

1. Проецирование плоскости

ЛЕКЦИЯ №3
ПРОЕЦИРОВАНИЕ ПЛОСКОСТИ
Разработал: канд.пед.наук, доцент каф.НГГ
Брыкова Людмила Валерьевна

2. ПЛАН ЛЕКЦИИ:

1)
2)
3)
4)
5)
6)
7)
8)
Задание и изображение плоскости.
Следы плоскости.
Положение плоскости относительно плоскостей проекций.
Точка и прямая, расположенные в плоскости.
Главные линии плоскости.
Определение углов наклона плоскости к плоскостям
проекций.
Взаимное положение прямой и плоскости.
Взаимное расположение двух плоскостей.

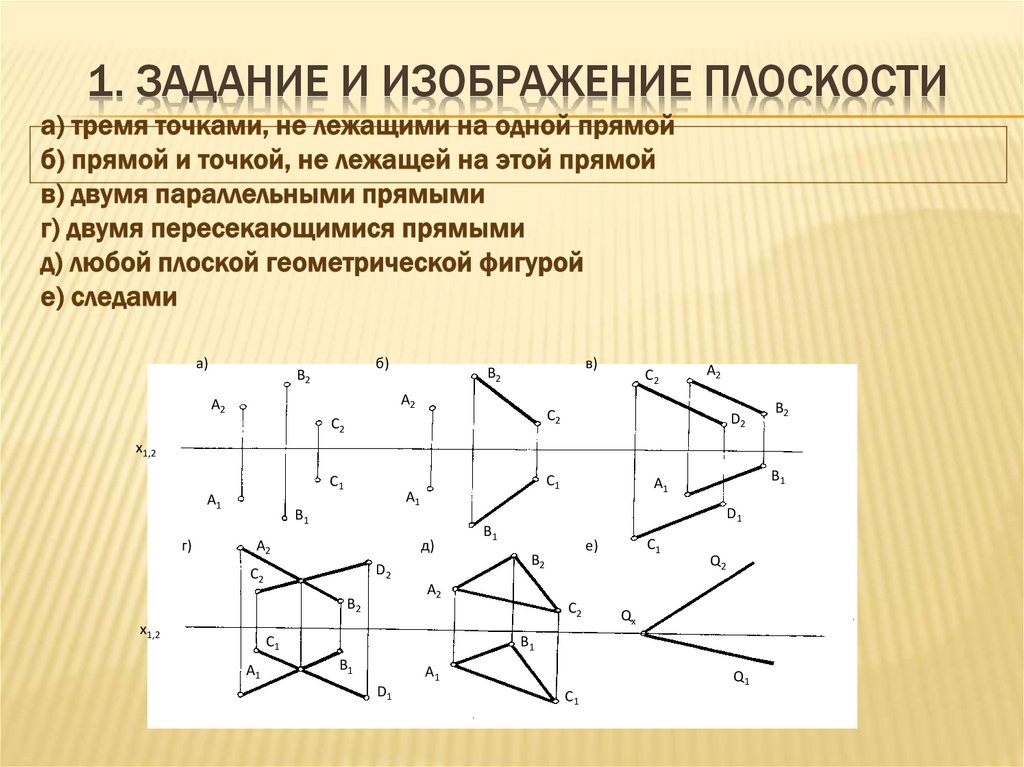
3. 1. Задание и изображение плоскости а) тремя точками, не лежащими на одной прямой б) прямой и точкой, не лежащей на этой прямой

1. ЗАДАНИЕ И ИЗОБРАЖЕНИЕ ПЛОСКОСТИ
a)
б)
B2
в)
B2
A2
A2
C2
A2
C2
C2
D2
B2
x1,2
C1
A1
г)
A1
B1
A2
д)
D2
C2
D1
B1
C1
е)
B2
C2
C1
A1
B1
A1
Q2
A2
B2
x1,2
C1
Qx
B1
B1
A1
D1
Q1
C1

4. 2. Следы плоскости Следом называют линию пересечения данной плоскости с плоскостью проекций (проекции следов, совпадающие с

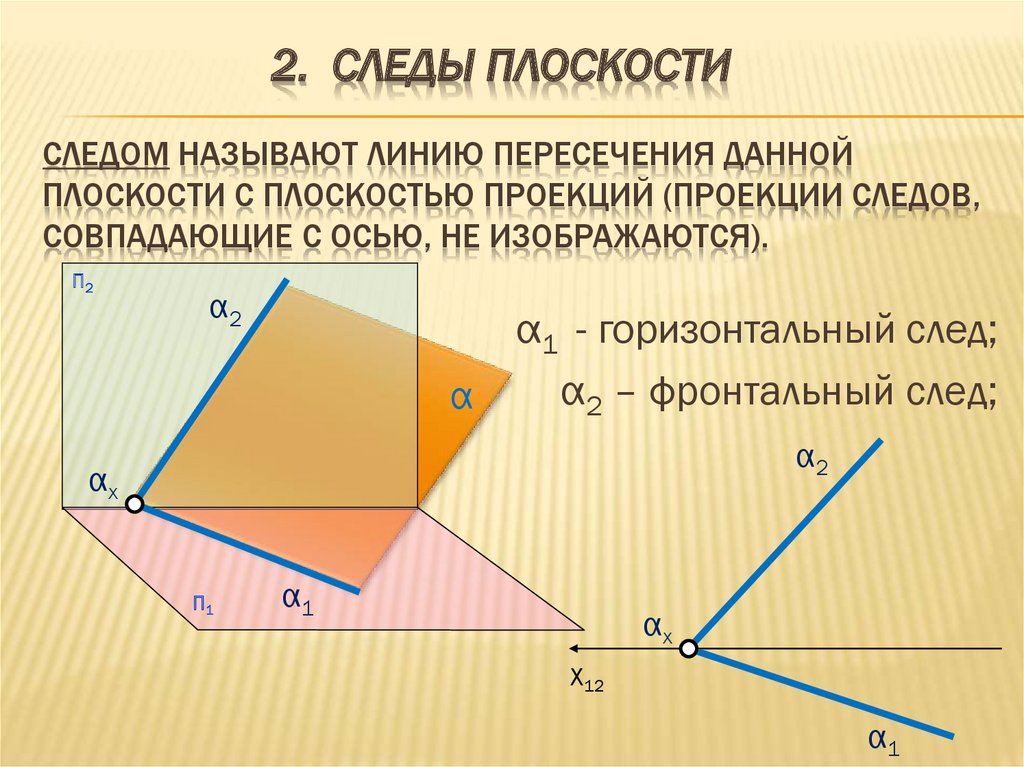
2. СЛЕДЫ ПЛОСКОСТИ
СЛЕДОМ НАЗЫВАЮТ ЛИНИЮ ПЕРЕСЕЧЕНИЯ ДАННОЙ
ПЛОСКОСТИ С ПЛОСКОСТЬЮ ПРОЕКЦИЙ (ПРОЕКЦИИ СЛЕДОВ,
СОВПАДАЮЩИЕ С ОСЬЮ, НЕ ИЗОБРАЖАЮТСЯ).
П2
α2
α
α1 - горизонтальный след;
α2 – фронтальный след;
α2
αx
П1
α1
αx
Х12
α1

5. 3. Положение плоскости относительно плоскостей проекций

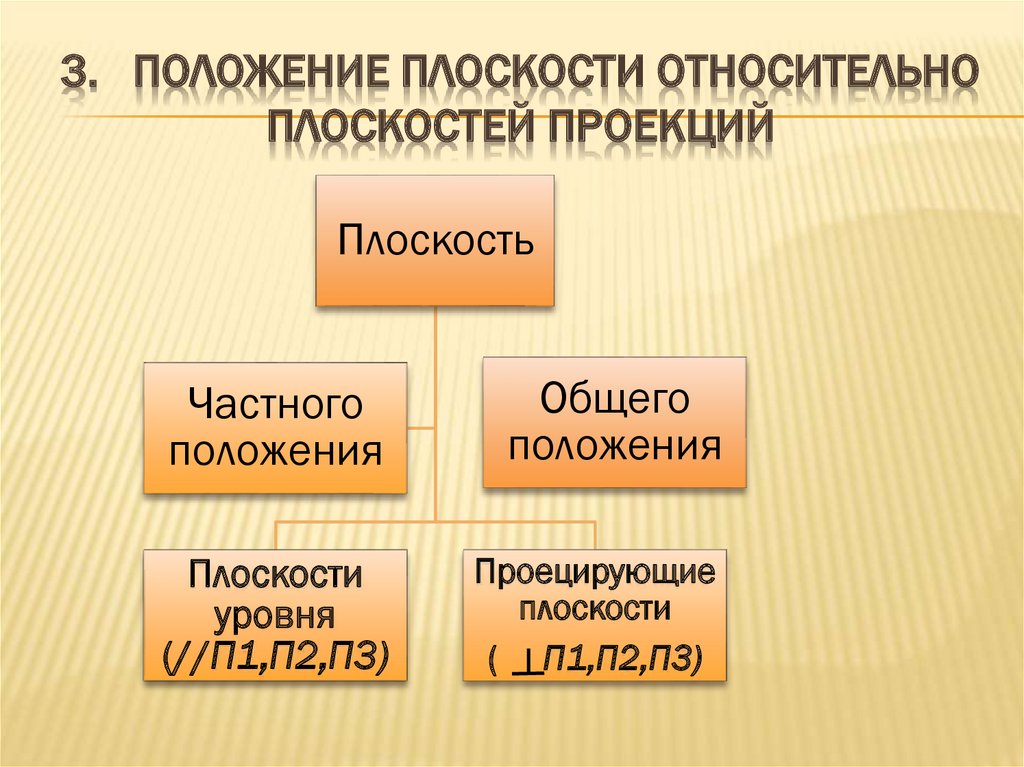
3. ПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО
ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Плоскость
Частного
положения
Общего
положения
Плоскости
уровня
(//П1,П2,П3)
Проецирующие
плоскости
( П1,П2,П3)

6. Плоскость  к одной из плоскостей проекций, называется проецирующей.

ПЛОСКОСТЬ К ОДНОЙ ИЗ ПЛОСКОСТЕЙ ПРОЕКЦИЙ,
НАЗЫВАЕТСЯ ПРОЕЦИРУЮЩЕЙ.
a)
а).плоскость,
перпендикулярная
горизонтальной плоскости П1,
называется горизонтально
проецирующей.
б) плоскость,
перпендикулярная
фронтальной плоскости
проекций П2, называется
фронтально проецирующей.
в) плоскость,
перпендикулярная
профильной плоскости
проекций П3, называется
профильно проецирующей.
б)
в)
B2
C2
B2
B3
B2
A2
C2
C2
A2
A1
А3
В1
C1
B1
C1
B1
А1
С3
A2
A1
C1

7. Плоскость, //какой-либо плоскости проекции, называют плоскостью уровня.

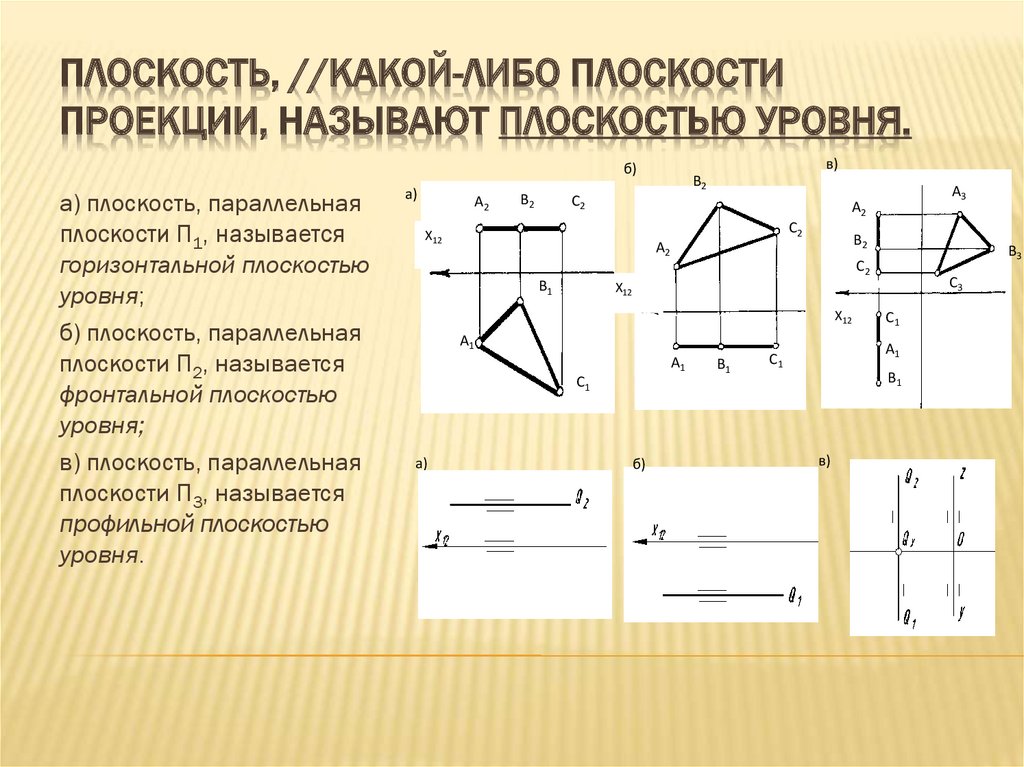
ПЛОСКОСТЬ, //КАКОЙ-ЛИБО ПЛОСКОСТИ
ПРОЕКЦИИ, НАЗЫВАЮТ ПЛОСКОСТЬЮ УРОВНЯ.
в)
б)
а) плоскость, параллельная
плоскости П1, называется
горизонтальной плоскостью
уровня;
б) плоскость, параллельная
плоскости П2, называется
фронтальной плоскостью
уровня;
в) плоскость, параллельная
плоскости П3, называется
профильной плоскостью
уровня.
a)
A2
B2
B2
C2
A3
A2
C2
X12
B2
A2
B3
C2
B1
X12
A1
A1
C1
a)
C3
X12
б)
B1
C1
A1
C1
B1
в)

8. 4. Точка и прямая, расположенные в плоскости

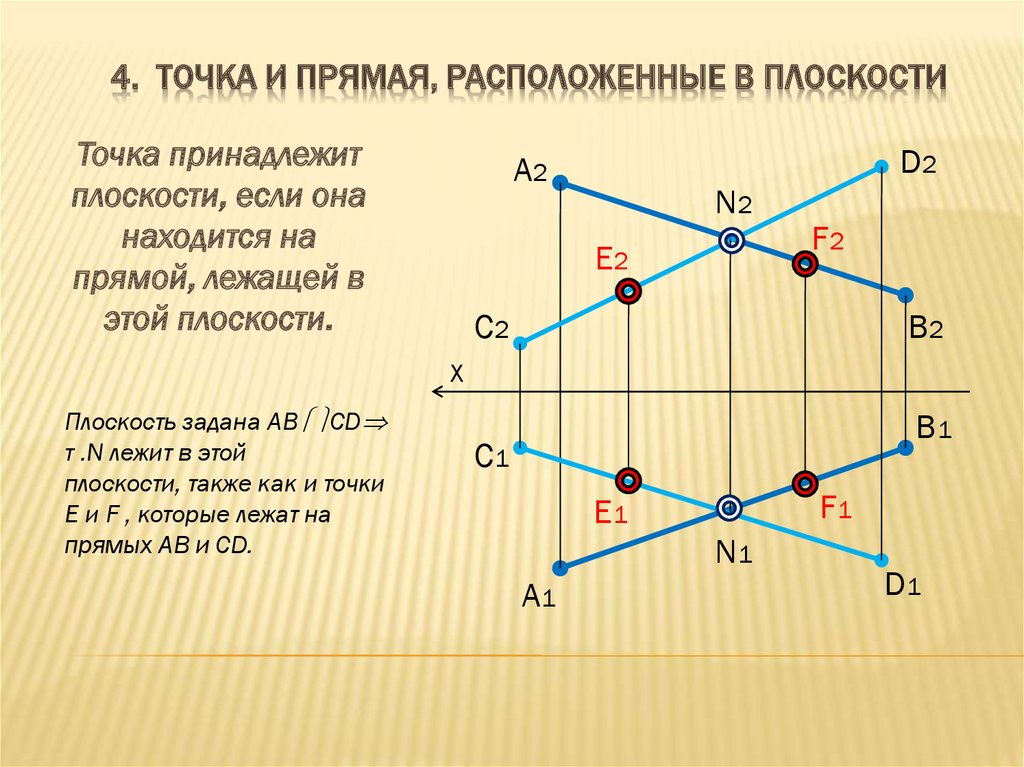
4. ТОЧКА И ПРЯМАЯ, РАСПОЛОЖЕННЫЕ В ПЛОСКОСТИ
Точка принадлежит
плоскости, если она
находится на
прямой, лежащей в
этой плоскости.
D2
A2
N2
E2
F2
C2
B2
X
Плоскость задана AB CD
т .N лежит в этой
плоскости, также как и точки
E и F , которые лежат на
прямых AB и CD.
B1
C1
F1
E1
N1
A1
D1

9. 4. Точка и прямая, расположенные в плоскости

4. ТОЧКА И ПРЯМАЯ, РАСПОЛОЖЕННЫЕ В ПЛОСКОСТИ
Прямая принадлежит
плоскости, если она
проходит:
а2
М2
В2
А2
b2
1) через две точки,
принадлежащие этой
плоскости;
2) через точку, принадлежащую
данной плоскости и
параллельно любой прямой
этой плоскости.
С2
А1
С1
а1
b1
М1
В1

10.

B2
A2
N2
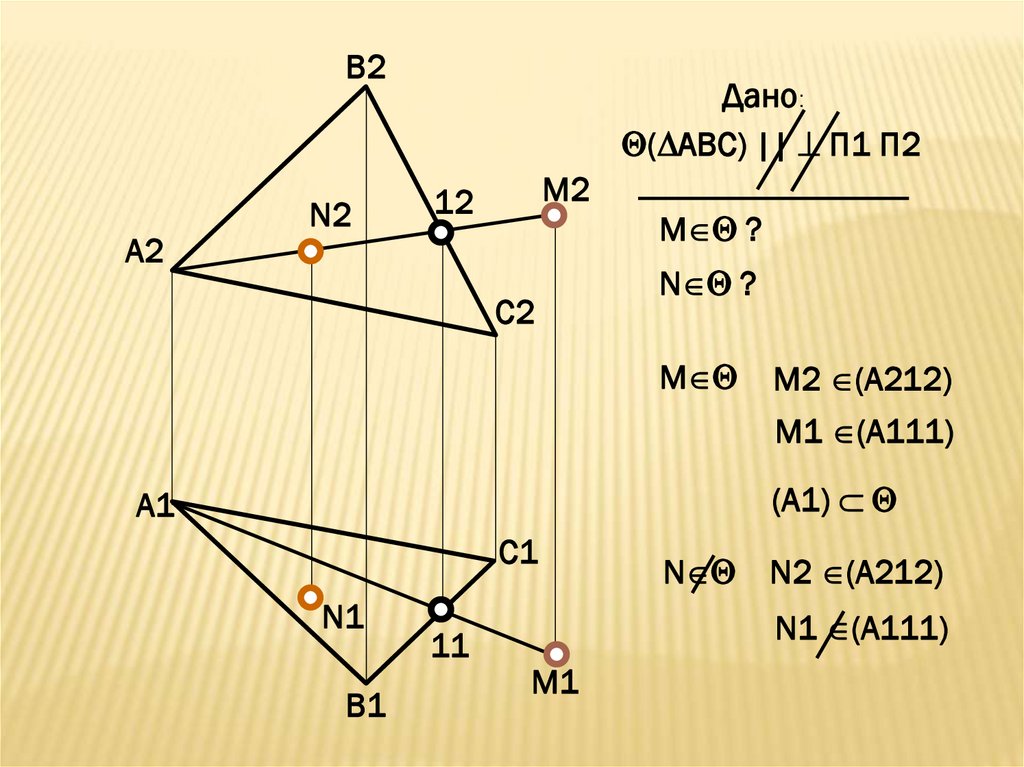
Дано:
( АВС) || П1 П2
М2
12
М ?
C2
N ?
М
М2 (A212)
М1 (A111)
(A1)
A1
C1
N1
B1
11
N N2 (A212)
N1 (A111)
М1

11.

B2
12
A2
C2
22
D2
E2
B1
11
A1
21
E1
C1
D1
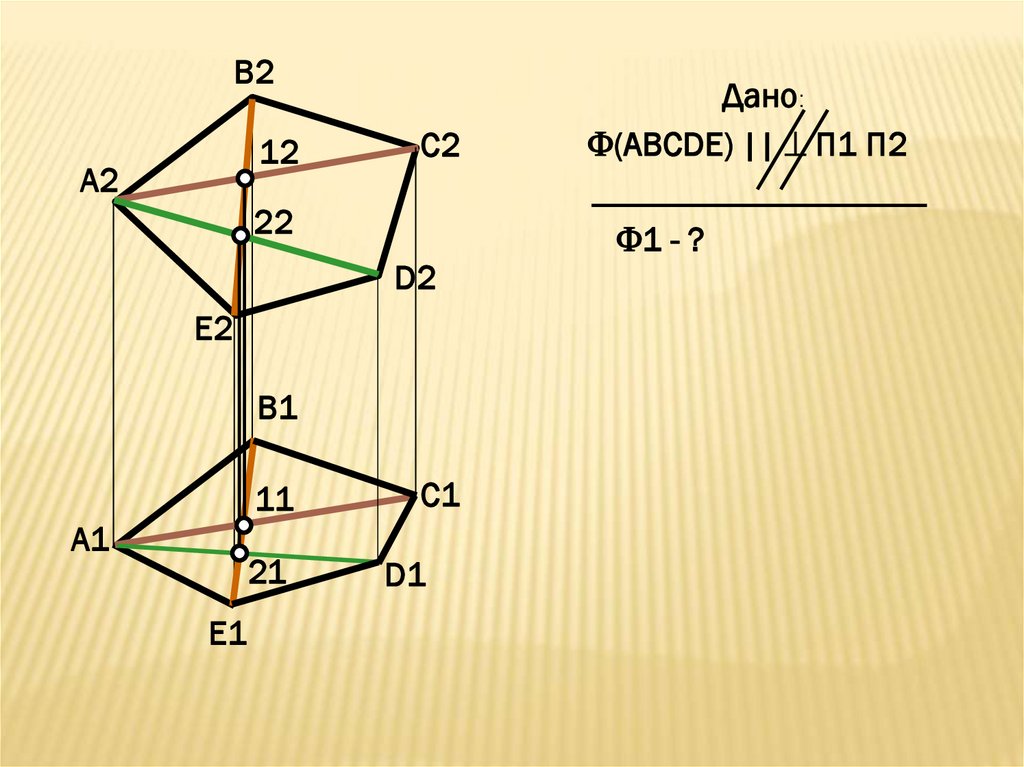
Дано:
(АВСDE) || П1 П2
1 - ?

12. 5. Главные линии плоскости

5. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
Горизонталь плоскости –
прямая, принадлежащая
плоскости и параллельная
горизонтальной плоскости
h АВС, h , h ‖ П1.
Фронталь плоскости –
прямая, принадлежащая
плоскости и параллельная
фронтальной плоскости
проекций
АВС, , ‖ П2.

13. 5. Главные линии плоскости

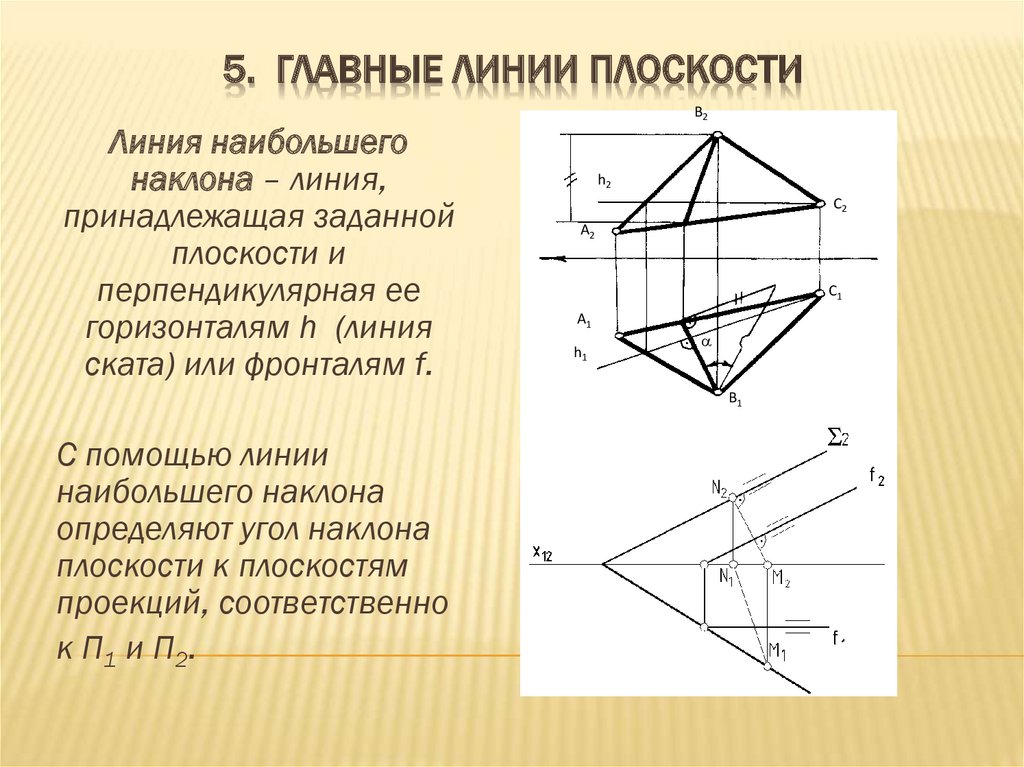
5. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
Линия наибольшего
наклона – линия,
принадлежащая заданной
плоскости и
перпендикулярная ее
горизонталям h (линия
ската) или фронталям f.
B2
h2
C2
A2
C1
A1
h1
B1
С помощью линии
наибольшего наклона
определяют угол наклона
плоскости к плоскостям
проекций, соответственно
к П1 и П2.

14. Взаимное положение прямой и плоскости: ПАРАЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ:
ПАРАЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
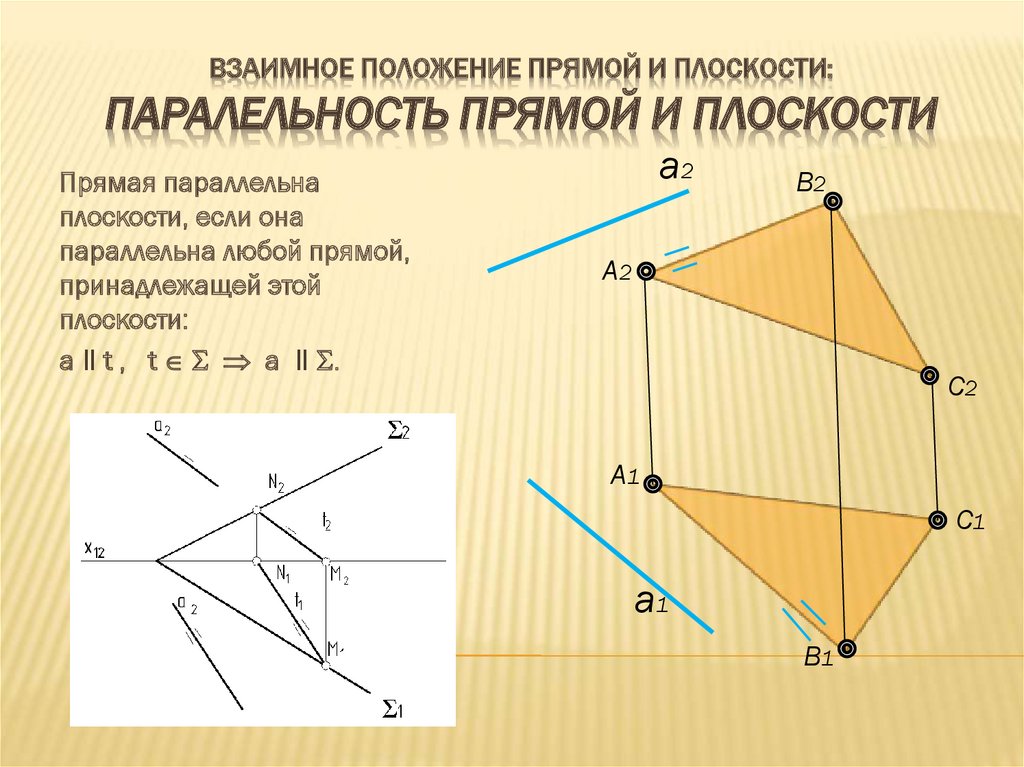
Прямая параллельна
плоскости, если она
параллельна любой прямой,
принадлежащей этой
плоскости:
а ‖ t , t a ‖ .
а2
В2
А2
С2
А1
С1
а1
В1

15. Взаимное положение прямой и плоскости: ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Прямая перпендикулярна плоскости , если она
перпендикулярна двумя пересекающимся прямым,
лежащим в этой плоскости.
В качестве пересекающихся прямых на
плоскости выбирают горизонталь h и
фронталь .
В этом случае можно воспользоваться
свойствами проекций прямого угла:
a h, a , h Ⴖ ,
h , а .
При этом прямые углы между прямой а и
прямыми h и на соответствующие
плоскости проекций спроецируются в
натуральную величину:
а 1 h 1, а 2 2 .
Если плоскость задана
следами, то горизонталью и
фронталью плоскости
являются ее
пересекающиеся следы
а1 1, а2 2,
1 Ⴖ 2 а .

16.

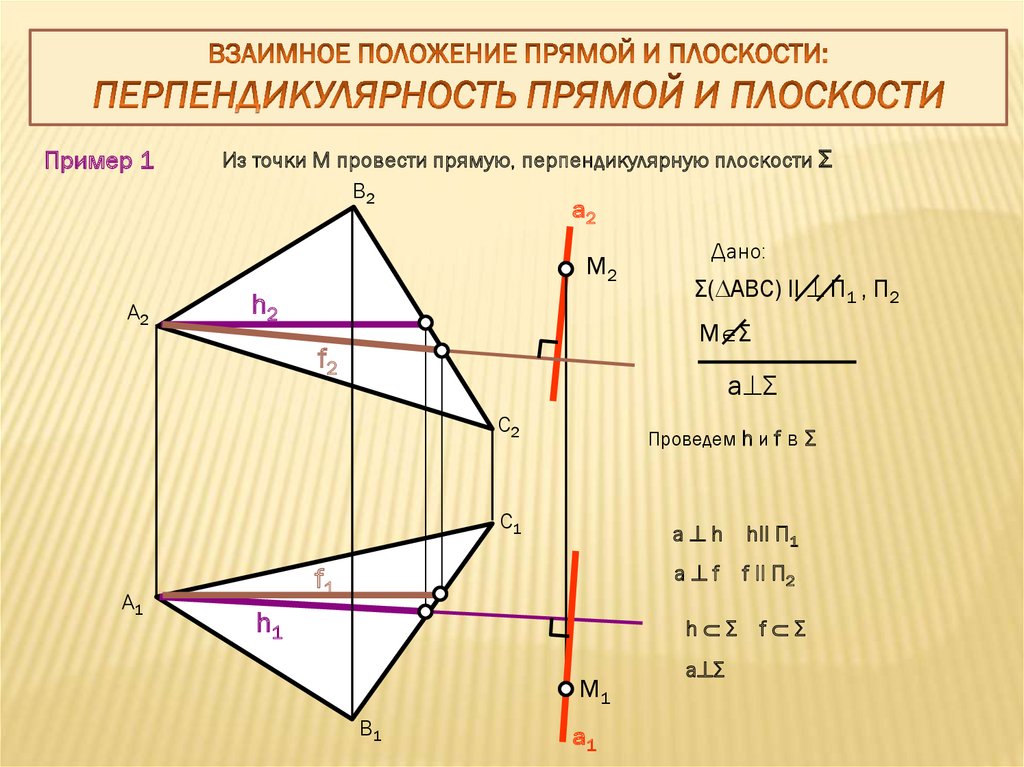
Пример 1
Из точки М провести прямую, перпендикулярную плоскости Σ
B2
a2
M2
A2
h2
Σ( АВС) ll П1 , П2
M Σ
f2
a Σ
C2
Проведем h и f в Σ
C1
A1
Дано:
a h hll П1
a f
f1
h1
h Σ
M1
B1
a1
a Σ
f ll П2
f Σ

17. Взаимное положение прямой и плоскости: ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ:
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
B2
B1
K1
фронтальная проекция точки пересечения прямой АВ с плоскостью
(CDE) и Q определяется: К2 = А2В2 Ⴖ С2D2E2, а К1 А1В1;
К2 = А2В2 Ⴖ Q 2, а К1 А1В 1;

18. Взаимное положение прямой и плоскости: ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ общего положения

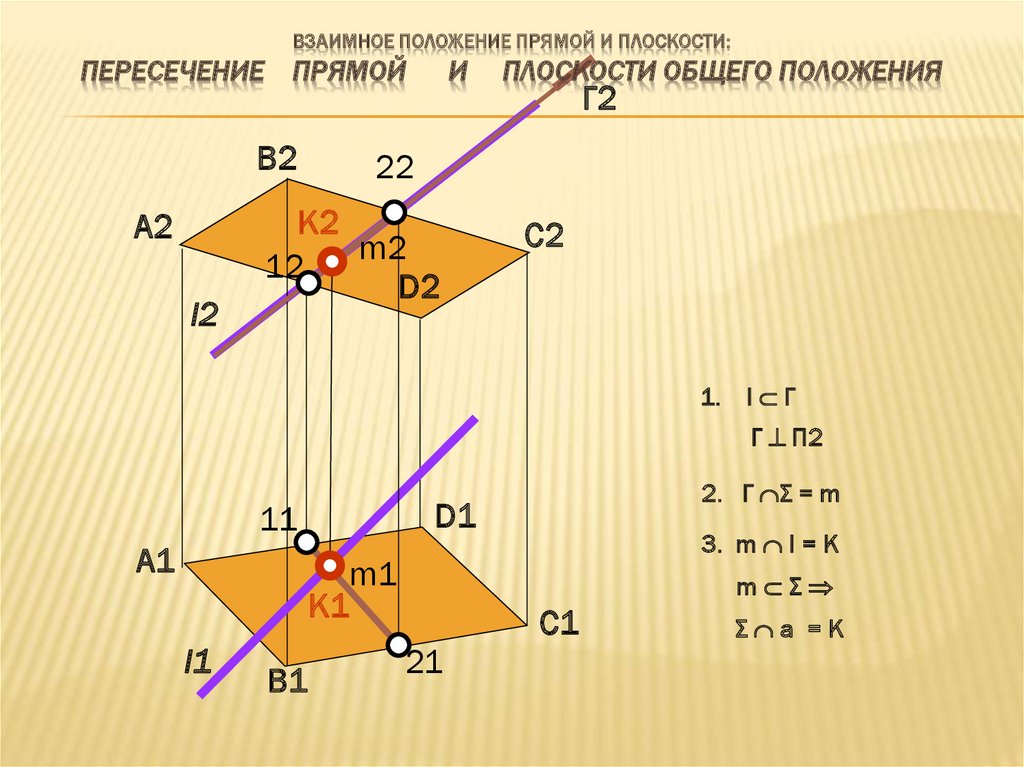
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ:
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ
B2
А2
l2
И
ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
Г2
22
K2
m2
12
D2
C2
1.
l Г
Г П2
D1
11
А1
m1
K1
l1
2. Г Σ = m
B1
3. m l = K
m Σ
C1
21
Σ a =K

19.

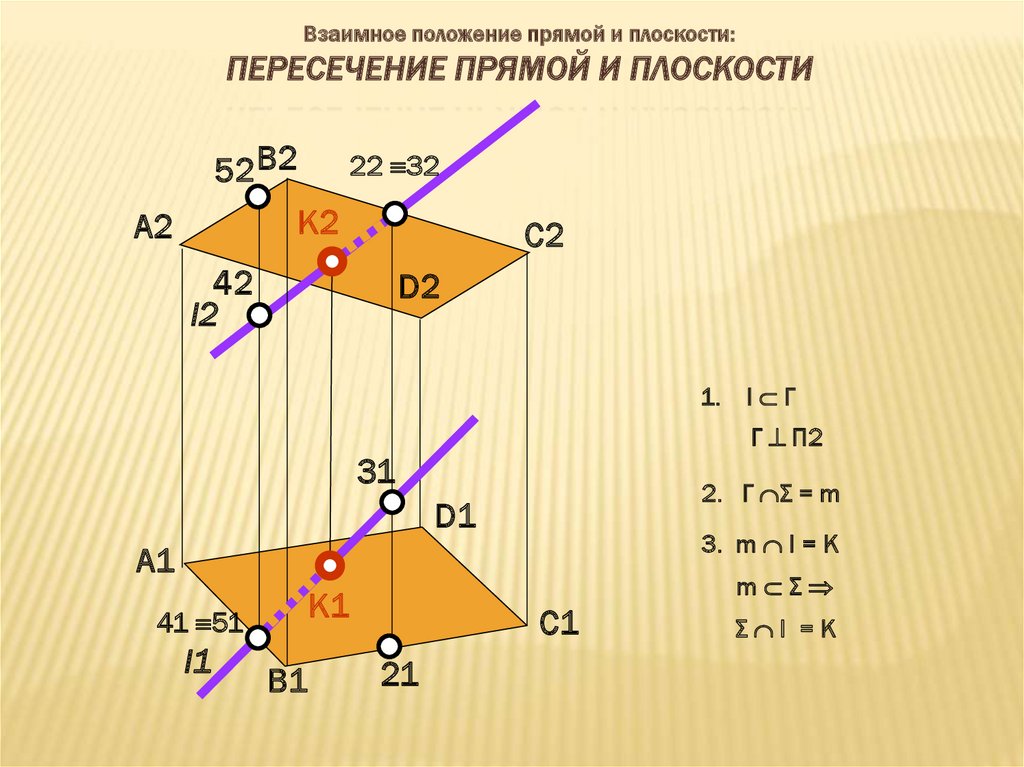
Взаимное положение прямой и плоскости:
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
52 B2
22 32
K2
А2
C2
42
l2
D2
1.
l Г
Г П2
31
2. Г Σ = m
D1
3. m l = K
А1
41 51
l1
m Σ
K1
B1
C1
21
Σ l =K

20. Взаимное положение плоскостей: ПАРАЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ

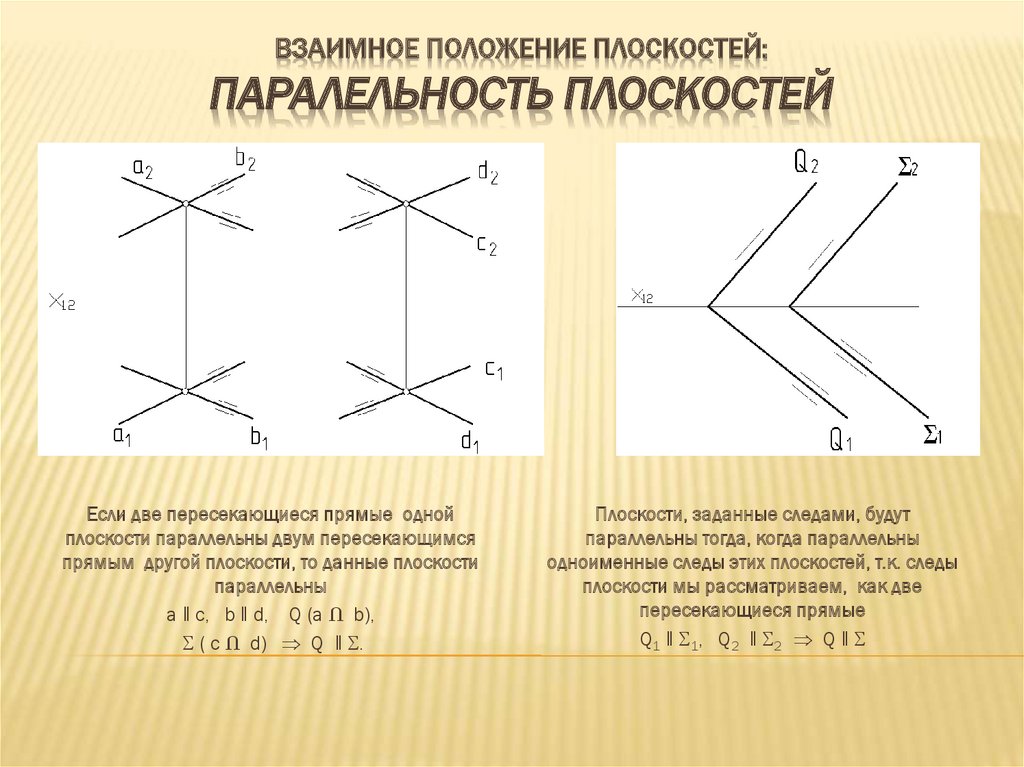
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ:
ПАРАЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Если две пересекающиеся прямые одной
плоскости параллельны двум пересекающимся
прямым другой плоскости, то данные плоскости
параллельны
а ‖ с, b ‖ d, Q (а Ⴖ b),
( с Ⴖ d) Q ‖ .
Плоскости, заданные следами, будут
параллельны тогда, когда параллельны
одноименные следы этих плоскостей, т.к. следы
плоскости мы рассматриваем, как две
пересекающиеся прямые
Q1 ‖ 1, Q2 ‖ 2 Q ‖

21. Взаимное положение плоскостей: ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ

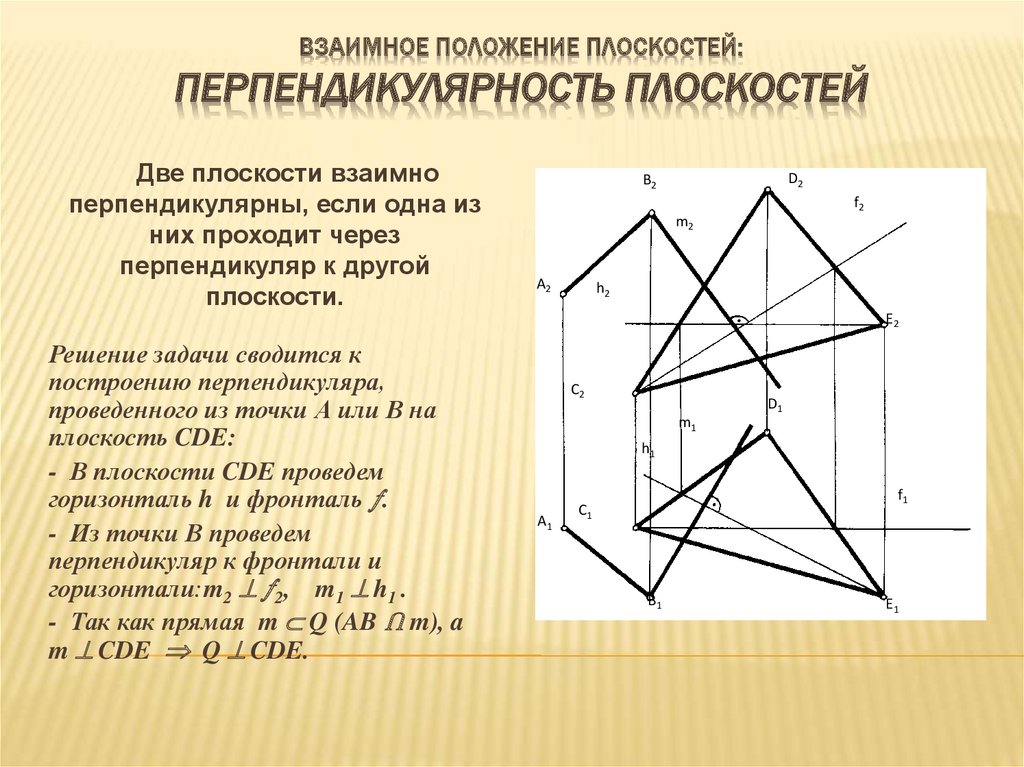
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ:
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Две плоскости взаимно
перпендикулярны, если одна из
них проходит через
перпендикуляр к другой
плоскости.
D2
B2
f2
m2
A2
h2
E2
Решение задачи сводится к
построению перпендикуляра,
проведенного из точки А или В на
плоскость CDE:
- В плоскости CDE проведем
горизонталь h и фронталь .
- Из точки В проведем
перпендикуляр к фронтали и
горизонтали:m2 2, m1 h1 .
- Так как прямая m Q (AB Ⴖ m), a
m CDE Q CDE.
C2
D1
m1
h1
A1
f1
C1
B1
E1

22. Взаимное положение плоскостей: ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ

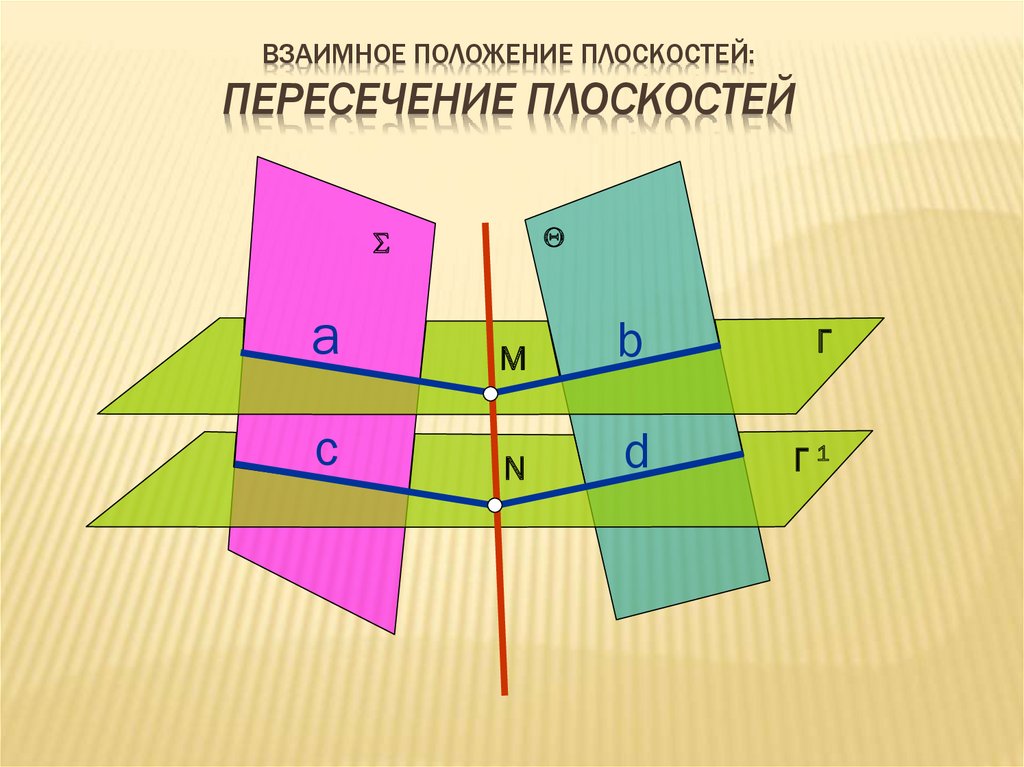
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ:
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Г1
Г
N
M

23.

Взаимное положение плоскостей:
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Г2
B2
E2
D
2
A2
Дано:
Σ( АВС) ll П1 , П2
22
42
( DTF) ll П1 , П2
M2
N2
32
Σ= MN -?
1.
12
C2
F2
D
1
[FE] Г
2. Г Σ = [12]
3. [12] [FE] = M
[12] Σ Σ [FE] = M
31
A1
41
11
N1
4.
E1
C1
M1
B1
5. Г1 Σ = [34]
6. [34] [DF] = N
21
F1
[DF] Г1
[34] Σ Σ [DF] = N
Σ= MN

24.

Взаимное положение плоскостей:
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
Г2
B2
E2
D
2
A2
Σ( АВС) ll П1 , П2
22
62
72
42=5
2 N2
Дано:
( DTF) ll П1 , П2
M2
Σ= MN -?
82
32
1.
12
C2
F2
D
1
[FE] Г
2. Г Σ = [12]
3. [12] [FE] = M
[12] Σ Σ [FE] = M
31
A1
41
11
N1
M1
71
81
61
B1
C1
[DF] Г1
5. Г1 Σ = [34]
6. [34] [DF] = N
21
F1
4.
E1
[34] Σ Σ [DF] = N
Σ= MN

25.

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ:
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
а
М
b
Г
c
N
d
Г1

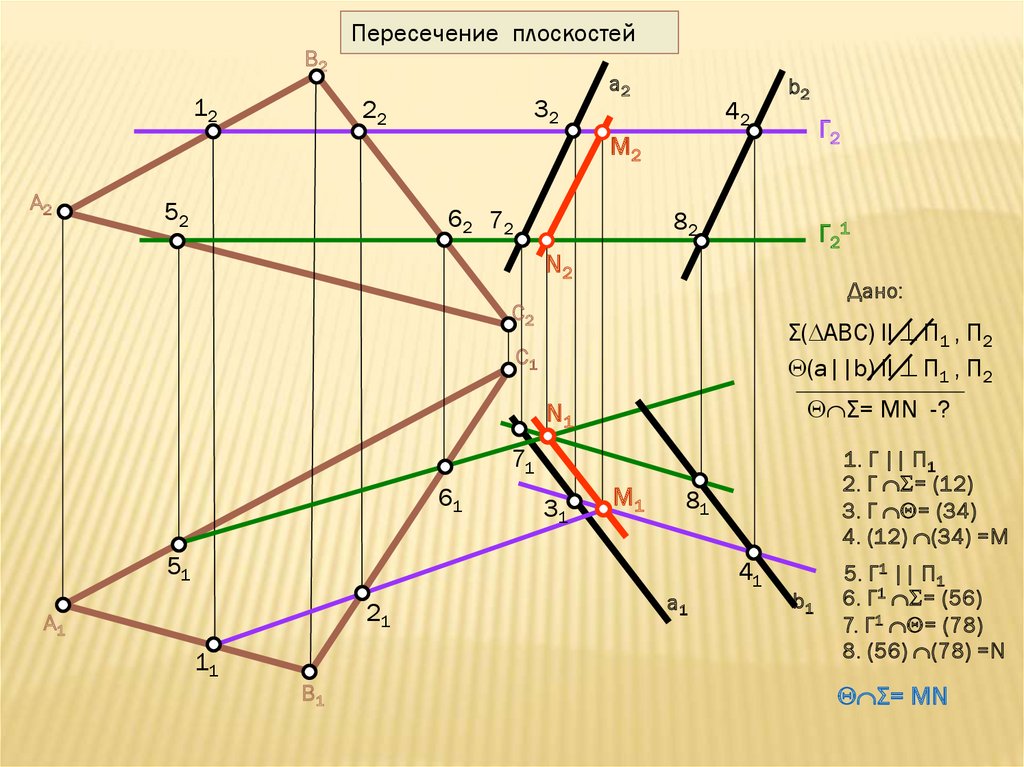
26.

B2
12
Пересечение плоскостей
32
22
а2
42
b2
Г2
M2
A2
52
62 72
82
Г21
N2
Дано:
C2
Σ( АВС) ll П1 , П2
(а||b) ll П1 , П2
C1
Σ= MN -?
N1
71
61
31
M1
81
51
21
A1
11
B1
1. Г || П1
2. Г = (12)
3. Г = (34)
4. (12) (34) =M
а1
41
b1
5. Г1 || П1
6. Г1 = (56)
7. Г1 = (78)
8. (56) (78) =N
Σ= MN