Способы плоскостей и сфер

1.

(Лекция 8)
Пересечение геометрических
объектов общего положения
Красовская Н.И.

2.

(Лекция 8)
решения задач на пересечение
геометрических объектов с
помощью посредников
Красовская Н.И.

3.

Любую точку в пространстве
можно определить:
тремя координатами
(x,y,z)
Красовская Н.И.

4.

пересечением двух линий
(K=a ∩ b)
K
b
a
Красовская Н.И.

5.

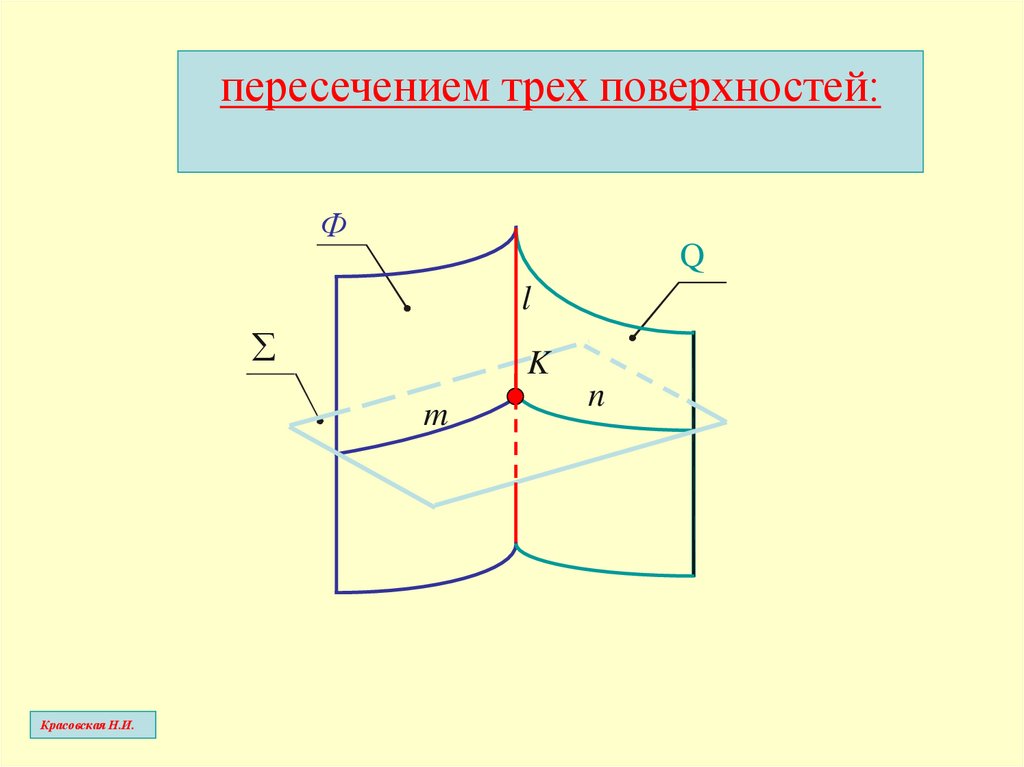
пересечением трех поверхностей:
Ф
Q
l
K
m
Красовская Н.И.
n

6.

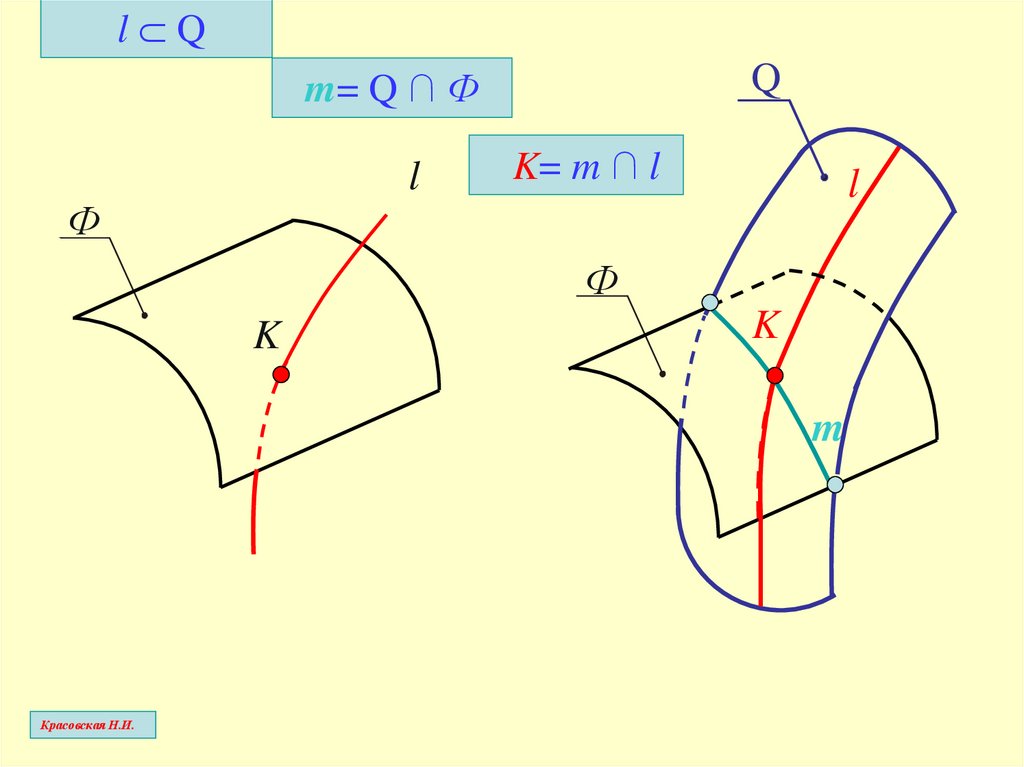
l Q
Q
m= Q ∩ Ф
l
Ф
K= m ∩ l
l
Ф
K
K
m
Красовская Н.И.

7.

Способ
секущих плоскостей
Красовская Н.И.

8.

Алгоритм решения задач
на пересечение прямой линии с плоскостью
1. Прямая заключается в проецирующую плоскость-посредник
2. Строится линия пересечения
плоскости-посредника с заданной плоскостью
3. В пересечении построенной линии пересечения и заданной
прямой
находится искомая точка
4. Определяется видимость
заданной прямой
Красовская Н.И.

9.

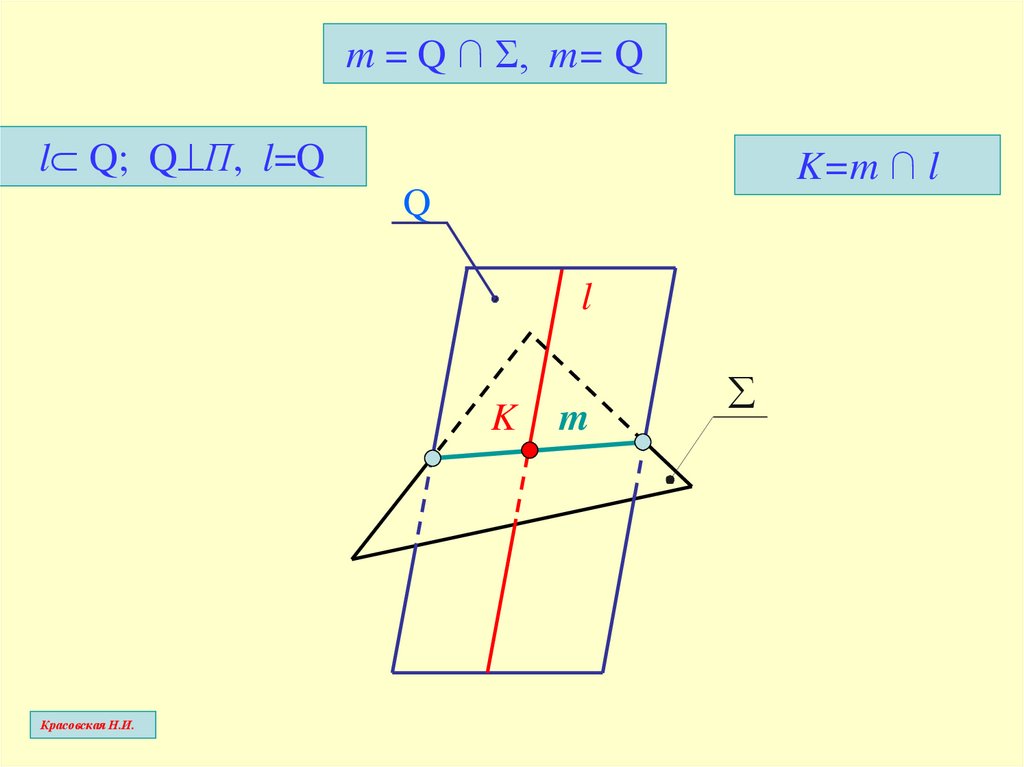
m = Q ∩ Σ, m= Q
l Q; Q П, l=Q
K=m ∩ l
Q
l
K
Красовская Н.И.
m

10.

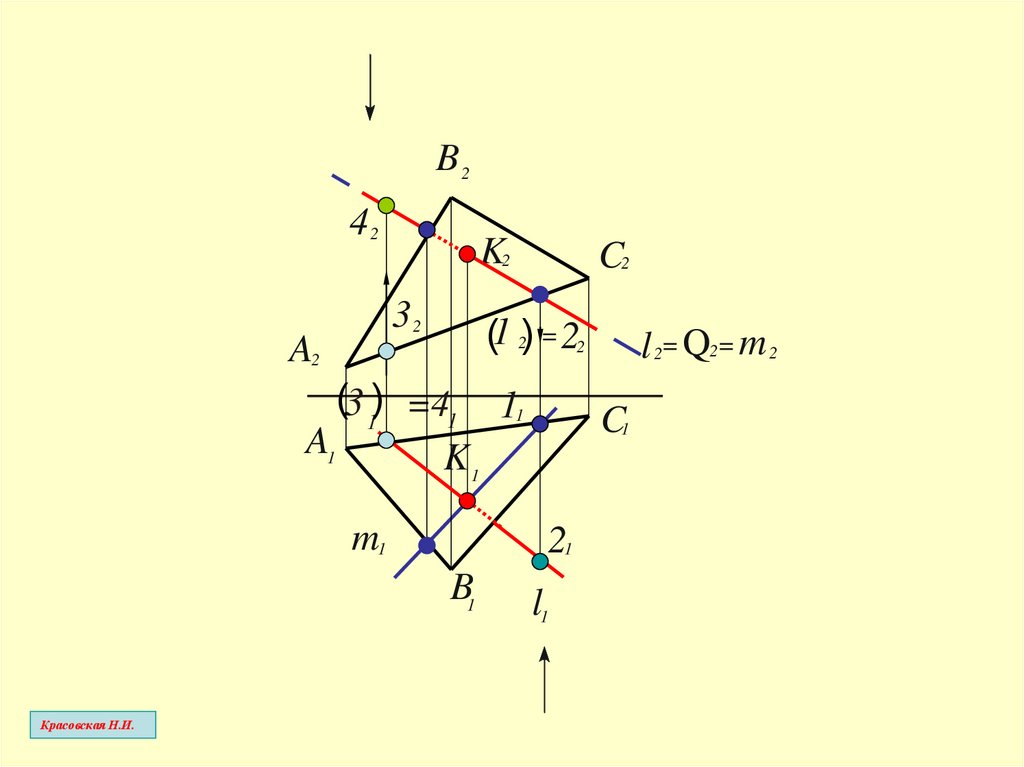
B2
42
K2
32
A2
C2
(1 2) = 22
(3 1) =41 11
A1
K1
m1
Красовская Н.И.
C1
21
B1
l 2= Q2= m 2
l1

11.

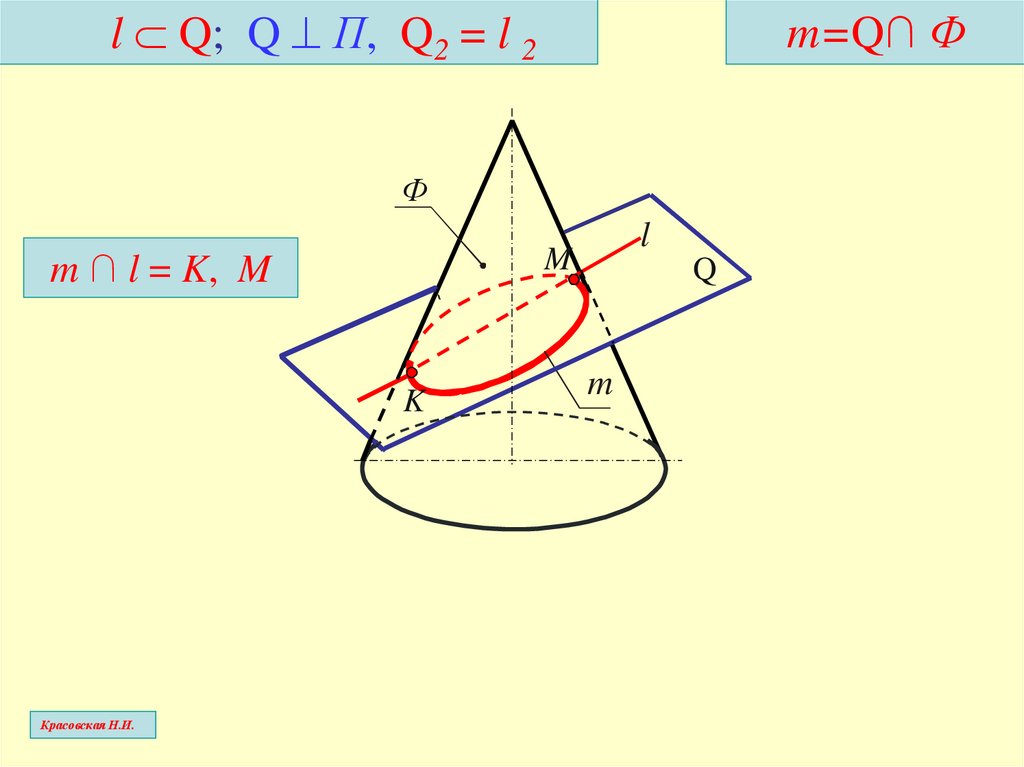
l Q; Q П, Q2 = l 2
m=Q∩ Ф
Ф
m ∩ l = K, M
M
K
Красовская Н.И.
l
Q
m
m

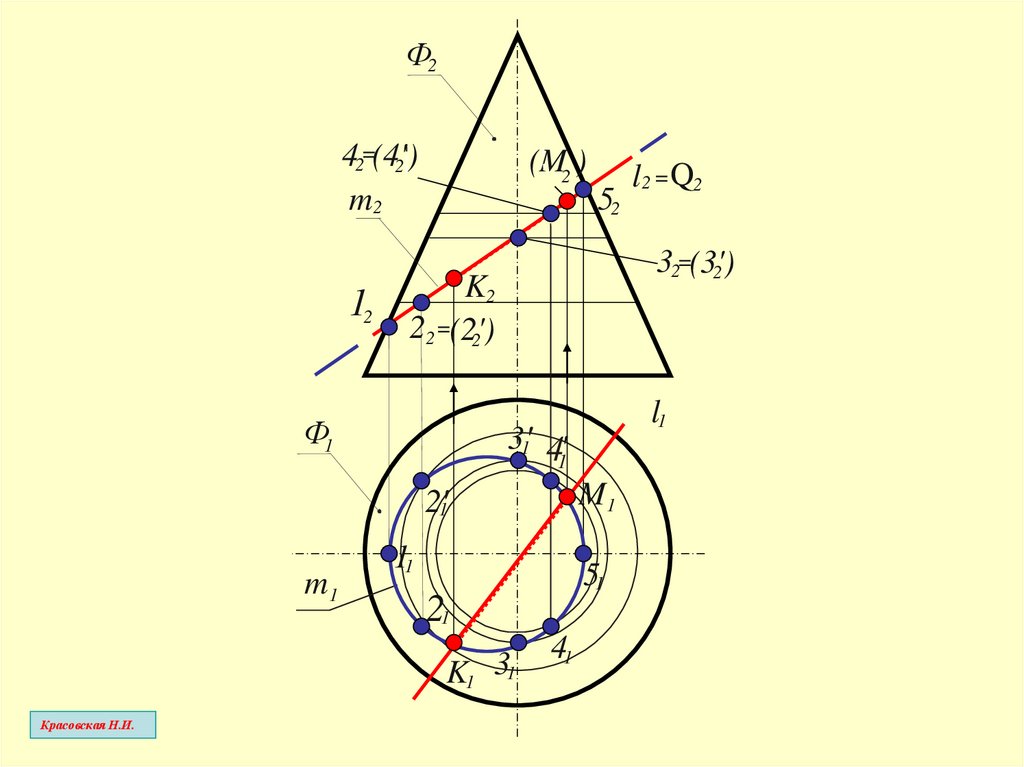
12.

Ф2
42=(4')
2
m2
12
(M2 )
52
32=(3')
2
K2
22 =(2')
2
Ф1
1
M1
11
51
21
K1 31
Красовская Н.И.
l1
3'1' 4'
2'1'
m1
l2 = Q2
41

13.

Алгоритм решения
задачи на пересечение двух плоскостей
1. Заданные плоскости рассекаются
проецирующей плоскостью-посредником
2. Строятся две линии пересечения
вспомогательной плоскости с заданными плоскостями
3. Находится общая точка
для трех плоскостей (на пересечении построенных линий пересечения)
4. Вводится еще одна плоскость – посредник
и пункты 2 и 3 повторяются
5. Через полученные точкипроводится прямая линия,
которая и является графическим результатом решения данной задачи
Красовская Н.И.

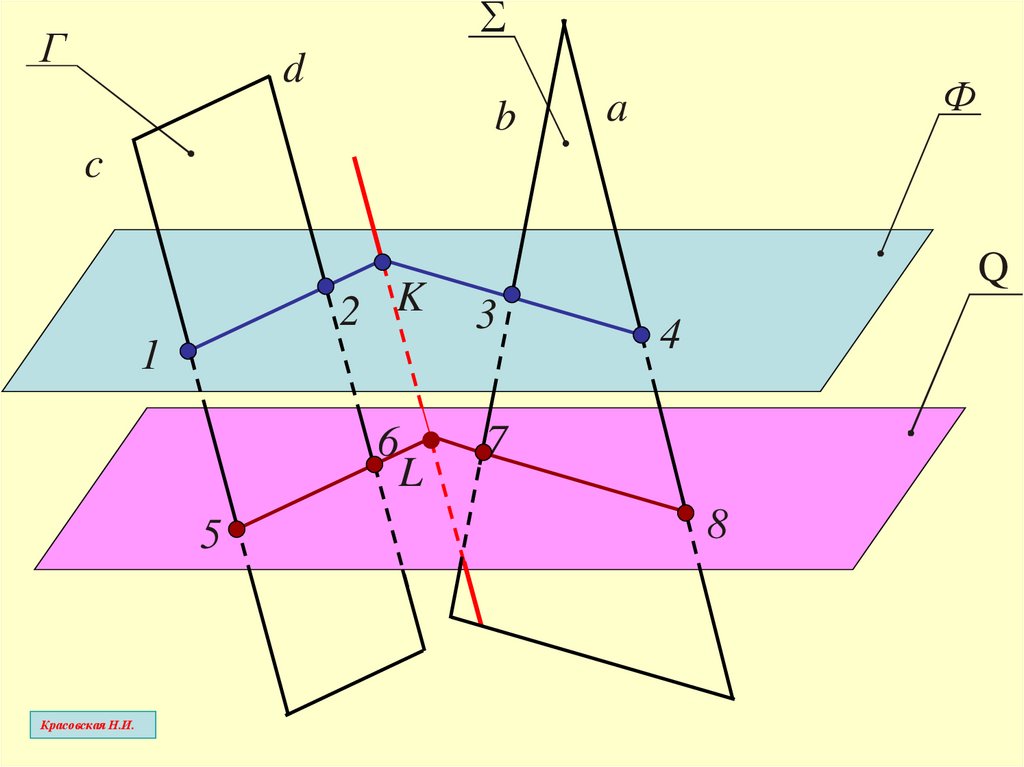
14.

S
Г
d
b
Ф
a
c
Q
2 K
3
6
L
7
1
5
Красовская Н.И.
4
8

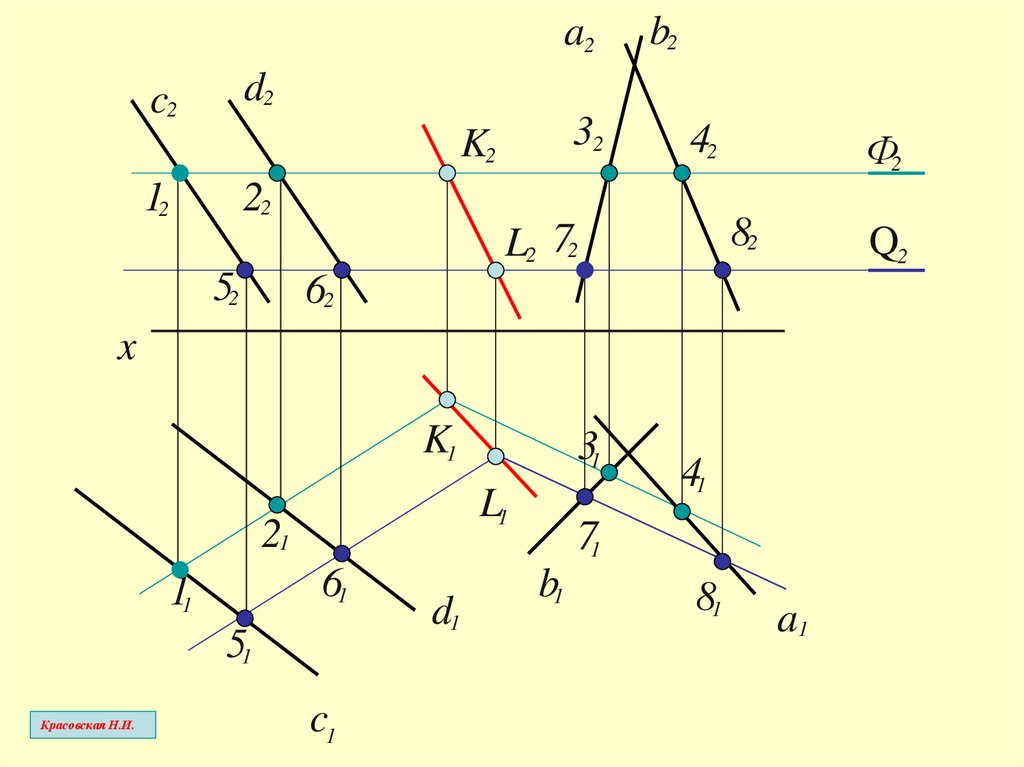
15.

a2
b2
d2
c2
32
K2
12
42
22
82
L2 72
52
Ф2
Q2
62
x
K1
L1
21
61
11
51
Красовская Н.И.
31
c1
d1
41
71
b1
81
a1

16.

Алгоритмы решения задач на
пересечение поверхностей
вращения
Красовская Н.И.

17.

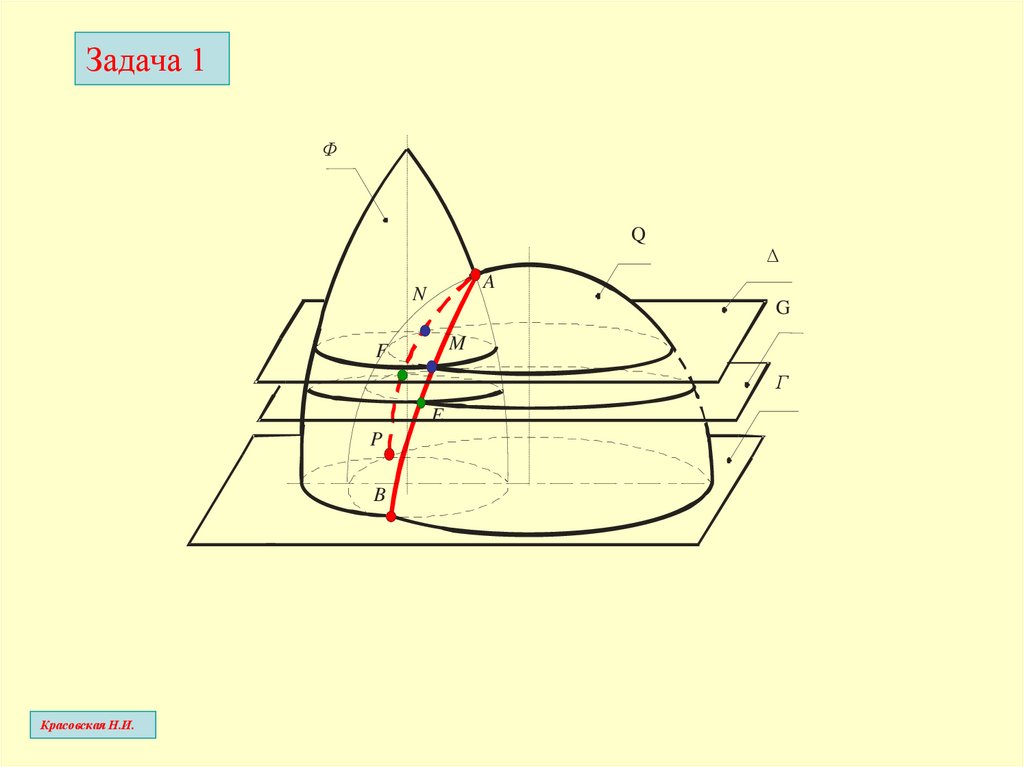
Задача 1
Ф
Q
∆
A
N
G
M
F
Г
E
P
B
Красовская Н.И.

18.

1-й этап:
Определяют опорные точки:
Опорные точки B и P находятся с помощью
плоскости Г.
Наивысшая точка А находится с помощью
общей плоскости симметрии Σ (Σ1).
Красовская Н.И.

19.

2-й этап:
– между опорными точками
вводится плоскость-посредник ∆(∆ 2)||П1;
– cтроятся линии пересечения
плоскости с поверхностями Ф и Q;
–
Красовская Н.И.
определяются точки пересечения
построенных линий пересечения

20.

1-й этап
Ф
2
A2
2-й этап
Q2
Ф
В2=(Р2)
2
Г
2
A2
P1
Q2
∆2
M 2 = (N 2 )
A
1
Σ
В2=(Р2)
1
P
Q
1
Ф
Г
2
1
N
1
1
B
1
A
M
Ф
1
Красовская Н.И.
B1
1
Σ
1
1
Q1

21.

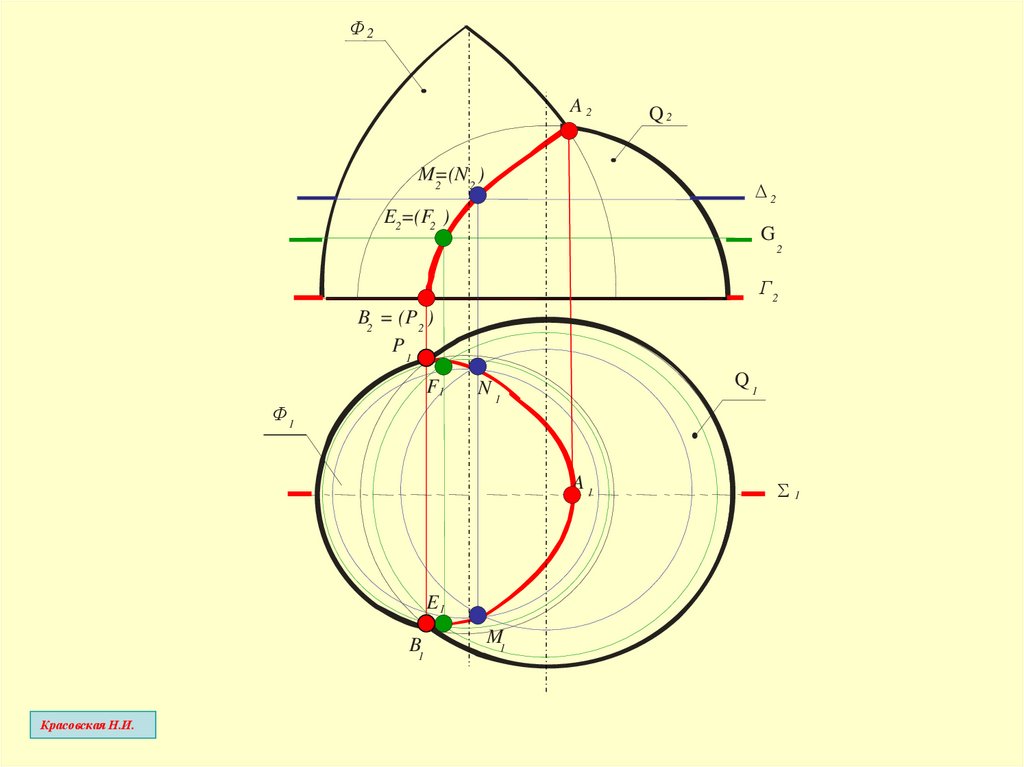
3-й этап:
– вводится еще ряд посредников между опорными
точками, и все построения повторяются;
– построенные точки соединяются плавной кривой с
учетом их видимости
Красовская Н.И.

22.

Ф2
A2
M=(N
)
2
2
Q2
∆2
E2=(F2 )
G
2
Г2
B2 = (P2 )
P
1
F1
Ф1
Q1
N1
A1
E1
B1
Красовская Н.И.
M1
Σ1

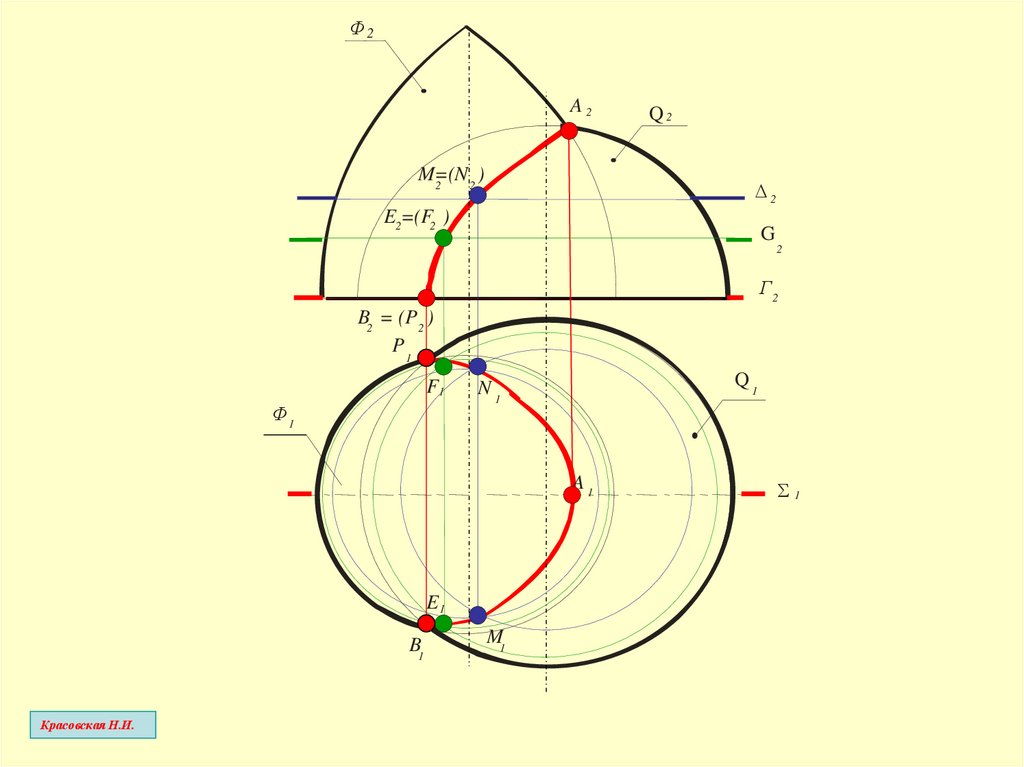
23.

Ф2
A2
M=(N
)
2
2
Q2
∆2
E2=(F2 )
G
2
Г2
B2 = (P2 )
P
1
F1
Ф1
Q1
N1
A1
E1
B1
Красовская Н.И.
M1
Σ1

24.

Ф2
Q2
A2
F2= (E2 )
D2= (C2 )
2
Т2
Г2
N2 =(M 2 )
В2
С1
E1
(M1 )
A1
F1
D1
Красовская Н.И.
Ф1
1
(B1 )
(N1 )
Q1

25.

Выводы
– для удобства плоскости-посредники должны
быть проецирующими
– а для решения второй позиционной задачи
плоскости-посредники должны занимать
положение уровня
Красовская Н.И.

26.

(Лекция 9)
Алгоритм решения второй
позиционной задачи с
помощью секущих сфер
Красовская Н.И.

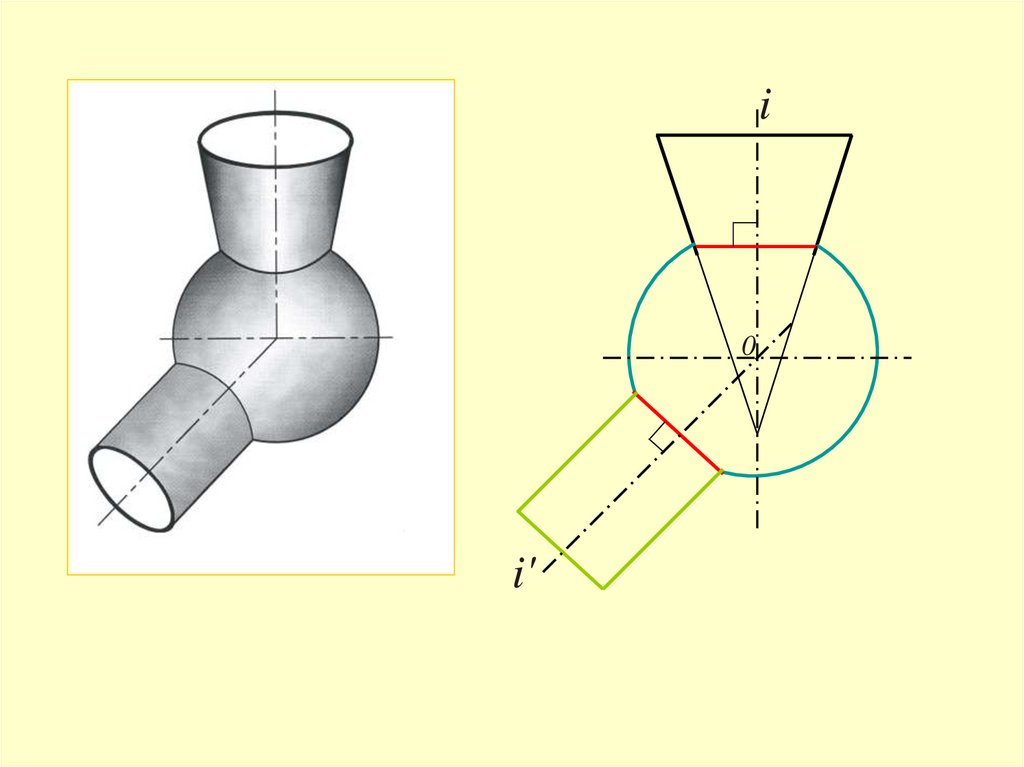
27.

Две любые соосные поверхности вращения
пересекаются по окружностям
(параллелям), проходящим через точки
пересечения меридианов поверхностей

28.

ii
0
0
i'
i'

29.

1. Если оси поверхностей пересекаются, то для
определения линии пересечения поверхностей
используют семейство концентрических сфер
2. Если оси не пересекаются, применяют
эксцентрические сферы

30.

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ
СПОСОБОМ
КОНЦЕНТРИЧЕСКИХ СФЕР

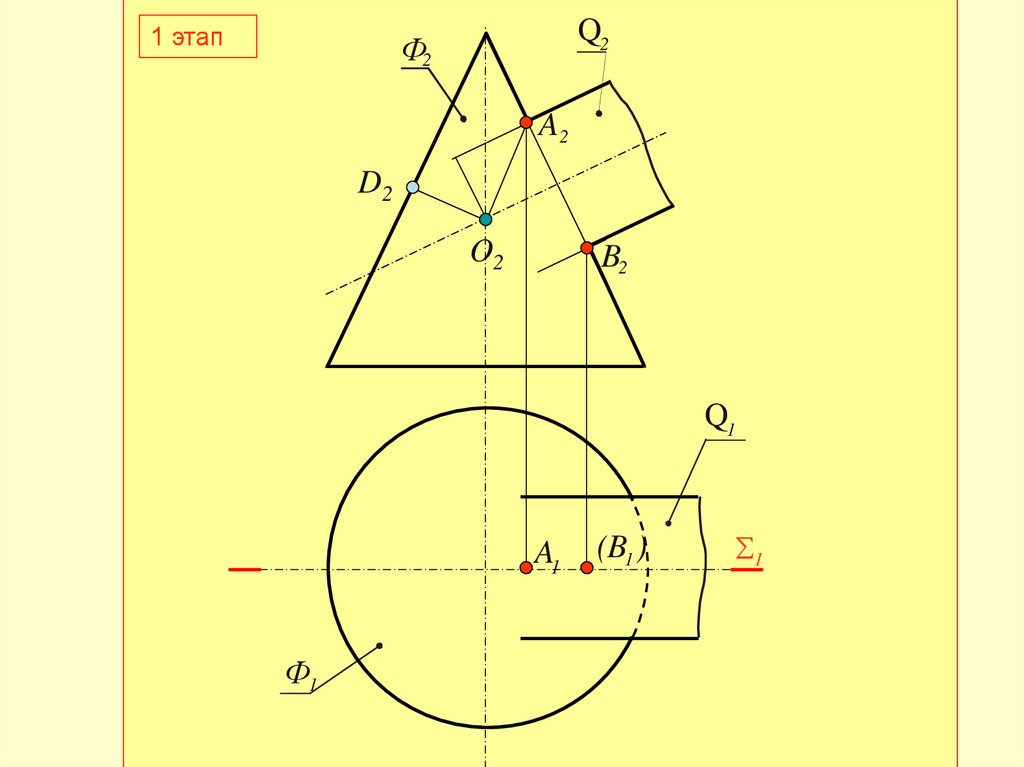
31.

1-й этап :
– обозначается плоскость
симметрии Σ(Σ1)
В пересечении главных меридианов
определяются опорные точки - A и B

32.

Плоскость симметрии должна
быть плоскостью уровня

33.

–определяется центр вспомогательных
секущих сфер - О
Он находится в точке пересечения осей
данных поверхностей

34.

– определяются радиусы максимальной и минимальной
вспомогательных сфер
За Rmax принимается расстояние до наиболее удаленной
от центра сфер опорной точки
Rmax = О2 А2
За Rmin принимается величина большей нормали
Rmin = О2 D2
D2 – точка касания сферы с поверхностью

35.

1 этап
Q2
Ф2
A2
D2
O2
B2
Q1
A1
Ф1
(B1 )
1

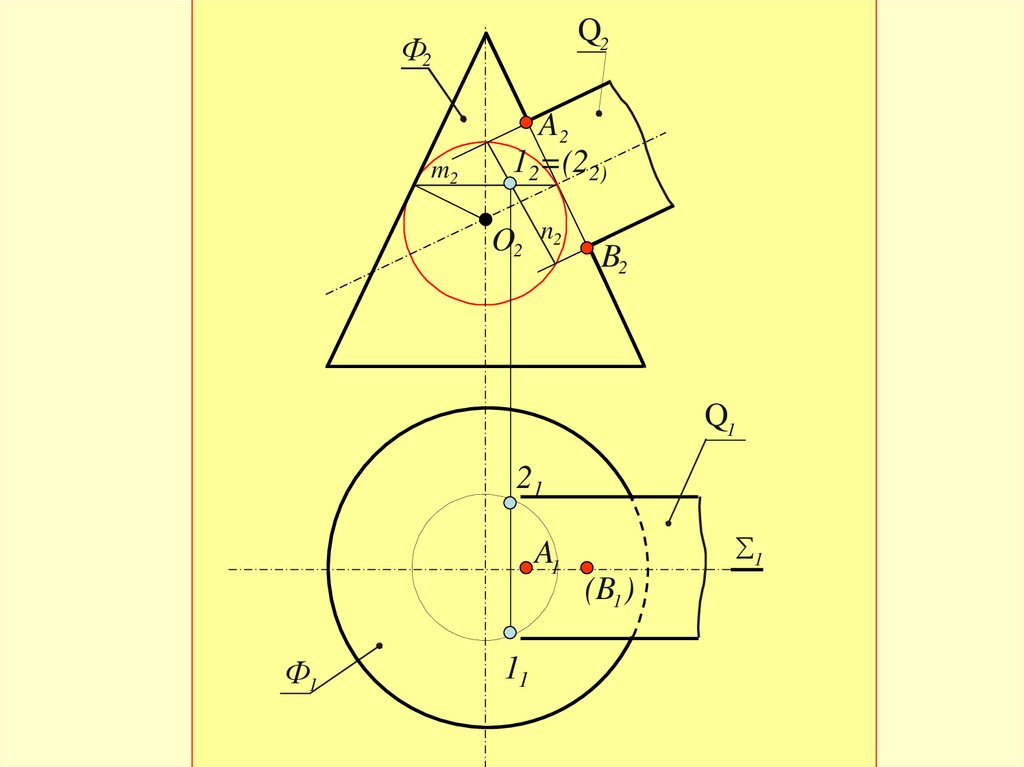
36.

2-й этап:
проводится сфера минимального радиуса
строятся окружности пресечения ее с
заданными поверхностями –
mиn
-определяются точки пересечения этих
окружностей –
m∩ n =1,2

37.

Q2
Ф2
m2
A2
12=(22)
O2 n2
B2
Q1
21
A1
Ф1
11
1
(B1 )

38.

3-й этап:
– для определения достаточного
количества точек линии пересечения
из центра О
проводится семейство секущих сфер
с радиусом в пределах
Rmin R Rmax

39.

Соединив
одноименные проекции точек плавной
кривой линией,
получают проекции искомой линии
пересечения данных поверхностей

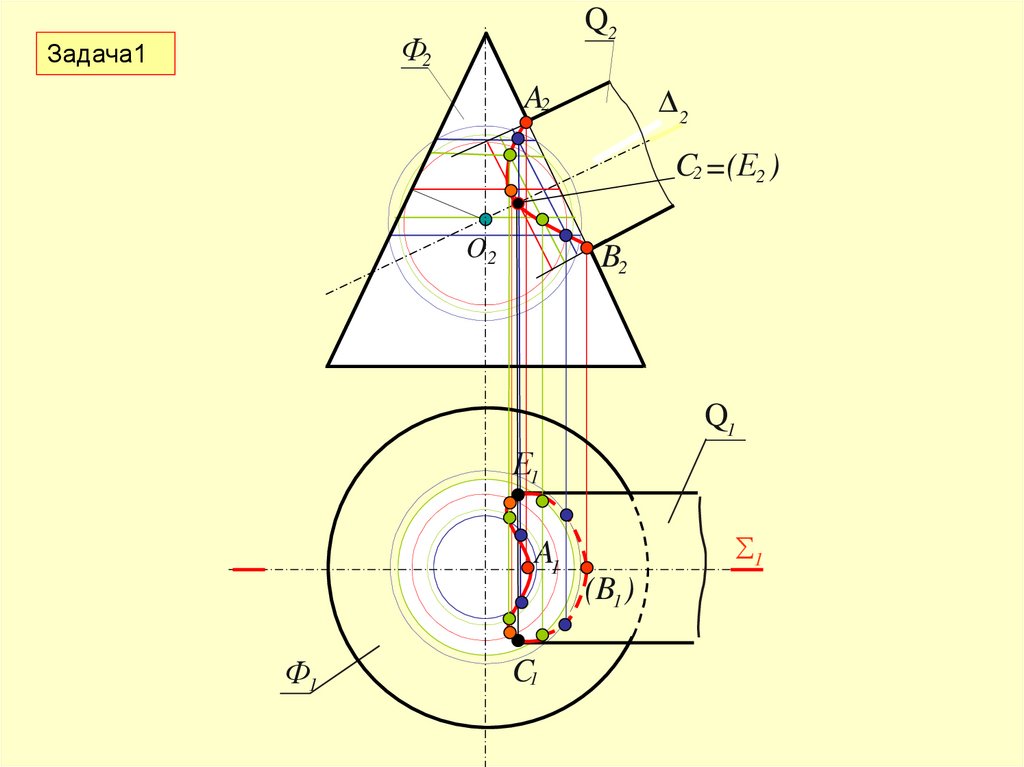
40.

Q2
Ф2
Задача1
D2
A2
C2 =(Е2 )
O2
B2
Q1
Е1
A1
Ф1
C1
1
(B1 )

41.

Границей видимости
линии пересечения на горизонтальной
плоскости проекций является плоскость
D(D2)
Часть линии пересечения, расположенная
выше плоскости, видима, а ниже плоскости
D(D2) – нет

42.

Частные случаи
взаимного пересечения
поверхностей второго
порядка

43.

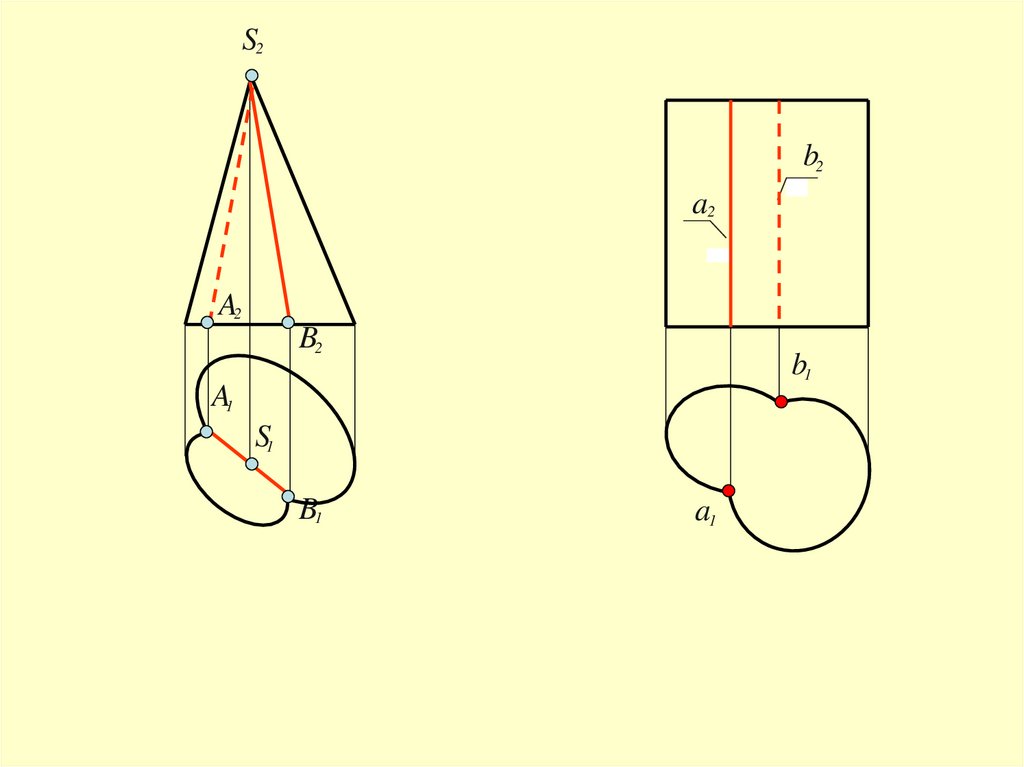
При пересечении двух линейчатых поверхностей могут
получиться и прямые линии
– общие образующие этих поверхностей
например:
-при пересечении двух конических поверхностей с
общей вершиной
-при пересечении двух цилиндрических поверхностей с
параллельными образующими

44.

S2
b2
a2
A2
B2
b1
A1
S1
B1
a1

45.

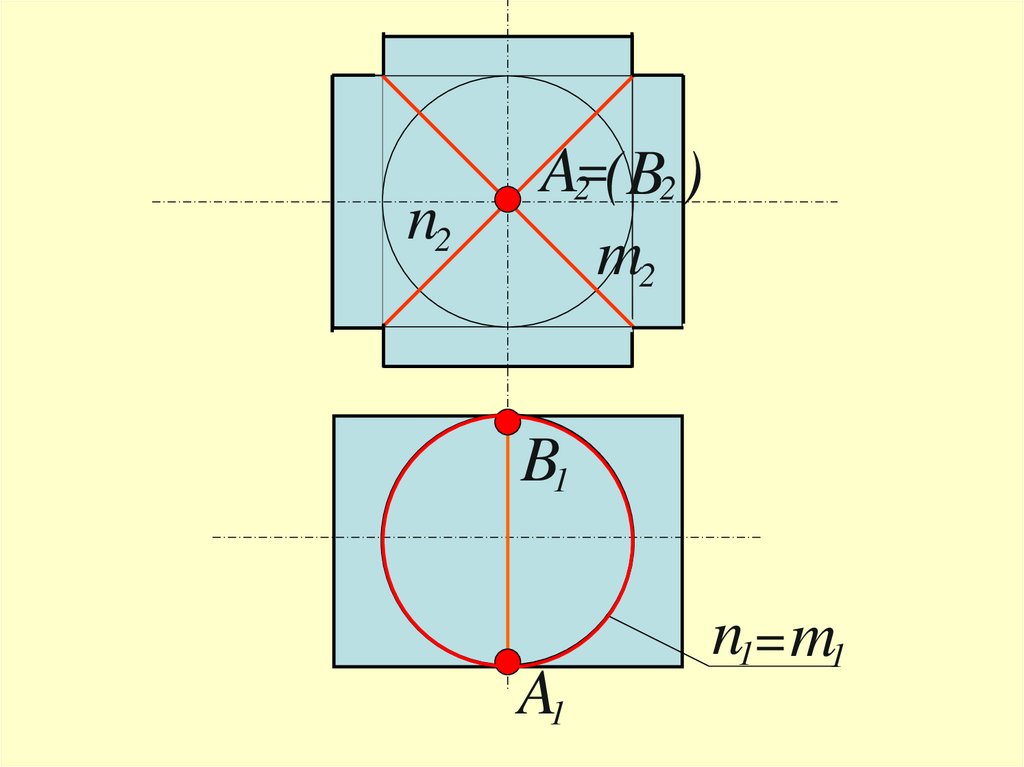
Теорема Монжа

46.

Если две поверхности второго порядка
описаны
около третьей поверхности второго порядка
(или вписаны в неё),
то они пересекаются
по двум плоским кривым второго порядка,
плоскости которых проходят через
прямую, соединяющую
точки пересечения линий касания

47.

n2
A2=(B2 )
m2
B1
A1
n1= m1

48.

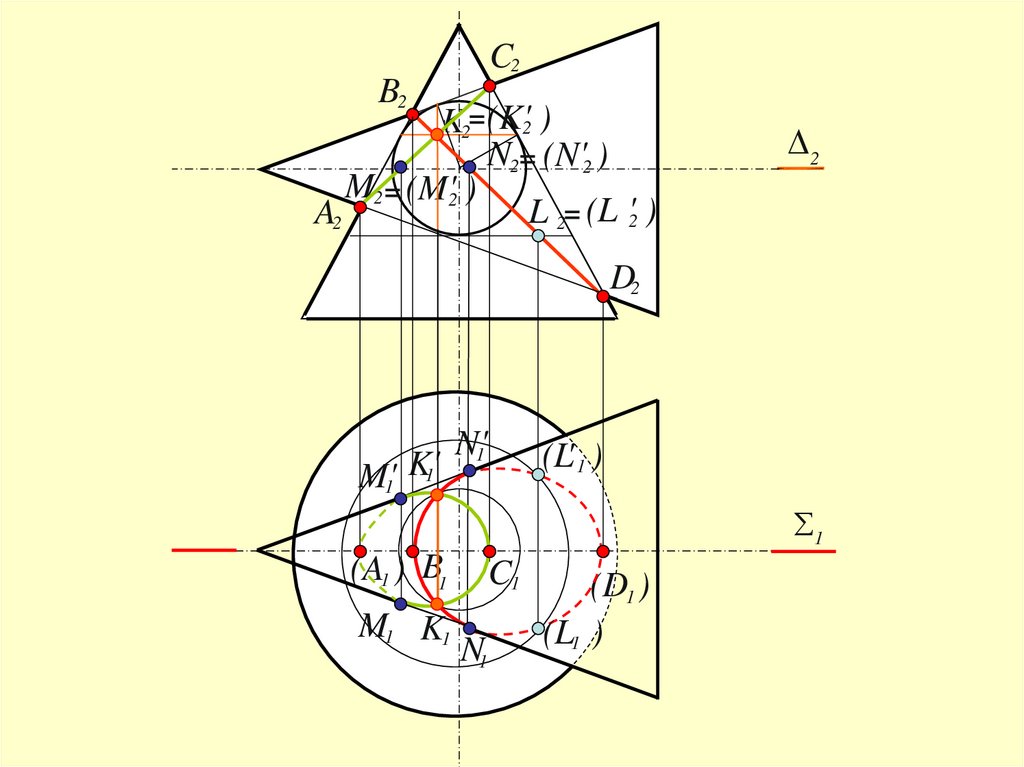
49.

C2
B2
K2= (K'2 )
N2= (N'2 )
M2 = (M'2 )
L 2= (L '2 )
A2
D2
D2
M'1 K'1
N'1
(L' 1 )
1
(A1 ) B1
M1 K1
C1
N1
(D1 )
(L1 )

50.

Выводы
- концентрические сферы-посредники для построения
линии пересечения двух поверхностей вращения вводятся
из точки пересечения осей поверхностей
- радиусы сфер берутся в пределах Rmin R Rmax
- перед тем, как вводить сферы, всегда определяют
опорные точки
- перед тем, как изобразить линию пересечения, всегда
определяют точки, лежащие на границе видимости