Лекция 3. Ранг матрицы. Теория СЛАУ. Проверка СЛАУ на совместность-1

1. Линейная алгебра.

ЛЕКЦИЯ 3
Линейная алгебра.
Ранг матрицы.
СЛАУ в линейной алгебре

2. План лекции

Ранг матрицы
Теория СЛАУ
Проверка СЛАУ на совместность

3. ВОПРОСЫ ДЛЯ ПОВТОРЕНИЯ

1.
2.
3.
4.
5.
6.
7.
8.
9.
Что такое детерминант матрицы?
У какой матрицы невозможно найти детерминант?
От чего зависит способ нахождения детерминанта?
Может ли детерминант быть равным 0? О чем это
говорит?
Что такое Минор элемента матрицы?
Чем отличаются минор и алгебраическое
дополнение?
Что такое союзная (присоединенная) матрица?
Какую роль присоединенная матрица играет в
нахождении обратной матрицы?
У какой матрицы не может быть обратной?

4.

РАНГ МАТРИЦЫ –
- это ещё одна важная
характеристика матрицы, а также
мощный инструмент, который
может помочь решить многие
математические и научные задачи
r(A), rg(A), rang(A), rank(A)
В отличие от детерминанта ранг можно
определить для любой матрицы

5.

6.

7.

8.

9.

10.

11.

12.

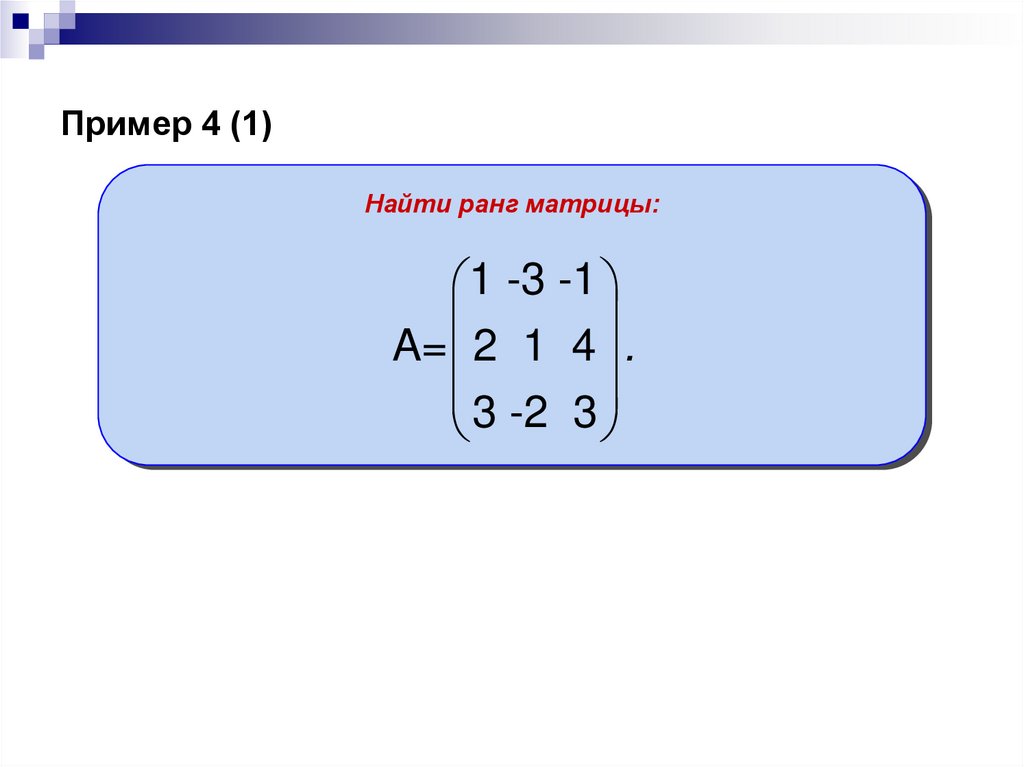
13. Пример 4 (1)

Найти ранг матрицы:
1 -3 -1
A= 2 1 4 .
3 -2 3

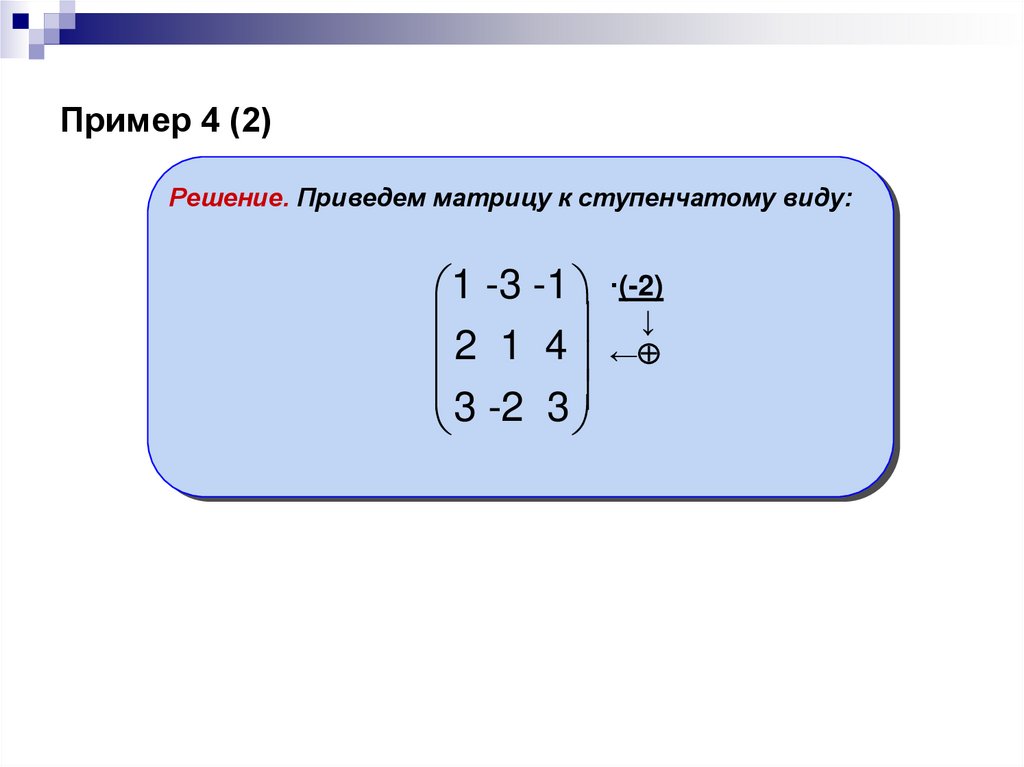
14. Пример 4 (2)

Решение. Приведем матрицу к ступенчатому виду:
1 -3 -1 ·(-2)
↓
2 1 4 ←
3 -2 3

15. Пример 4 (3)

Решение.
1 -3 -1
1 -3 -1 ·(-2)
↓
2 1 4 ← 0 7 6
3 -2 3
3 -2 3

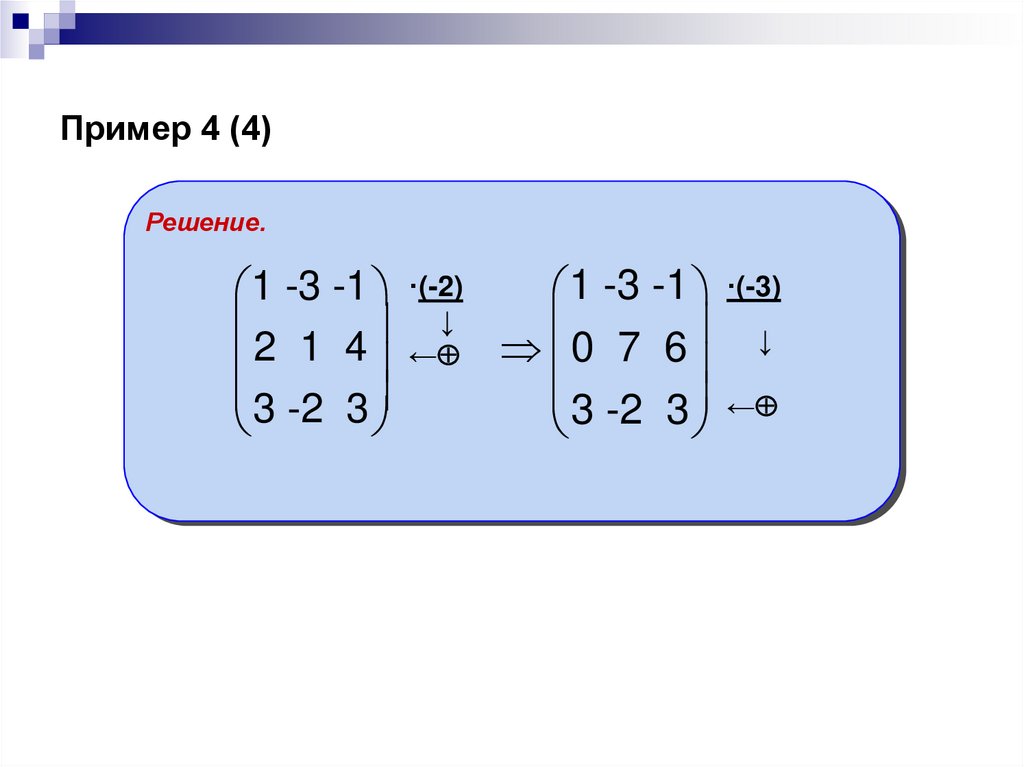
16. Пример 4 (4)

Решение.
1 -3 -1 ·(-3)
1 -3 -1 ·(-2)
↓
↓
2
1
4
0
7
6
←
3 -2 3
3 -2 3 ←

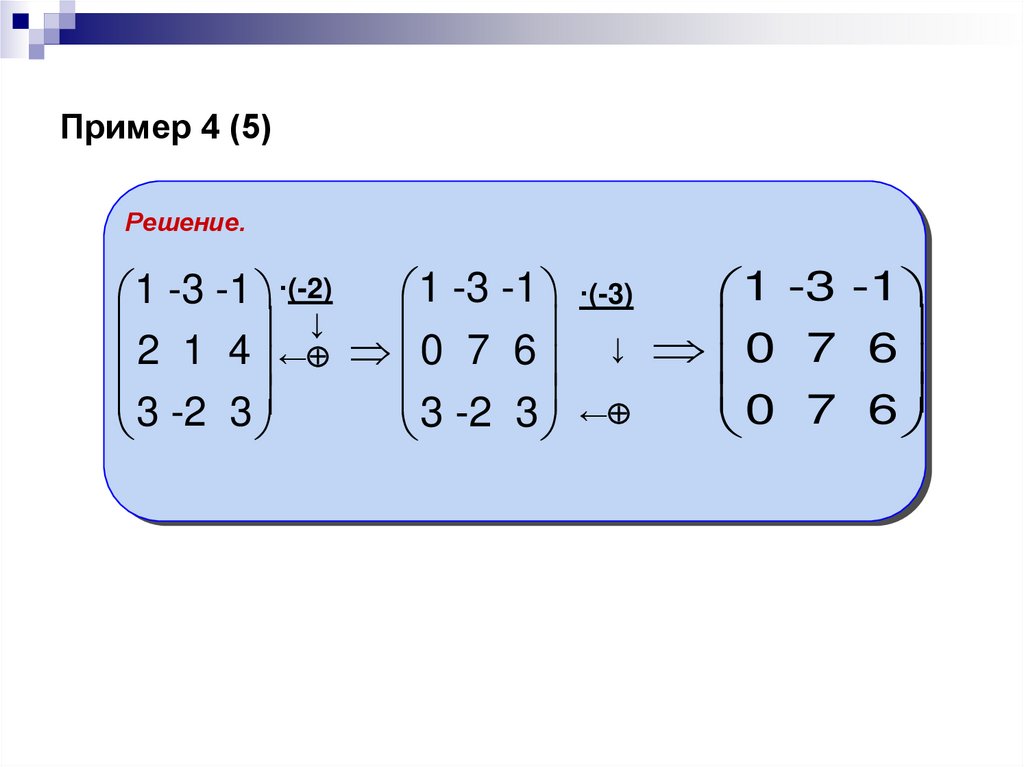
17. Пример 4 (5)

Решение.
1 -3 -1
1 -3 -1 ·(-3)
1 -3 -1 ·(-2)
↓ 0 7 6
↓
2 1 4 ← 0 7 6
0 7 6
3 -2 3
3 -2 3 ←

18. Пример 4 (6)

Решение.
1 -3 -1
1 -3 -1
·(-1) 0 7 6
0
7
6
↓
0 0 0
0 7 6
←

19. Пример 4 (7)

Решение.
1 -3 -1
1 -3 -1
1 -3 -1
·(-1) 0 7 6
0 7 6
0 7 6 ↓
0 0 0
0 7 6
←
r(A)=2

20.

20

21.

Математика – наука молодых. Иначе и не может быть. Занятия
математикой – это такая гимнастика ума, для которой нужны
вся
гибкость
и
вся
выносливость
молодости.
Н.
Винер
К решению систем линейных алгебраических уравнений сводятся
многочисленные практические задачи (по некоторым оценкам более 75%
всех задач).
Можно с полным основанием утверждать, что решение линейных систем
является одной из самых распространенных и важных задач
вычислительной математики.
Конечно, существует много методов и современных пакетов прикладных
программ для решения СЛАУ, но для того, чтобы их успешно
использовать, необходимо разбираться в основах построения методов и
алгоритмов, иметь представления о недостатках и преимуществах
используемых методов.
21

22. Определение СЛАУ

a11x1 a12 x2 a13 x3 ... a1n xn b1
a x a x a x ... a x b
21 2 22 2 23 3
2n n
2
.......................................................
am1 x1 am 2 x2 am3 x3 ... amn xn bm
5х+2y+2z=15
3x-y=11
-2x-4y+z=7
5 2 2
3 -1 0
-2 -4 1
Система линейных алгебраических уравнений — это набор из i
уравнений, j переменных и вектора свободных членов. Прилагательное
«линейных» означает, что все переменные имеют первую степень.
22

23. Определение СЛАУ

23

24. ПРИМЕР

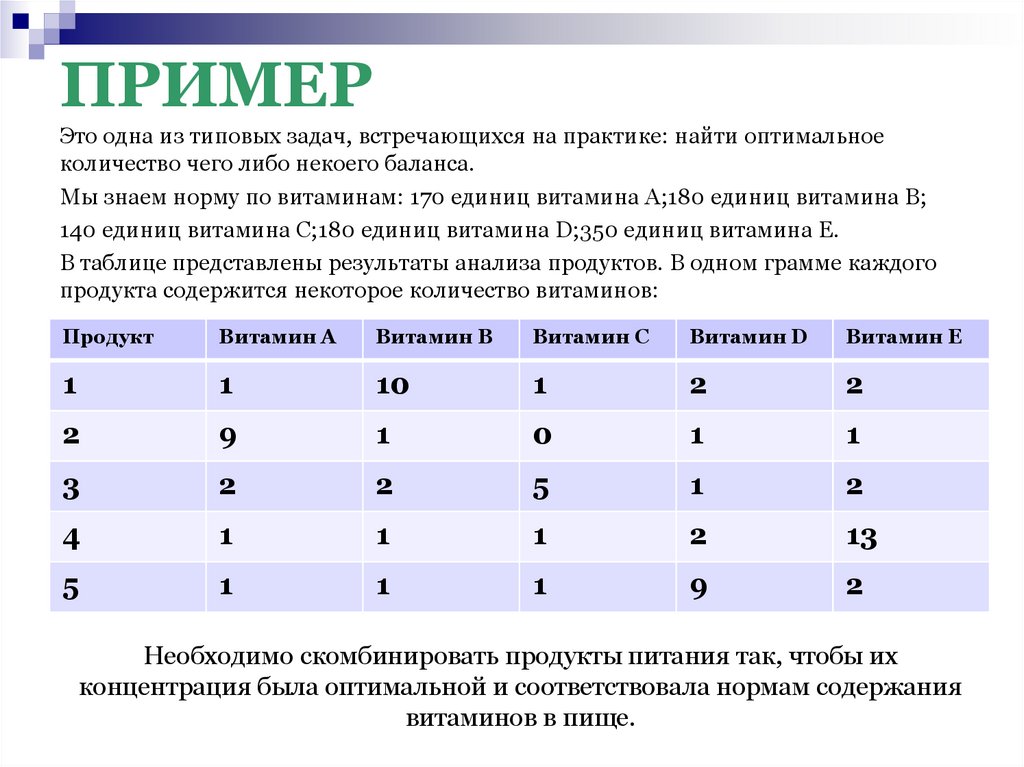
Это одна из типовых задач, встречающихся на практике: найти оптимальное
количество чего либо некоего баланса.
Мы знаем норму по витаминам: 170 единиц витамина А;180 единиц витамина B;
140 единиц витамина С;180 единиц витамина D;350 единиц витамина Е.
В таблице представлены результаты анализа продуктов. В одном грамме каждого
продукта содержится некоторое количество витаминов:
Продукт
Витамин A
Витамин B
Витамин C
Витамин D
Витамин E
1
1
10
1
2
2
2
9
1
0
1
1
3
2
2
5
1
2
4
1
1
1
2
13
5
1
1
1
9
2
Необходимо скомбинировать продукты питания так, чтобы их
концентрация была оптимальной и соответствовала нормам содержания
витаминов в пище.

25. ПРИМЕР

Продукт
Витамин A
Витамин B
Витамин C
Витамин D
Витамин E
1
1
10
1
2
2
2
9
1
0
1
1
3
2
2
5
1
2
4
1
1
1
2
13
5
1
1
1
9
2
Обозначим оптимальную концентрацию (количество единиц) для продукта 1
как x1, для продукта 2 — как x2 и так далее.

26.

Относительно системы уравнений нас интересуют ответы на
следующие вопросы:
1. Совместна система или нет?
2. Если система совместна, то имеет ли она единственное решение
или нет?
3. Если решение единственное, то как его найти?
4. Если система имеет бесконечно много решений, то какова
структура множества решений?
5. Как в бесконечном множестве решений системы определить
одно решение, наилучшее с практической точки зрения?
6. Если система несовместна, то как определить ее приближенное
решение?
26

27. Определение СЛАУ

27

28. Определение СЛАУ

28

29. Определение СЛАУ

29

30. Исследование СЛАУ на совместность

Исследование
СЛАУ наисследовать
Таким образом, есть необходимость
СЛАУ на совместность, то есть доказать, что какоесовместность
либо решение вообще существует. Ключевую роль в
такой проверке играет теорема Кронекера-Капелли:
Система линейных уравнений
совместна тогда и только тогда, когда ранг ее
матрицы системы совпадает с рангом
расширенной матрицы системы.

31. Исследование СЛАУ на совместность

1.
2.
Если ранг матрицы системы равен рангу расширенной
матрицы системы, то система совместна, причём, если данное
число (РАНГ) совпадает с количеством неизвестных, то решение
единственно.
Если РАНГ при этом меньше числа неизвестных, то СЛАУ
имеет бесконечное число решений.
3. Если ранг расширенной матрицы больше ранга
матрицы системы, система несовместна.