Лекция_10

1.

§ 6. Свойства функций, непрерывных на отрезке
Функцию y f x называют непрерывной в интервале a, b , если
она непрерывна в каждой точке этого интервала.
Функцию y f x называют непрерывной на отрезке a, b , если
она непрерывна в интервале a, b и в точке x a непрерывна справа
lim f x f a , а в точке x b непрерывна слева lim f x f b .
x a 0
x b 0
Пусть функция y f x определена на некотором множестве D
значений аргумента. Функцию y f x называют ограниченной на
множестве D, если существует положительное число М такое, что для
всех значений x из множества D выполняется неравенство f x M .
Если такого числа М не существует, то функцию y f x называют
неограниченной на множестве D.
Свойства функций непрерывных на отрезке.
Теорема Вейерштрасса. Если функция непрерывна на отрезке, то
она достигает на этом отрезке своего наибольшего и наименьшего
значений.
Следствие. Если функция непрерывна на отрезке, то она ограничена
на отрезке.

2.

Теорема Больцано-Коши. Если функция y f x непрерывна на
отрезке a; b и принимает на его концах неравные значения f a A и
f b B , то на этом отрезке она принимает и все промежуточные
значения между A и B.
Следствие. Если функция y f x непрерывна на отрезке a; b и
принимает на его концах значения разных знаков, то внутри отрезка
a; b найдется хотя бы одна точка c, в которой данная функция
обращается в нуль: f c 0 .

3.

§ 7. Производная и дифференциал функции
Производной функции y f x в точке x называют предел
отношения приращения функции к приращению аргумента, когда
приращение аргумента стремится к нулю:
f x x f x
y
lim
lim
.
x 0
x 0 x
x
Если этот предел конечный, то функцию
f x называют
дифференцируемой в точке x. В этом случае она оказывается еще и
непрерывной в этой точке. Нахождение производной называют
дифференцированием функции.
dy df x
Обозначения производной: y , y x , f x , f x ,
,
.
dx dx
Пример. Найти производную функции y x 2 .
y
x x x 2
y lim
lim
lim 2 x x lim 2 x lim x 2 x .
x 0 x
x 0
x 0
x 0
x 0
x
Некоторые формулы дифференцирования.
1) c 0 , c постоянная;
2

4.

nx
2) x
n
n 1
;
3) cy cy , c постоянная;
4) u v u v ;
5) uv u v uv ;
u u v v u
6)
;
2
v
v
7) sin x cos x ;
8) cos x sin x ;
1
9) tg x
;
2
cos x
1
10) ctg x 2 ;
sin x
1
11) ln x .
x

5.

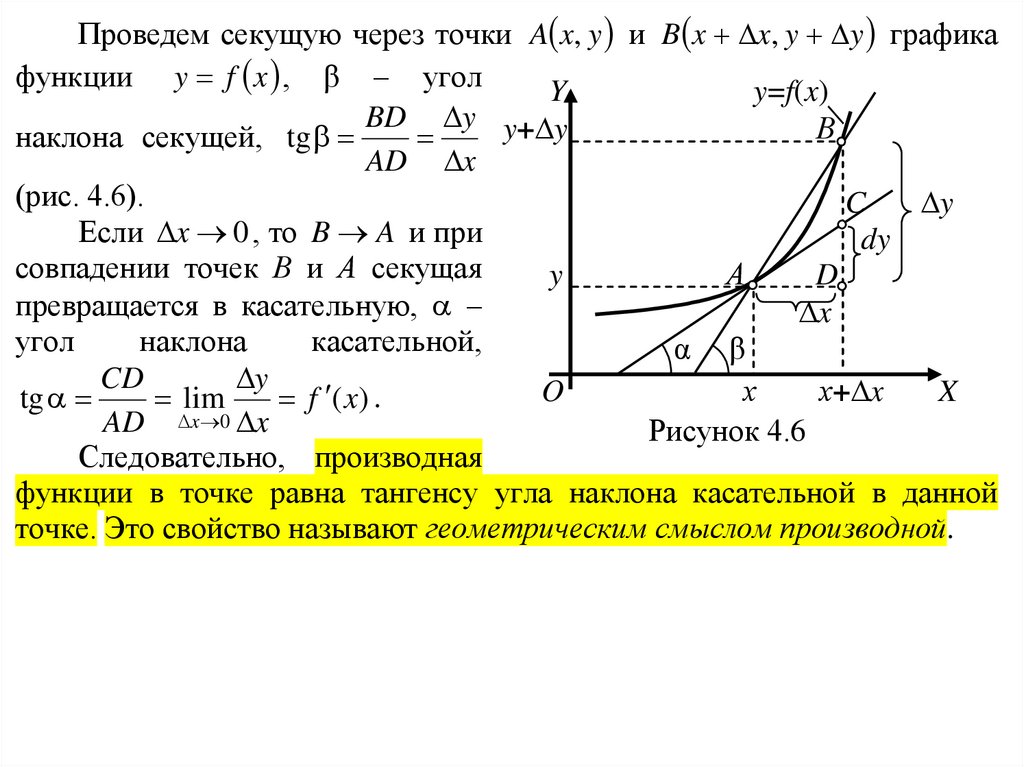
Проведем секущую через точки A x, y и B x x, y y графика
функции y f x , β – угол
Y
y=f(x)
BD y y+ y
В
наклона секущей, tg
AD x
(рис. 4.6).
C
y
Если x 0 , то B A и при
dy
совпадении точек В и А секущая
y
А
D
превращается в касательную, –
x
угол
наклона
касательной,
α β
CD
y
O
х
х+ x
X
tg
lim
f ( x) .
AD x 0 x
Рисунок 4.6
Следовательно, производная
функции в точке равна тангенсу угла наклона касательной в данной
точке. Это свойство называют геометрическим смыслом производной.

6.

Бесконечно малой величиной (б.м.в.) называют величину, предел
которой равен нулю.
Если приращение функции y f x можно представить в виде
y A x , где коэффициент A не зависит x, бесконечно малая
более высокого порядка, чем x т.е. lim
0 , то выражение A x
x 0 x
называют дифференциалом функции y f x и обозначают dy или
df x . При этом оказывается, что A f (x ) , т.е. можно написать:
dy f ( x) x .
Если y x , то d x 1 x , т.е. можно обозначать x dx . Из рисунка 4.6
видно, что dy f ( x ) x CD . Следовательно, дифференциал функции
равен приращению ординаты касательной. Это свойство называют
геометрическим смыслом дифференциала.
Пример. Найти дифференциал функции y x 2 .
2
2
Имеем y x x x 2 2 x x x . Коэффициент 2x не
зависит от x, x 2 бесконечно малая более высокого порядка, чем x
2
x
так как lim
, следовательно dy d x 2 2 x x .
lim
x
0
x 0 x
x 0

7.

Теорема. Если функция u x имеет производную u x в точке x, а
функция y f u имеет производную y u в соответствующей точке
u x , то сложная функция y f x имеет производную y x в точке
x, которая находится по формуле y x yu u x .
Пример. Найти y x , если y ln sin x . Положим u sin x ,
1
1
y x yu u x ln u u sin x x cos x
cos x ctg x .
u
sin x
Теорема. Если функция y f x строго монотонная на интервале
a; b и имеет неравную нулю производную f x в произвольной точке
этого интервала, то обратная функция x y также имеет
производную y в соответствующей точке, определяемой равенством
1
y .
f x
Пример.
Найти
производную
y x ,
пользуясь
правилом
дифференцирования обратной функции, для функции y 3 x 5 .

8.

Обратная
функция
Следовательно, имеем y x
x y3 5
имеет
производную
1
1
1
2
.
2
x y 3 y
33 x 5
x y 3y 2 .
Рассмотрим функцию y f u , где u x . Если функции f и u
являются дифференцируемыми, то производная сложной функции
y f x равна f x yu u x . Так как du u x dx , то дифференциал
функции y равен
dy f x dx yu u x dx yu du f u du ,
т.е. формула дифференциала не изменяется, если вместо функции от
переменной x рассматривать функцию от переменной u. Это свойство
дифференциала
называют инвариантностью
формы
первого
дифференциала.

9.

f x 0
f x
или lim
и функции
x x0 g x
x x0 g x
0
f x и g x дифференцируемы в окрестности точки x0, то
f x
f x
lim
lim
.
x x0 g x
x x0 g x
3
3
x 1 0
x 1
3x 2
3 3
Пример. lim 4
lim
lim 3 lim .
x 1 x 1
x 1 4 x
0 x 1 x 4 1 x 1 4 x
4
Если функция y f x имеет производную в каждой точке x своей
области определения, то ее производная f x есть функция от x.
Функция f x , в свою очередь, может иметь производную, которую
называют производной второго порядка функции y f x (или второй
производной) и обозначают символом f x . Таким образом
f x f x0
d2y
f x x f x
f x 2 lim
lim
f x .
x x0
x 0
x x0
x
dx
В общем случае производная n-го порядка функции y f x есть первая
производная от производной n 1 -го порядка этой функции:
dny
n
n 1
x .
f x n f
dx
Правило Лопиталя. Если lim

10.

Пример. Найти все производные функции f x x 3 . Имеем
f x 3x 2 , f x 6 x, f x 6, f IV x 0 .
Пусть
функция y f x зависит
от
переменной
xи
дифференцируема в точке x. Если в точке x дифференциал dy f x dx
есть дифференцируемая функция от x, то существует дифференциал от
дифференциала
функции,
который
называют
d dy данной
дифференциалом второго порядка функции y f x и обозначают:
d 2 y d dy .
В
общем
случае
дифференциалом n-го
порядка
d n y функции y f x называют дифференциал от дифференциала
n 1 -го порядка этой функции:
d n y d d n 1 y .
Пусть y f x функция независимой переменной x, имеющая
дифференциалы любого порядка. Первый дифференциал функции
y f x равен
dy f x dx ,
где dx x не зависит от x. По определению
d 2 y d dy d f x dx .

11.

Для дифференциала dy величина dx является постоянной и может быть
вынесена за знак дифференциала:
d 2 y d f x dx .
Так как
d f x f x dx f x dx ,
то
2
d 2 y dx dx f x f x dx .
В общем случае дифференциал n-го порядка имеет вид:
d n y f n x dx n .
Отсюда получим
n
d
y
f n x
.
n
dx