Дифференциальное исчисление функций одной переменной

1. Дифференциальное исчисление функций одной переменной

Определение производной. Ее геометрический и
физический смысл.
Связь между непрерывностью и
дифференцируемостью функции. Необходимое
условие существования производной.
Правило дифференциорания функций.
Производная сложной и обратной функции.
Производные основных элементарных функций.
Дифференцирование неявных и параметрически
заданных функций.
Производные высших порядков.
Дифференциал функции. Свойства дифференциала.

2. Приращение функции и аргумента

y f ( x)
Пусть функция
определена на
промежутке X. Рассмотрим точку x X
Разность x 0 называется приращением
аргумента x.
Разность y f ( x x) f ( x) называется
приращением функции y=f(x) в точке x,
соответствующее приращению аргумента x.
y
f ( x x )
f(x)
y
x
x x x
x

3. Определение производной функции

Производной функции y=f(x) в точке x называется
предел отношения приращения функции к
приращению аргумента, когда приращение
аргумента стремится к нулю.
y
f ( x x) f ( x)
y lim
lim
x 0 x
x 0
x
dy df
y , f ( x ),
,
,y
dx dx
Если функция y=f(x) в точке x имеет конечную производную, то
функция y=f(x) называется дифференцируемой в этой точке.
Функция, дифференцируемая во всех точках промежутка X,
называется дифференцируемой на этом промежутке.

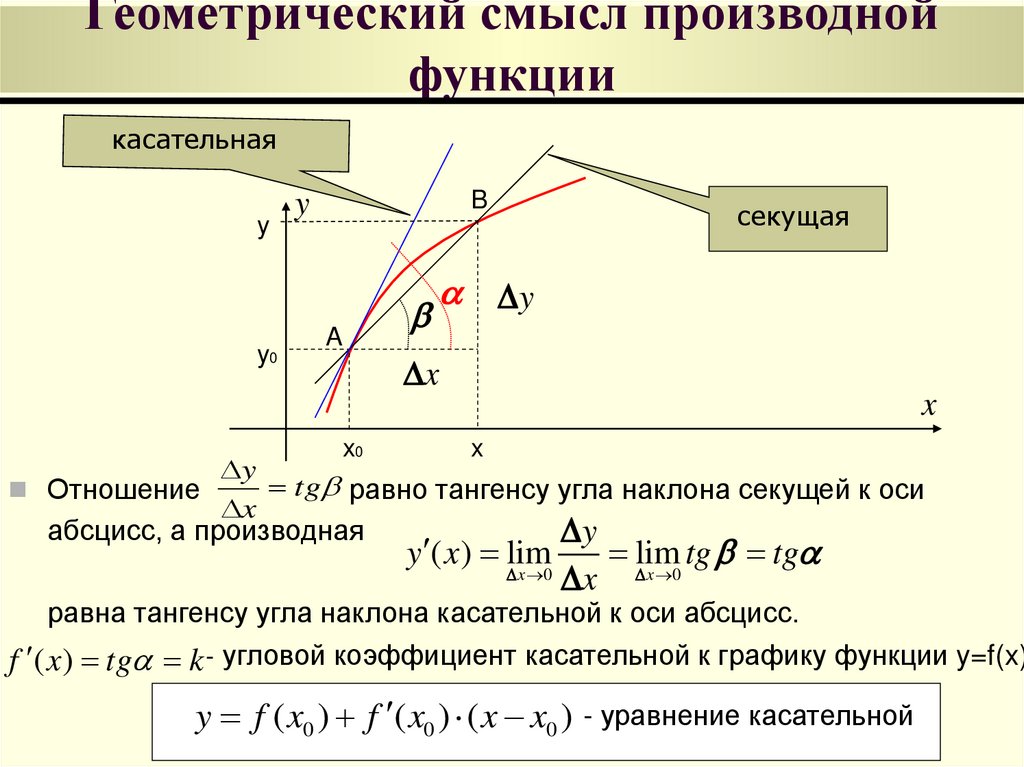
4. Геометрический смысл производной функции

касательная
y
y0
B
y
A
секущая
y
x
x0
x
x
y
tg равно тангенсу угла наклона секущей к оси
x
абсцисс, а производная
y
Отношение
y ( x) lim
x 0
x
lim
tg tg
x 0
равна тангенсу угла наклона касательной к оси абсцисс.
f ( x) tg k - угловой коэффициент касательной к графику функции y=f(x)
y f ( x0 ) f ( x0 ) ( x x0 ) - уравнение касательной

5. Физический смысл производной функции

Если s s (t ) - путь, пройденный материальной
точкой за время, то s s (t t ) s (t ) - путь,
пройденный за время t.
s
s (t ) lim
v
(
t
)
t 0
t
Производная пути
по
времени равна мгновенной скорости в точке t .

6. Связь между непрерывностью и дифференцируемостью функции

(необходимое условие существования производной)
Если функция дифференцируема в некоторой точке,
то она непрерывна в ней.
Пусть функция y=f(x) дифференцируема в некоторой
y
f ( x )
точке x, то есть по определению lim
x 0 x
Тогда по теореме о связи функции, ее предела и
бесконечно малой функции имеем
y
f (x) , где 0при x 0
x
y 0
y f ( x) x x lim
x 0
lim y 0 функция y=f(x) непрерывна в точке x
x 0

7. Связь между непрерывностью и дифференцируемостью функции

Теорема обратная необходимому условию
существования производной не верна.
x, x 0 - непрерывна в точке x=0,
y x
x, x 0 но не дифференцируема в ней
y
0
x
y f (0 x) f (0) f ( x)
x
x
x
x 1, x 0
y
не lim
x 0 x
x 1, x 0
Т.о. функция y x не имеет производной в точке x=0

8. Правила дифференцирования функций

Производная постоянной равна нулю: с 0, с const
Если функции u ( x), v( x) имеют производные в точке
x , то их сумма u ( x) v( x) , произведение u ( x) v( x)
u ( x)
, v( x) 0 также имеют производные в
и частное
v( x)
этой точке и справедливы формулы
(u v ) u v
(u v ) u v u v
u v uv
u
2
v
v
(сu ) cu

9. Правила дифференцирования функций

u
u v uv
( )
v
v2
u
y
v
u ( x x) u ( x)
u ( x x) v( x) u ( x) v( x x)
v( x x) v( x)
y lim
lim
x 0
x
0
x
v( x) v( x x) x
u ( x x) v( x) u ( x) v( x) (u ( x) v( x x) u ( x) v( x))
x 0
v( x) v( x x) x
lim
1
(u ( x x) u ( x)) v( x) (v( x x) v( x)) u ( x)
lim
2
x
0
v ( x)
x
1
u ( x x) u ( x)
v( x x) v( x)
2
(v( x) lim
u ( x) lim
)
x
0
x
0
v ( x)
x
x
1
u v u v
2
(u ( x) v( x) u ( x) v ( x))
v ( x)
v2

10. Производная сложной функции

(о производной сложной функции)
Если y=f(u) и u=h(x) дифференцируемые функции от
своих аргументов, то производная сложной функции
y=f(h(x)) существует и равна
y ( f (h( x))) f (h( x)) h ( x) или y x yu u x
1. y cos x
2
y (cos 2 x) 2 cos x ( sin x) sin 2 x
1
2. y
ln( x 2 1)
1
2x
2
1
2
2
y ((ln( x 1)) ) 1 (ln( x 1)) 2 2 x 2
x 1
( x 1) ln 2 ( x 2 1)

11. Производная обратной функции

(о производной обратной функции)
Если функция y=f(x) строго монотонна на интервале
(a,b) и имеет неравную нулю производную f (x ) в
произвольной точке этого интервала, то обратная ей
функция x=h(y) также имеет производную h ( y ) ,
определяемую h ( x) 1 или x 1
y
f ( x)
y x
y 3 x 1
3
3
2
x y 1
x y ( y 1) y 3 y
1
1
1
1
x y
y x
2 3
y x
x y 3 y
3( x 1) 2

12. Производные основных элементарных функций

1
,
x
c 0, c const
(ln x )
( x ) x 1
(arcsin x )
( a x ) a x ln a
(arccos x )
( e x ) e x
( arctgx )
(sin x ) cos x
(cos x ) sin x
1
(tgx )
cos 2 x
1
(ctgx )
sin 2 x
(log a x )
log a e
,
x
1
1 x2
1
1 x2
1
1 x2
1
( arcctgx )
1 x2
( shx) chx
(chx) shx
(thx )
1
ch 2 x
(cthx )
1
sh 2 x

13. Производные основных элементарных функций

x x
ln(
)
y
ln( x x) ln x
x
(ln x) lim
lim
lim
x 0 x
x 0
x 0
x
x
x
x
ln( 1
)
1
1
x
x
lim
lim
lim
x 0
x 0 x
x 0 x
x
x
1
(ln x )
x
2.
ln x
1
1
(log a x) (
)
(ln x)
ln a
ln a
x ln a
1
(log a x)
x ln a
1.

14. Дифференцирование неявно заданных функций

F(x,y)=0
Для нахождения производной достаточно
продифференцировать уравнение F(x,y)=0 по х, рассматривая
при этом y как сложную функцию x и затем полученное
уравнение разрешить относительно
y
1. y 2 x cos y 1 0
y 2 sin y y 0 y
2
1 sin y
2. x 3 y 3 3xy 0
2
y x
2
2
3 x 3 y y 3 y 3 x y 0 y 2
y x

15. Дифференцирование параметрически заданных функци

x x(t )
, t - параметр
y y (t )
Пусть x(t), y(t) имеют производную и функция x=x(t) имеет
обратную t=h(x).
1
по правилу дифференцирования обратной функции t x
xt
Функцию y=y(x), определяемую параметрическими
уравнениями, можно рассмотреть как сложную функцию y=y(t),
yt
где t=h(x).
y
по правилу дифференцирования сложной функции
x t
2
y
t
3
x
xt
3t 2
3t
xt 3t 2 , yt 2t y x
2t
2

16. Производные высших порядков

y f (x ) - производная первого порядка функции y=f(x)
Если функция f ( x ) дифференцируемой точке x, то
y ( f ( x )) - производная второго порядка функции y=f(x)
d 2 y d dy
y , f ( x),
,
(
)
2
dx
dx dx
…………………………………….
y ( n ) ( f ( n 1) ( x)) - производная n-ого порядка функции y=f(x)
Производные порядка выше первого называются
производными высших порядков.

17. Понятие дифференциала функции

Пусть функция y=f(x) определена на промежутке X и
дифференцируема в некоторой окрестности точки
x X.
y
lim
f ( x ) 0
x 0 x
По теореме о связи между функцией, ее пределом и б. м. ф.
y
f ( x ) ( x ),где lim ( x) 0
x
x 0
y f ( x ) x ( x) x
f ( x) x
lim
f ( x) 0
x 0
x
lim
x 0
( x) x
x
f ( x) x является б.м. функцией
одного порядка с x
является б.м. функцией
(
x
)
x
lim ( x) 0
x 0
более высокого порядка порядка чем x

18. Понятие дифференциала функции

Дифференциалом функции y=f(x) называется главная,
линейная относительно x , часть приращения функции,
равная произведению производной функции на приращение
независимой переменной
dy f ( x) x
dy – дифференциал первого порядка
Рассмотрим функцию y=x. Вычислим ее дифференциал:
dy x x 1 x x dy x
dy f ( x ) dx
Дифференциалом функции y=f(x) равен произведению
производной этой функции на дифференциал независимой
переменной

19. Найти дифференциал функции

f ( x) 3x sin( 1 2 x)
2
dy f ( x) dx
dy (3x sin( 1 2 x)) dx
2
dy (6 x 2 cos(1 2 x)) dx

20. Свойства дифференциала

Дифференциал постоянной равен нулю:
dс 0, с const
d (u v) du dv
d (u v) vdu udv
vdu udv
u
d
2
v
v
d (с u ) c du