Похожие презентации:
Кеңістіктегі түзу мен жазықтықтың өзара орналасуы_Презентация
1. Кеңістіктегі түзу мен жазықтықтың өзара орналасуы
2.
Оқу мақсаты:11.2.6 - кеңістіктегі түзу мен жазықтықтың
өзара орналысуын білу
Сабақ мақсаты:
кеңістіктегі түзу мен жазықтықтың өзара орналасу
жағдайларын қарастыру;
кеңістіктегі түзу мен жазықтықтың өзара орналасуын
анықтауға есептер шығару.
3. Түзудің канондық теңдеуі
q m; n; pL птүзуі М0(x0; y0; z0) арқылы өтіп
Векторына параллель болсын:
Онда М (x; y; z) нүктесі жазықтыққа тиісті тиісті
болады егер
q m; n; pжәне
q
L
М0
М
M M x x ; y y ; z z
0
0
0
векторлары коллинеар болса
0
Екі түзудің коллинеарлық шарты:
x x0 y y 0 z z0
m
n
p
Түзудің канондық теңдеуі
q m; n; p
- Бағыттаушы вектор
4. Екі нүкте арқылы өтетін түзудің теңдеуі
Түзуі М1(х1; у1 ; z1 ) және М2(х2; у2 ; z2 ). арқылы өтетін болсынq
М2
L
М1
Онда түзудің канондық теңдеуіне
бағыттаушы вектор ретінде келесі
векторды алуға болады.
q M1M 2 x 2 x1; y 2 y 1; z2 z1
x x1
y y 1 z z1
y 2 n y1 z2 p z1
mx1
x2
Екі нүкте арқылы өтетін
түзудің теңдеуі
5. Түзудің параметрлік теңдеуі
Түзідің канондық теңдеуінен түзудің параметрлік теңдеуін аламыз:x x0 y y 0 z z0
t
m
n
p
x mt x0
y nt y 0
z pt z
0
x x0
m t
y y
0
t
n
z z0 t
p
Түзудің параметрлік теңдеуі
6. Жазықтықтың жалпы теңдеуі
x , y және z үш белгісізді бірінші дәрежелі теңдеудіқарастырайық:
Ax By Cz D 0
(1)
М0(x0; y0; z0) жазықтықта жатсын:
Ax0 By 0 Cz0 D 0
(2)
(1) теңдеуден (2) теңдеуді алып тастайық:
A x x0 B y y 0 C z z0 0
Жазықтықтың жалпы теңдеуі
(3)
7.
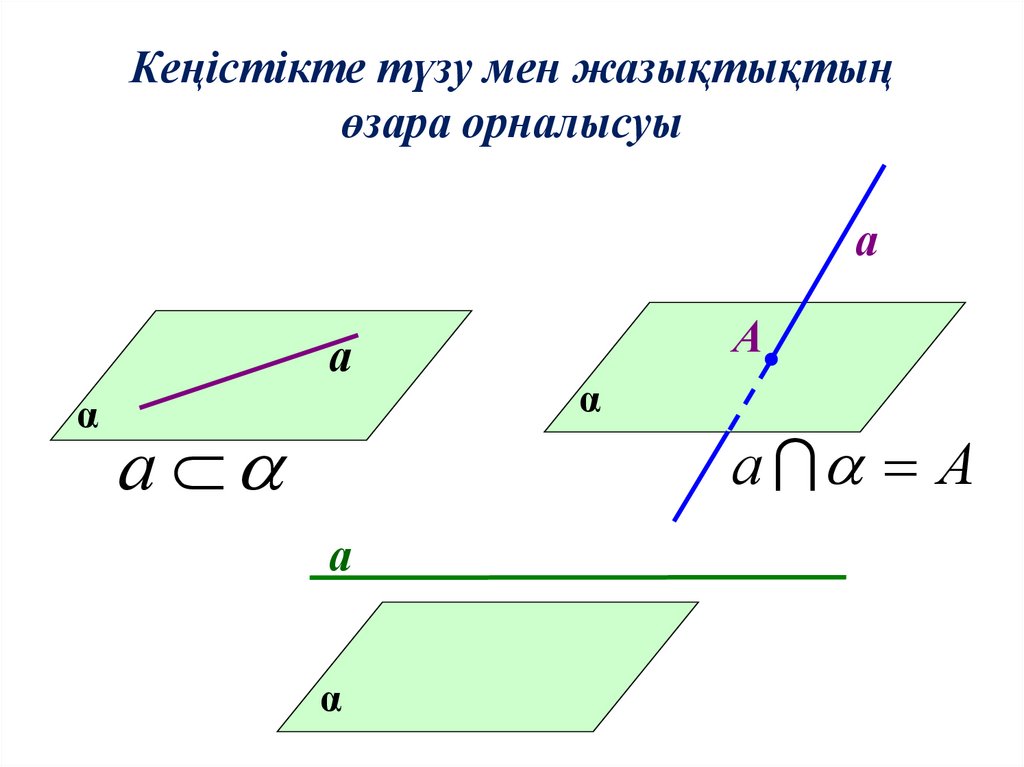
Жазықтықтың жалпы теңдеуі8. Кеңістікте түзу мен жазықтықтың өзара орналысуы
аа
α
а
а
α
А
α
а А
9. Кеңістікте түзу мен жазықтықтың өзара орналысуы
Кеңістікте λ жазықтығы мен ℓ түзуі берілген.Жазықтық пен түзудің орналасуы:
1) параллель;
2) түзу жазықтықтың бойында орналасқан;
3) түзу мен жазықтық бір нүктеде қиылысады.
λ: Ax + By + Cz + D = 0
x x0 y y0 z z0
,
және :
m
n
p
онда N̄= {A; B; C} – λ жазықтықтың нормаль векторы,
{m; n; p}
– ℓ түзудің бағыттаушы векторы болады.
10.
NN
N
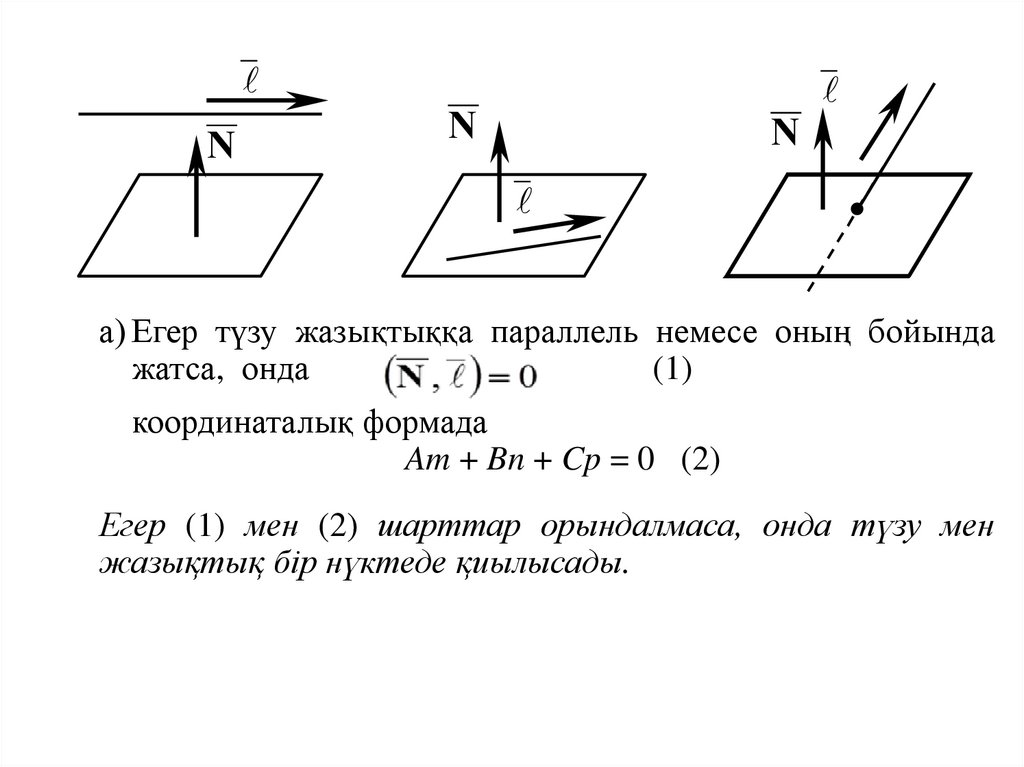
а) Егер түзу жазықтыққа параллель немесе оның бойында
жатса, онда
(1)
координаталық формада
Am + Bn + Cp = 0 (2)
Егер (1) мен (2) шарттар орындалмаса, онда түзу мен
жазықтық бір нүктеде қиылысады.
11.
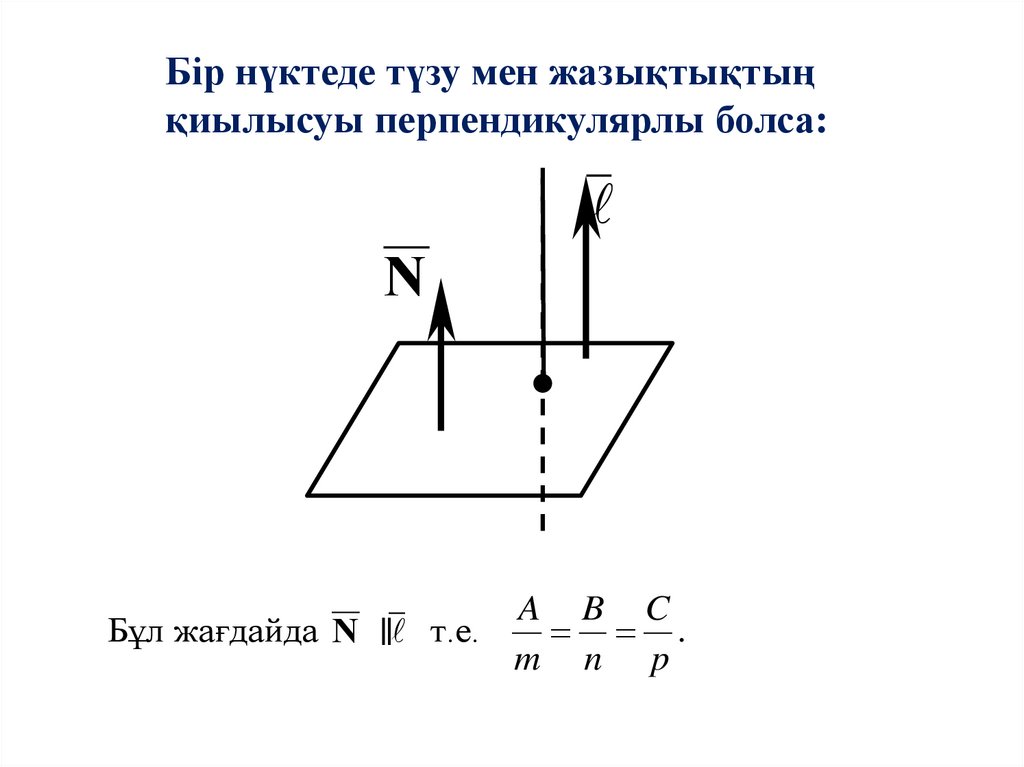
Бір нүктеде түзу мен жазықтықтыңқиылысуы перпендикулярлы болса:
N
A B C
Бұл жағдайда N т.е.
.
m n p
12. Түзумен жазықтықтың қиылысу нүктесі
Жазықтық теңдеундегі x; y; z орына қойып :A(mt x0 ) B(nt y 0 ) C( pt z0 ) D 0
t-ға қатысты теңдеуді шешеміз:
Ax0 By 0 Cz0 D
t0
Am Bn Cp
t0 мәнін түзудің параметрлік теңдеуге қоямыз:
xK mt0 x0
y K nt 0 y 0
z pt z
0
0
K
K ( xK ; y K ; zK )
13. Мысал
Түзу мен жазықтықтың қиылысу нүктесін табыңдарx 1 y z 2
3
5
1
y 5z 6 0
Түзудің парметрлік теңдеуін жазамыз:
Жазықтық теңдеуіне қоямыз:
5t 5(t 2) 6 0
x 3t 1
y 5t
z t 2
10t 16 0 t 0 1.6
Түзудің теңдеуіне қоямыз:
x 3 ( 1.6) 1
y 5 ( 1.6)
z 1.6 2
x 3 . 8
y 8
z 0 .4
K ( 3.8; 8; 0.4)
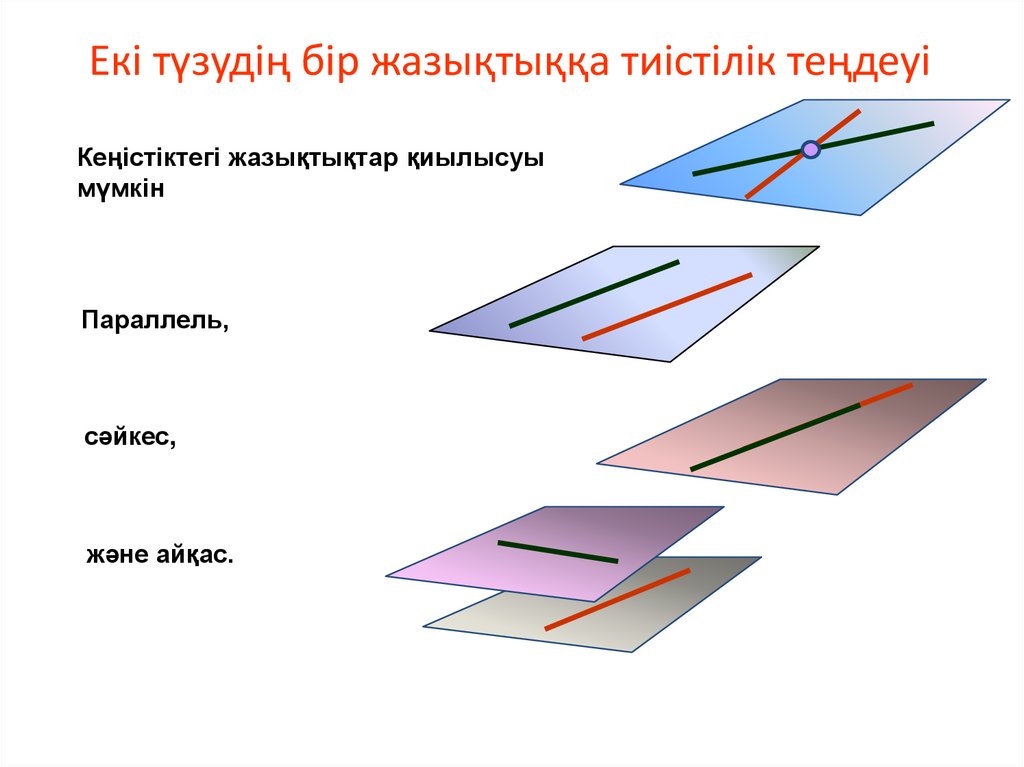
14. Екі түзудің бір жазықтыққа тиістілік теңдеуі
Кеңістіктегі жазықтықтар қиылысуымүмкін
Параллель,
сәйкес,
және айқас.
15. Тапсырма 1.
А – ның қандай мәніндетүзу жазықтыққа параллель болады
16. Тапсырма 2.
В және n қандай мәндеріндетүзу мен жазықтық перпендикуляр болады
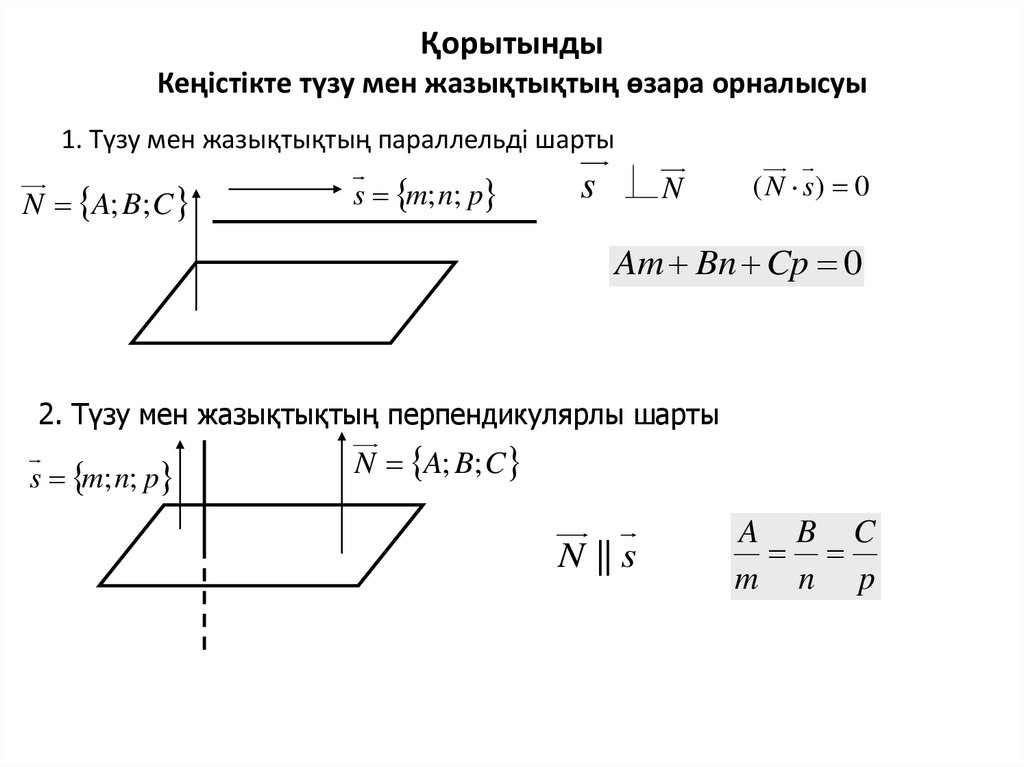
17. Қорытынды Кеңістікте түзу мен жазықтықтың өзара орналысуы
1. Түзу мен жазықтықтың параллельді шартыN A; B; C
s m; n; p
s
N
( N s) 0
Am Bn Cp 0
2. Түзу мен жазықтықтың перпендикулярлы шарты
s m; n; p
N A; B; C
N || s
A B C
m n p
18.
Рефлексия- нені білдім, нені үйрендім?
- нені толық түсінбедім?
- немен жұмысты жалғастыру қажет?













 Математика
Математика








