L_16

1. Опр. Ф. y = f(x) называется непрерывной справа в x0, если ∃ правосторонний предел и

Уже написали
§ 5. Непрерывность функций
Опр. Ф. y = f(x) называется непрерывной справа в x0, если
∃ правосторонний предел и
lim f ( x) f ( x0 )
x x 0
Ф. y = f(x) называется непрерывной слева в x0, если
∃ левосторонний предел и
lim f ( x) f ( x0 )
x x 0
Опр
y = f(x) называется непрерывной в x0, если
lim f ( x) lim f ( x) f ( x0 )
x x 0
Опр
x x 0
y = f(x) называется непрерывной в x0, если
lim D y . 0
D x 0
Б. м. приращению аргумента Dx = x – x0 соответствует б. м. приращение
функции
D y = f ( x ) – f ( x0 )

2.

Уже написали
Общие свойства непрерывных функций
1. Всякая основная элементарная функция непрерывна в своей области
определения.
Доказать для каждой
пропустить 5 клеточек
2. Сумма, произведение, частное непрерывных на (a,b) функций есть
непрерывная на (a,b) функция
3. Непрерывность композиции элементарных функций.
Если
u = j ( x ) – непрерывна в x0
y = f ( u ) – непрерывна в u0
то сложная функция y = f ( j ( x )) непрерывна в x0
Следствие. Операция предельного перехода перестановочна.
lim f (u) f ( lim u( x) )
u u 0
пропустить 10 клеточек
x x 0

3.

Это новое
Точки разрыва и их классификация
Опр. Т. x0 называется точкой разрыва ф. y = f(x), если для нее не
выполняется определение непрерывности.
lim f ( x) f ( x0 )
x x 0
Т.
x0 - точка устранимого разрыва, если ∃ lim f ( x)
но
x x 0
lim f ( x) f ( x0 )
x x 0
Т. x0 - точка скачка (разрыв I рода), если
lim f ( x) A
x x 0
4х4
клетки
lim f ( x) B
x x 0
Т. x0 - точка разрыва I I рода, если
хотя бы один из односторонних пределов
и
4х4
клетки
A B
∞
или
∄.
4х4
клетки

4. План исследования функции на непрерывность

1. Найти точки, подозрительные на разрыв
2. Найти lim f ( x) и lim f ( x). Вычислить f (x0)
x x 0
x x 0
3. Назвать характер разрыва
4. Построить график. (При необходимость вычислить
пропустить 1 страницу
lim f ( x) ).
x

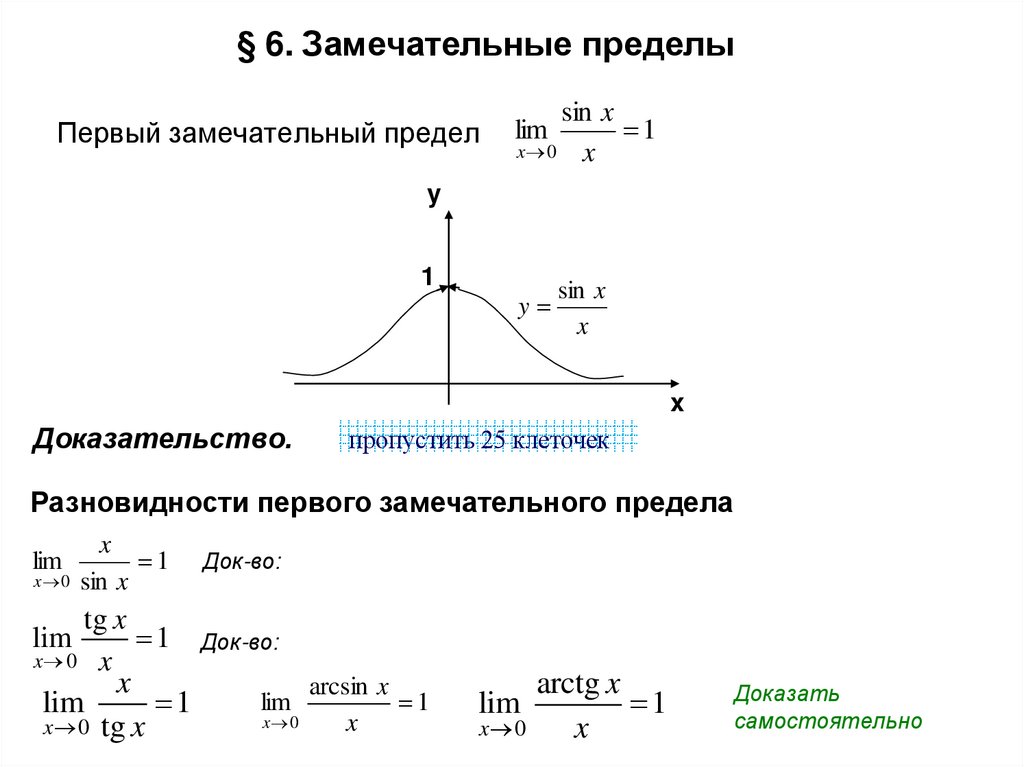
5. Первый замечательный предел

§ 6. Замечательные пределы
Первый замечательный предел
sin x
1
x 0 x
lim
y
1
y
sin x
x
x
Доказательство.
пропустить 25 клеточек
Разновидности первого замечательного предела
x
1
x 0 sin x
lim
Док-во:
tg x
1 Док-во:
x 0 x
x
arcsin x
lim
1
lim
1
x
0
x
x 0 tg x
lim
arctg x
lim
1
x 0
x
Доказать
самостоятельно

6.

x
1
lim 1 e
Второй замечательный предел
x
x
Некоторые замечательные следствия
log a (1 x)
x 0
x
1
log a (1 x)
lim
x 0
ln a
x
ax 1
lim
ln a
x 0
x
3.
lim
x 0
оставить пустую строку для вывода
1. lim
ax 1
2. lim
x 0
x
1
1 x x e
в частности
ln( 1 x)
1
x 0
x
lim
оставить пустую строку для вывода
в частности
ex 1
lim
1
x 0
x
(1 x) 1
lim
x 0
x
Несуществующие пределы lim sin x
x
lim sin
x 0
1
x
lim ( 1) n
n

7.

Эквивалентные бесконечно малые и их свойства
Опр. Бесконечно малые a ( x ) и b ( x ) при x→x0 называются
эквивалентными, если
a( x)
1
x x0 b( x )
Таблица эквивалентных б.м.
lim
0
1. sin a a
a
a2
a 0
2. 1 cosa
2
a 0
3. tg a
a
0
4. arcsin a a
a
a 0
5. arctg a
a
a 0
6. ea 1
a
Пишут a ( x ) ~ b ( x )
ВЫУЧИТЬ!
a 0
6*. aa 1
a ln a
0
7. ln(1 a ) a
a
a 0
7 *. logb (1 a)
a
ln b
a 0
8. (1 a) 1
a
пропустить 15 клеточек

8. Пусть a ( x ) и b ( x ) б.м.ф. при x → x0. Рассмотрим

§ 7. Сравнение бесконечно малых
Пусть a ( x ) и b ( x ) б.м.ф. при x → x0. Рассмотрим
Опр. a ( x ) и b ( x ) – б.м. одного порядка малости, если
a( x )
lim
A 0
x x0 b( x)
a ( x)
x x 0 b ( x )
lim
Опр. a ( x ) – б.м. высшего порядка малости относительно b ( x ), если
a( x)
lim
0
x x0 b( x)
пишут: a ( x ) = o (b ( x )) или a ( x ) << b ( x )
Опр. a ( x ) – б.м. низшего порядка малости относительно b ( x ), если
a( x)
lim
x x0 b( x)
пишут: b ( x ) = o (a ( x )) или b ( x ) << a ( x )
a( x)
, то a ( x ) и b ( x ) не сравнимы между собой
Опр. Если lim
x x0 b( x)
пропустить 15 клеточек

9.

Свойства эквивалентных бесконечно малых
1. Если a ( x ) ~ b ( x ) и b ( x ) ~ g ( x ) то a ( x ) ~ g ( x ) при x→x0
пропустить 6 клеточек
2. Сумма б.м. величин разного порядка малости эквивалентна слагаемому
низшего порядка малости.
пропустить 30 клеточек
3. При вычислении пределов произведения и частного б.м. величины
можно заменять их эквивалентами.
пропустить 15 клеточек
4. Произведение б.м. a ( x ) и b ( x ) есть б.м. высшего порядка
малости по сравнению с каждым из сомножителей.
a ( x ) b ( x ) << a ( x )
пропустить 5 клеточек
5. Критерий эквивалентности двух б.м.
Пусть a ( x ) и b ( x ) – б.м. при x→x0.
a ( x ) ~ b ( x ) ⇔ a ( x ) – b ( x ) = o( a ( x ) ) или o( b ( x ))
пропустить 30 клеточек

10.

Опр. Пусть a ( x ) и b ( x ) – б.м. при x → x0.
a ( x ) называется б.м. k - го порядка малости относительно b ( x ), если
0 k 1 a b
a( x)
lim k
A 0: 1 k a b
x x0 b ( x )
k 1 a и b одного порядком малости
Число k называется порядком малости
пропустить 20 клеточек

11. Опр. Пусть f ( x ) и g ( x ) б.б.ф. при x → x0. Рассмотрим

Сравнение бесконечно больших функций. Эквивалентные
бесконечно большие
f ( x)
Опр. Пусть f ( x ) и g ( x ) б.б.ф. при x → x0. Рассмотрим
lim
x x 0 g ( x )
1. Б.б. f ( x ) и g ( x ) при x→x0 называются б.б. одного порядка
роста, если
f ( x)
A 0
x x0 g ( x)
lim
2. Б.б. f ( x ) – низшего порядка роста относительно g ( x ), если
f ( x)
0
x x0 g ( x )
lim
пишут: f ( x ) << g ( x )
3. Б.б. f ( x ) – б.б. высшего порядка роста относительно g ( x ), если
f ( x)
x x0 g ( x )
lim
пишут: f ( x ) >> g ( x )
4. Б.б. f ( x ) и g ( x ) при x→x0 называются эквивалентными, если
пишут: f ( x ) ~ g ( x )
f ( x)
1
x x0 g ( x)
lim

12.

Свойства
1. Сумма б.б. величин разных порядков эквивалентна слагаемому
высшего порядка роста.
Доказать самостоятельно
2. При вычислении пределов произведения и частного б.б. величины
можно заменять их эквивалентами.
Доказать самостоятельно
3. Произведение двух б.б.ф. имеет высший порядок роста
относительно каждого из сомножителей
Доказать самостоятельно

13.

§ 8. Свойства непрерывных на отрезке функций.
Опр. Функция, определенная на отрезке [ a, b ] и непрерывная в каждой
его точке, называется непрерывной на этом отрезке.
Свойства
Т. 1. (теорема Вейерштрасса об ограниченности и достижении непрерывных на отрезке
функций своих точных границ)
Всякая непрерывная на отрезке функция ограничена и достигает на нем
своих точных верхней и нижней границы
пропустить 10 клеточек
Т. 2. (теорема Коши о промежуточном значении)
Пусть f ( x ) непрерывна на [ a, b ] и на концах отрезка f ( a ) ≠ f ( b ).
Тогда ∀C ∈ [ f ( a ), f ( b ) ] найдется хотя бы одна точка x ∈ [ a, b ] такая,
что f ( x ) = C.
Т. 3. (об обращении непрерывной функции в ноль)
Если функция f ( x ) непрерывна на [ a, b ] и на его концах принимает
значения разных знаков, то на [ a, b ] существует хотя бы одна точка x = x, в
которой f ( x ) обращается в ноль.