Ограниченность функции, имеющей предел

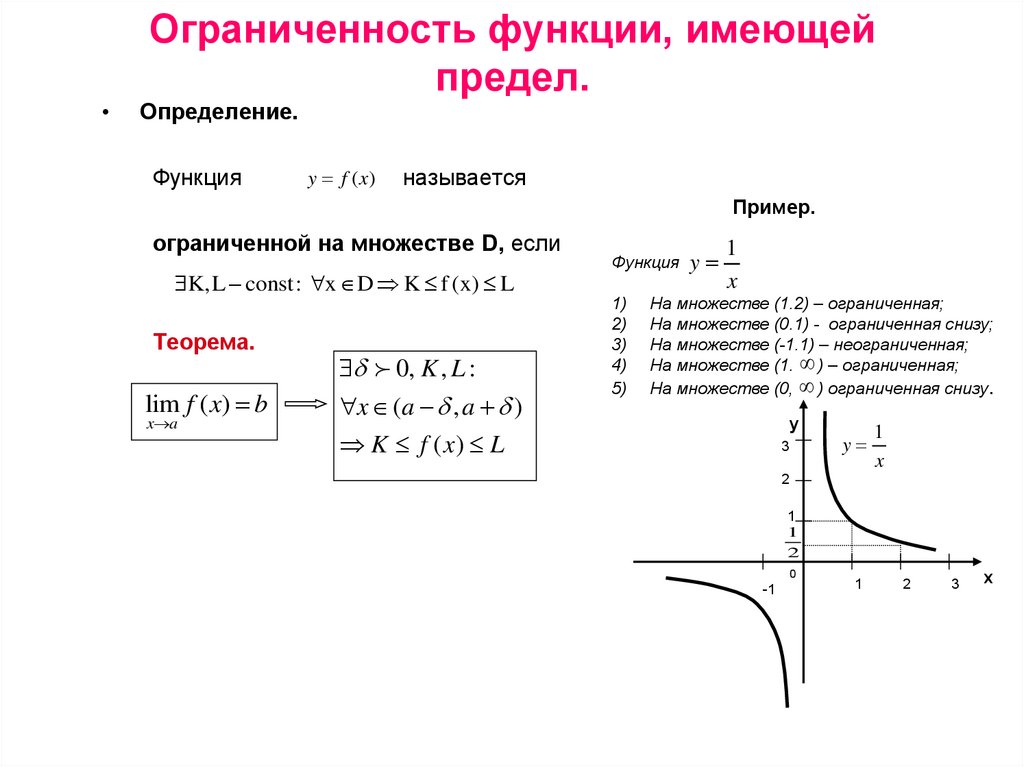
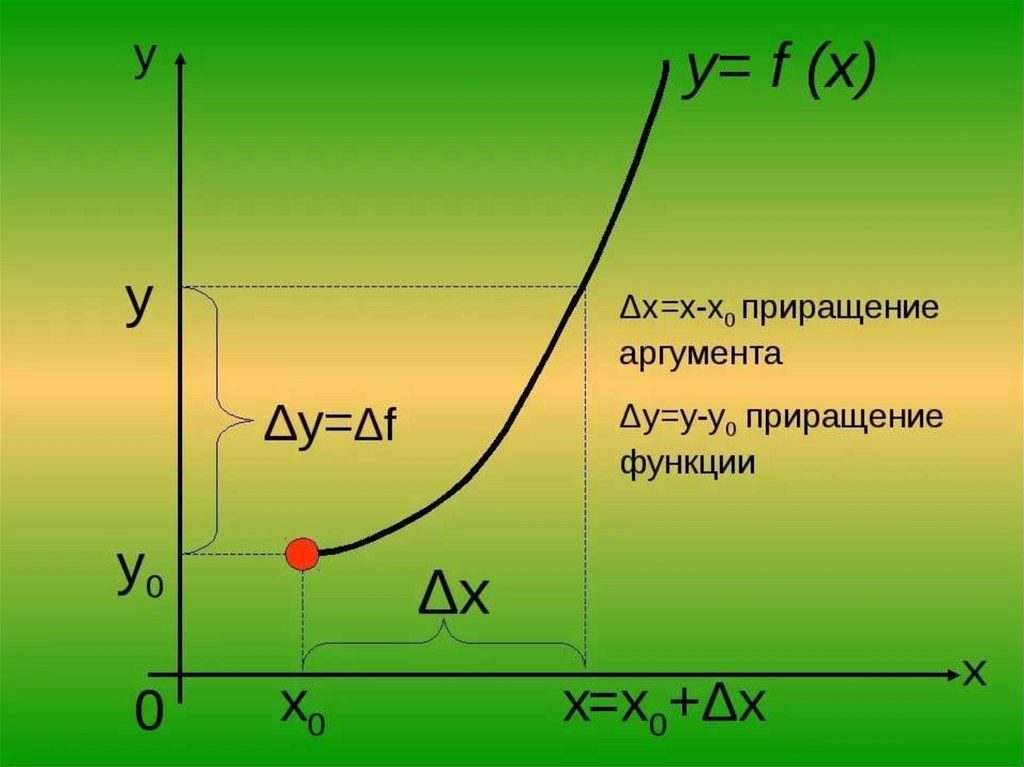
1. Ограниченность функции, имеющей предел.

Определение.
Функция
y f (x)
называется
Пример.
ограниченной на множестве D, если
K, L const : x D K f (x) L
Теорема.
lim f ( x) b
x a
0, K , L :
x (a , a )
Функция
1)
2)
3)
4)
5)
y
1
x
На множестве (1.2) – ограниченная;
На множестве (0.1) - ограниченная снизу;
На множестве (-1.1) – неограниченная;
На множестве (1. ) – ограниченная;
На множестве (0, ) ограниченная снизу.
y
K f ( x) L
3
y
1
x
2
1
1
2
0
-1
1
2
3
х

2.

3. Теорема (о разности между функцией и ее пределом)

f ( x) b ( x)
lim f ( x) b
где (x) - бесконечно малая
при x a
x a
1. Прямая теорема:
–
(необходимость)
lim f ( x) b
x a
2. Обратная теорема:
(достаточность)
f ( x) b ( x)
f ( x) b ( x)
где (x) - бесконечно малая
при x a
где (x) - бесконечно малая
при x a
lim f ( x) b
x a

4.

Доказательство прямой теоремы.
lim f ( x) b 0 ( ) 0 :
x a
x : 0 x a f ( x) b
обозначим: ( x) f ( x) b
( x) lim ( x) 0
x a
Доказательство обратной теоремы.
f ( x) b ( x)
где (x) - бесконечно малая
при x a
0 ( ) 0 :
x : 0 x a ( x)
f ( x) b lim f ( x) b
x a

5. Бесконечно малые величины.(Повторение)

Переменная (x) называется бесконечно малой величиной при x x o , если
0 ( ) 0 :
x : 0 x x o ( x )
То есть
lim ( x ) 0
x x o
Например,
( x ) x 2 , при x 0,
( x ) sin x , при x 0,
( x ) ( x 3) 2 , при x 3,
(x)
2
, при x .
x
(Геометрическую интерпретацию бесконечно малой величины см. ранее, при
определении предела).

6. Основные свойства бесконечно малых величин.

Пусть (x) и (x) - бесконечно малые
при x x
0
x x0
Тогда при
– 1. ( x) ( x) - бесконечно малая
величина.
– 2. ( x) ( x) -бесконечно малая
величина.
3. ( x) f ( x) - бесконечно малая
f (x) ограниченная
величина, если
функция.
Доказательство 1 свойства (для суммы).
1.Обозначим
2.Возьмем число ,где
2
положительное число.
Д.з. Докажите
произвольное
3.Из определения бесконечно малых величин
следует:
свойство 3.
( x) ( x) ( x)
2
2
0 1 0 : x : 0 х х0 1 ( х)
0 2 0 : x : 0 х х0 2 ( х)
2
2
Тогда
0 min( 1 , 2 ) 0 : x : 0 х х 0
( х) ( x) ( x) ( x)

7. СВОЙСТВА ПРЕДЕЛОВ.

Пусть существуют
lim f ( x) a; lim g ( x) b
x xo
x xo
• Тогда:
• 1. lim ( f ( x) g ( x))
x xo
lim f ( x) lim g ( x) a b
x xo
x xo
lim f ( x) g ( x)
x xo
• 2. lim
x xo
Доказательство 1 свойства.
1.
где
(x) и (x)- бесконечно малые при x x0
2.
f ( x) g ( x)
f ( x) lim g ( x) ab
(a b) ( ( x) ( x))
x xo
число
• 3. Если lim g ( x) b 0
x xo
lim f ( x)
f
(
x
)
a
x
xo
то lim
x xo g ( x )
lim g ( x) b
x xo
f ( x) a ( x), g ( x) b ( x),
бесконечно малая
Следовательно
lim ( f ( x) g ( x)) a b
x xo
Д.з. Докажите
свойство 2.

8. Свойства пределов (продолжение)

4. Предел постоянной равен самой постоянной.
5. Постоянной множитель можно выносить за знак
предела.

9. Бесконечно большие величины.

4. Бесконечно большие величины при
lim f ( x)
x xo .
y
x xo
–
–
–
–
Определение.
Функция f (x) называется
бесконечно большой при x x
o
если M 0 ( M ) 0 :
x : 0 x xo
M
0
f ( x) M
Связь бесконечно больших
и бесконечно малых величин.
xo
х
-M
Теорема 1.
Если
то
f (x)- бесконечно большая величина при x xo,
1
- бесконечно малая величина.
f ( x)
1
lim f ( x) lim
0
x xo
x xo f ( x )

10. Пример

2x+5 является бесконечно большой величиной при
x

11.

Теорема 2.
1
lim ( x) 0 lim
x xo
x xo ( x )
Доказательство.
1. Возьмем произвольное
1
и обозначим
M
2. Так как
M 0
lim ( x) 0
,то
x xo
1
0 ( ) 0 :
M
x : 0 x xo ( x)
для
1
1
M
( x)
Следовательно
1
x xo ( x )
lim
Если
то
(x) - бесконечно малая величина при x xo
1
- бесконечно большая величина.
( x)

12.

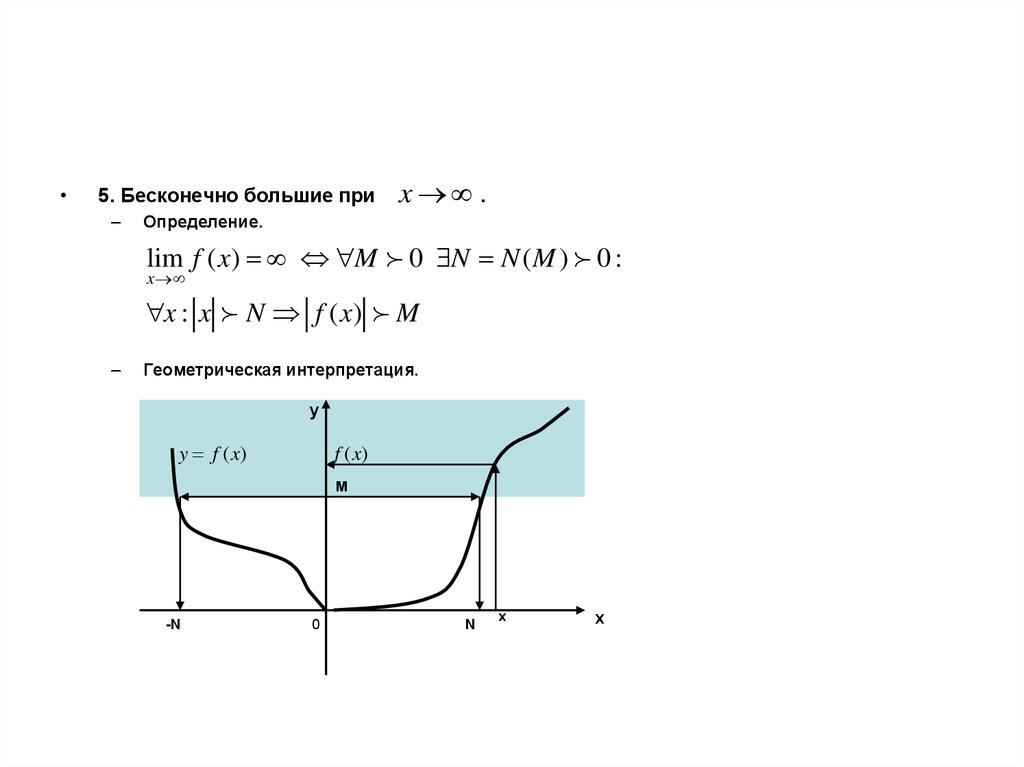
5. Бесконечно большие при
–
x .
Определение.
lim f ( x) M 0 N N ( M ) 0 :
x
x : x N f ( x) M
–
Геометрическая интерпретация.
y
y f (x)
f (x)
M
-N
0
N
х
х

13. Типы неопределенностей

• Вычислить предел
x3 8
(x 2)( x 2 2x 4)
0
lim
lim (x 2 2x 4) 12
xlim
x 2
x 2
0 2 x 2 x 2
• Существуют неопределенности вида
0
, , (0 ), (1 ), ( )
0

14. Признаки существования пределов.

Теорема 1.
Пусть
Теорема 2 (теорема Вейерштрасса).
g1 ( x) f ( x) g 2 ( x);
Пусть
1.
lim g1 ( x) lim g 2 ( x) a
x xo
n : yn M
x xo
lim f ( x) a
lim yn a M
x xo
n
Геометрическая интерпретация.
2.
y
y g 2 ( x)
a
xo
y1 y2 yn
n : yn M
y f (x)
lim yn a M
n
y g1 ( x)
0
y1 y2 yn
х

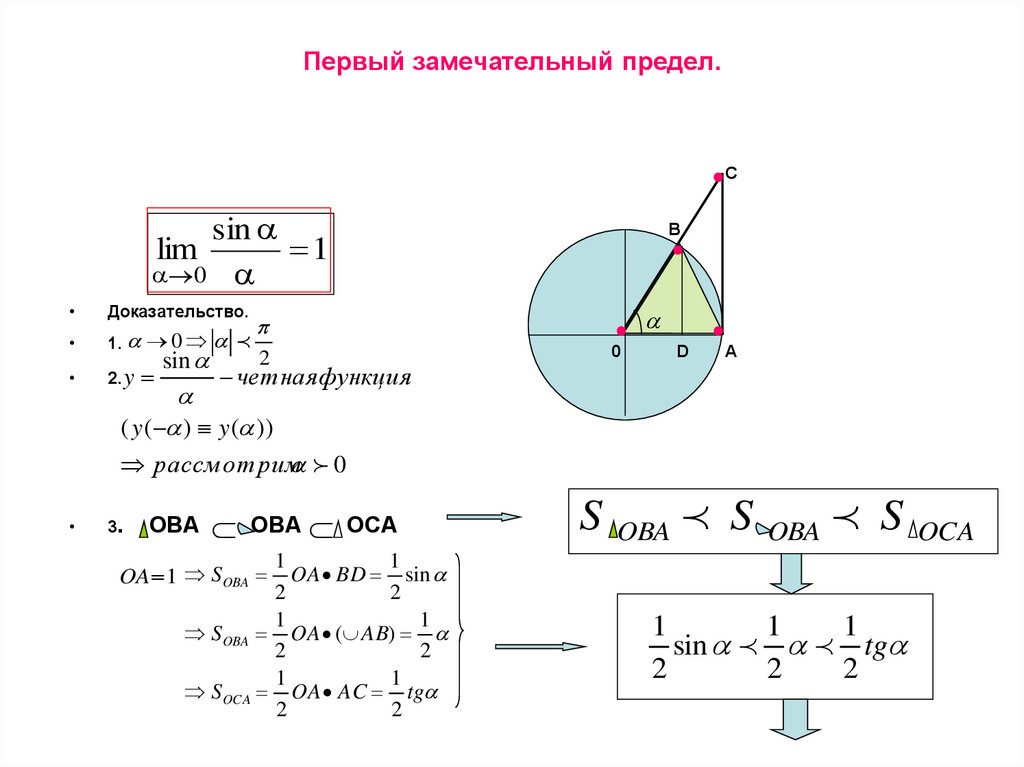
15. Первый замечательный предел.

C
sin
lim
1
0
Доказательство.
1.
2. y
0
sin
B
0
2
чет ная функция
D
A
( y ( ) y ( ))
рассм от рим 0
3.
OBA
OBA OCA
1
1
OA BD sin
2
2
1
1
SOBA OA ( AB)
2
2
1
1
SOCA OA AC tg
2
2
S
OBA
S
OBA
S
OA 1 SOBA
1
1
1
sin tg
2
2
2
OCA

16.

4.
5.
1
1
sin cos
sin tg
0 B A D A OD OA
cos 1
6. По первому признаку существования предела:
lim
0
sin
1
1
sin
cos

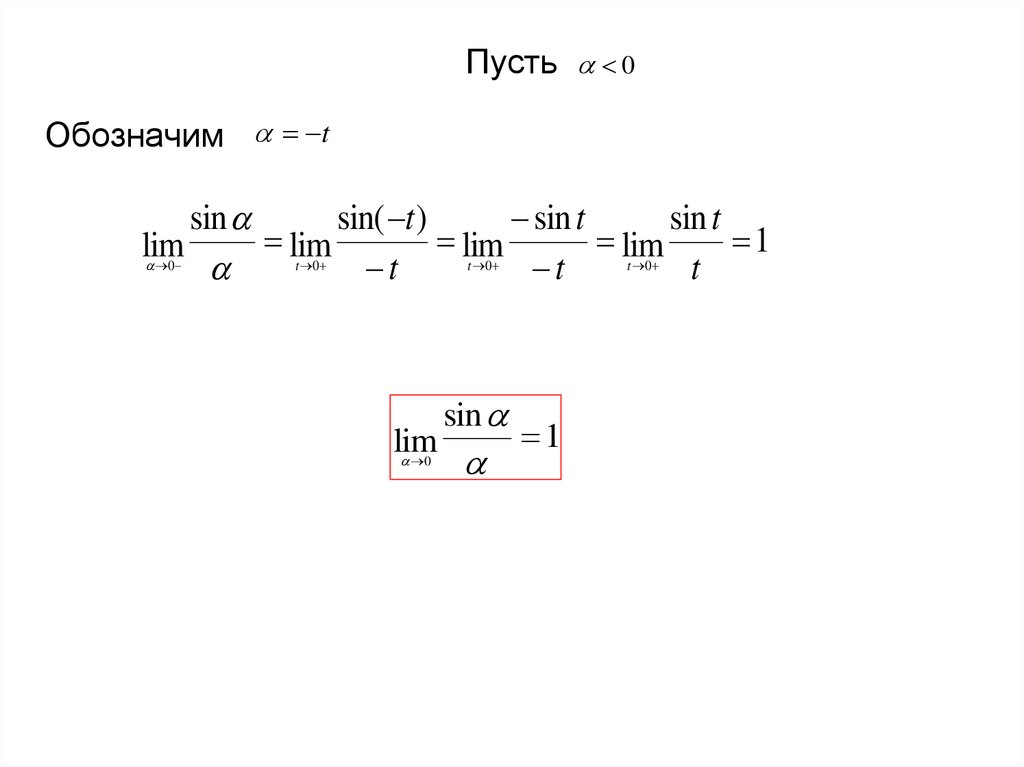
17. Пусть

0
Обозначим t
sin
sin( t )
sin t
sin t
lim
lim
lim
1
lim
t
t
t
0
t 0
t 0
lim
0
sin
t 0
1

18. Второй замечательный предел.

n
1
Lim 1 e
n
n
–
1.
1
an (1 ) n
n
или
1
9
1
64
a1 (1 1)1 2, a2 (1 ) 2 , a3 (1 )3
,
2
4
3
27
–
2. Утверждения:
a1 a2 a3 an
n : an 3
–
3. По второму признаку существования предела:
lim a n
n
1
Lim 1
n
n
n
e
e 2.71828

19. Следствия второго замечательного предела.

x
1
1). Если x – действительное число, то
lim 1 x e ;
x
1
2). lim 1 x x e ;
x 0
a
3). lim 1
x
x
x
ea ;
a
4). lim 1
x
x
bx
e ab ;
5). lim 1 ax
1
x
ea ;
6). lim 1 ax
b
x
e ab ;
x 0
x 0

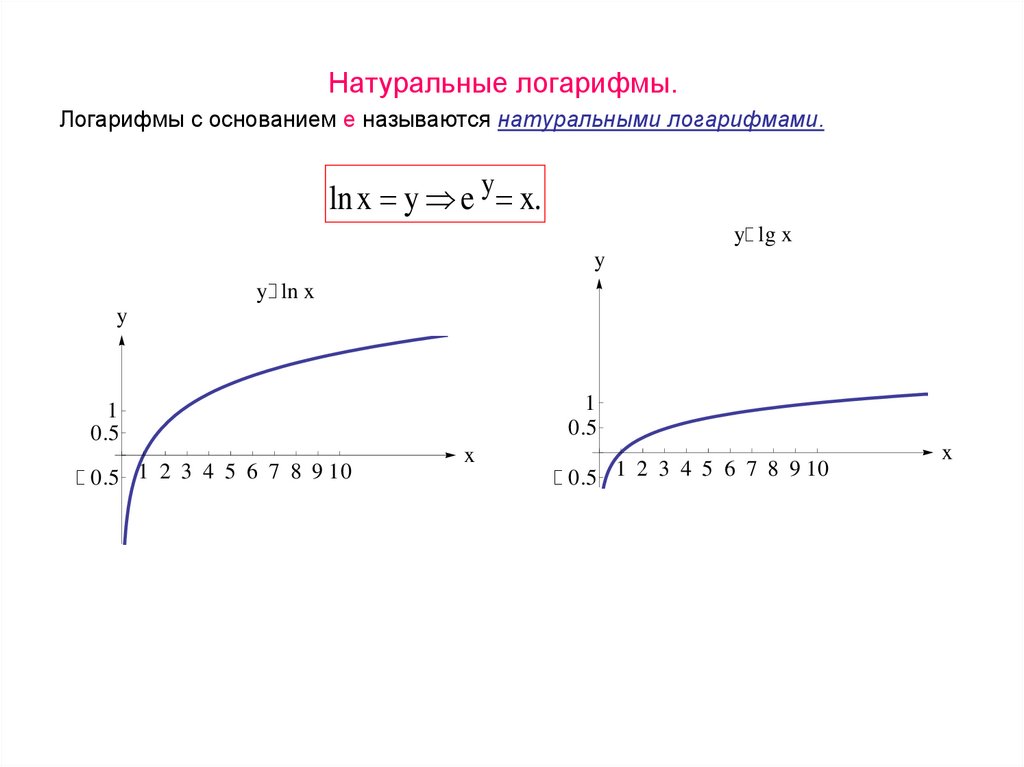
20.

Натуральные логарифмы.
Логарифмы с основанием e называются натуральными логарифмами.
ln x y e y x.
y lg x
y
y ln x
y
1
0.5
1
0.5
0.5 1 2 3 4 5 6 7 8 9 10
x
0.5 1 2 3 4 5 6 7 8 9 10
x

21. Гиперболические функции

Гиперболический синус
y sh x
y
e x e x
y sh x
2
1
2
1
1
1
2
x
y ch x
y
Гиперболический косинус
e x e x
y ch x
2
1
2
1
1
1
2
x

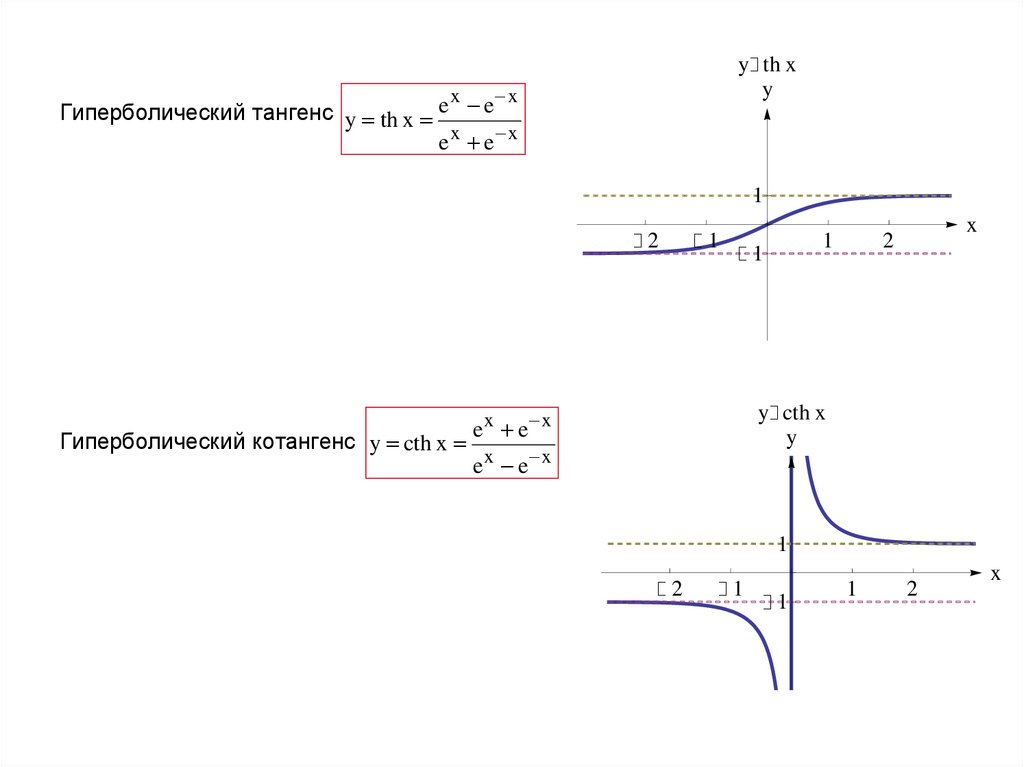
22.

y th x
y
x
x
Гиперболический тангенс y th x e e
e x e x
1
2
Гиперболический котангенс y cth x
1
1
1
x
2
y cth x
y
e x e x
e x e x
1
2
1
1
1
2
x

23.

Из определений следуют формулы:
ch 2 x sh 2 x 1;
ch ( x y) ch x ch y sh x sh y;
sh ( x y) sh x ch y ch x sh y;

24. Сравнение бесконечно малых.

Определения.
Пусть
Тогда:
( x) и ( x)
- бесконечно малые при
–
( x) , то говорят,
lim
0
x x ( x)
что бесконечно малая (x ) имеет более
–
высокий порядок малости, чем (x)
–
2. Если
–
1. Если
o
( x)
lim
x x ( x)
o
(x)
что бесконечно малая
–
более высокий порядок малости, чем
–
–
Обозначение:
( )
, то говорят,
–
–
x xo
имеет
(x) Обозначение: ( )
( x)
( x)
lim
k (k 0, )
3. Если
1 ,то
4. Если lim
x xo ( x)
x x ( x)
, то говорят, что бесконечно малые ( x) и ( x)
бесконечно малые ( x) и ( x)
o
имеют одинаковый порядок малости.
называются эквивалентными.
Обозначение:
(x) ~ ( x)

25. Сравнение бесконечно малых.

Пусть ( x) и ( x) бесконечно малые при x x0
Свойства эквивалентных бесконечно малых.
~ ~
2. ~ , ~ ~
– 1.
Доказательство свойства 1:
–
lim
– 3.
~ 1 , ~ 1
lim
x xo
– 4.
x xo
lim 1
x x 1
o
lim 1 1 1
lim
x x
x x
o
o
(если lim
x xo
1
)
1
Доказательство свойства 4:
~ ( ) ( )
Необходимость:
1.
2.
1
lim
1 lim
1 1 0
x xo
x xo
Д.з. Доказать достаточность.

26. Доказательство свойства 3: предел бесконечно малых не изменится, если их заменить на эквивалентные

так как
'
1
x x0
и
'
lim
1
x x0
lim

27. Свойство 5

• Если
есть бесконечно малая высшего порядка, чем
• , т.е. o( ) при x x o ,то ~ при x x o
Доказательство
lim lim 1
x x 0
x x 0
x x 0
lim
то есть
~ при x x o

28. Практический вывод

0
0
• При раскрытии неопределенности типа
бесконечно малые
сомножители можно заменять на эквивалентные.
• Бесконечно малые слагаемые можно отбрасывать.
• Пример.
lim
x 0
sin 2 x
2x
lim
2
x 2 x
x x3

29. Таблица эквивалентных бесконечно малых

• При
• 1.
• 2.
x 0
sin x ~ x
(следует из 1 замечательного
предела)
x
0
tg x ~ x
tg x
sin x
sin x
1
lim
lim
lim
1
x 0 x
x 0 x cos x
x 0
x x 0 cos x
lim
• 3.
arctg x ~ x
• Сделаем замену y arctg x, при x 0, y 0
arctg x
y
lim
1
x 0
y 0 tg y
x
lim
тогда

30. Продолжение таблицы эквивалентных бесконечно малых

• 4. arcsin x ~ x
• 5. ln (1 x) ~ x
• 6.
log a (1 x) ~
• так как
x
ln a
log a (1 x)
ln( 1 x )
ln a

31. Продолжение таблицы эквивалентных бесконечно малых

Аналогично докажем
7.
x
Замена
8. a x 1 ~ x ln a
9.
Частный случай
e 1 ~ x
y e x 1, при x 0, y 0 , тогда
(1 x )m 1 ~ mx
1 x 1 ~
x
2
ex 1
y
lim
lim
1
x 0
y 0 ln( 1 y)
x

32. Продолжение таблицы эквивалентных бесконечно малых

• 10.
x2
1 - cosx ~
2

33. Пример

ln( 1 2 x )
2x 1
lim
x 0 arctg 4 x
x 0 4x
2
lim

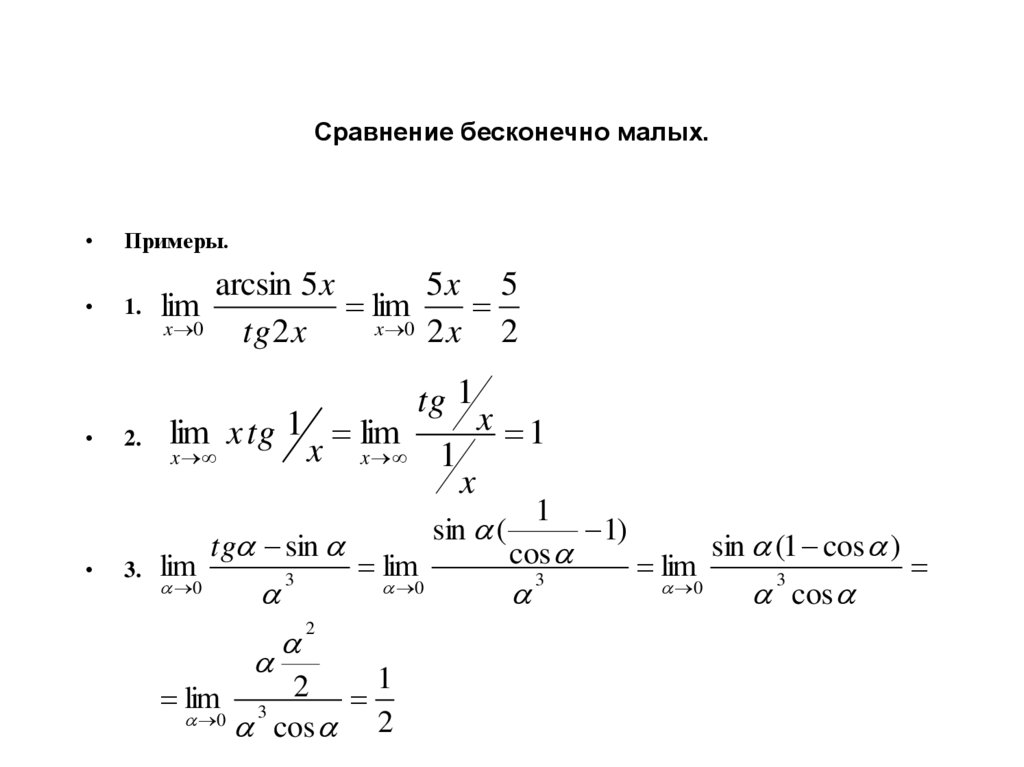
34. Сравнение бесконечно малых.

Примеры.
1.
arcsin 5 x
5x 5
lim
lim
x 0
x 0 2 x
tg 2 x
2
tg 1
2.
3.
x 1
lim x tg 1 lim
x x 1
x
x
lim
0
tg sin
3
lim
0
2
1
2
lim 3
0
cos 2
sin (
1
1)
sin (1 cos )
cos
lim
3
3
0
cos

35.

36.

37.

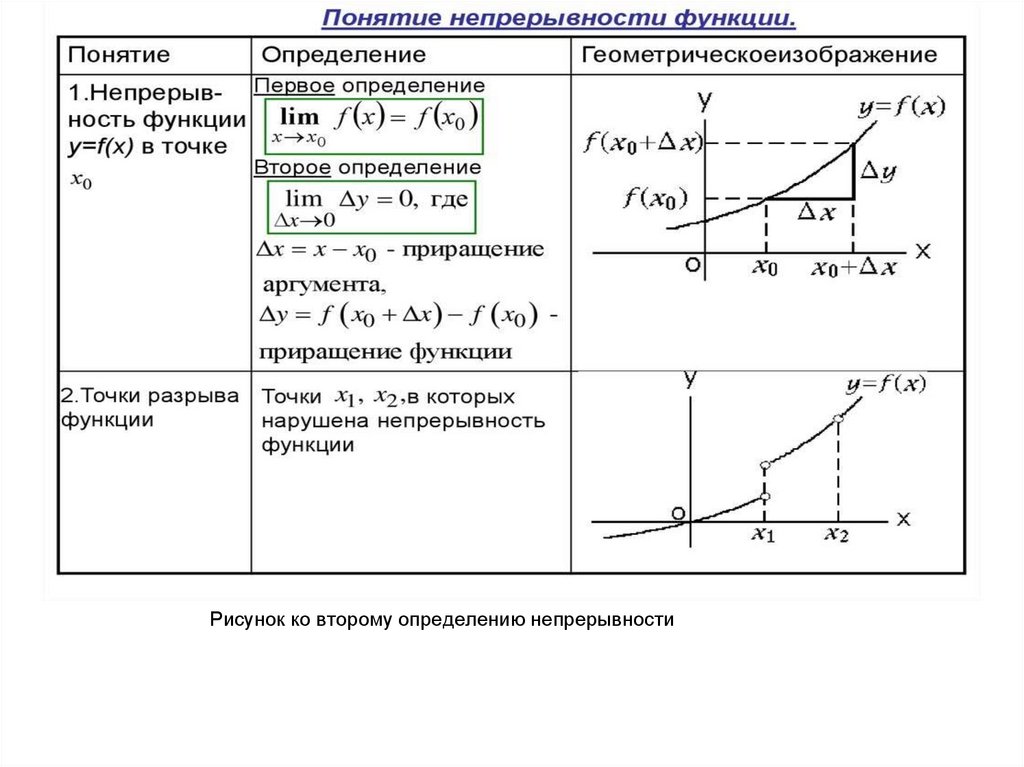
38. Определение 1 на языке

• Y=f(x) называется непрерывной в точке x 0 ,
если она определена в этой точке и
некоторой ее окрестности и 0 ( )
такое, что x : | x - x 0 | | f (x) f (x 0 |

39.

• Наличие lim f (x) связано с равенством
левого и правого пределов функции в
точке x 0 , то есть
x x 0
lim f (x) lim f (x) f (x 0 )
x x 0 0
x x 0 0

40. Из определения следует, что в точке непрерывности можно менять местами символы функции и предела, т.е.

lim f (x) f ( lim x)
x x 0
x x 0
Действительно,
lim f (x) f (x 0 ) f ( lim x)
x x 0
x x 0
Пример.
lim sin x sin( lim x ) sin
x
4
x
4
2
4
2

41.

Определение 2
(следующий слайд)

42.

43.

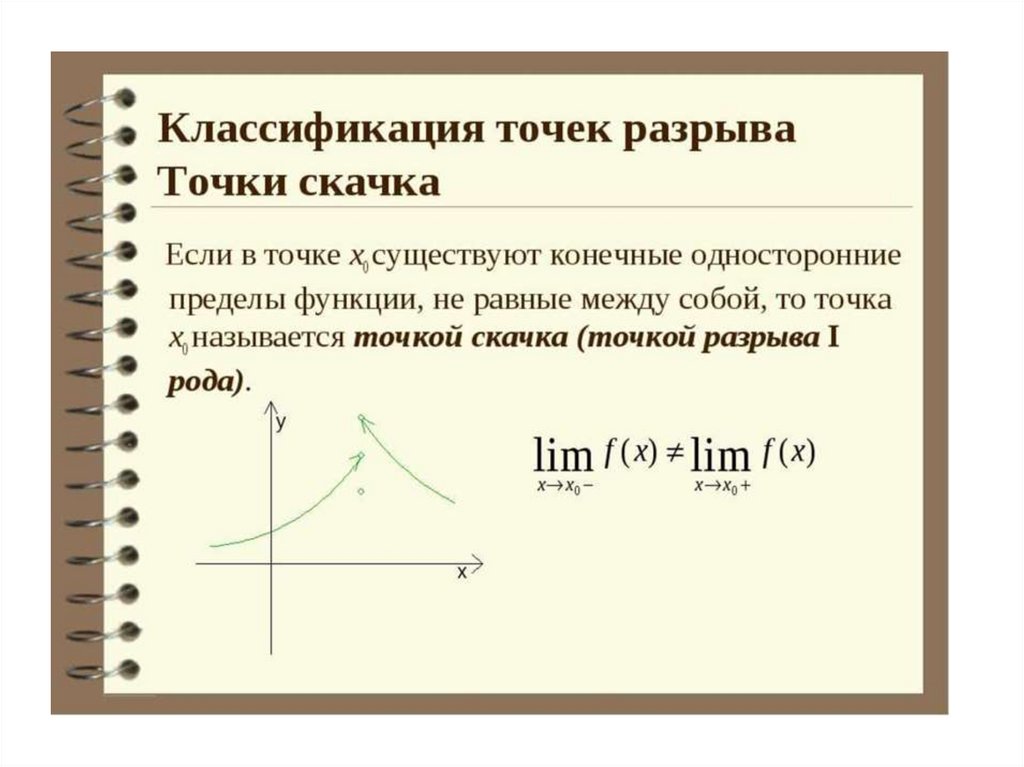
Рисунок ко второму определению непрерывности

44.

45.

46. Оба определения непрерывности функции в точке эквивалентны.

Доказательство. Из 1 2
Пусть lim f (x) f (x 0 ) , тогда по теореме о разности между
x x
функцией и ее пределом будет:
f (x) f (x 0 ) ( x) , где ( x ) - бесконечно малая при
0
x x 0 , т.е. x 0
Но (x) f (x) f (x 0 ) y, т.е. y - является бесконечно
малой при x 0 .

47. Непрерывность основных элементарных функций в точках области определения

Основные элементарные функции непрерывны в каждой
точке, в которой они определены.
y sin x
Доказательство для
lim y lim [sin( x x ) sin x ] lim 2 sin
x 0
x 0
x 0
lim x cos(x
x 0
Использовано: sin
x
x
x
x
cos( x ) lim 2 cos( x )
x 0
2
2
2
2
x
) 0
2
x x
~
при x 0
2
2

48. Теоремы о непрерывности суммы, разности, произведения и частного двух непрерывных функций

f ( x ) и ( x )
x0
( x 0 ) 0
f ( x ) ( x )
f (x)
( x )
x0

49. Доказательство для произведения.

Пусть
y f ( x ) ( x )
lim [f (x) (x)] lim f (x) lim (x) f (x 0 ) (x 0 )
x x 0
x x 0
x x 0

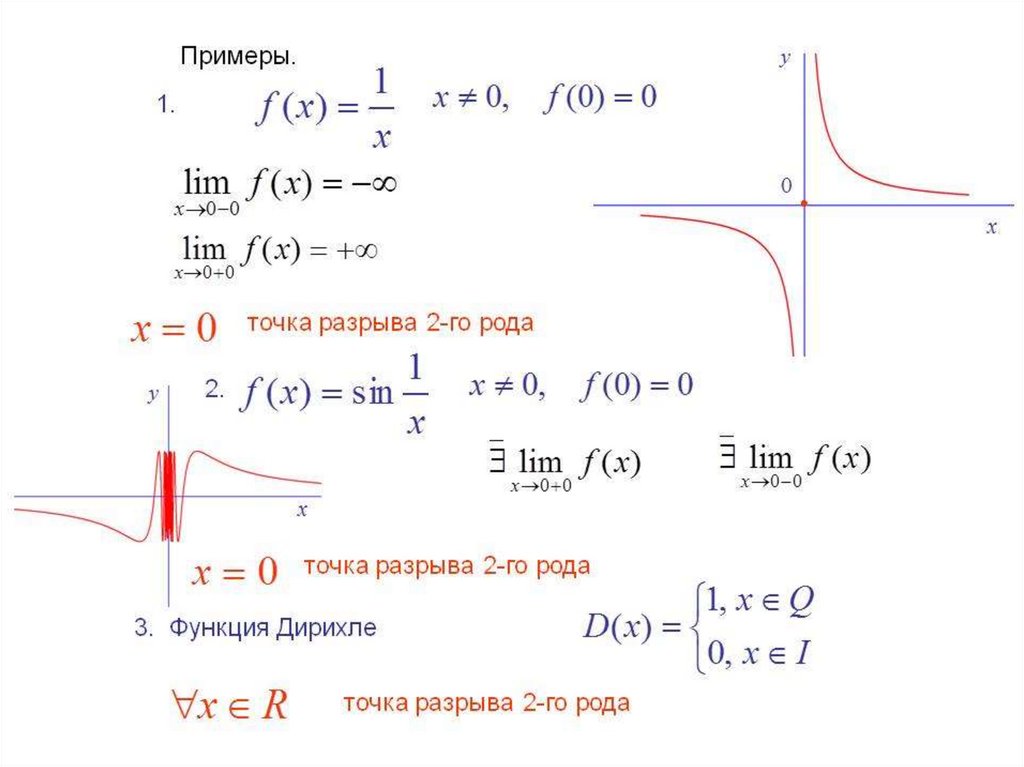
50.

51.

52.

53.

54.

55.

56.

57.

58. Пример

| x|
y
x

59. Пример

| x|
y
x
x = 0 - точка разрыва
| x|
x
lim
lim
1
x 0 x
x 0 x
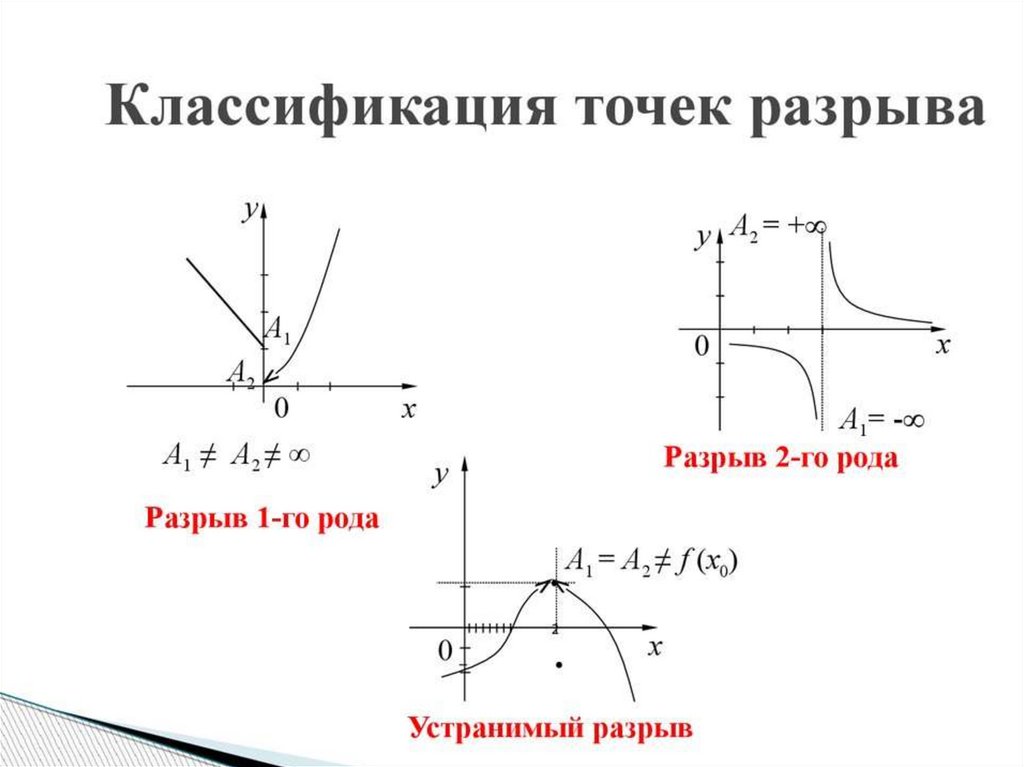
• X=0 - точка разрыва I рода (скачок)

60.

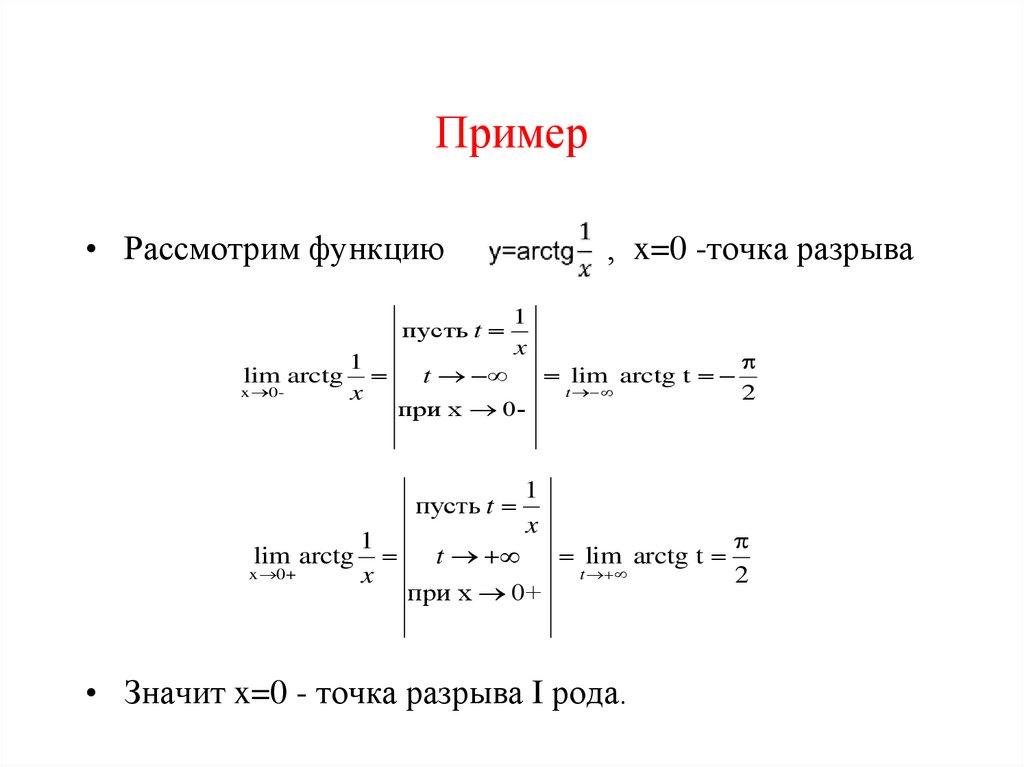
61. Пример

• Рассмотрим функцию
пусть t
lim arctg
x 0-
1
x
, x=0 -точка разрыва
1
x
t
при x 0-
пусть t
lim arctg
x 0+
lim arctg t
1
x
t
1
x
t
при x 0+
lim arctg t
t
• Значит x=0 - точка разрыва I рода.
2
2

62.

63.

64.

65.

66.

67.

68.

69.

70.

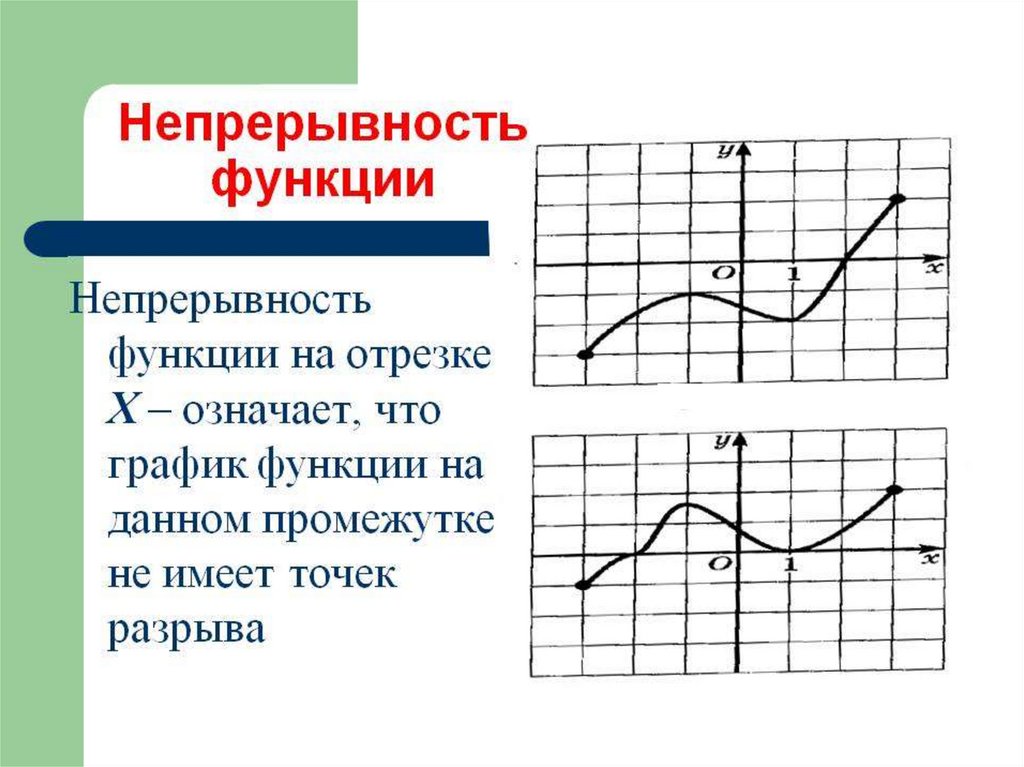
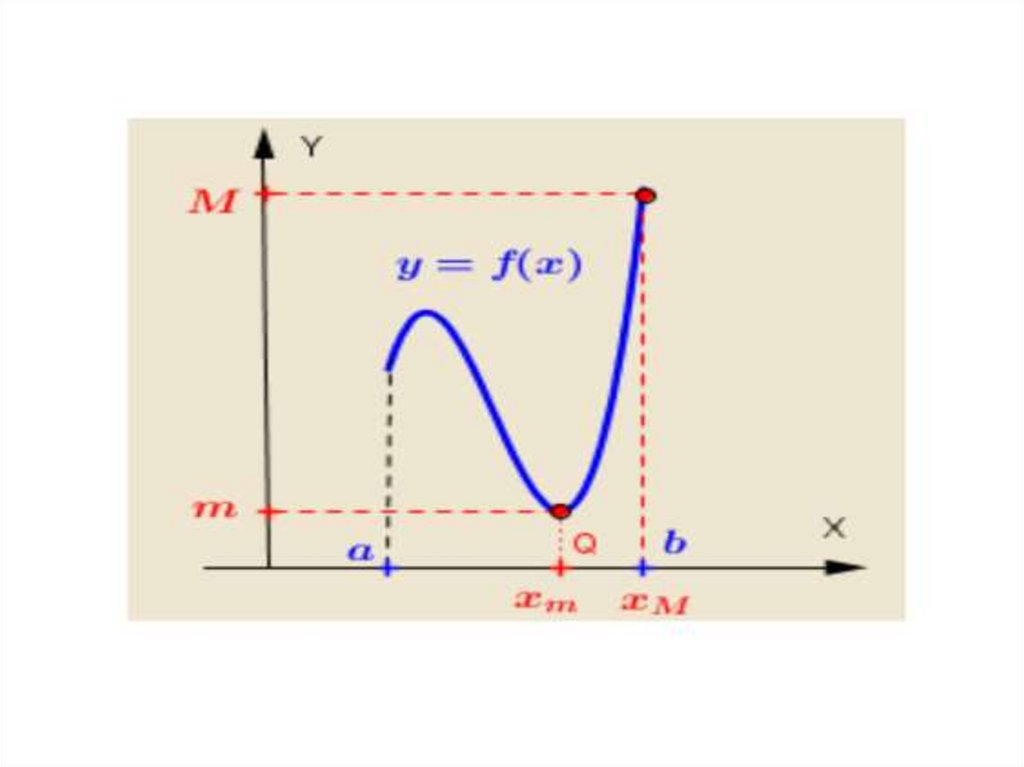
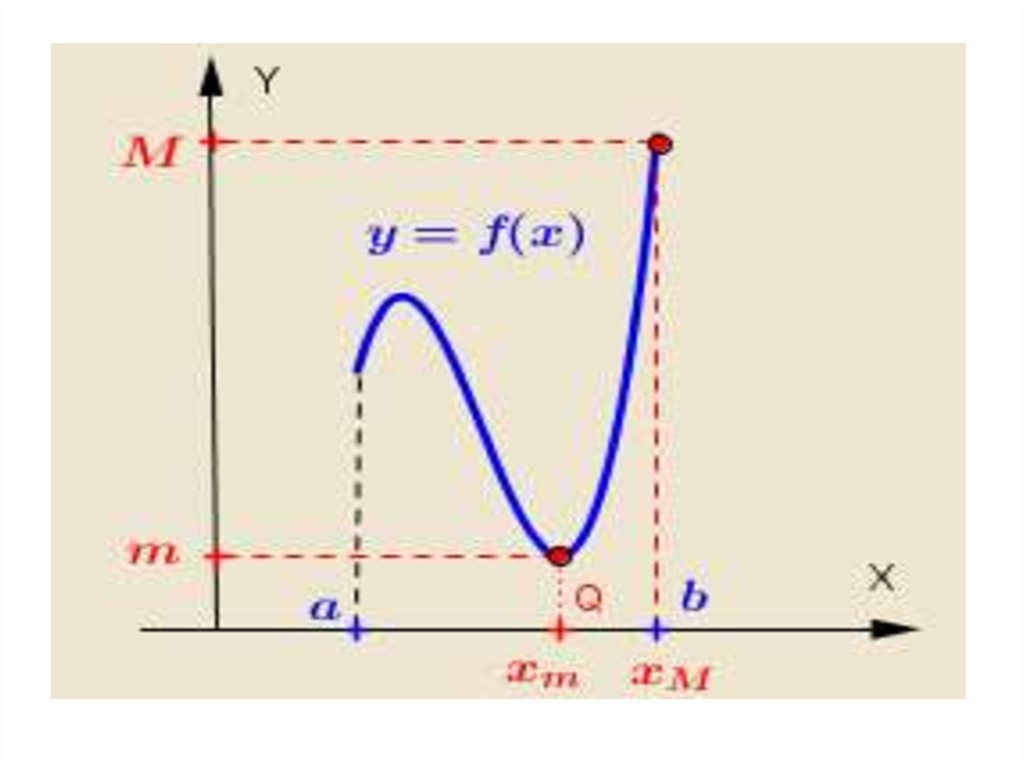
• Если функция непрерывна на замкнутом
интервале, то она достигает на нем
своего наибольшего и наименьшего
значений.
f ( xm ) yнаим. ; f ( xM ) yнаиб.

71.

72.

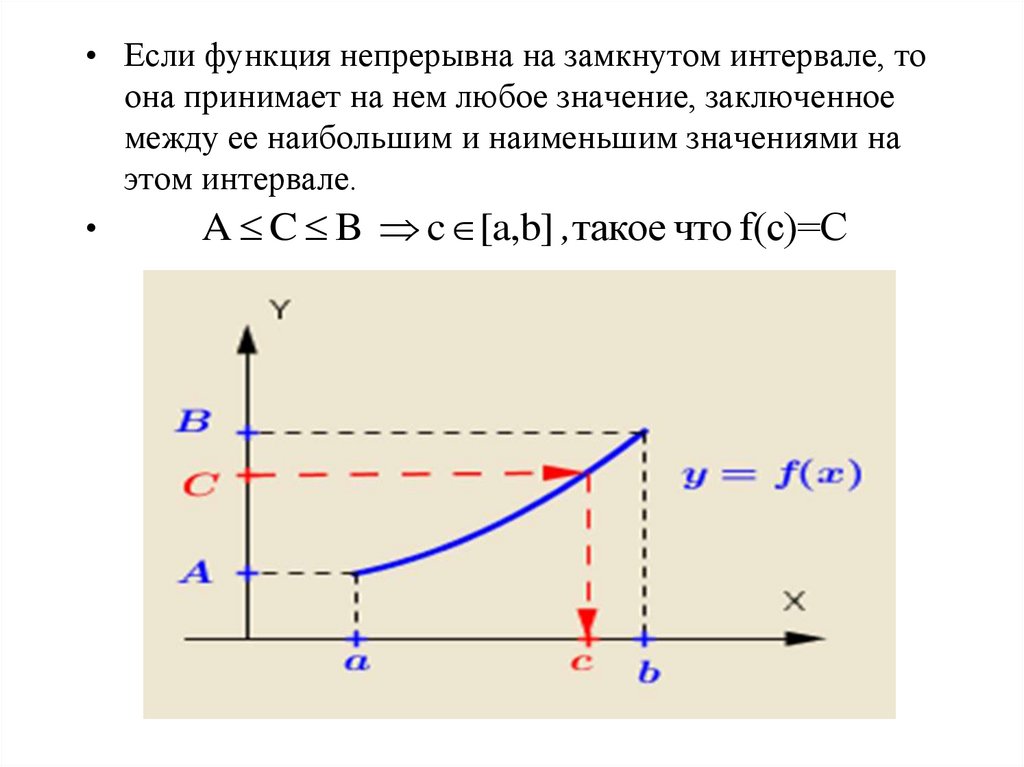
• Если функция непрерывна на замкнутом интервале, то
она принимает на нем любое значение, заключенное
между ее наибольшим и наименьшим значениями на
этом интервале.
A C B c [a,b] ,такое что f(c)=C