Занятие 2.1

1.

Логика

2.

Определение
• Математическая логика — это наука о
законах и формах правильного мышления,
выраженных в формальном виде.
• Логическое высказывание — это
повествовательное предложение, о
котором можно однозначно сказать,
истинно оно или ложно.

3.

Примеры
• "Москва — столица России" (истина, 1,
TRUE)
• "2 + 2 = 5" (ложь, 0, FALSE)
• "Который час?" (не высказывание)
• "Закройте дверь!" (не высказывание)

4.

Таблица истинности
• — это таблица, которая показывает
результат выполнения логической
операции или логического выражения для
всех возможных комбинаций входных
значений.

5.

Логические операции
• Отрицание (Инверсия, НЕ, NOT)
• Обозначения: ¬A, NOT A, Ā, !A
• | A | ¬A |
• |0|1 |
• |1|0 |

6.

Логические операции
• Конъюнкция (Логическое умножение, И,
AND)
• Обозначения: A ∧ B, A AND B, A · B, A & B
• Истинна только когда ОБА операнда
истинны
• |A|B|A∧B|
• |0|0|0 |
• |0|1|0 |
• |1|0|0 |
• |1|1|1 |

7.

Логические операции
• Дизъюнкция (Логическое сложение, ИЛИ,
OR)
• Обозначения: A ∨ B, A OR B, A + B, A | B
• Истинна, когда ХОТЯ БЫ ОДИН операнд
истинен
• |A|B|A∧B|
• |0|0|0 |
• |0|1|1 |
• |1|0|1 |
• |1|1|1 |

8.

Логические операции
• Исключающее ИЛИ (XOR)
• Обозначения: A ⊕ B, A XOR B
• Истинна, когда операнды РАЗЛИЧНЫ
• |A|B|A∧B|
• |0|0|0 |
• |0|1|1 |
• |1|0|1 |
• |1|1|0 |

9.

Логические операции
• Импликация (Следование, ЕСЛИ-ТО)
• Обозначения: A → B, A ⇒ B
• Ложна только когда из ИСТИНЫ следует
ЛОЖЬ
• |A|B|A∧B|
• |0|0|1 |
• |0|1|1 |
• |1|0|0 |
• |1|1|1 |

10.

Логические операции
• Эквиваленция (Равносильность)
• Обозначения: A ≡ B, A ↔ B, A ~ B
• Истинна, когда операнды ОДИНАКОВЫ
• |A|B|A∧B|
• |0|0|1 |
• |0|1|0 |
• |1|0|0 |
• |1|1|1 |

11.

Логические операции в Python
• ∧ - and
• ∨ - or
• ¬ - not
• → - (not A) or B
• → - A <= B
• ↔ - A == B

12.

Порядок логических операций
• Порядок выполнения (от высшего к
низшему):
• 1. NOT (¬)
• 2. AND (&, ∧)
• 3. OR (|, ∨)
• 4. XOR (⊕)
• 5. → (импликация)
• 6. ↔ (эквивалентность)
• Скобки имеют наивысший приоритет.

13.

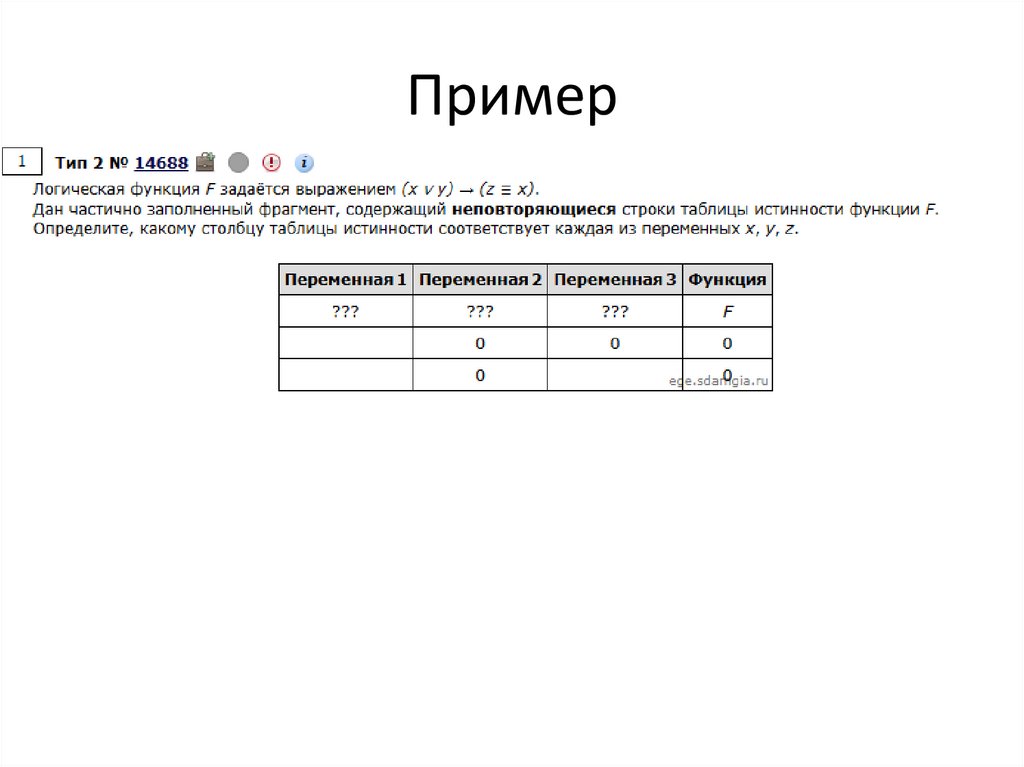
Задание ЕГЭ №2
• Дана логическая функция F и неполная
таблица истинности с несколькими
строками. Нужно определить, какому
столбцу (переменной) соответствует
каждая из переменных x, y, z.

14.

Пример

15.

Решение

16.

Задача 1

17.

Задача 2

18.

Задача 3

19.

Задача 4

20.

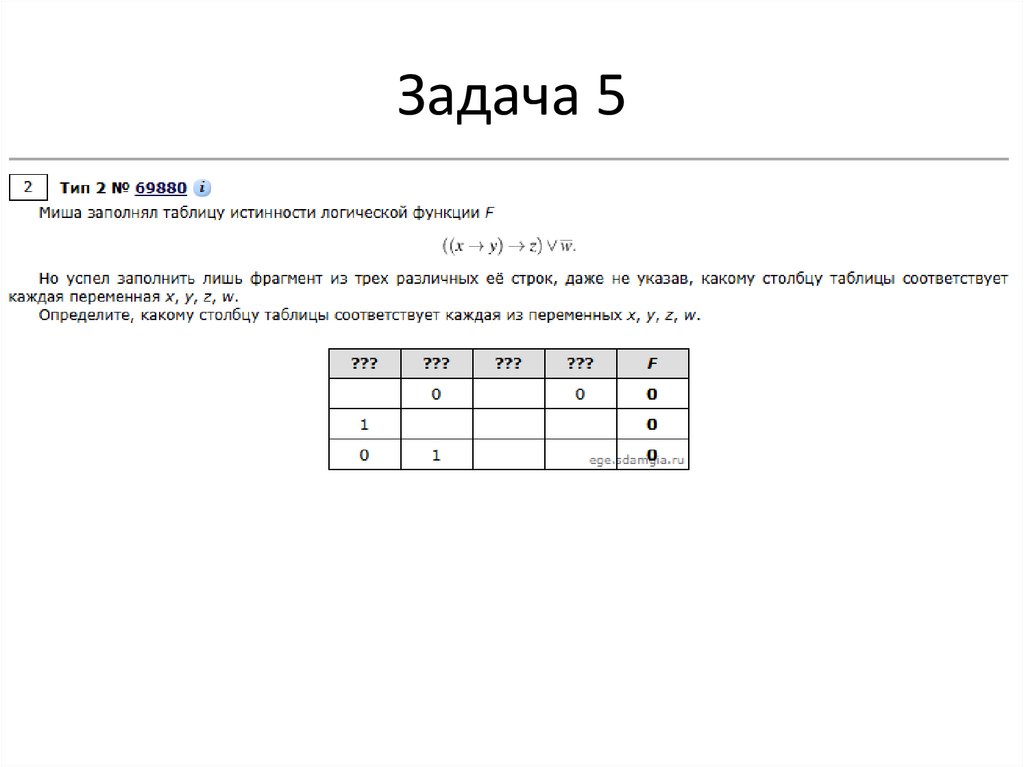
Задача 5

21.

Ответы
• 1) zyxw
• 2) ywzx
• 3) wxzy
• 4) zxyw
• 5) xywz

22.

Задание ЕГЭ №15
• Преобразование логических выражений с
числовыми отрезками и координатной
плоскостью.
• Задания требуют найти параметры
отрезков или областей на плоскости, при
которых выражение становится
тождественно истинным для всех значений
переменных.

23.

Задача 6
• Обозначим через ДЕЛ(n, m) утверждение
«натуральное число n делится без остатка
на натуральное число m». Для какого
наибольшего натурального числа А
логическое выражение
• ¬ДЕЛ(x, А) → (ДЕЛ(x, 14) → ¬ДЕЛ(x, 4))
• истинно (т. е. принимает значение 1) при
любом целом положительном значении
переменной х?

24.

Решение 6
• def d(n, m):
return n%m==0
• def f(a,x):
return (not d(x,a)) <= (d(x,14) <= (not d(x,4)))
• for a in range(1000,1,-1):
if all(f(a,x) for x in range(1000000)):
print(a)
break

25.

Задача 7
• Обозначим через ДЕЛ(n, m) утверждение
«натуральное число n делится без остатка
на натуральное число m».Для какого
наименьшего натурального числа А
формула
• (ДЕЛ(x, 2) → ¬ДЕЛ(x, 5)) ∨ (x + A ≥ 70)
• тождественно истинна (т. е. принимает
значение 1) при любом целом

26.

Задача 8
• Для какого наименьшего целого
неотрицательного числа А логическое
выражение
• (x≥12)∨(3x<y)∨(xy<A)
• тождественно истинно (то есть принимает
значение 1) при любых целых
неотрицательных x и y?

27.

Задача 9
• Для какого наибольшего натурального
значения А выражение
• (y + 3x > A)∨(x < 20)∨(y < 50)
• тождественно истинно для любых
положительных и целых x и y. В ответ
запишите целое число — значение A?

28.

Побитовая конъюнкция
• 14 & 5 = 11102 & 01012 = 01002 = 4

29.

Задача 10
• Обозначим через m & n поразрядную
конъюнкцию неотрицательных целых чисел m и
n.
• Так, например, 14 & 5 = 11102 &
01012 = 01002 = 4. Для какого наименьшего
неотрицательного целого числа А формула
• x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)
• тождественно истинна (т. е. принимает значение
1 при любом неотрицательном целом значении
переменной x)?

30.

Задача 11
• Обозначим через m&n поразрядную
конъюнкцию неотрицательных целых чисел
m и n. Так, например,
14&5 = 11102&01012 = 01002 = 4.
• Для какого наименьшего неотрицательного
целого числа А формула
• тождественно истинна (т. е. принимает
значение 1 при любом неотрицательном
целом значении переменной x)?

31.

Отрезки
• Упрощение импликации — нужно найти
максимальную длину отрезка A, при
которой формула истинна для всех x.

32.

Задача 12
• На числовой прямой даны два отрезка:
P = [5, 30] и Q = [14, 23]. Укажите
наибольшую возможную длину
промежутка A, для которого формула
• ((x ∈ P) ≡ (x ∈ Q)) → ¬(x ∈ A)
• тождественно истинна, то есть принимает
значение 1 при любом значении
переменной х.

33.

Задача 13
• На числовой прямой даны два отрезка:
P = [25; 40] и Q = [11; 32]. Укажите
наименьшую возможную длину такого
отрезка A, для которого логическое
выражение
• (x ∈ P) → (((x ∈ Q) ∧ (x ∈ P)) → (x ∈ A))
• истинно (т. е. принимает значение 1) при
любом значении переменной х.

34.

Решение 13
• def f(x,a1,a2):
P = 25<=x<=40
Q = 11<=x<=32
A = a1<=x<=a2
return P <= ((Q and P) <= A)
• v = [dx for x in (25,40,11,32) for dx in (x,x+0.1,x-0.1)]
• m = []
• for a1 in v:
for a2 in v:
if a2>a1 and all(f(x,a1,a2) for x in v):
m.append(a2-a1)
• print(min(m))

35.

Ответы
• 6) 28
• 7) 60
• 8) 364
• 9) 109
• 10) 12
• 11) 44
• 12) 9
• 13) 7