Лекция 2_Проецирование прямой

1. Лекция 2 Тема: Проецирование прямой

ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ГРАФИКИ
Лекция 2
Тема: Проецирование прямой
РАЗРАБОТАЛИ: ст. преп. кафедры Н Г и Г – Крамаровская В.И.
ст. преп. кафедры Н Г и Г – Стаселько О.Л.
ст. преп. кафедры Н Г и Г – Шушарина И.В.

2. Проецирование прямой

3.

• Прямая – это траектория движущейся в пространстве точки
от одной к другой, по кратчайшему расстоянию
Прямая может быть задана:
- координатами двух точек (отрезок);
- координатами одной точки и углом наклона к плоскости;
- координатами одной точки и направлением (вектор)

4.

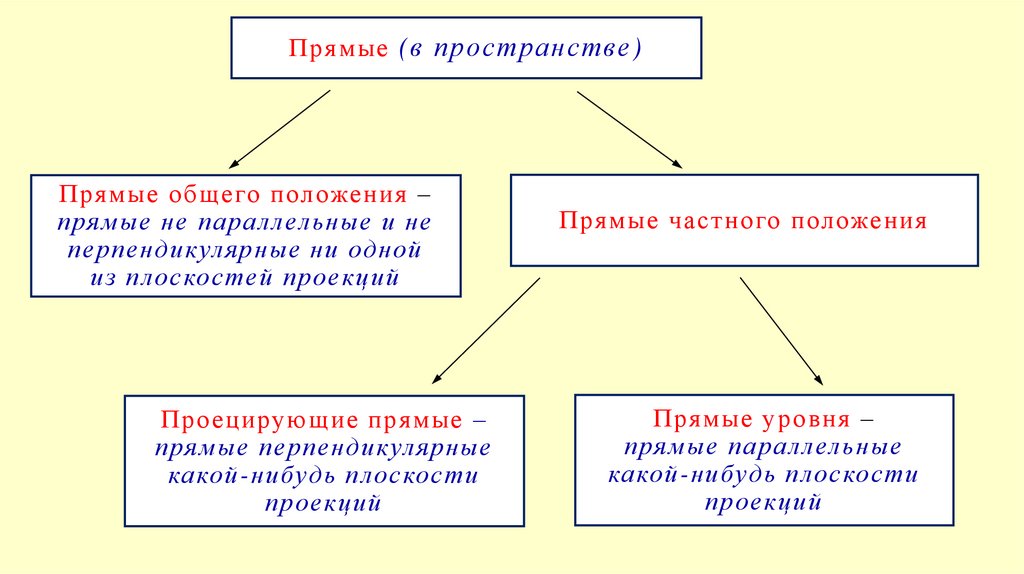
Прямые (в пространстве)
Прямые общего положения –
прямые не паралл ельные и не
перпендикулярные ни одной
из плоскостей проекций
Проецирующие прямые –
прямые перпендикулярные
какой-нибудь плоскости
проекций
Прямые частного положения
Прямые уровня –
прямые паралл ельные
какой-нибудь плоскости
проекций

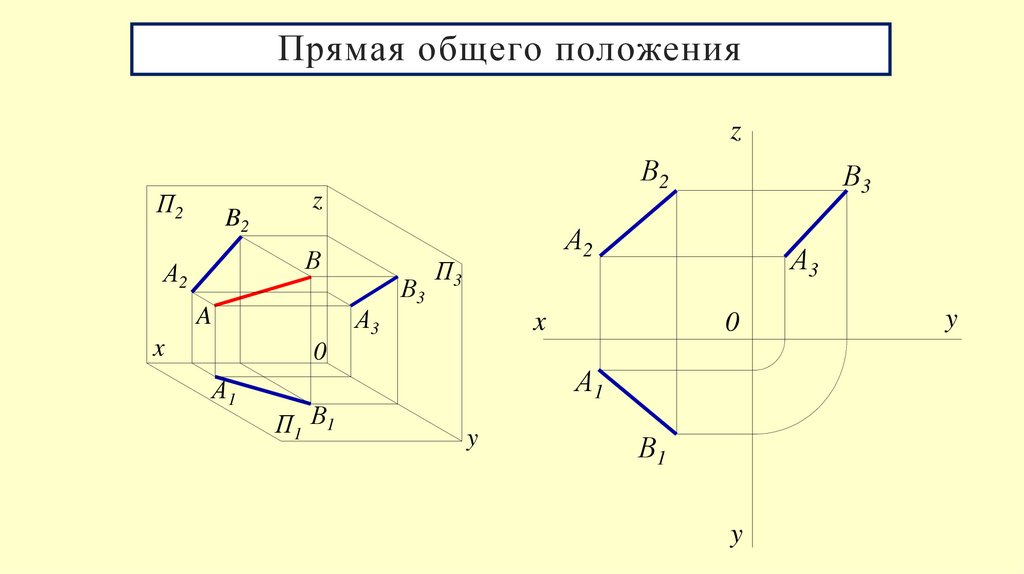
5. Прямая общего положения

z
П2
B2
В2
z
В
А2
А3
A
x
В3
А2
П3
П1 В1
А3
x
0
А1
В3
0
А1
y
В1
y
y

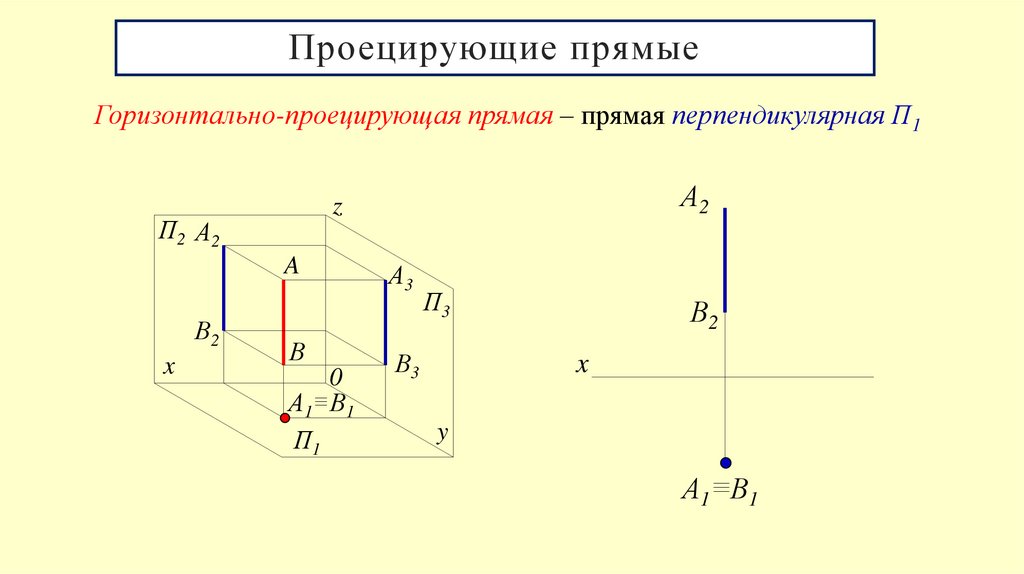
6. Проецирующие прямые

Горизонтально-проецирующая прямая – прямая перпендикулярная П1
П2 А2
A
В2
x
А2
z
В
0
А1≡В1
П1
А3
П3
В3
В2
x
y
А1≡В1

7.

Фронтально-проецирующая прямая – прямая перпендикулярная П2
А2≡В2
x
А1
В1

8.

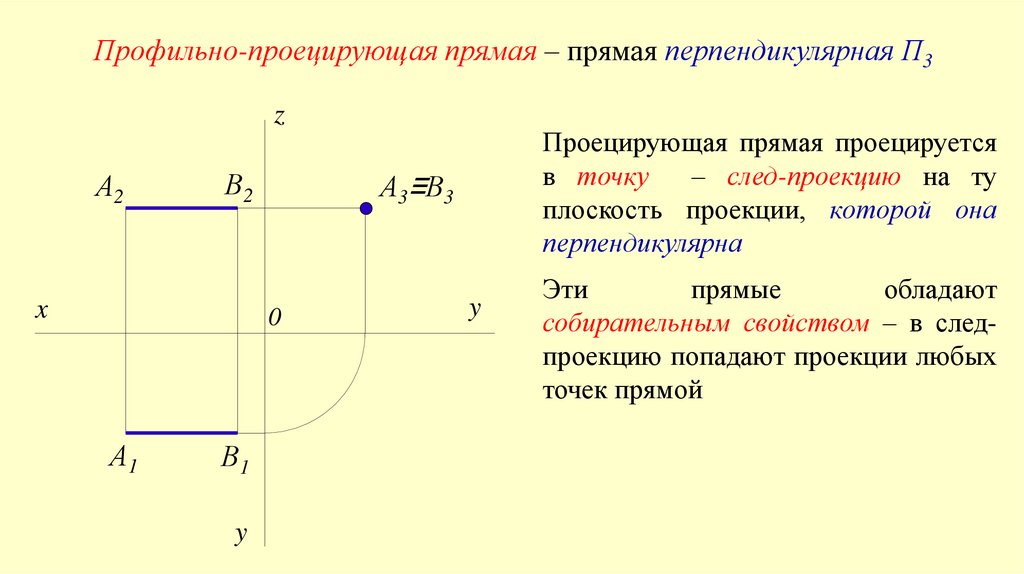
Профильно-проецирующая прямая – прямая перпендикулярная П3
z
А2
А3≡В3
В2
x
0
А1
В1
y
Проецирующая прямая проецируется
в точку
– след-проекцию на ту
плоскость проекции, которой она
перпендикулярна
y
Эти
прямые
обладают
собирательным свойством – в следпроекцию попадают проекции любых
точек прямой

9. Прямые уровня

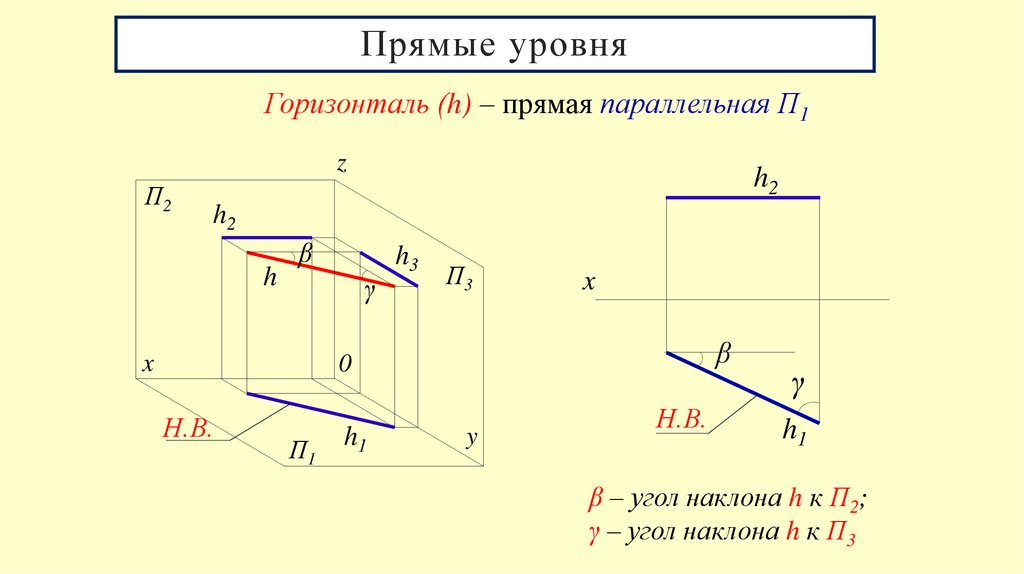
Горизонталь (h) – прямая параллельная П1
z
П2
h2
h2
h
β
γ
x
h3
П3
x
β
0
Н.В.
П1
h1
y
Н.В.
γ
h1
β – угол наклона h к П2;
γ – угол наклона h к П3

10.

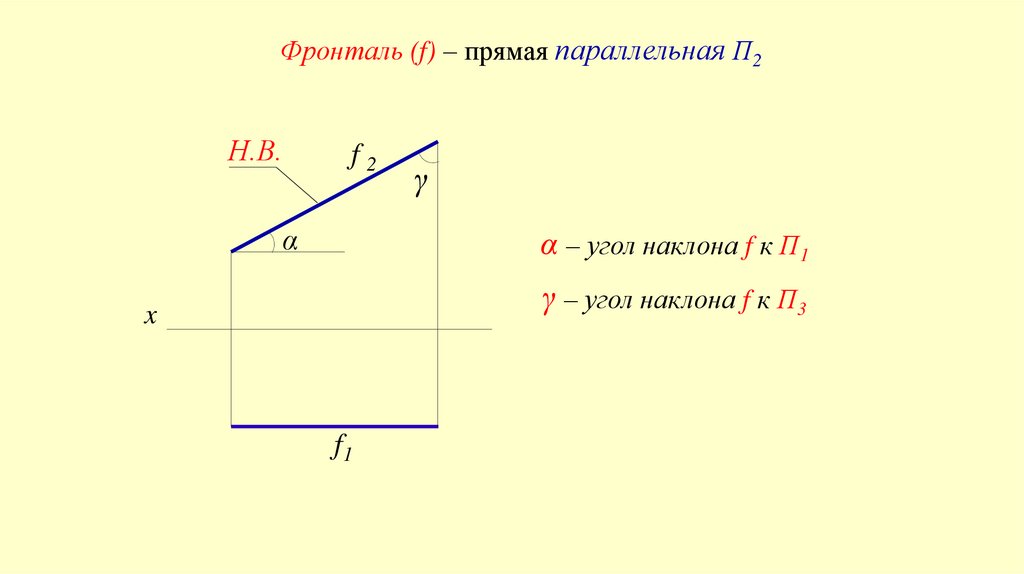
Фронталь (f) – прямая параллельная П2
Н.В.
f2
α
γ
α – угол наклона f к П1
γ – угол наклона f к П3
x
f1

11.

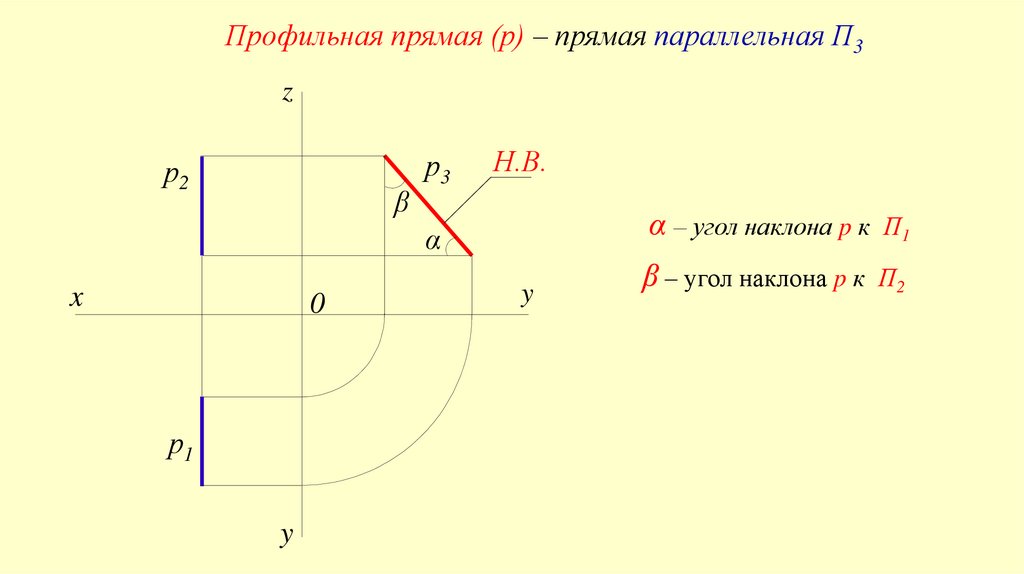
Профильная прямая (р) – прямая параллельная П3
z
р2
β
р3
Н.В.
α – угол наклона p к П1
α
x
0
р1
y
y
β – угол наклона p к П2

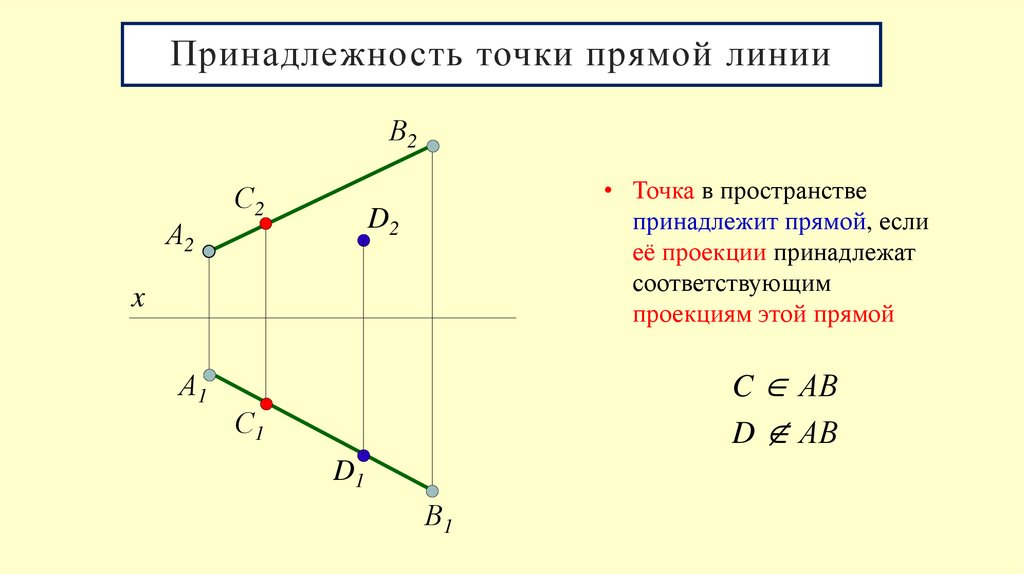
12. Принадлежность точки прямой линии

В2
А2
С2
• Точка в пространстве
принадлежит прямой, если
её проекции принадлежат
соответствующим
проекциям этой прямой
D2
x
А1
C АВ
D АВ
С1
D1
В1

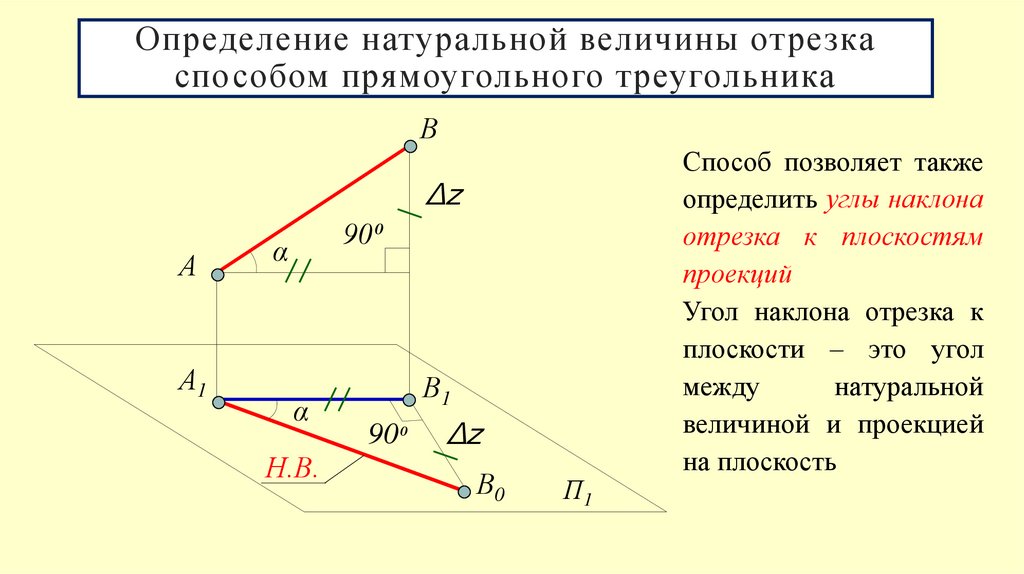
13. Определение натуральной величины отрезка способом прямоугольного треугольника

В
∆z
А
А1
90⁰
α
α
Н.В.
В1
90⁰
∆z
В0
П1
Способ позволяет также
определить углы наклона
отрезка к плоскостям
проекций
Угол наклона отрезка к
плоскости – это угол
между
натуральной
величиной и проекцией
на плоскость

14.

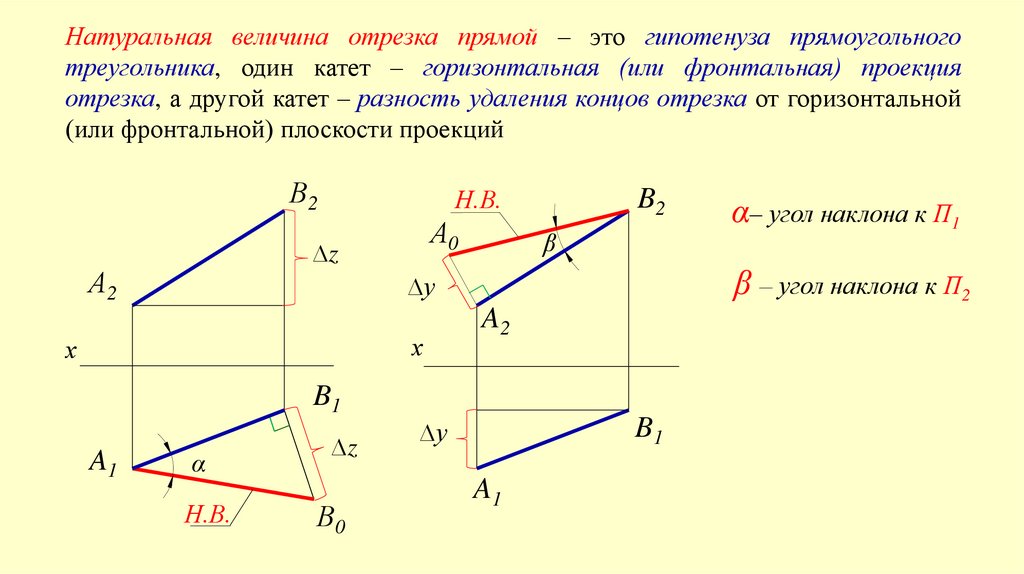
Натуральная величина отрезка прямой – это гипотенуза прямоугольного
треугольника, один катет – горизонтальная (или фронтальная) проекция
отрезка, а другой катет – разность удаления концов отрезка от горизонтальной
(или фронтальной) плоскости проекций
В2
Н.В.
А0
∆z
А2
β
х
A2
B1
α
Н.В.
∆z
В0
α– угол наклона к П1
β – угол наклона к П2
∆у
х
A1
B2
B1
∆у
A1

15.

Взаимное положение прямых в пространстве
скрещивающиеся
параллельные
пересекающиеся

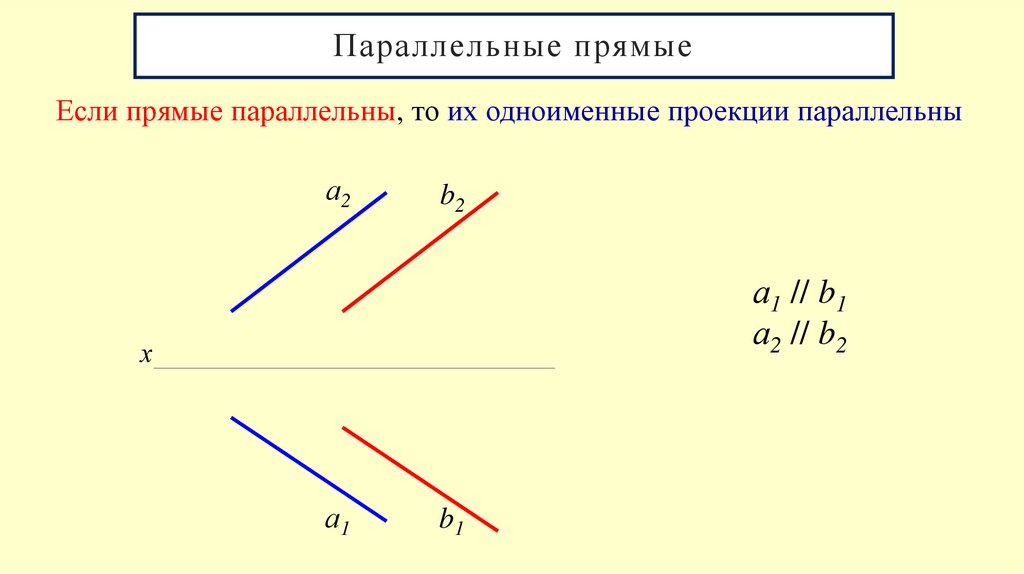
16. Параллельные прямые

Если прямые параллельны, то их одноименные проекции параллельны
а2
b2
а1 // b1
а2 // b2
х
а1
b1

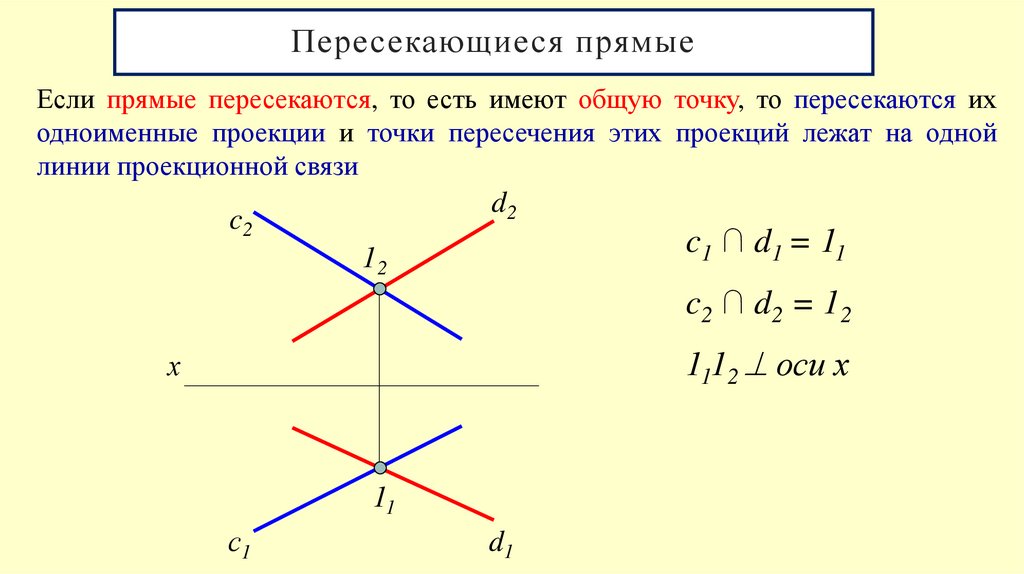
17. Пересекающиеся прямые

Если прямые пересекаются, то есть имеют общую точку, то пересекаются их
одноименные проекции и точки пересечения этих проекций лежат на одной
линии проекционной связи
d2
c2
12
c1 ∩ d1 = 11
c2 ∩ d2 = 12
1112 оси х
х
11
с1
d1

18. Скрещивающиеся прямые

Скрещивающиеся прямые в пространстве лежат в разных плоскостях и общих
точек не имеют
m2
n2
12≡ 22
32
42
х
11
21
n1
31≡ 41
m1
• Точки
кажущегося
пересечения
скрещивающихся прямых называются
конкурирующими
• Из двух конкурирующих точек
видимой будет та, противоположная
проекция которой, находится дальше
от оси х
• Точки 2 и 3 видимые, так как
находятся дальше от оси х или ближе
к наблюдателю

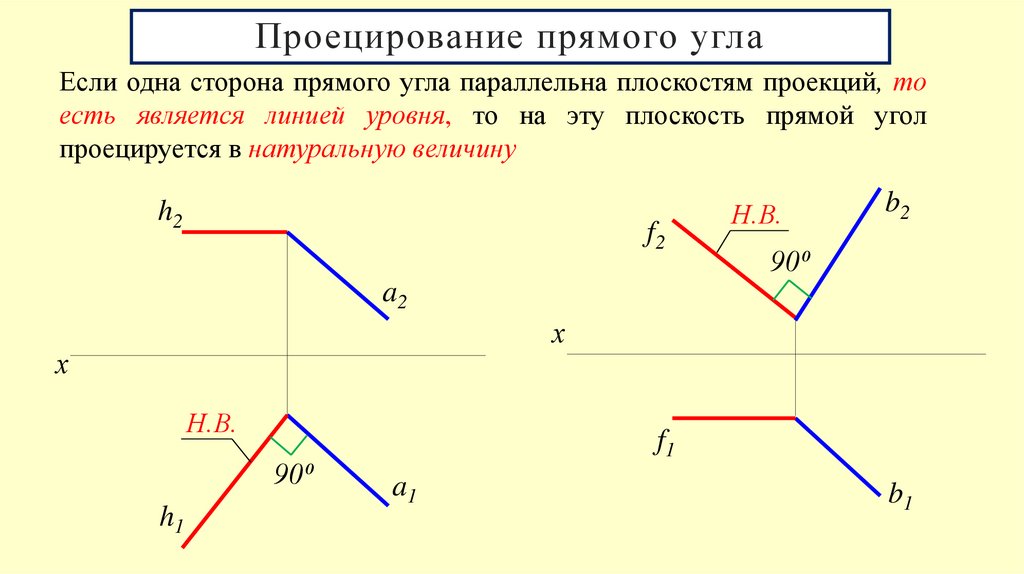
19. Проецирование прямого угла

Если одна сторона прямого угла параллельна плоскостям проекций, то
есть является линией уровня, то на эту плоскость прямой угол
проецируется в натуральную величину
h2
f2
Н.В.
b2
90⁰
a2
х
х
Н.В.
90⁰
h1
f1
a1
b1

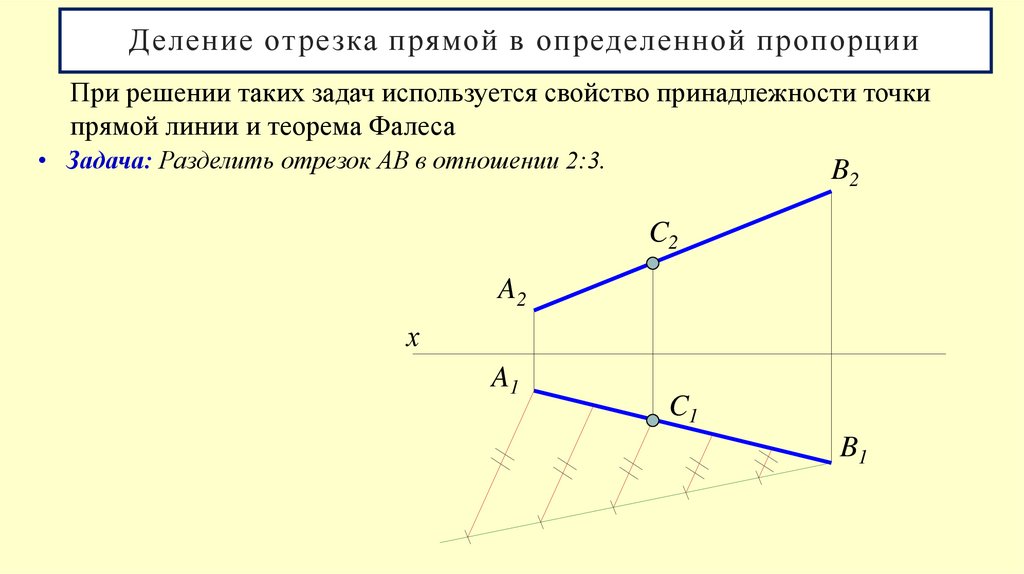
20. Деление отрезка прямой в определенной пропорции

При решении таких задач используется свойство принадлежности точки
прямой линии и теорема Фалеса
• Задача: Разделить отрезок АВ в отношении 2:3.
B2
C2
A2
х
A1
C1
B1