Преобразование тригонометрических функций_

1. Преобразования графиков тригонометрических функций

2. Задачи урока

Повторить правила
преобразований функций:
y f (x t)
y f ( x) m
y f (kx)
y af ( x)

3. Задачи урока

Построить графики
тригонометрических функций с
помощью преобразований

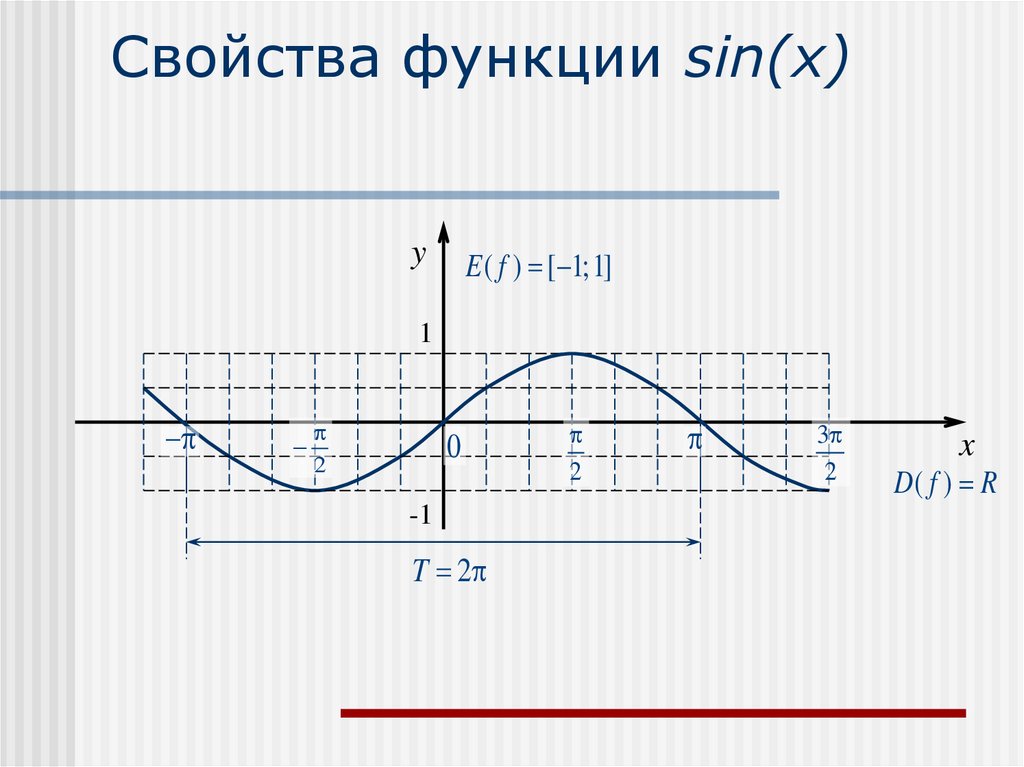
4. Свойства функции sin(x)

y
E ( f ) [ 1;1]
1
2
0
-1
T 2
2
3
2
x
D( f ) R

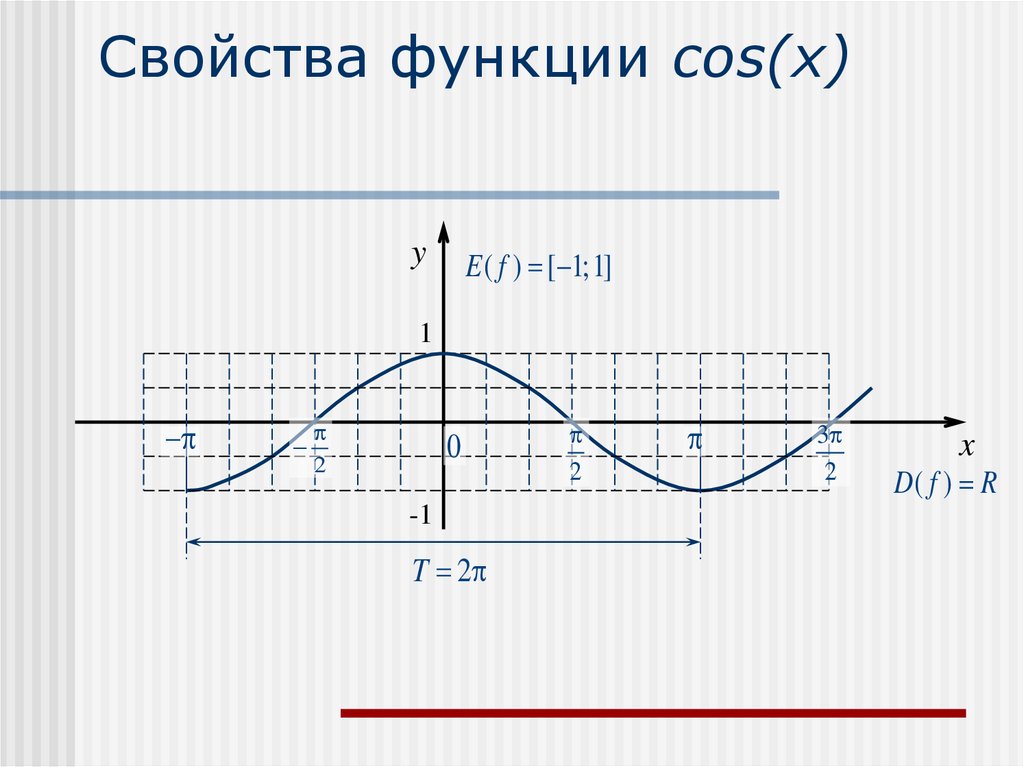
5. Свойства функции cos(x)

y
E ( f ) [ 1;1]
1
2
0
-1
T 2
2
3
2
x
D( f ) R

6.

Преобразование графиков
тригонометрических функций
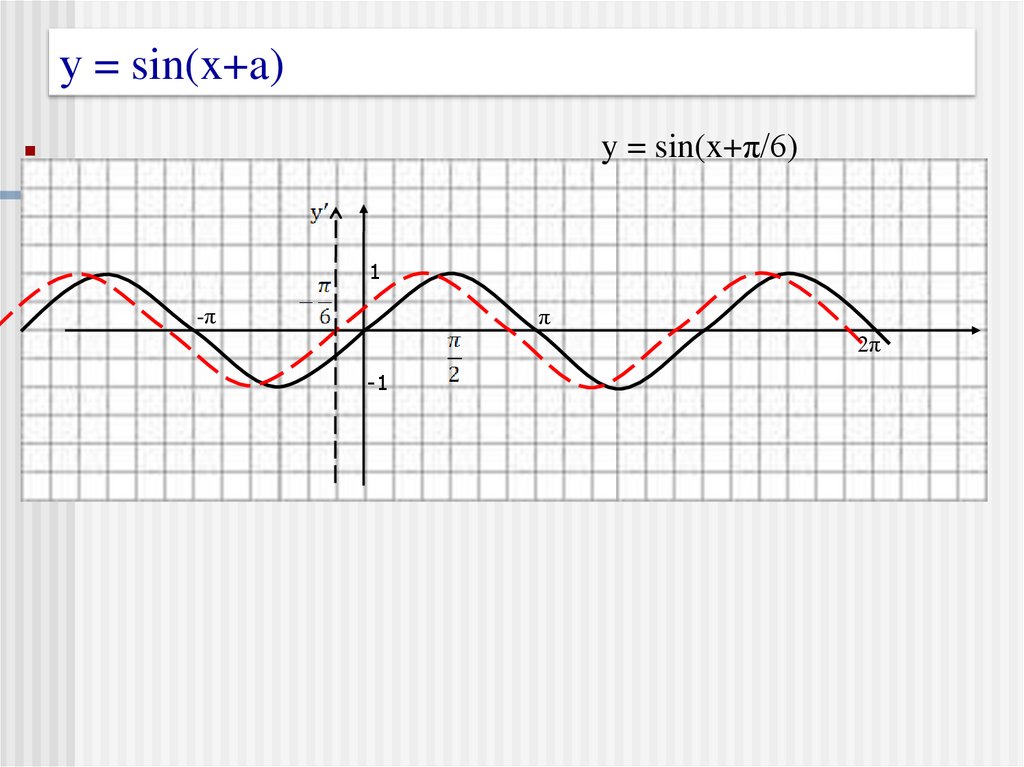
График функции у = f (x+b) получается из
графика функции у = f(x) параллельным
переносом на (-b) единиц вдоль оси абсцисс
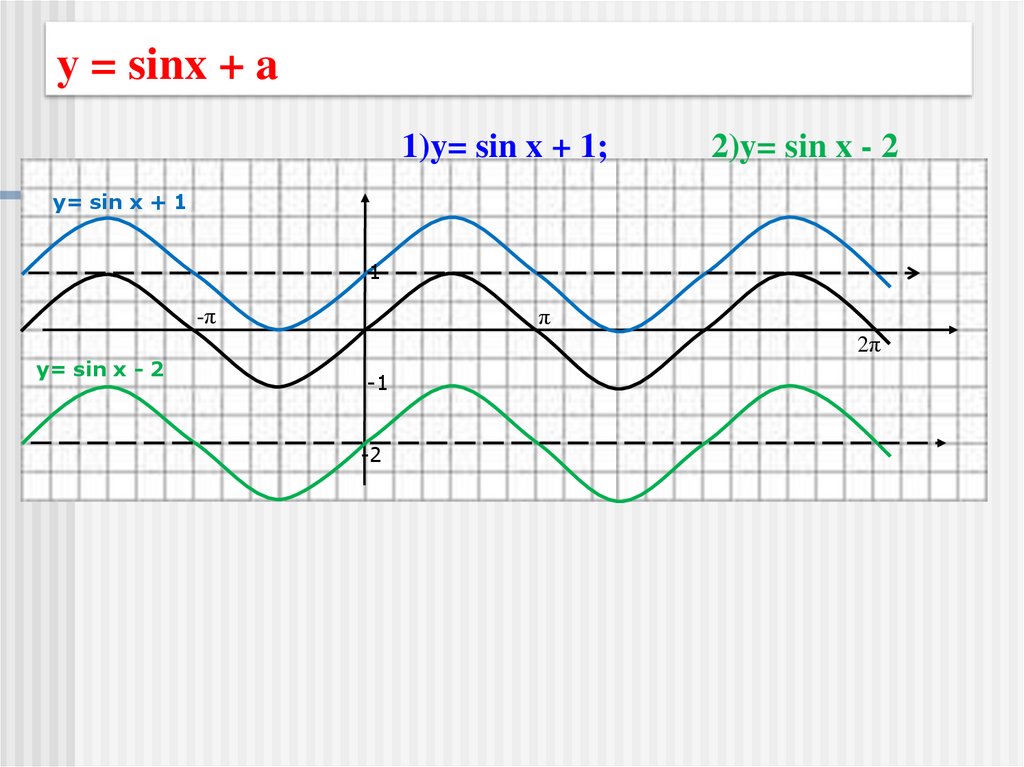
График функции у = f (x)+a получается из
графика функции у = f(x) параллельным
переносом на (a) единиц вдоль оси ординат
6

7. у = sin(x+a)

y = sin(x+π/6)
1
π
-π
2π
-1

8. у = sinx + a

1)y= sin x + 1;
2)y= sin x - 2
y= sin x + 1
1
π
-π
y= sin x - 2
2π
-1
-2

9.

Преобразование графиков
тригонометрических функций путем
сжатия и растяжения
График функции у =k f (x) получается из
графика функции у = f(x) путем его
растяжения в k раз (при k>1) вдоль оси ординат
График функции у = k f (x) получается из
графика функции у = f(x) путем его сжатия в k
раз (при 0<k<1) вдоль оси ординат
9

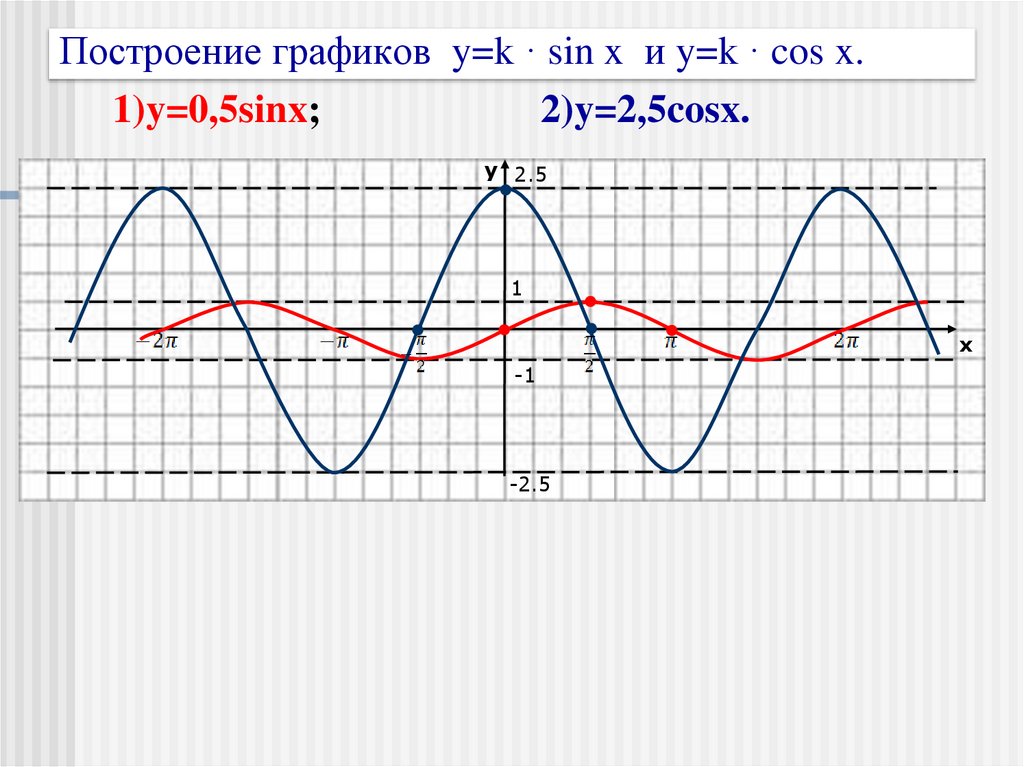
10. Построение графиков y=k · sin x и y=k · cos x.

1)y=0,5sinx;
2)y=2,5cosx.
y 2.5
1
x
-1
-2.5

11.

Преобразование графиков
тригонометрических функций путем
сжатия и растяжения
График функции у = f (kx) получается из
графика функции у = f(x) путем его сжатия в k
раз (при k>1) вдоль оси абсцисс
График функции у = f (kx) получается из
графика функции у = f(x) путем его
растяжения в k раз (при 0<k<1) вдоль оси
абсцисс
11

12. Периодичность

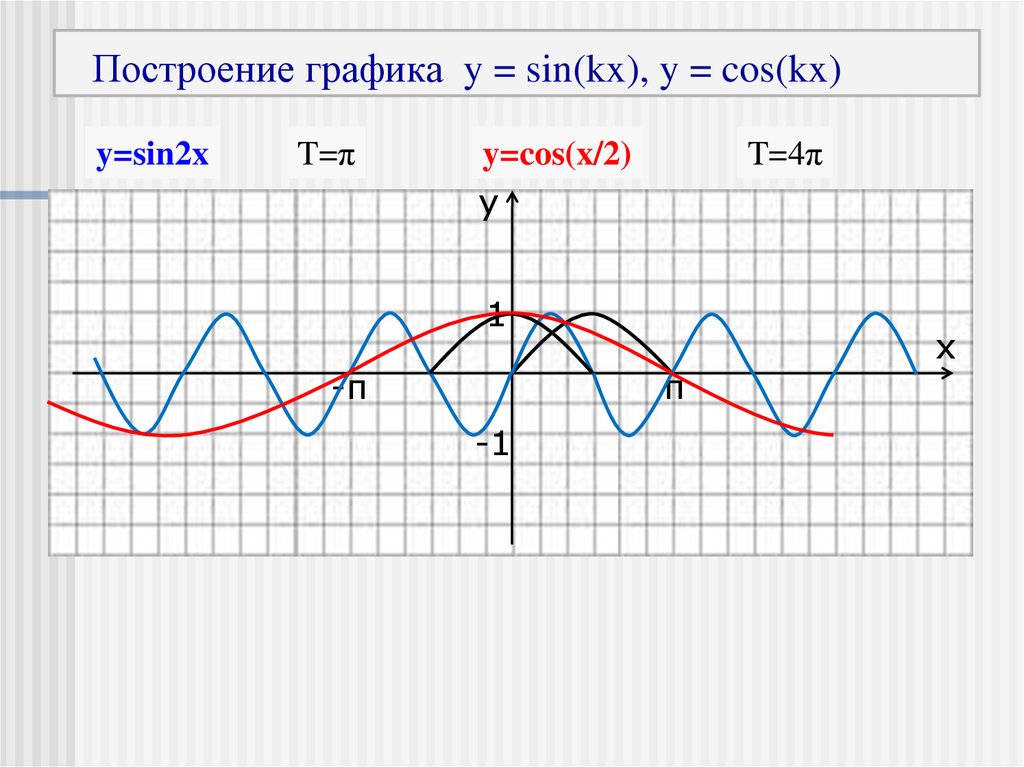
13. Построение графика y = sin(kx), y = cos(kx)

y=sin2x
T=π
y=cos(x/2)
у
T=4π
1
-π
π
-1
х

14.

Преобразование графиков
тригонометрических функций путем
сжатия и растяжения
Графики функций у = -f (kx) и у=-k f(x)
получаются из графиков функций у = f(kx) и
y= k f(x) соответственно путем их зеркального
отображения относительно оси абсцисс
синус – функция нечетная, поэтому
sin(-kx) = - sin (kx)
косинус –функция четная, значит
cos(-kx) = cos(kx)
14

15.

Преобразование графиков
тригонометрических функций путем
сжатия и растяжения
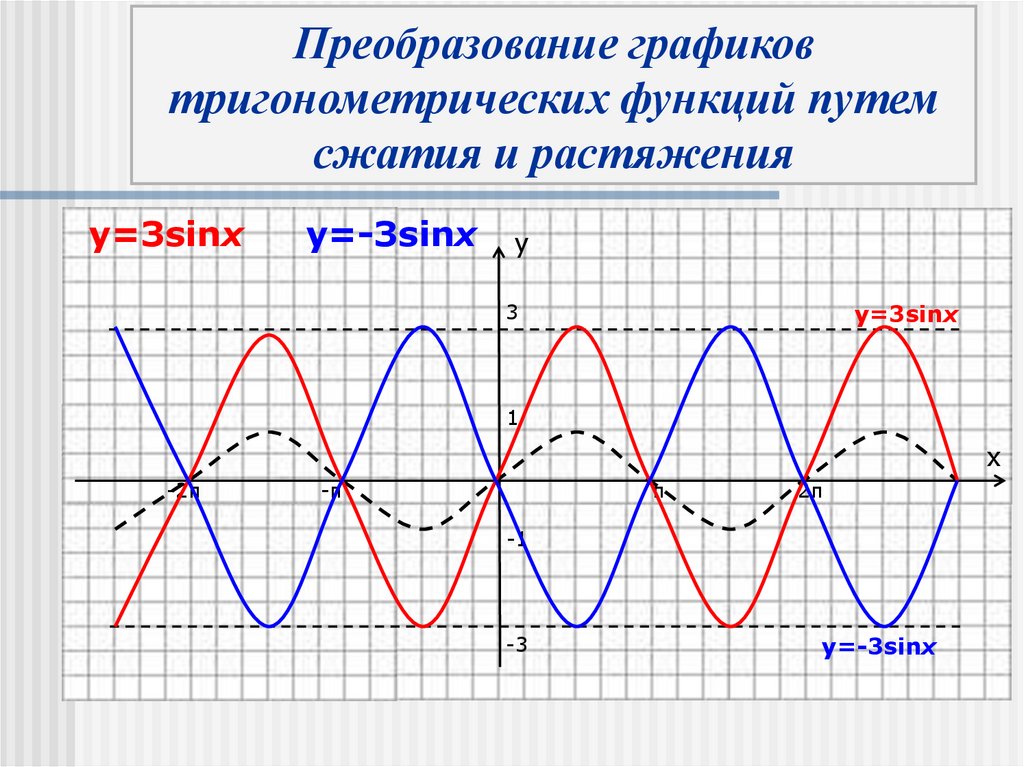
y=3sinx
y=-3sinx
y
y=3sinx
3
1
x
-2π
-π
π
2π
-1
-3
y=-3sinx

16.

Преобразование графиков
тригонометрических функций путем
сжатия и растяжения
y
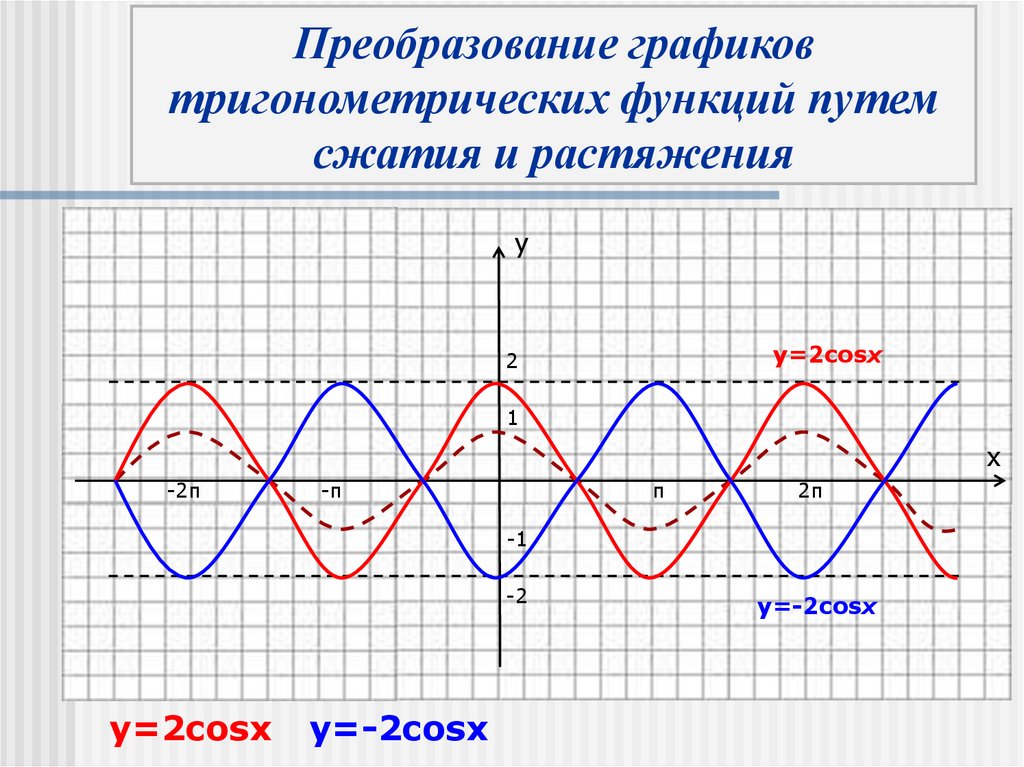
y=2cosx
2
1
x
-2π
-π
π
2π
-1
-2
y=2cosx
y=-2cosx
y=-2cosx

17.

Преобразование графиков
тригонометрических функций путем
сжатия и растяжения
График функции у = f (kx+b) получается из
графика функции у = f(x) путем его
параллельного переноса на (-b/k) единиц вдоль
оси абсцисс и путем сжатия в k раз (при k>1)
или растяжения в k раз ( при 0<k<1) вдоль оси
абсцисс
f ( kx+b) = f ( k( x+b/k))
17

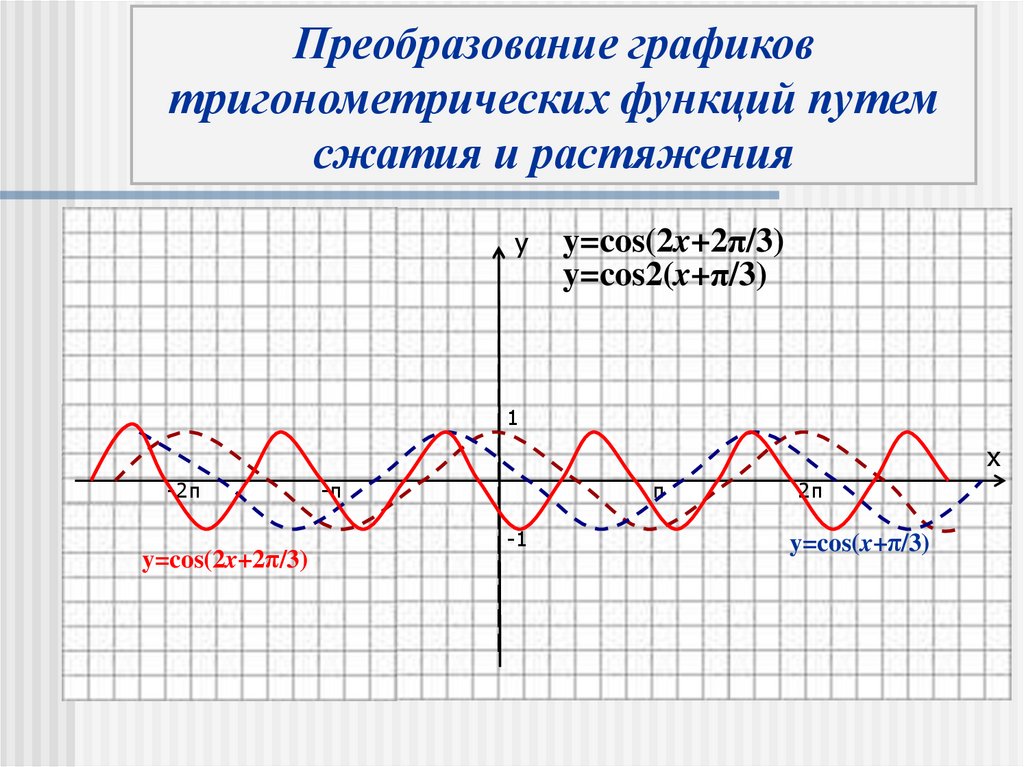
18.

Преобразование графиков
тригонометрических функций путем
сжатия и растяжения
y
y=cos(2x+2π/3)
y=cos2(x+π/3)
1
x
-2π
y=cos(2x+2π/3)
-π
π
-1
2π
y=cos(x+π/3)

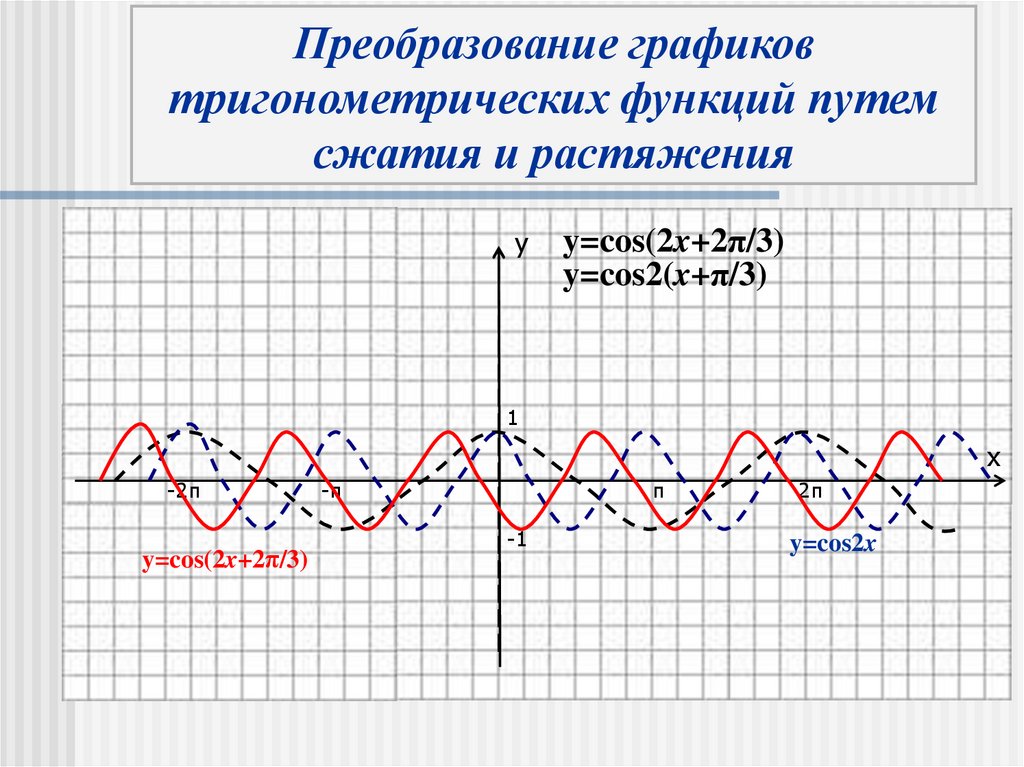
19.

Преобразование графиков
тригонометрических функций путем
сжатия и растяжения
y
y=cos(2x+2π/3)
y=cos2(x+π/3)
1
x
-2π
y=cos(2x+2π/3)
-π
π
-1
2π
y=cos2x

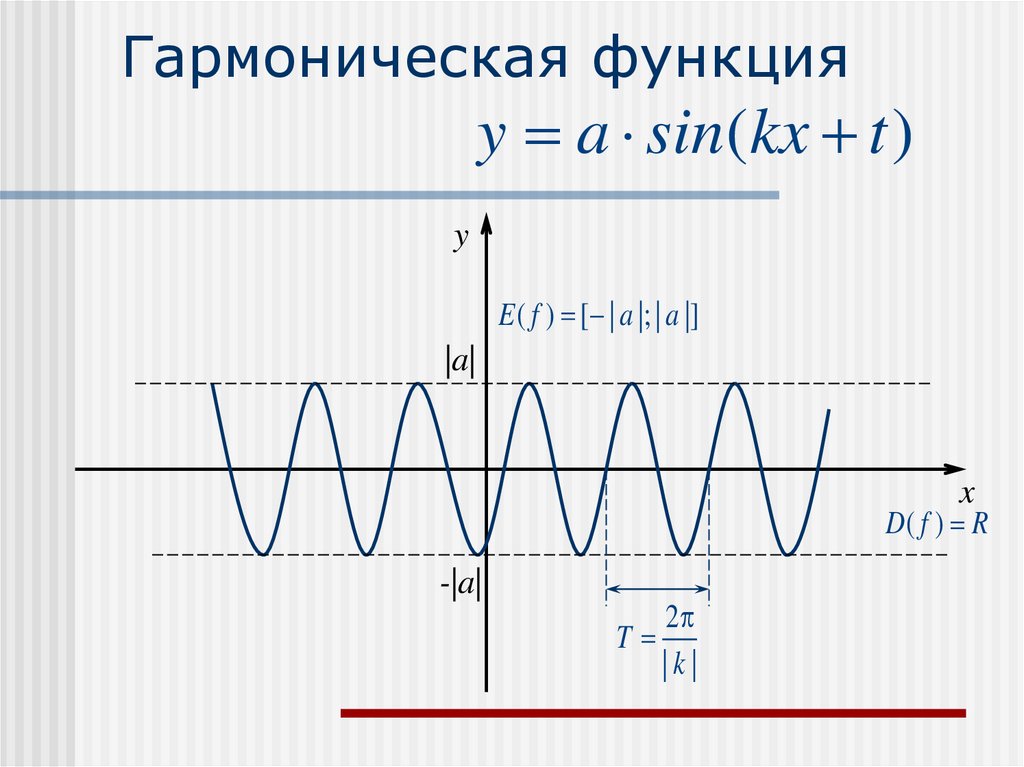
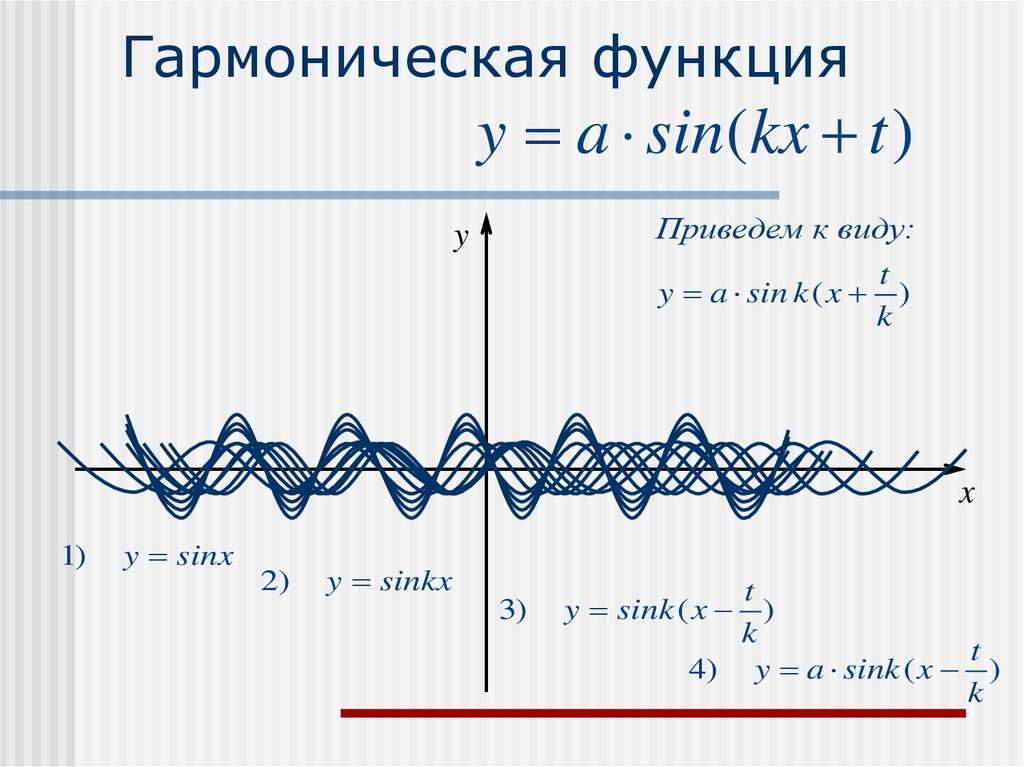
20. Гармоническая функция

y a sin(kx t )
y
E ( f ) [ | a |; | a |]
|a|
x
D( f ) R
-|a|
T
2
|k|

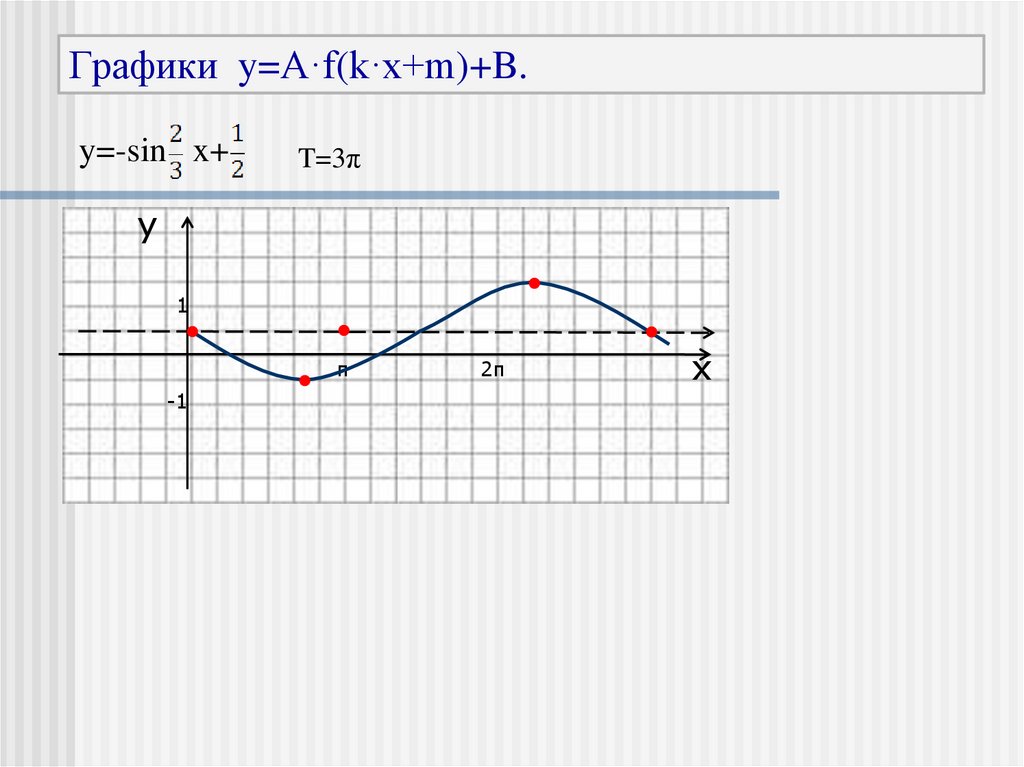
21. Графики y=A·f(k·x+m)+B.

y=-sin x+
T=3π
y
1
π
-1
2π
x

22. Гармоническая функция

y a sin(kx t )
Приведем к виду:
t
y a sin k ( x )
k
y
x
1)
y sinx
2)
y sinkx
3)
t
)
k
t
4) y a sink ( x )
k
y sink ( x

23. Загадка урока

Что общего между:
качелями
музыкой
и светом
это колебательные
процессы, которые
описываются с помощью
гармонической функции:
y a sin(kx t )

24. Загадка урока

Подними качели повыше – изменишь t (фазу) механических
колебаний.
Включи полную громкость – увеличишь a (амплитуду)
колебаний воздуха.
Добавь красного цвета в палитру – уменьшишь k
(частоту) электромагнитных колебаний.
y a sin(kx t )

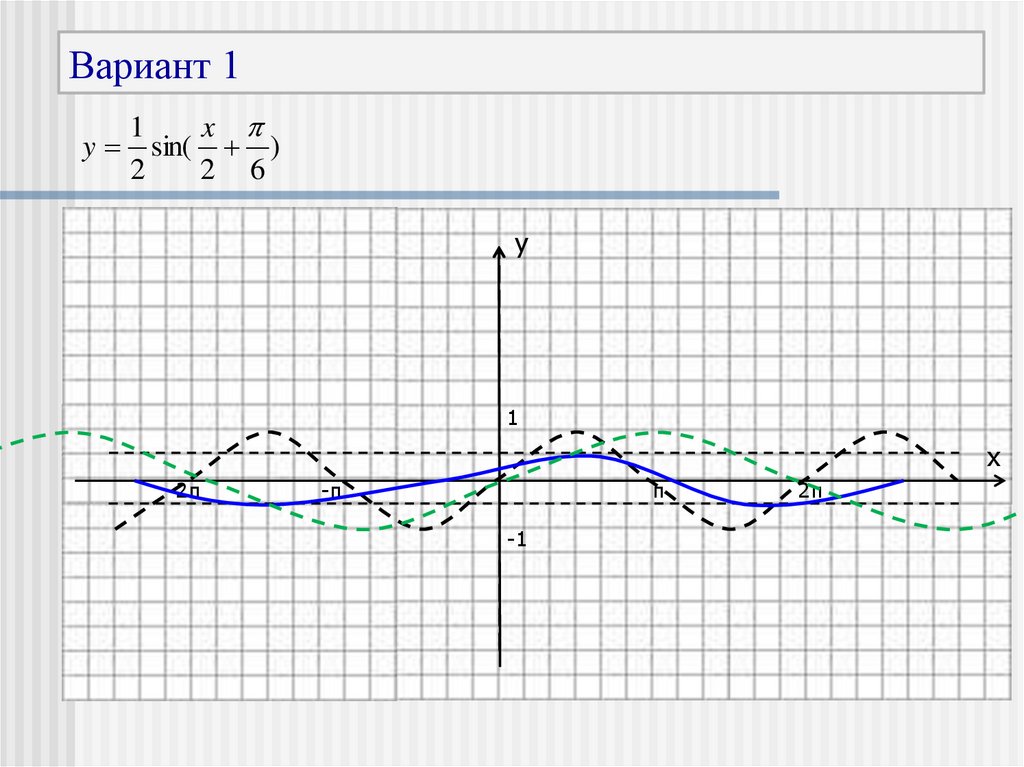
25. Вариант 1

y
1
x
sin( )
2
2 6
y
1
x
-2π
-π
π
-1
2π

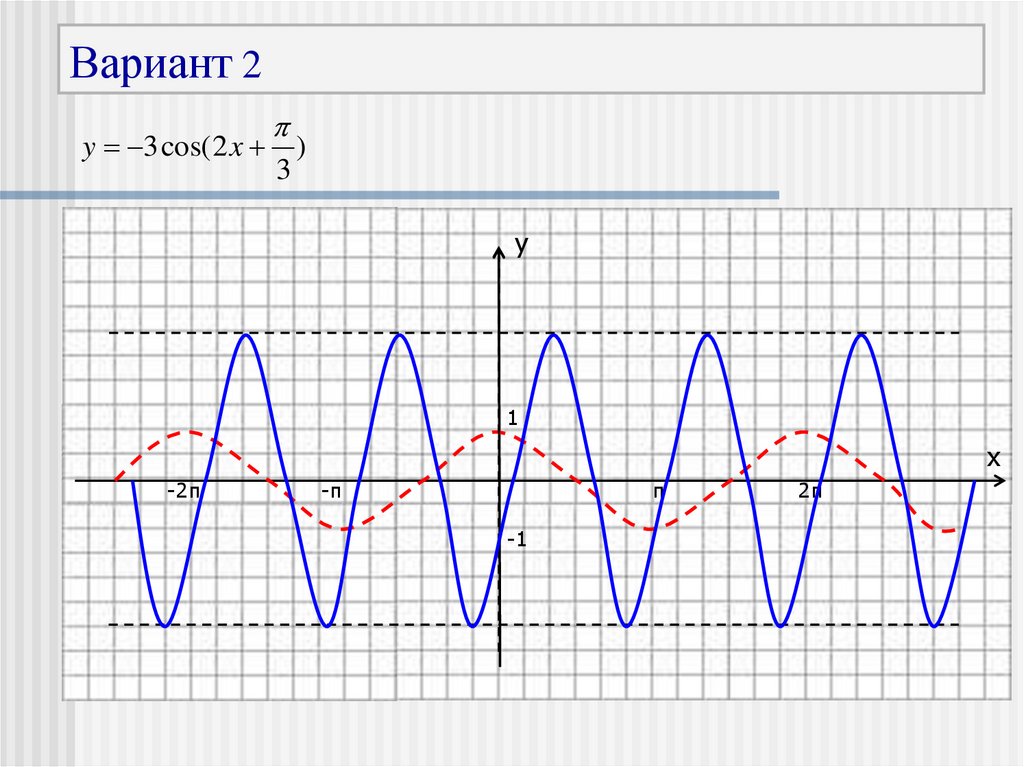
26.

Вариант 2
y 3 cos( 2 x
3
)
y
1
x
-2π
-π
π
-1
2π

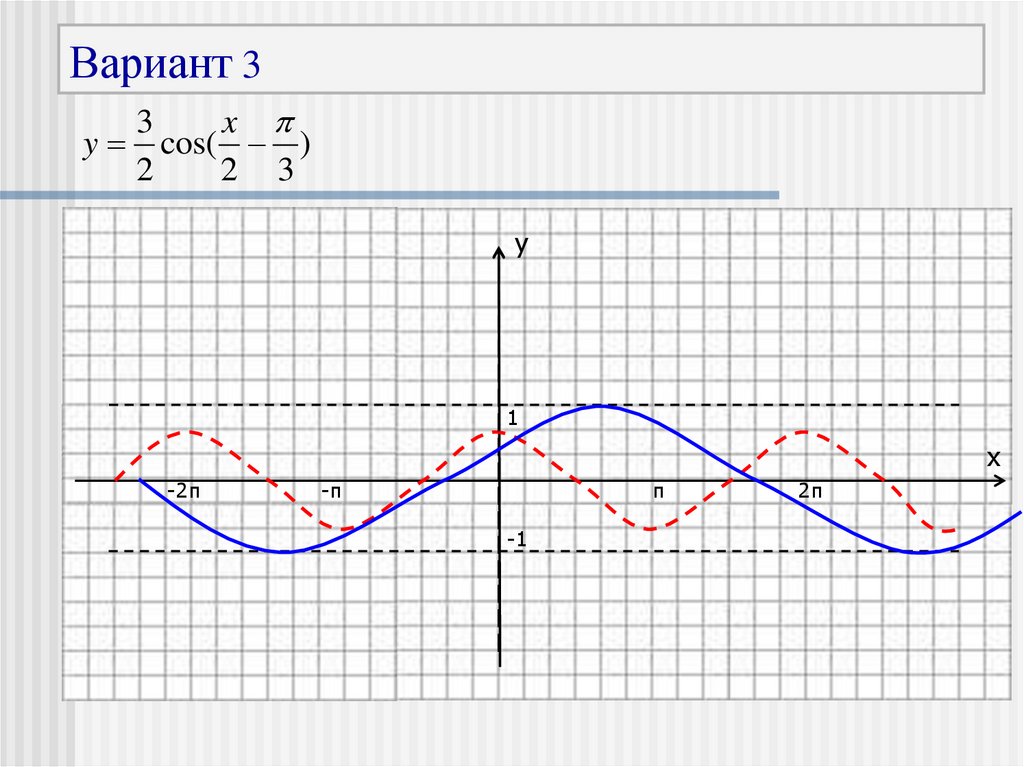
27.

Вариант 3
3
x
y cos( )
2
2 3
y
1
x
-2π
-π
π
-1
2π

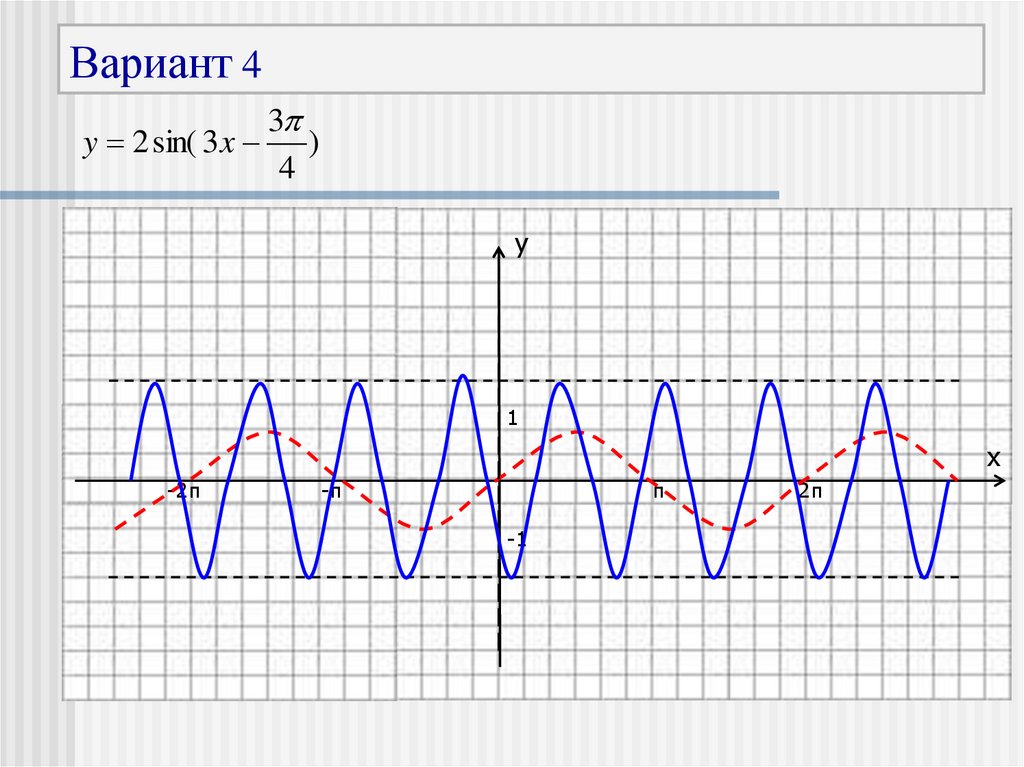
28.

Вариант 4
3
y 2 sin( 3 x )
4
y
1
x
-2π
-π
π
-1
2π

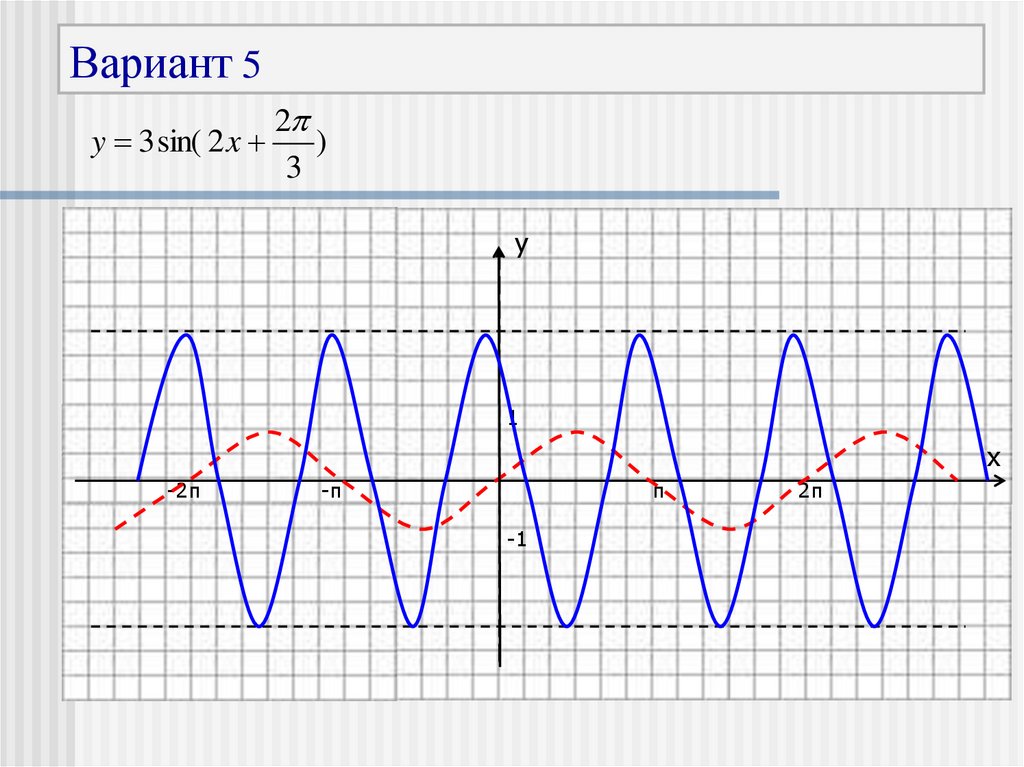
29.

Вариант 5
y 3 sin( 2 x
2
)
3
y
1
x
-2π
-π
π
-1
2π

30.

Спасибо за
внимание