Копия Корень п-й ст.из действ.числа 18.11.25

1.

Определение корня
n-ой степени
n
а
10 класс

2.

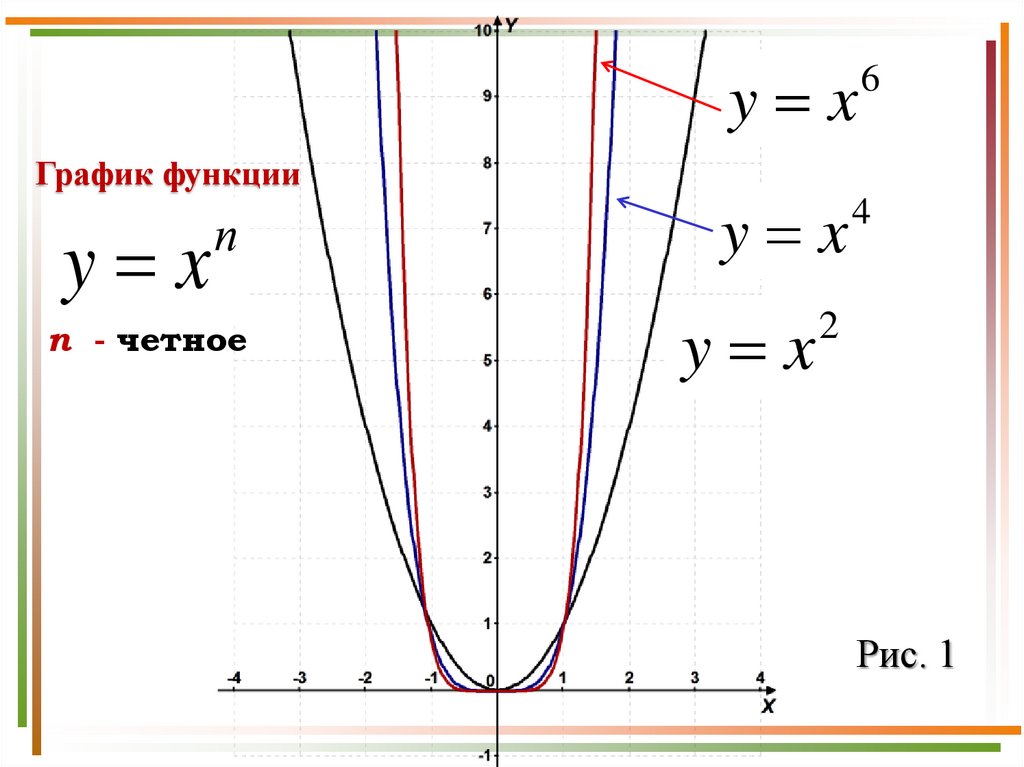
y x
График функции
y x
п
n - четное
y x
y x
6
4
2
Рис. 1

3.

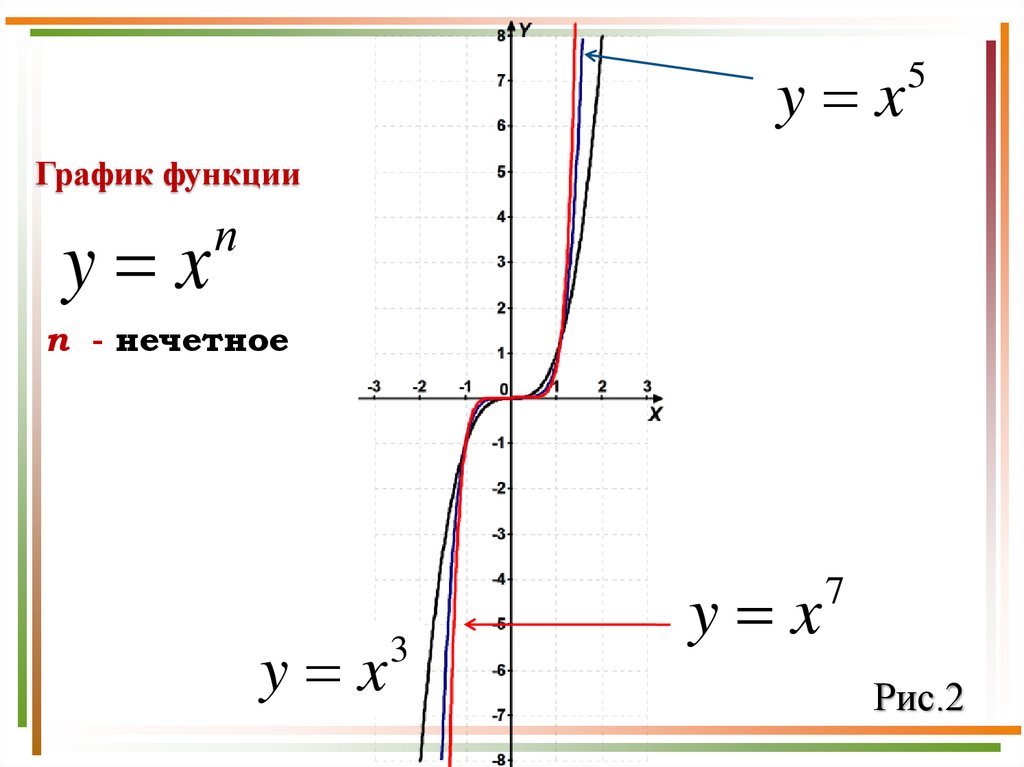
y x
5
График функции
y x
п
n - нечетное
y x
3
y x
7
Рис.2

4. Решить графически уравнение

4
x 1
Алгоритм графического решения уравнения
1. Рассмотреть функции левой и правой части
уравнения.
2. Построить в одной системе координат
график функции у = х⁴ и прямую у = 1.
3. Найти координаты точек пересечения
4. Абсциссы точек пересечения являются
корнями данного уравнения

5.

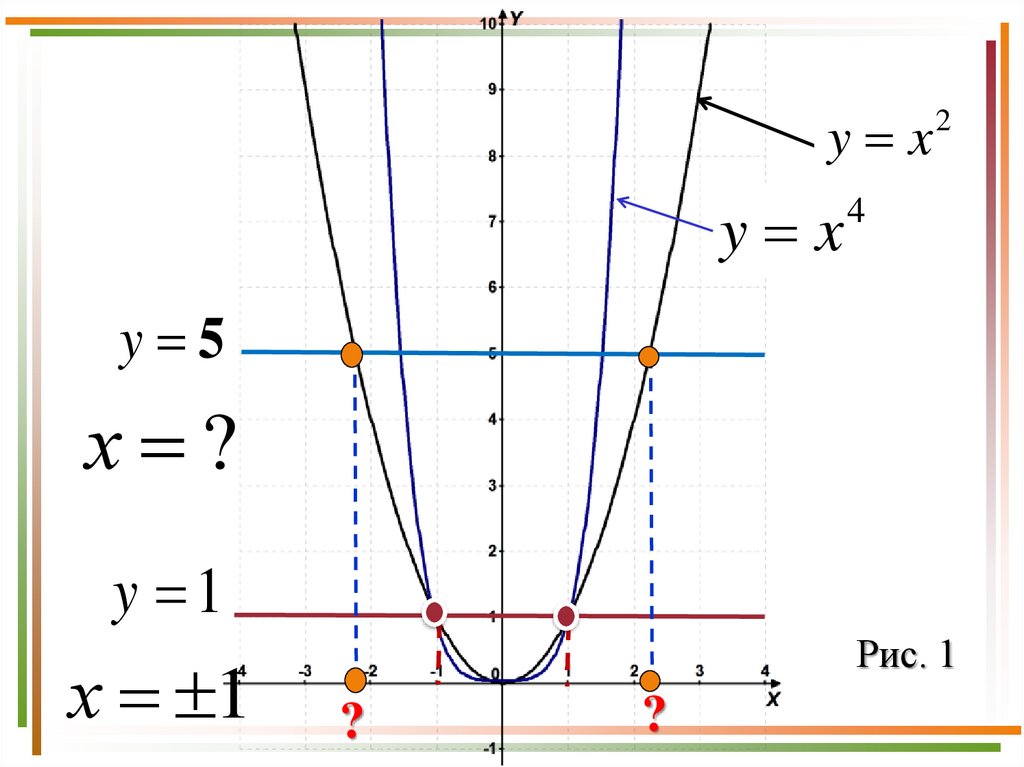
y x
y x
2
4
y 5
х ?
y 1
х 1
Рис. 1
?
?

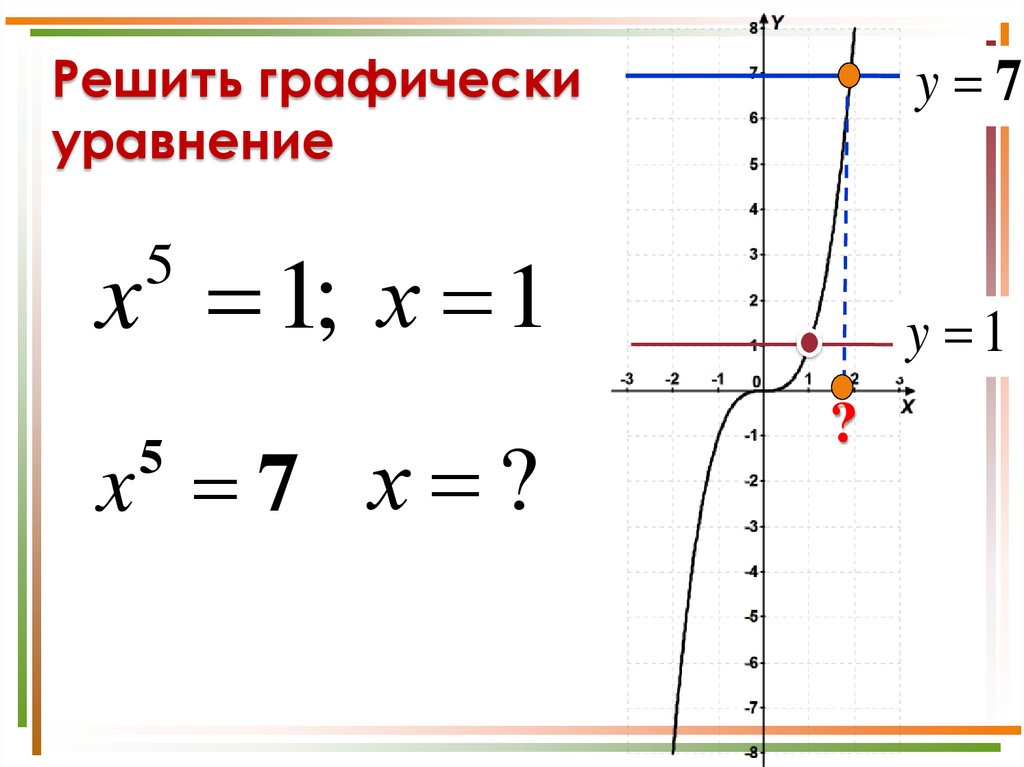
6. Решить графически уравнение

y 7
Решить графически
уравнение
x 1; х 1
5
x 7 х ?
5
y 1
?

7. Проблема!

• Возникает новое понятие,n
появляется новый символ а
• Решение уравнений:
x 5
x 7
два корня
один корень
4
4
5 и 5
4
5
5
7

8. Определение корня n-ой степени

Корнем n-й степени из числа а (n = 2, 3, 4,
5, ...) называют такое число,
п-я степень которого равна а.
n
a b, b a, где n N, n 1
n
Число а называют подкоренным числом,
а число n – показателем корня

9.

10.

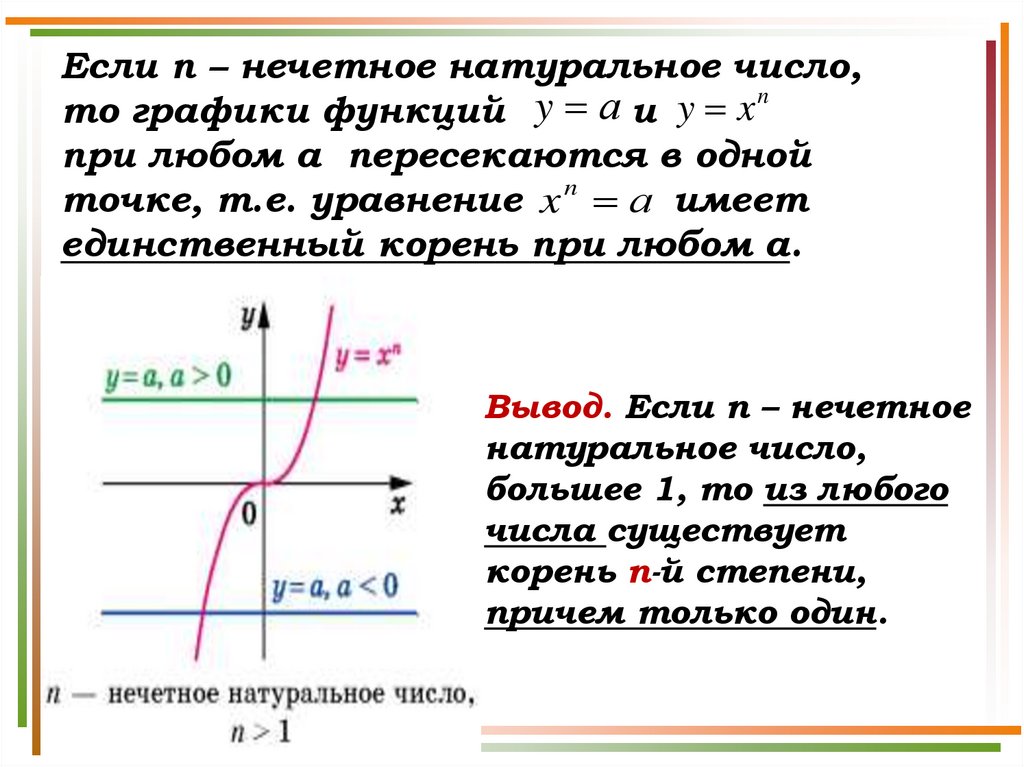
Если n – нечетное натуральное число,
n
то графики функций y а и y x
при любом а пересекаются в одной
точке, т.е. уравнение x n а имеет
единственный корень при любом а.
Вывод. Если n – нечетное
натуральное число,
большее 1, то из любого
числа существует
корень п-й степени,
причем только один.

11. Примеры

1)
3
2)
3
3)
5
4)
3
27 3;
( 3 ) 27
64000 40;
403 64000
0,00243 0,3;
0,3 0,00243
1000000 100;
( 1003 ) 1000000
3
5
Примечание:
Принято корень третьей степени называть –
кубическим корнем.

12. Запомните!

• Корень нечетной степени
имеет смысл для любого
подкоренного числа, т.е. при
любом а выполняется
равенство
(
2k 1
a)
2k 1
a
• Например:
( 27 ) 27, ( 0,1) 0,1
3
3
7
7

13.

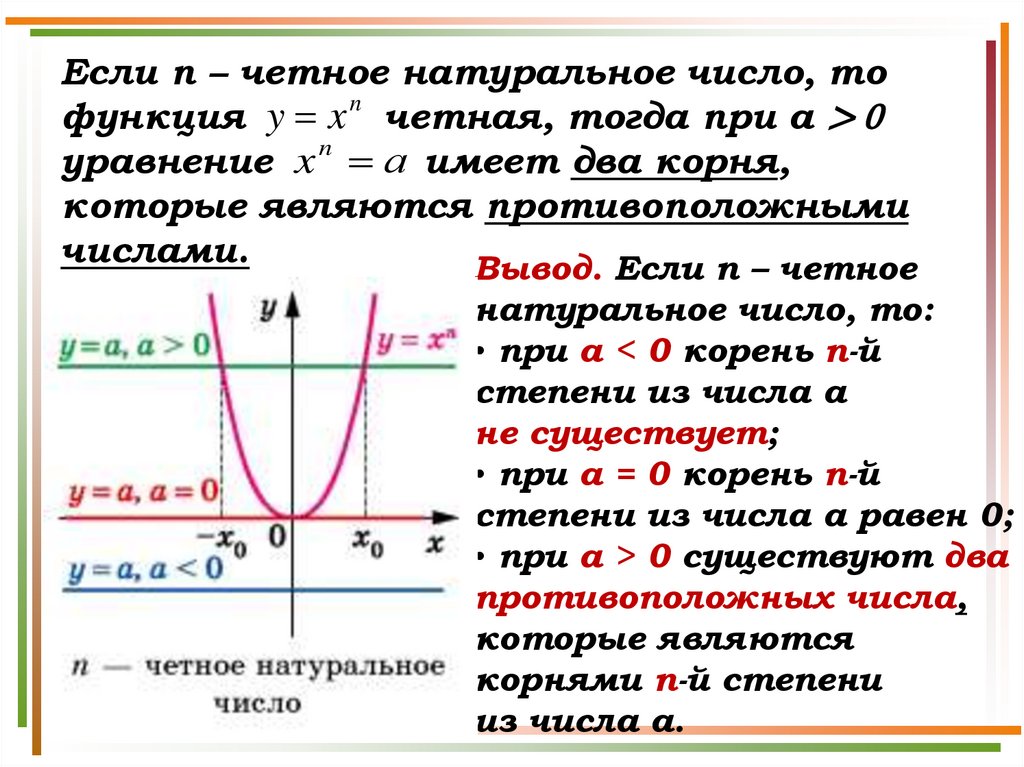
Если n – четное натуральное число, то
функция y x n четная, тогда при а > 0
уравнение x n а имеет два корня,
которые являются противоположными
числами.
Вывод. Если n – четное
натуральное число, то:
• при а < 0 корень п-й
степени из числа а
не существует;
• при а = 0 корень п-й
степени из числа а равен 0;
• при а > 0 существуют два
противоположных числа,
которые являются
корнями п-й степени
из числа а.

14. Определение

Арифметическим корнем n-й степени
из неотрицательного числа а (n = 2, 3, 4, 5,
...) называют такое неотрицательное
число, п-я степень которого равна а.
n
a b - арифметиче ский корень из числа а,
если b n a, где a 0, b 0, n N, n 1.
Из определения следует:
n
a 0, где а 0
Корень нечетной степени
из отрицательного числа
можно выразить через
арифметический корень:
( a ) a, где а 0
n
n
2k 1
-a -
2k 1
a

15. Запомните!

• Корень четной степени имеет
смысл (т.е. определен) только
для неотрицательного
подкоренного числа.
• Корень нечетной степени
имеет смысл для любого
подкоренного числа.

16. Примеры

1)
6
1 1
1
1 6 1
, т.к. 0 и ( ) ;
64 2
2
2
64
2)
4
256 4, т.к. 4 0 и 4 256;
3)
10
4)
3
4
0 0, т.к. 0 0 и 0 0;
27 3 27 3;
10

17.

Выпишите выражения,
которые не имеют смысла?
1; 4 ; 8 ; 27 ; 1; 4 5 ; 8 ;
3
4
3
3
16 ; 1; 27 ; 9 ; 16 ; 1;
3
3
4
8
4 ; 9 ; 32
3
5
№ 11.1, 3, 9
1.Дома: § 11 – вопросы 1-2,
выучить определения, № 11.2, 4, 10
§ 12 – изучить, выписать свойства

18. Можно ли извлечь корень п-й степени из отрицательного числа?

• Можно, но только в случае
нечетного показателя корня!
Корнем нечетной степени п
из отрицательного числа а (n = 3, 5, ...)
называют такое отрицательное число,
при возведении которого в степень п
получается число а.