https___school.mos.ru_ej_attachments_files_218_707_344_original_7D0D0D0D0D1D0D1D020BF80B8B7BDB0BAD1D0D0D0D0D1D1D0

1.

1

2.

Практическое задание
• Отметьте в тетради любые три точки: А, В, С.
• Соедините их отрезками.
• Какая геометрическая фигура получилась?

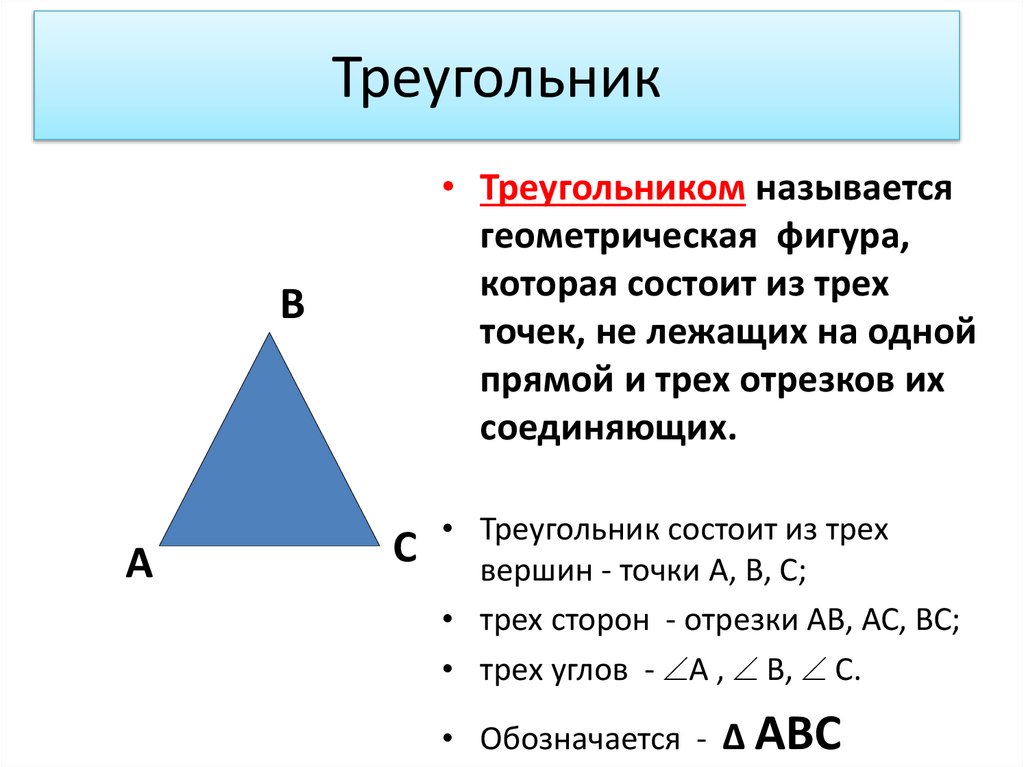
3. Треугольник

• Треугольником называется
геометрическая фигура,
которая состоит из трех
точек, не лежащих на одной
прямой и трех отрезков их
соединяющих.
В
А
С
• Треугольник состоит из трех
вершин - точки А, В, С;
• трех сторон - отрезки АВ, АС, ВС;
• трех углов - А , В, С.
• Обозначается - ∆ АВС

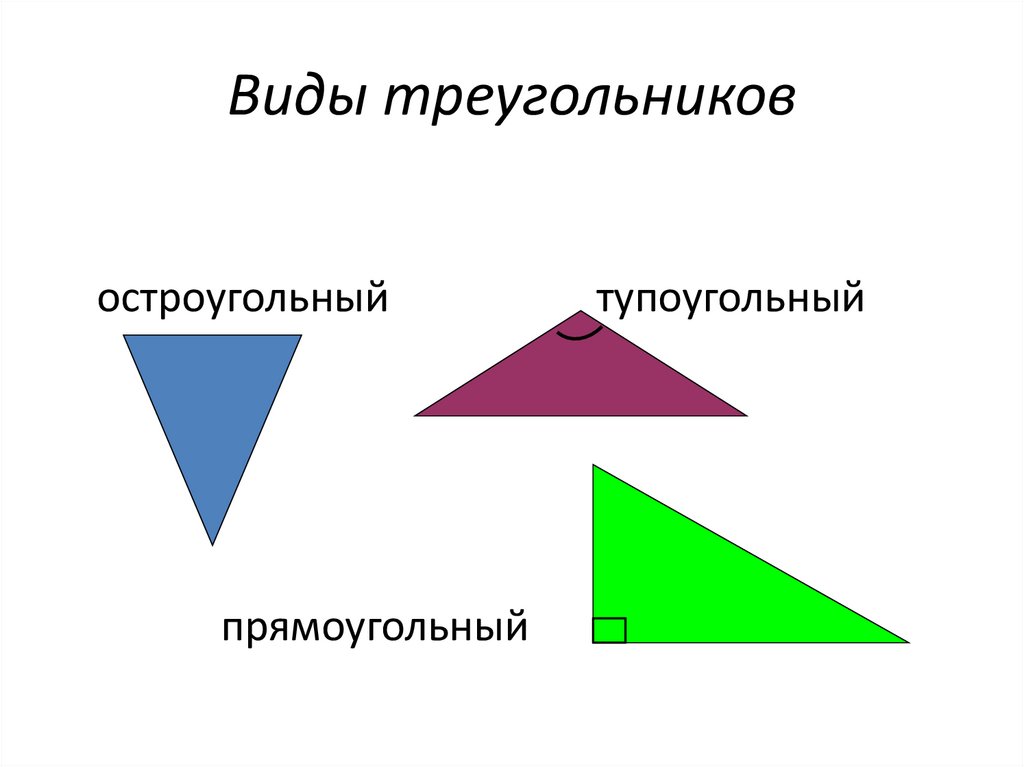
4. Виды треугольников

остроугольный
прямоугольный
тупоугольный

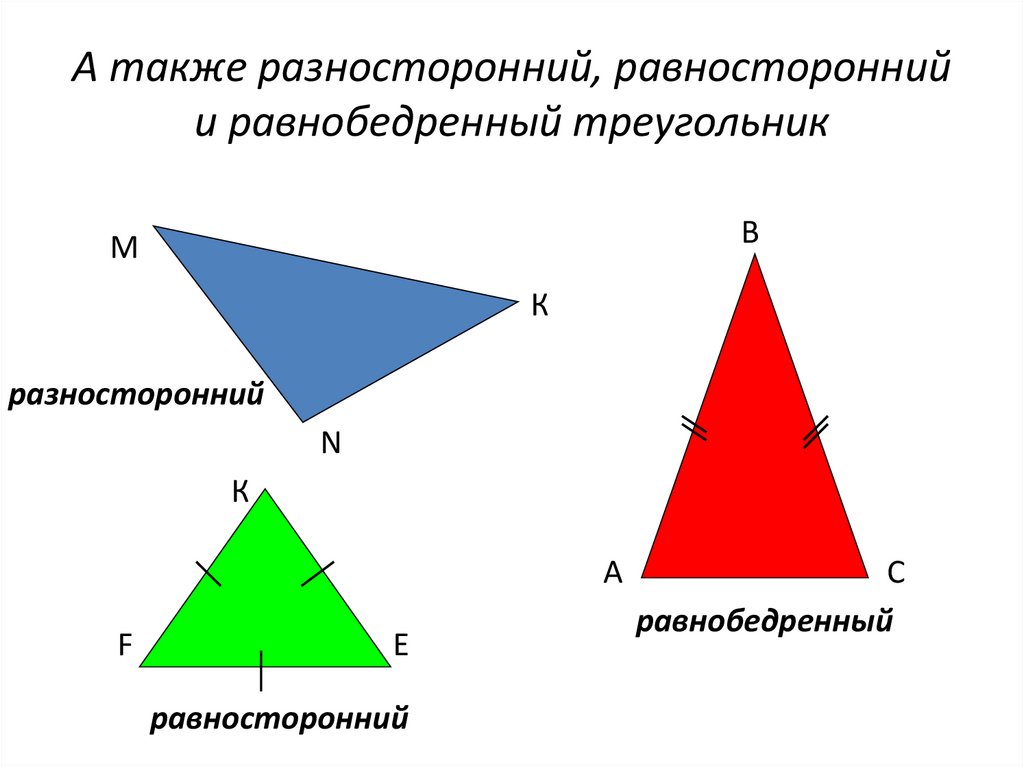
5. А также разносторонний, равносторонний и равнобедренный треугольник

В
М
К
разносторонний
N
К
А
F
Е
равносторонний
С
равнобедренный

6.

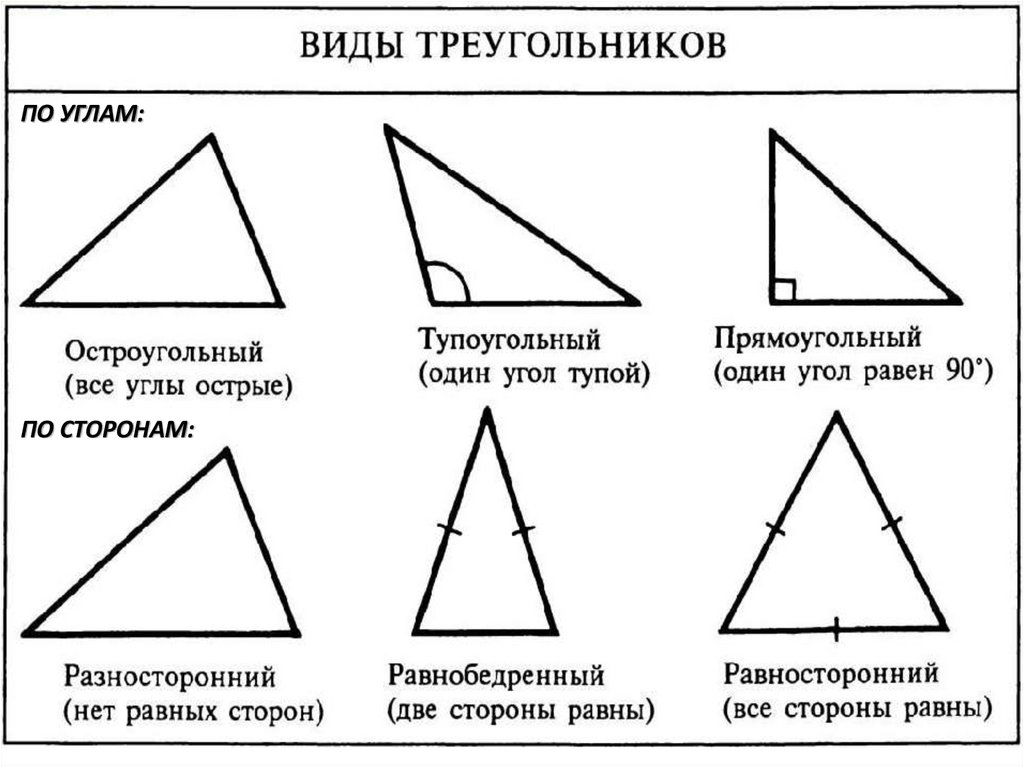
ПО УГЛАМ:
ПО СТОРОНАМ:
19.09.2012
www.konspekturoka.ru
6

7.

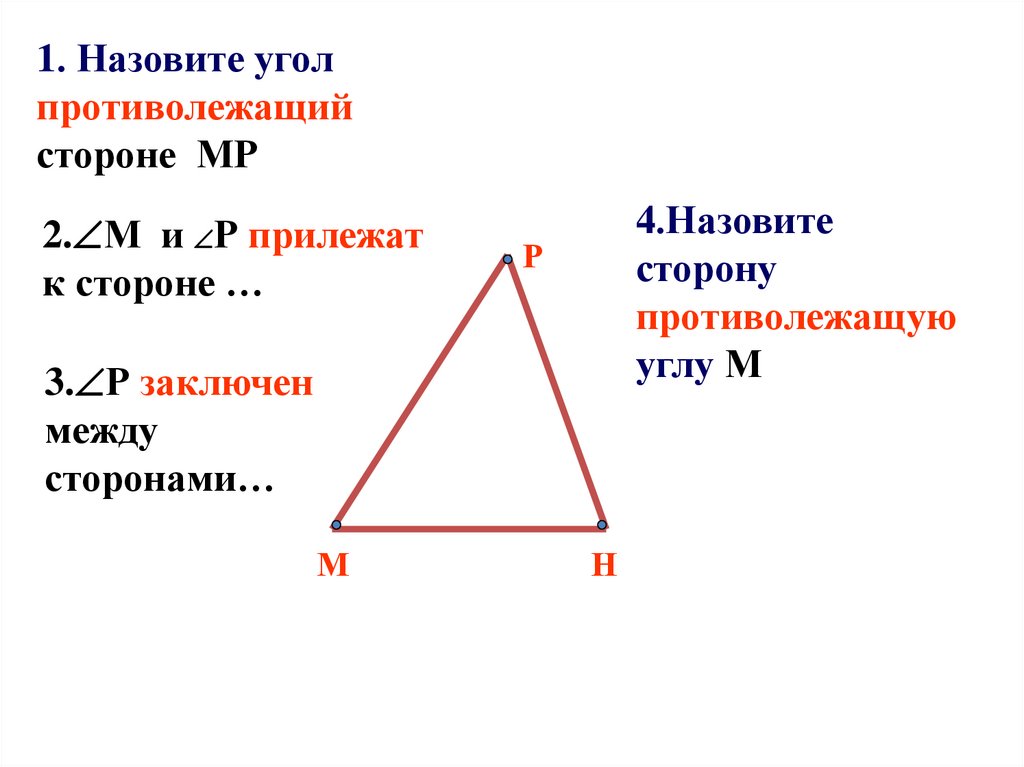
1. Назовите угол
противолежащий
стороне МР
2. М и Р прилежат
к стороне …
4.Назовите
сторону
противолежащую
углу М
Р
3. Р заключен
между
сторонами…
М
Н

8.

А
С
С₁
А₁
В
В₁
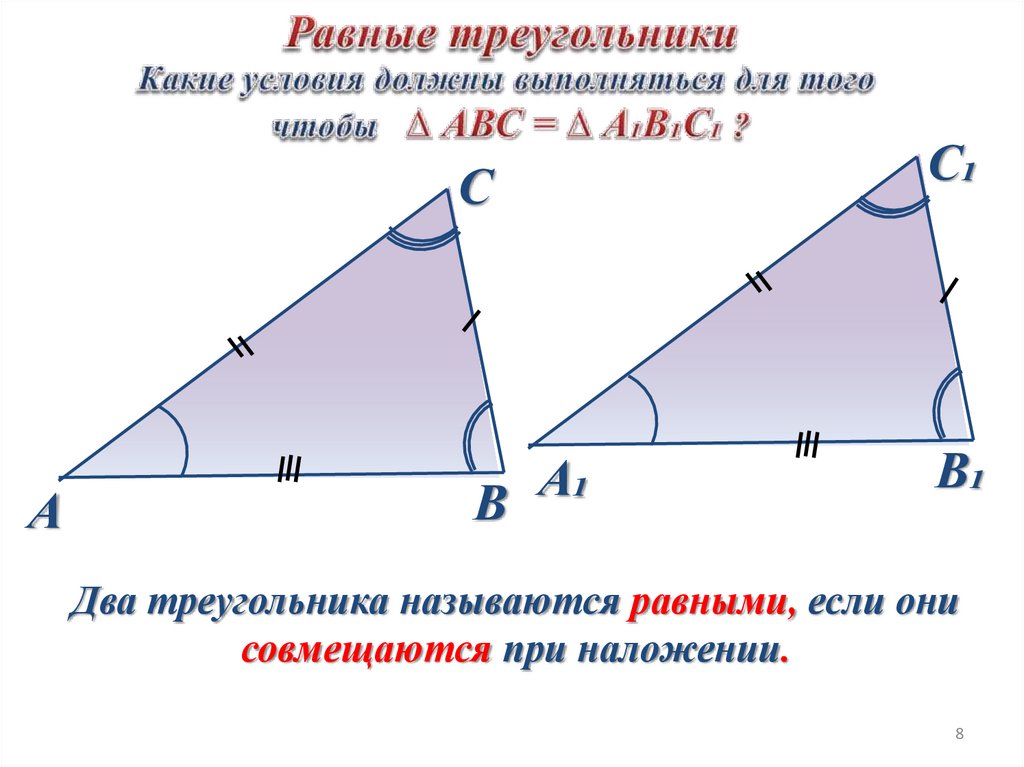
Два треугольника называются равными, если они
совмещаются при наложении.
8

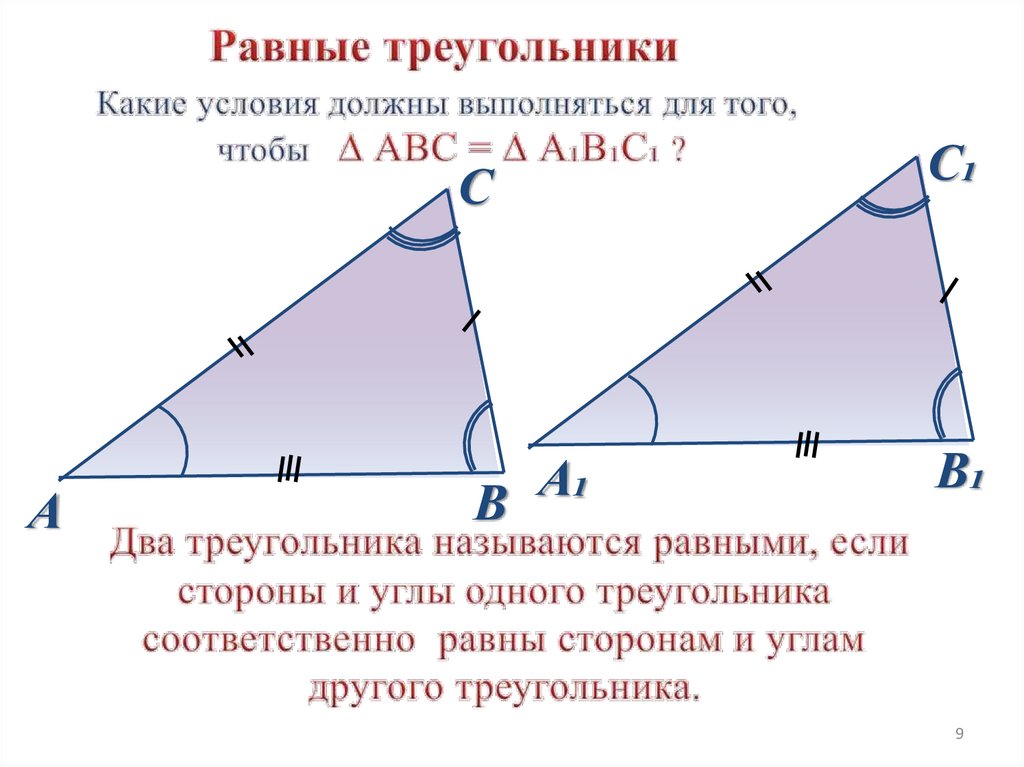
9.

А
С
С₁
А₁
В
В₁
9

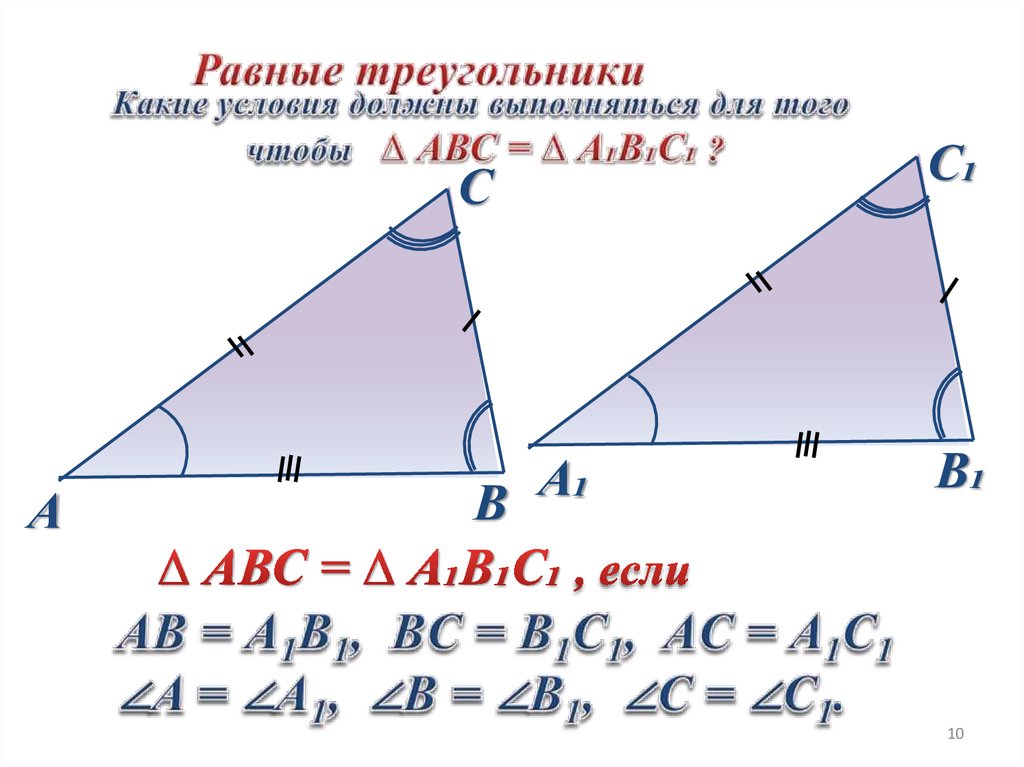
10.

А
С
С₁
А₁
В
В₁
10

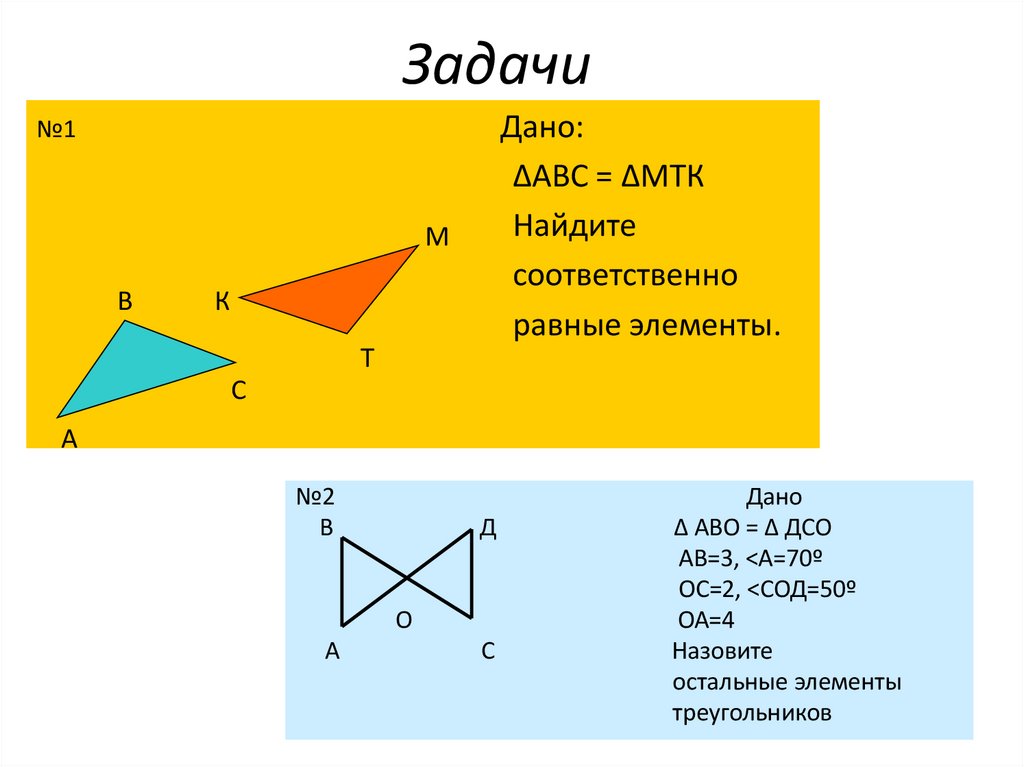
11. Задачи

Дано:
∆АВС = ∆МТК
Найдите
соответственно
равные элементы.
№1
М
В
К
Т
С
А
№2
В
Д
О
А
С
Дано
∆ АВО = ∆ ДСО
АВ=3, <А=70º
ОС=2, <СОД=50º
ОА=4
Назовите
остальные элементы
треугольников

12.

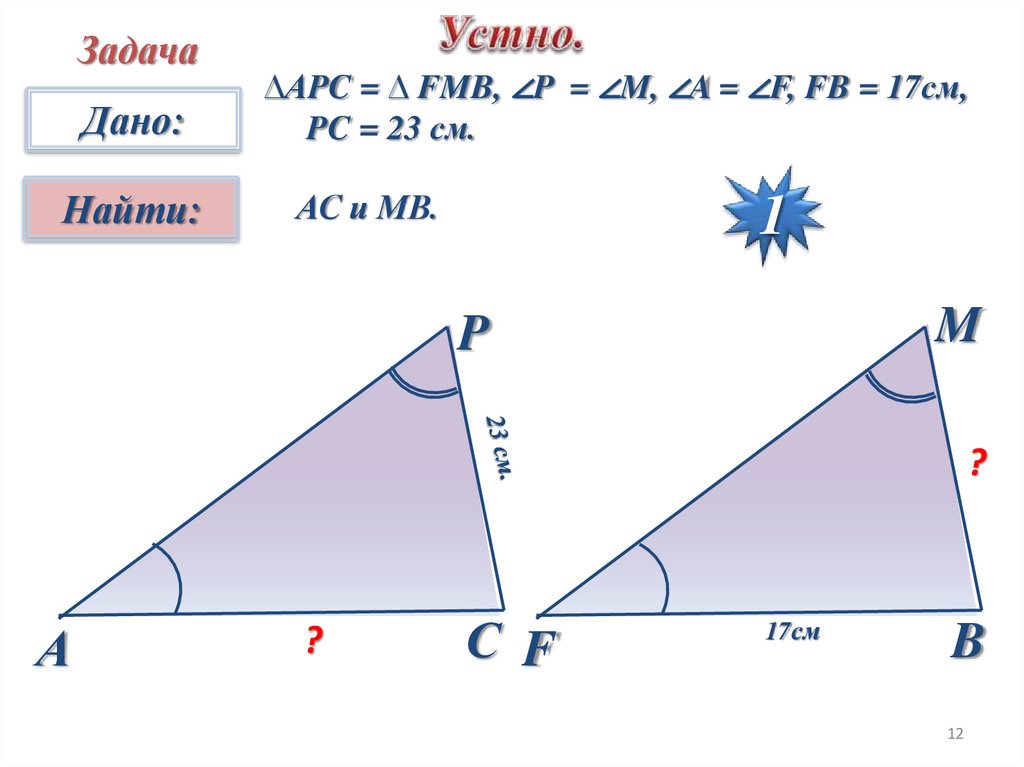
Задача
Дано:
Найти:
∆АPC = ∆ FMB, ∠P = ∠M, ∠A = ∠F, FB = 17см,
PC = 23 см.
АС и МВ.
1
M
P
?
А
?
С F
17см
B
12

13.

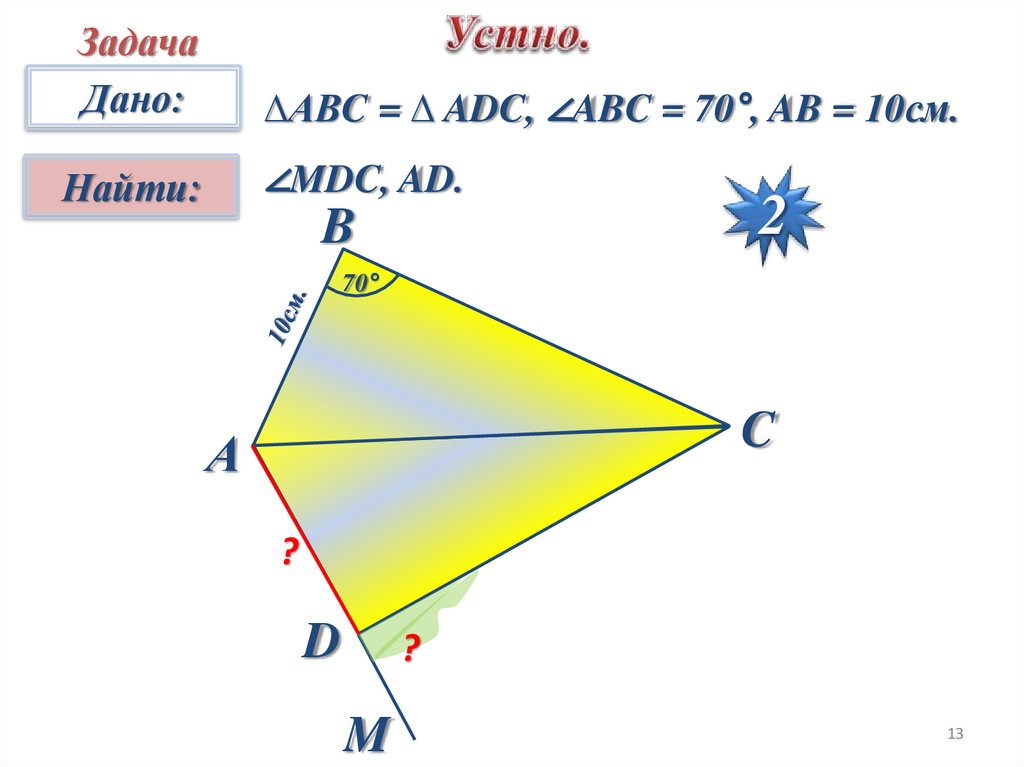
Задача
Дано:
∆АВC = ∆ ADC, ∠ABC = 70°, AB = 10см.
Найти:
∠MDC, AD.
B
2
70°
C
А
?
D
?
M
13

14.

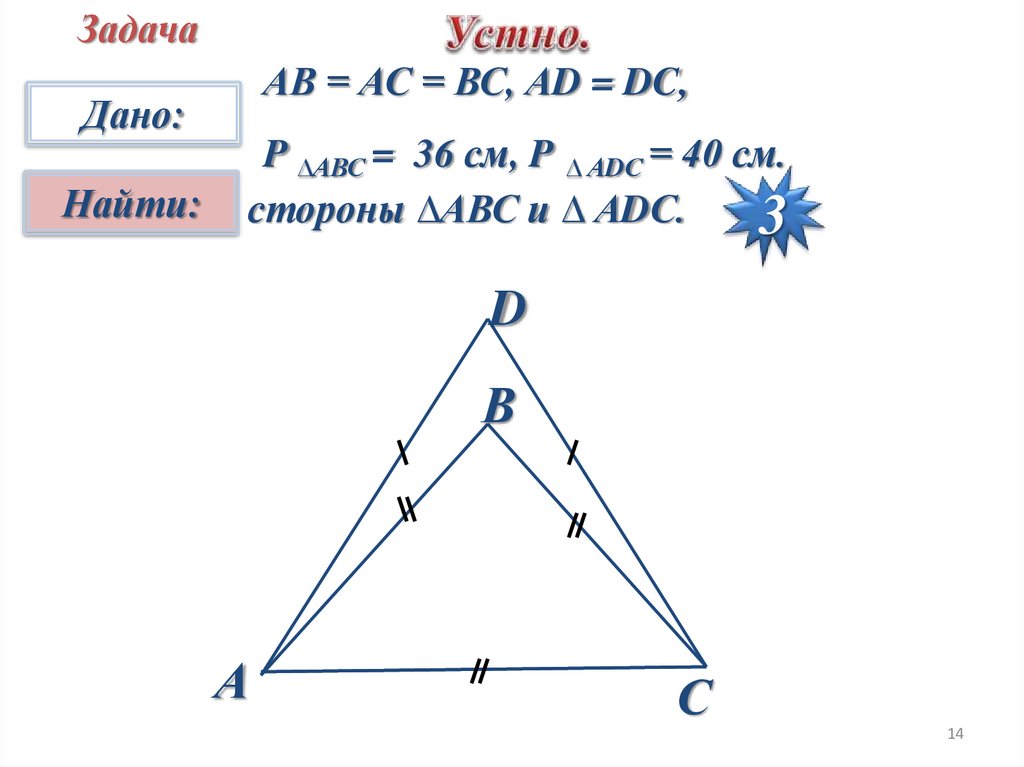
Задача
Дано:
Найти:
АВ = АС = ВС, АD = DC,
P ∆АВС = 36 см, P ∆ АDС = 40 см.
стороны ∆АВС и ∆ АDС.
3
D
В
А
С
14

15.

15

16.

Доказывать признаки нужно с помощью
теоремы - это утверждение,
справедливость которого
устанавливается путем рассуждений).
Сами рассуждения называются
доказательством теоремы.
Любая теорема состоит из условия
и заключения.
Условие – это уже известные факты, о которых
говорится в теореме (ДАНО), а заключение – это то,
что нужно получить, доказать (ДОКАЗАТЬ).
16

17.

Первый признак
равенства
треугольников
17

18.

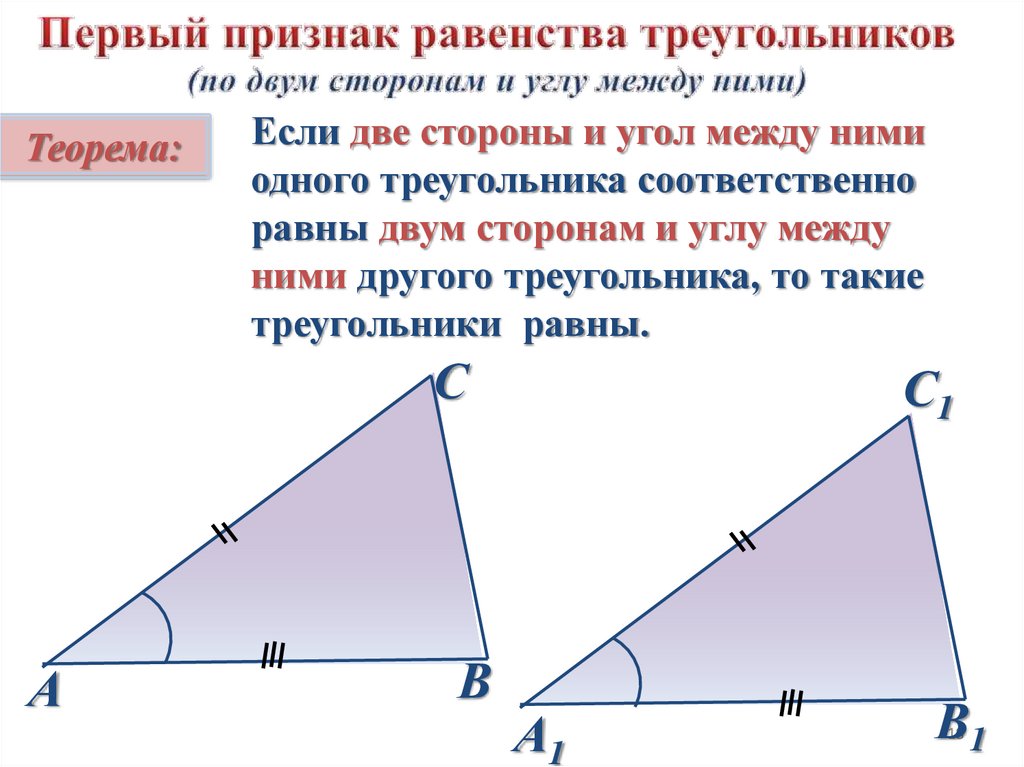
Теорема:
Если две стороны и угол между ними
одного треугольника соответственно
равны двум сторонам и углу между
ними другого треугольника, то такие
треугольники равны.
С
А
В
С1
А1
В1
18

19.

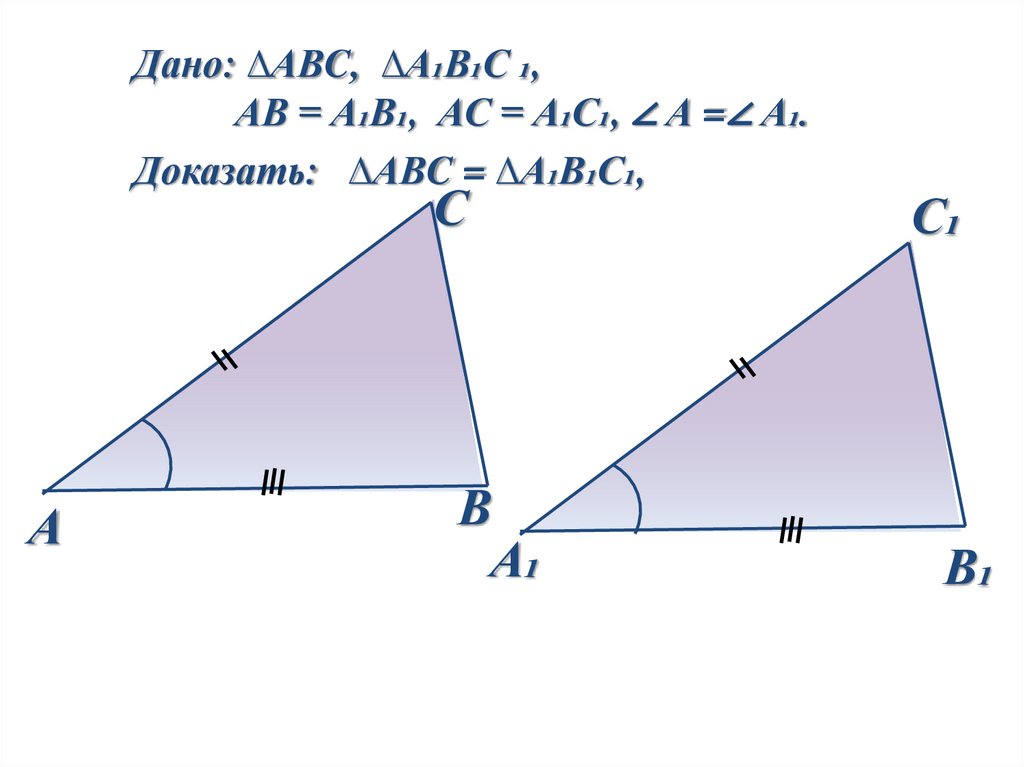
Дано: ∆АВC, ∆А₁В₁С ₁,
АВ = А₁В₁, АС = А₁С₁, ∠ А =∠ А₁.
Доказать: ∆АВC = ∆А₁В₁С₁,
А
С
С₁
В
А₁
В₁

20.

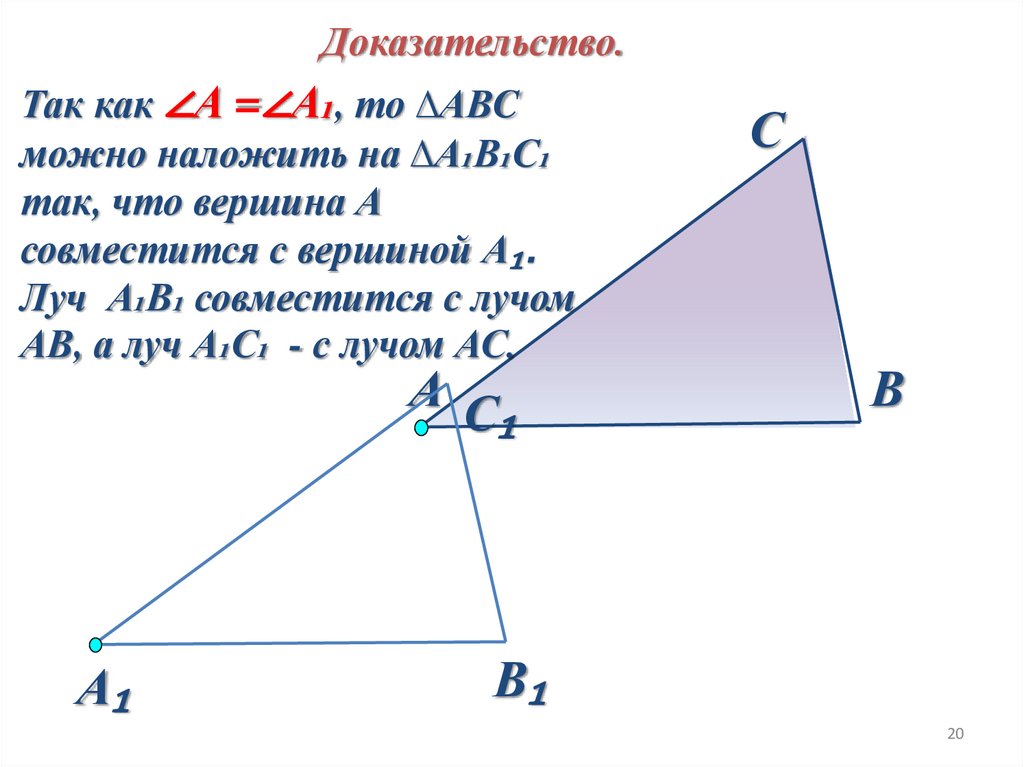
Доказательство.
Так как ∠А =∠А₁, то ∆АВC
можно наложить на ∆А₁В₁С₁
так, что вершина А
совместится с вершиной А₁.
Луч А₁В₁ совместится с лучом
АВ, а луч А₁С₁ - с лучом АС.
А С₁
А₁
С
В
В₁
20

21.

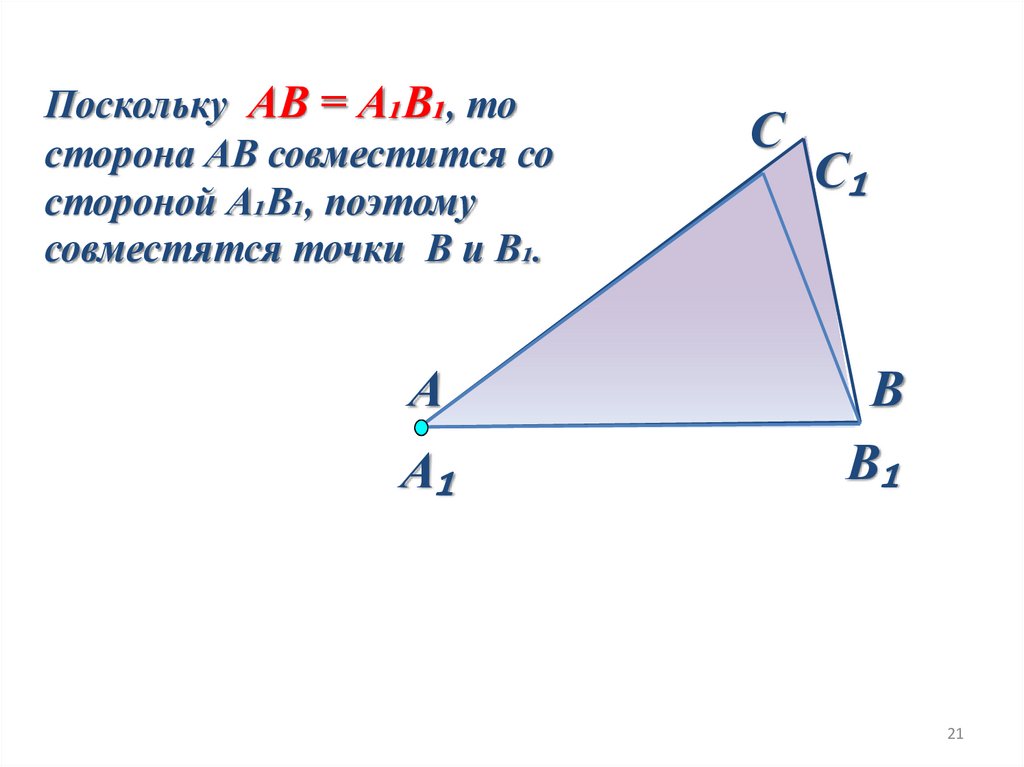
Поскольку АВ = А₁В₁, то
сторона АВ совместится со
стороной А₁В₁, поэтому
совместятся точки В и В₁.
А
А₁
С
С₁
В
В₁
21

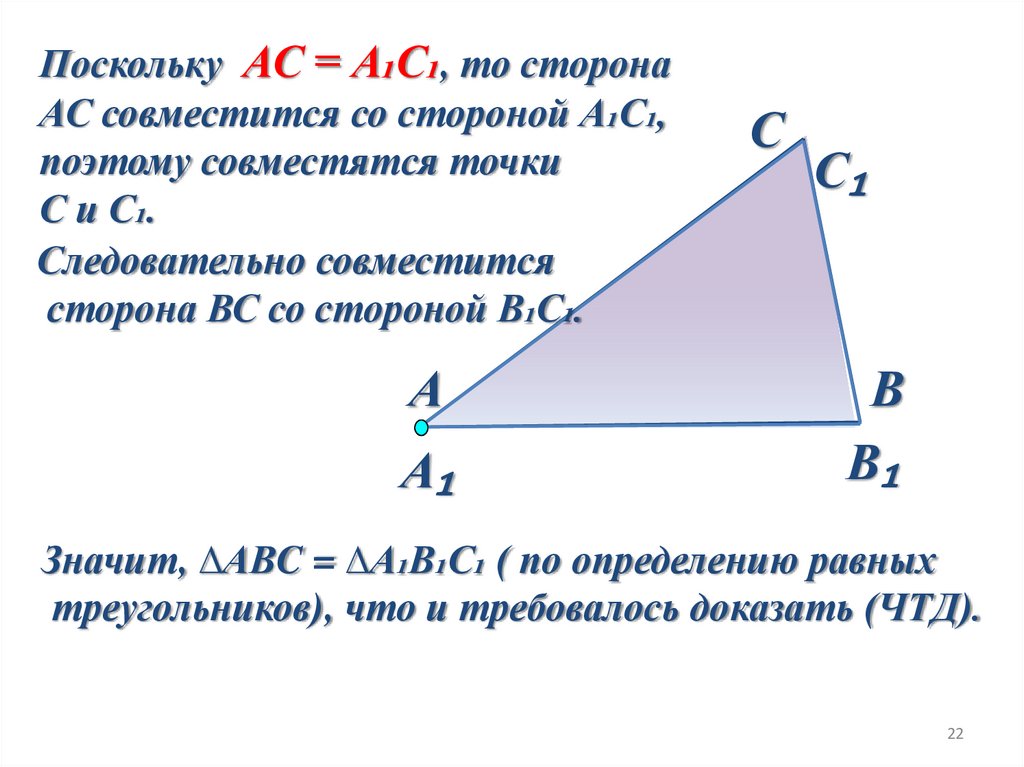
22.

Поскольку АС = А₁С₁, то сторона
АС совместится со стороной А₁С₁,
поэтому совместятся точки
С и С₁.
Следовательно совместится
сторона ВС со стороной В₁С₁.
А
А₁
С
С₁
В
В₁
Значит, ∆АВC = ∆А₁В₁С₁ ( по определению равных
треугольников), что и требовалось доказать (ЧТД).
22

23.

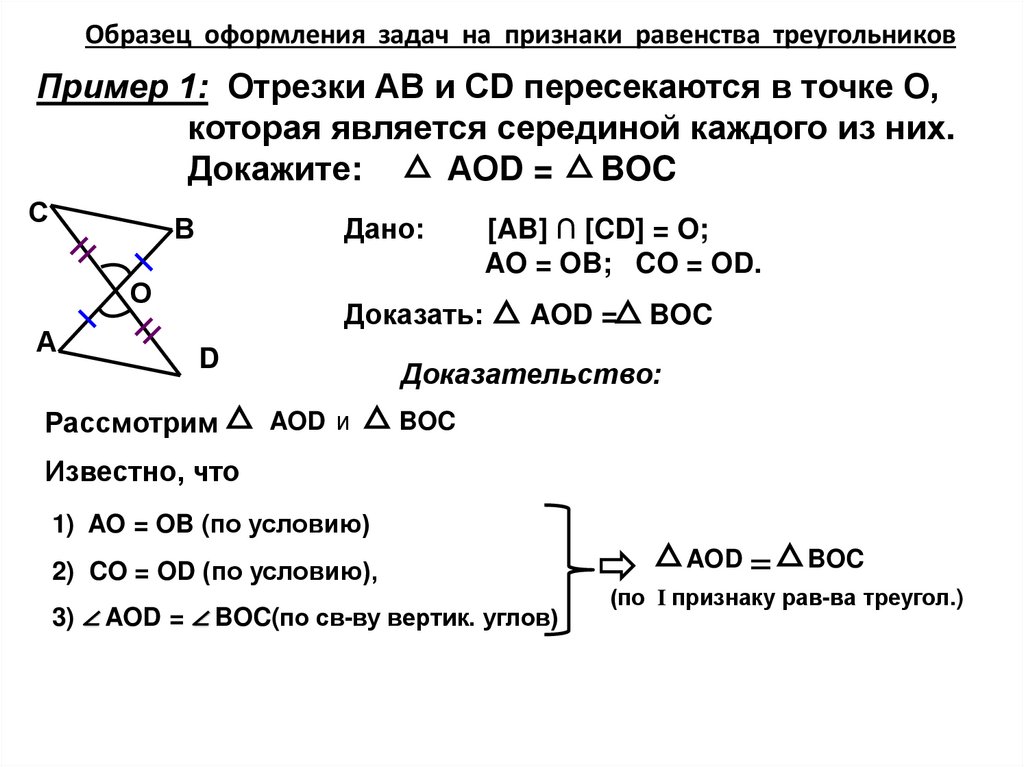
Образец оформления задач на признаки равенства треугольников
Пример 1: Отрезки АВ и СD пересекаются в точке О,
которая является серединой каждого из них.
Докажите:
АОD = BOC
С
В
Дано:
О
А
Доказать:
D
Рассмотрим
[AB] ∩ [CD] = O;
AO = OB; CO = OD.
AOD =
BOC
Доказательство:
AOD и
BOC
Известно, что
1) AO = OB (по условию)
2) CO = OD (по условию),
3) ∠ AOD = ∠ BOC(по св-ву вертик. углов)
AOD =
BOC
(по I признаку рав-ва треугол.)

24.

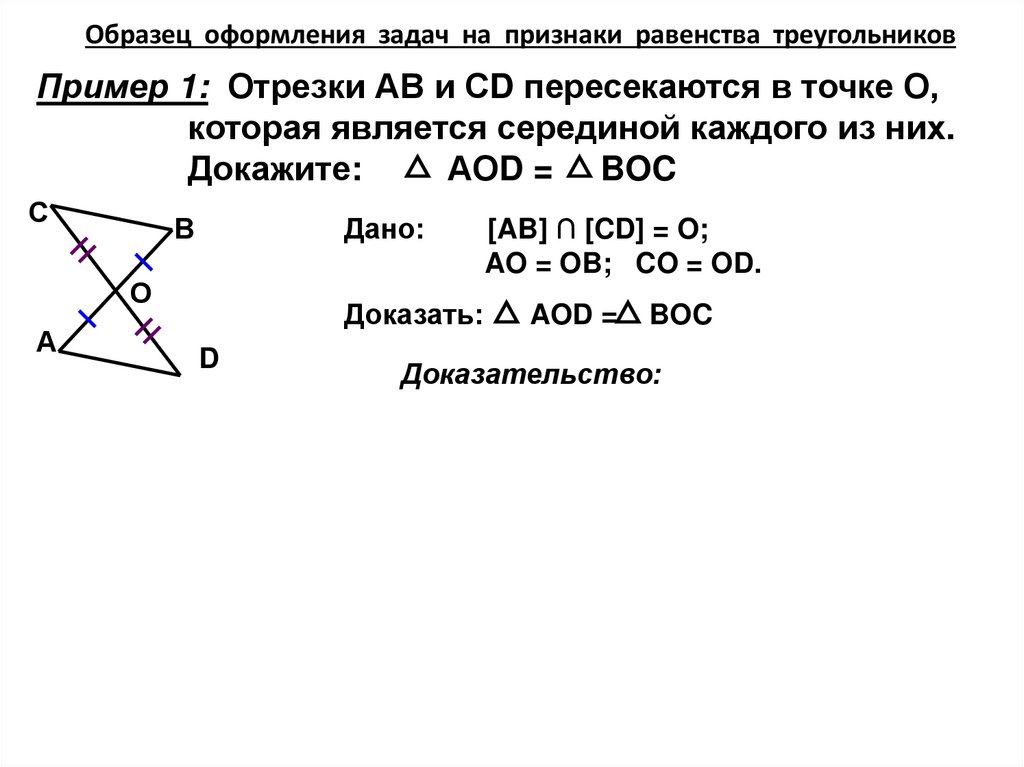
Образец оформления задач на признаки равенства треугольников
Пример 1: Отрезки АВ и СD пересекаются в точке О,
которая является серединой каждого из них.
Докажите:
АОD = BOC
С
В
Дано:
О
А
Доказать:
D
[AB] ∩ [CD] = O;
AO = OB; CO = OD.
AOD =
BOC
Доказательство:

25.

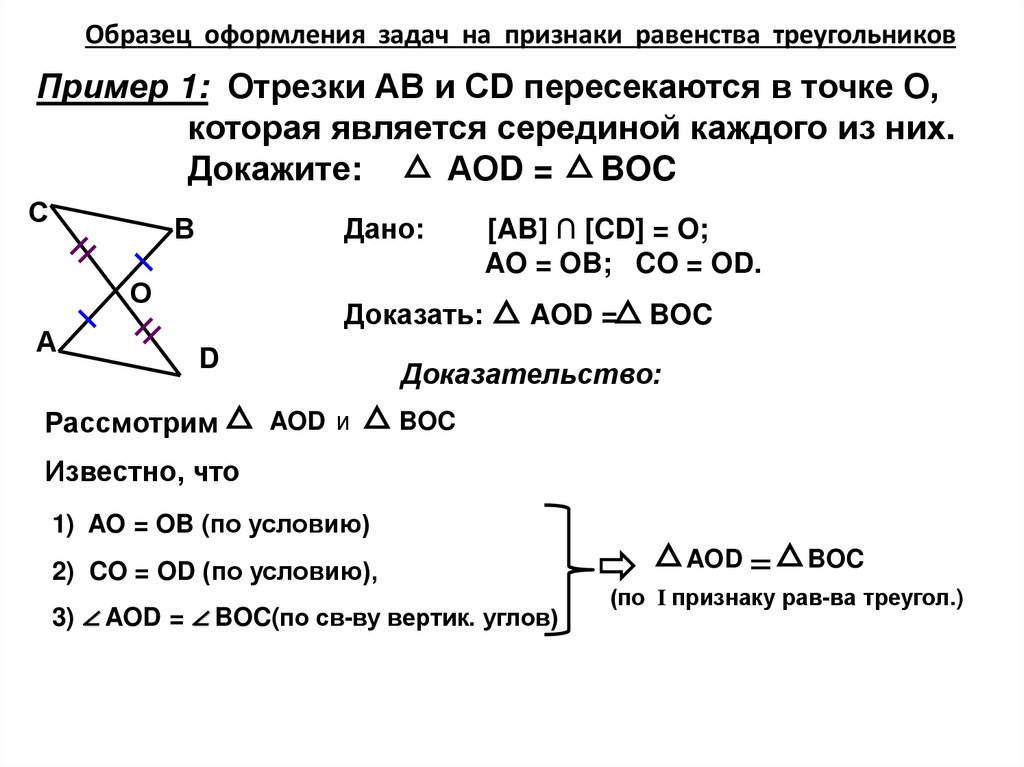
Образец оформления задач на признаки равенства треугольников
Пример 1: Отрезки АВ и СD пересекаются в точке О,
которая является серединой каждого из них.
Докажите:
АОD = BOC
С
В
Дано:
О
А
Доказать:
D
Рассмотрим
[AB] ∩ [CD] = O;
AO = OB; CO = OD.
AOD =
BOC
Доказательство:
AOD и
BOC
Известно, что
1) AO = OB (по условию)
2) CO = OD (по условию),
3) ∠ AOD = ∠ BOC(по св-ву вертик. углов)
AOD =
BOC
(по I признаку рав-ва треугол.)

26.

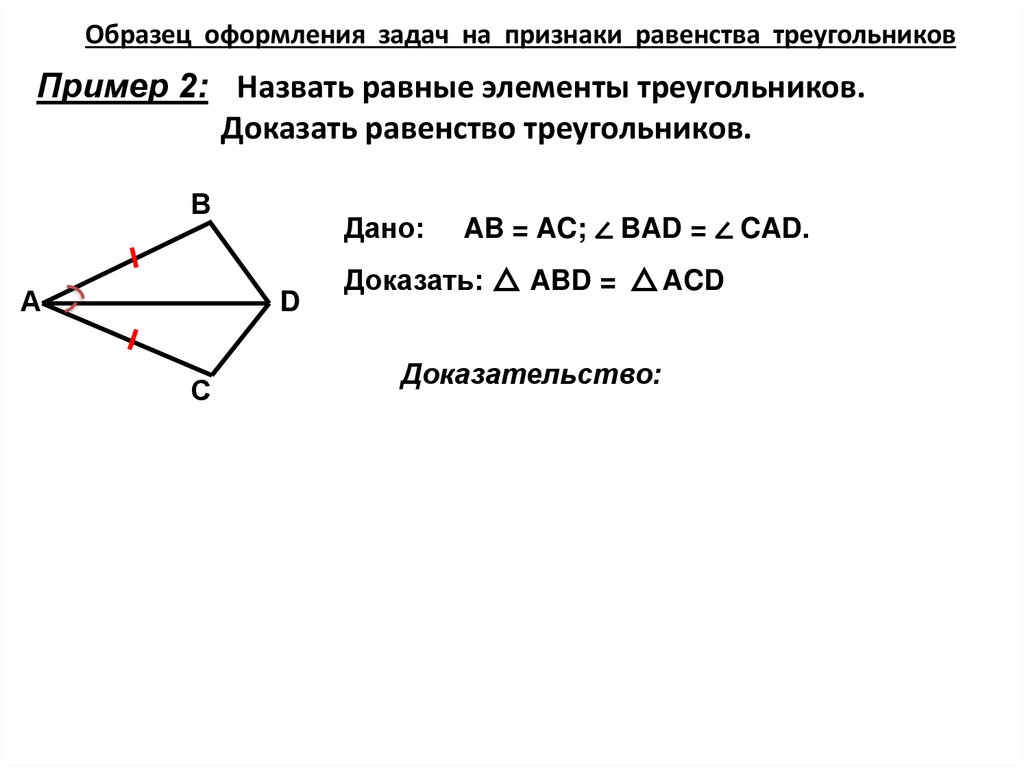
Образец оформления задач на признаки равенства треугольников
Пример 2: Назвать равные элементы треугольников.
Доказать равенство треугольников.
В
А
Дано:
D
С
AB = AC; ∠ BAD = ∠ CAD.
Доказать:
ABD =
Доказательство:
ACD

27.

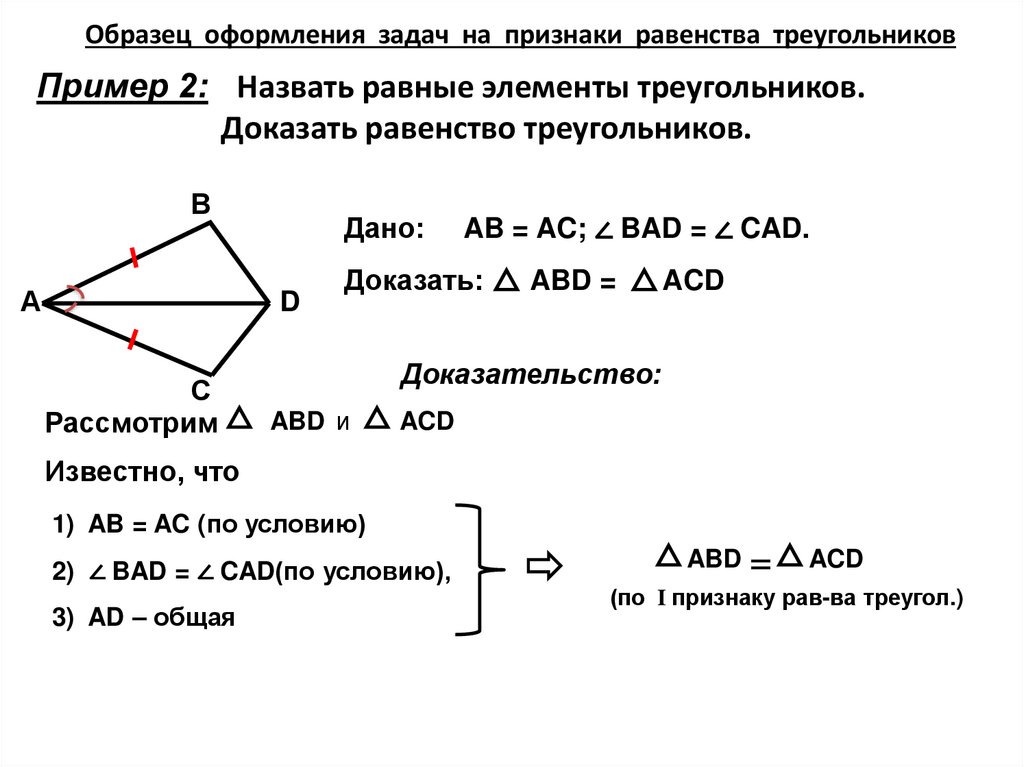
Образец оформления задач на признаки равенства треугольников
Пример 2: Назвать равные элементы треугольников.
Доказать равенство треугольников.
В
А
Дано:
D
С
Рассмотрим
AB = AC; ∠ BAD = ∠ CAD.
Доказать:
ABD =
ACD
Доказательство:
ABD и
ACD
Известно, что
1) AB = AC (по условию)
2) ∠ BAD = ∠ CAD(по условию),
3) AD – общая
ABD =
ACD
(по I признаку рав-ва треугол.)

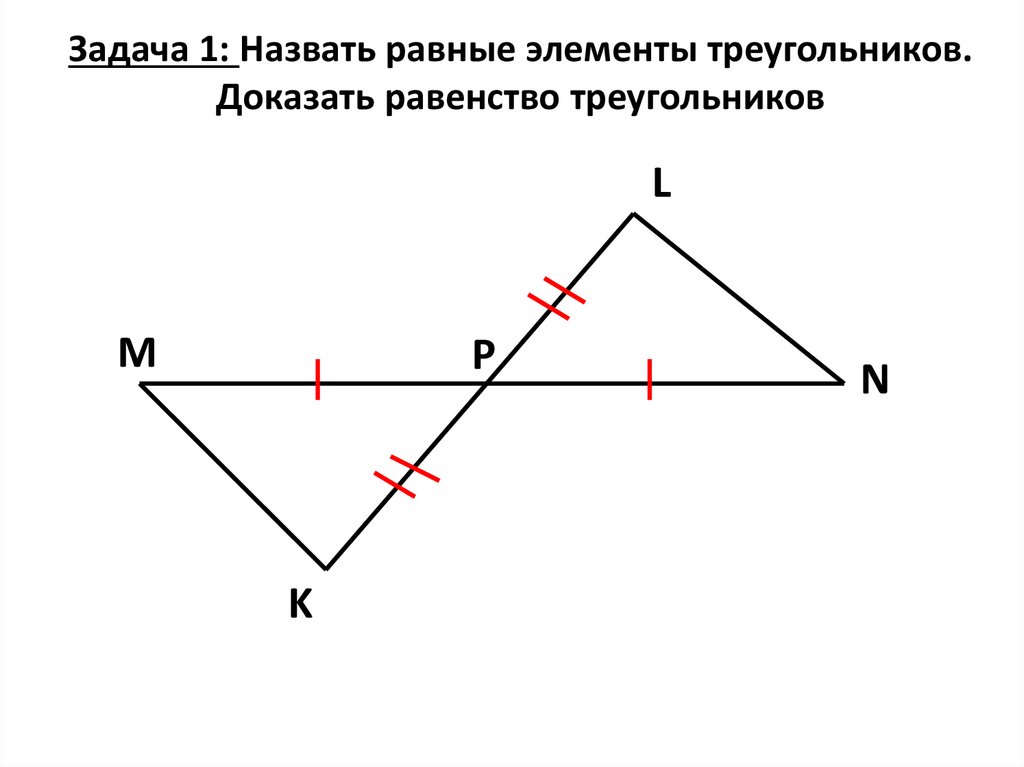
28. Задача 1: Назвать равные элементы треугольников. Доказать равенство треугольников

L
M
P
K
N

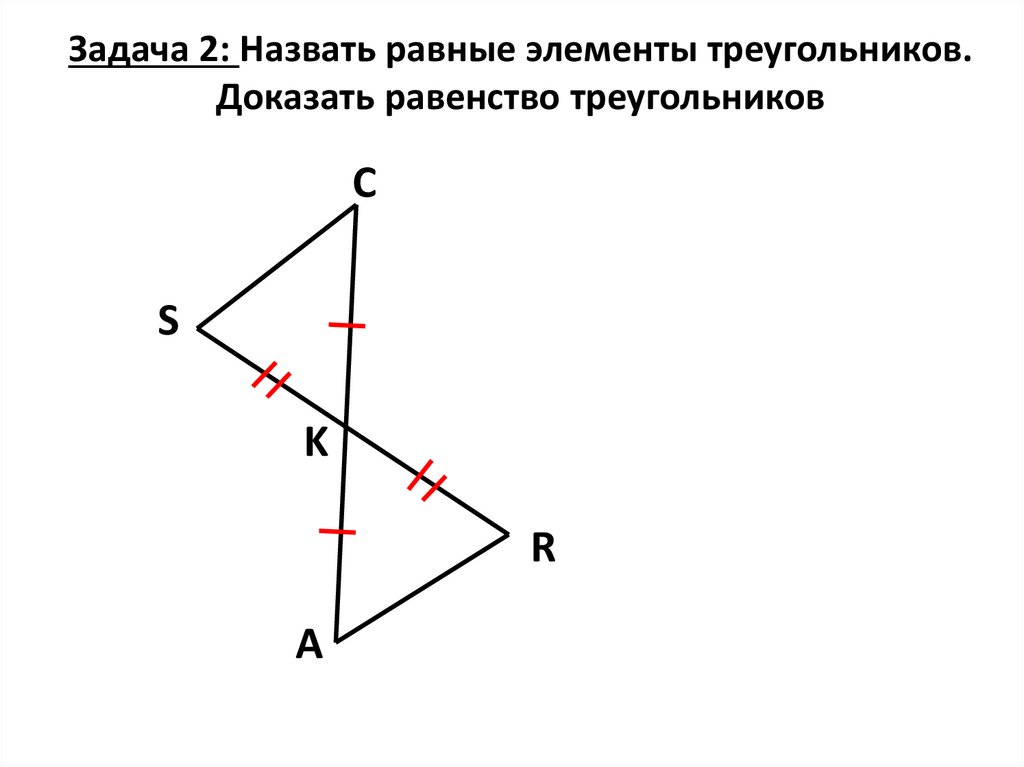
29. Задача 2: Назвать равные элементы треугольников. Доказать равенство треугольников

C
S
K
R
A

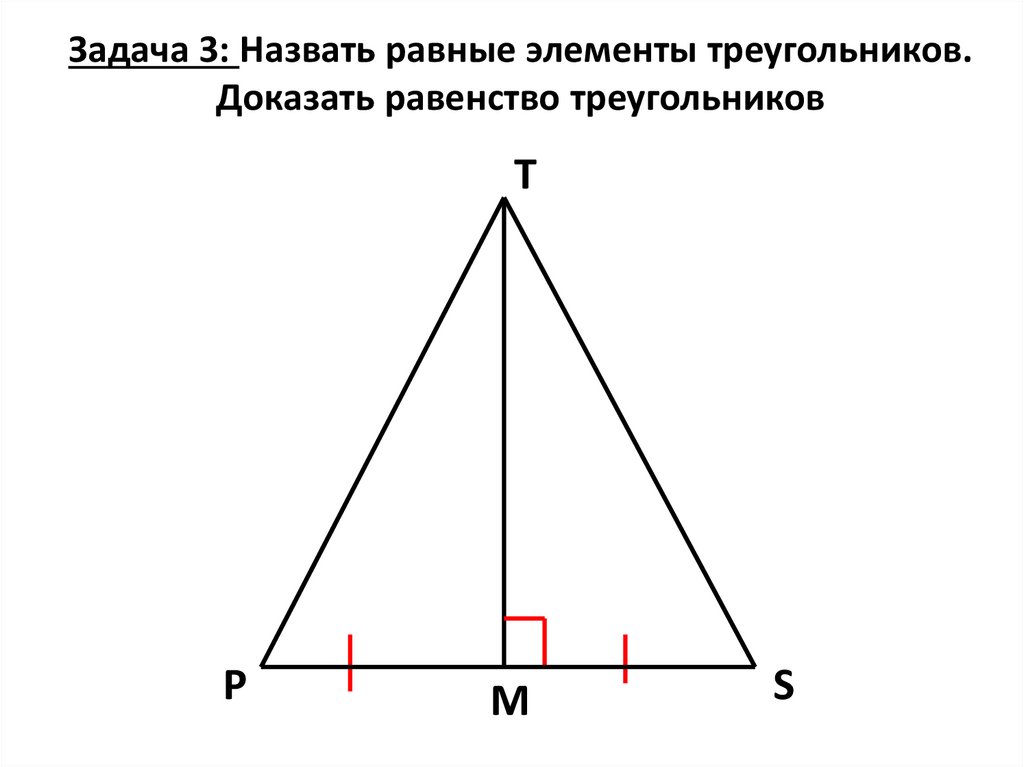
30.

Задача 3: Назвать равные элементы треугольников.
Доказать равенство треугольников
T
P
M
S

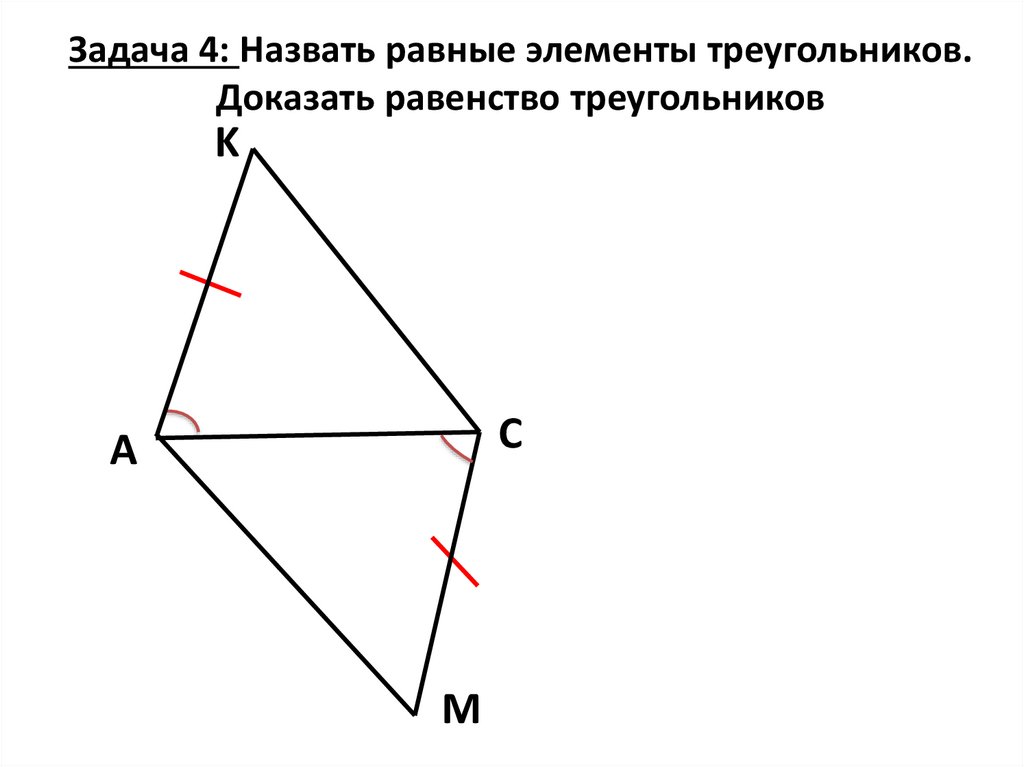
31.

Задача 4: Назвать равные элементы треугольников.
Доказать равенство треугольников
K
С
A
M

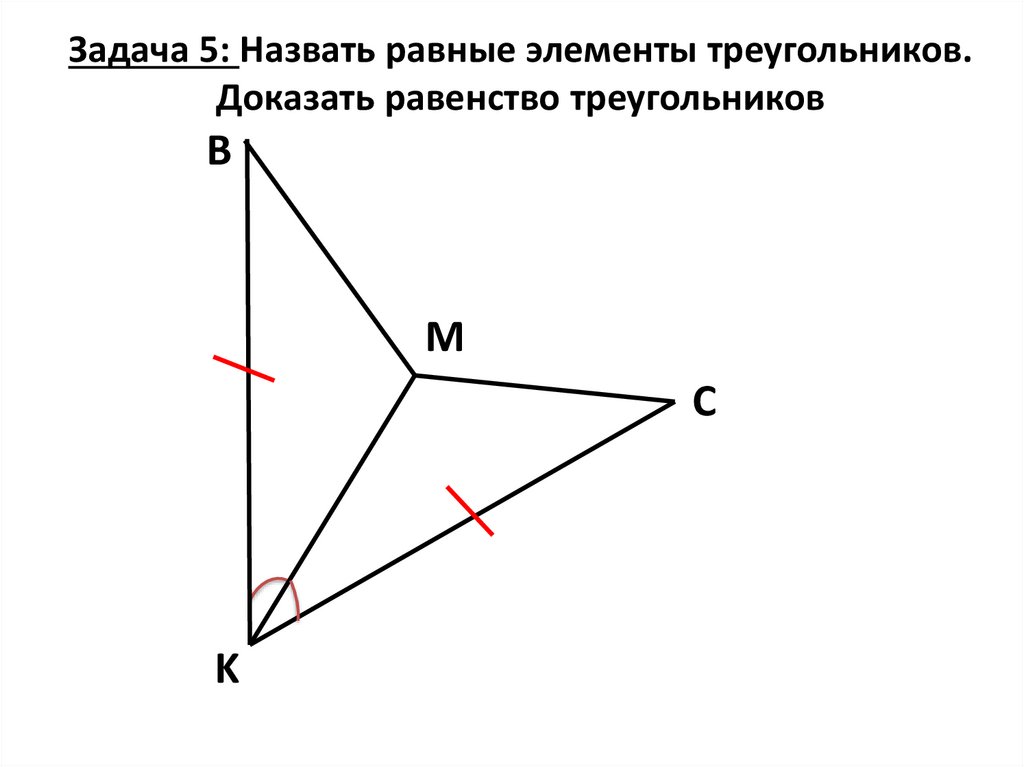
32.

Задача 5: Назвать равные элементы треугольников.
Доказать равенство треугольников
В
M
С
K

33.

Что такое теорема и доказательство теоремы?
Сформулировать первый признак равенства
треугольников.
Доказать теорему, выражающую первый признак
равенства треугольников.
34

34.

С. 28-30, I призн.равен.треуг.
(доказывать!!!)
Упр. 94, 95, 96.
35