Презентация по геометрии 10 класс _Построение сечений тетраэдра и параллелепипеда_

1.

Уроки геометрии в 10 классе

2.

Цель уроков:
Сформировать умения у учащихся строить сечения
тетраэдра и параллелепипеда заданной плоскостью.
Задачи:
Дать определение секущей плоскости и определение сечения
многогранника.
Познакомить с правилами построения сечений тетраэдра и
параллелепипеда.
Рассмотреть возможные варианты сечений тетраэдра и параллелепипеда.
Выработать навыки построения сечений тетраэдра и параллелепипеда при
различных случаях задания секущей плоскости.
Способствовать формированию у учащихся пространственного
воображения.
Развивать умения у учащихся анализировать, сравнивать, обобщать, делать
выводы.
Способствовать развитию умения пользоваться чертежными
инструментами и умению выполнять построения более четко, наглядно и
аккуратно.

3.

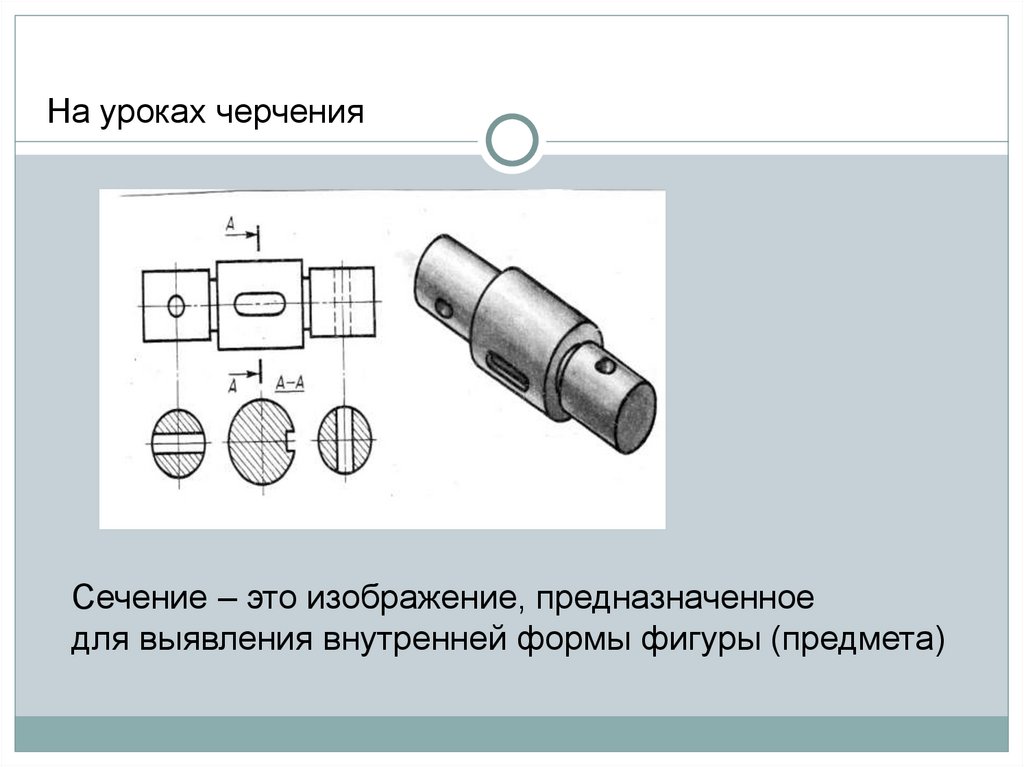
На уроках черчения
Сечение – это изображение, предназначенное
для выявления внутренней формы фигуры (предмета)

4.

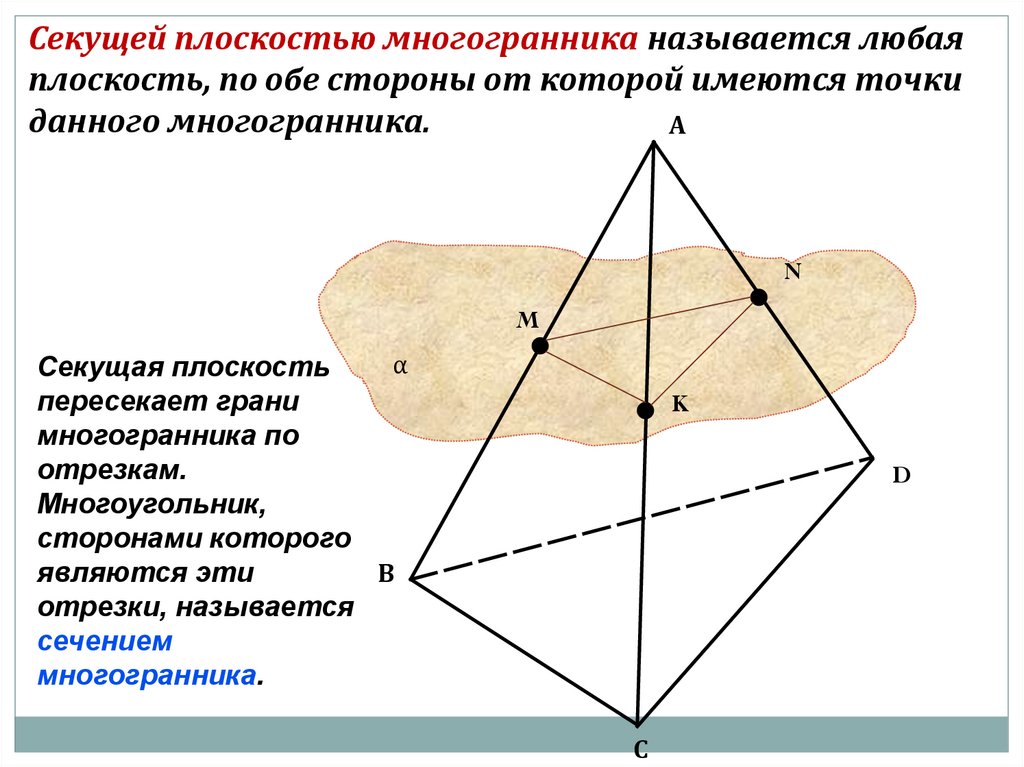
Секущей плоскостью многогранника называется любая
плоскость, по обе стороны от которой имеются точки
данного многогранника.
А
N
M
α
Секущая плоскость
пересекает грани
многогранника по
отрезкам.
Многоугольник,
сторонами которого
являются эти
В
отрезки, называется
сечением
многогранника.
K
D
С

5.

Аксиомы и теоремы стереометрии
В
А
α
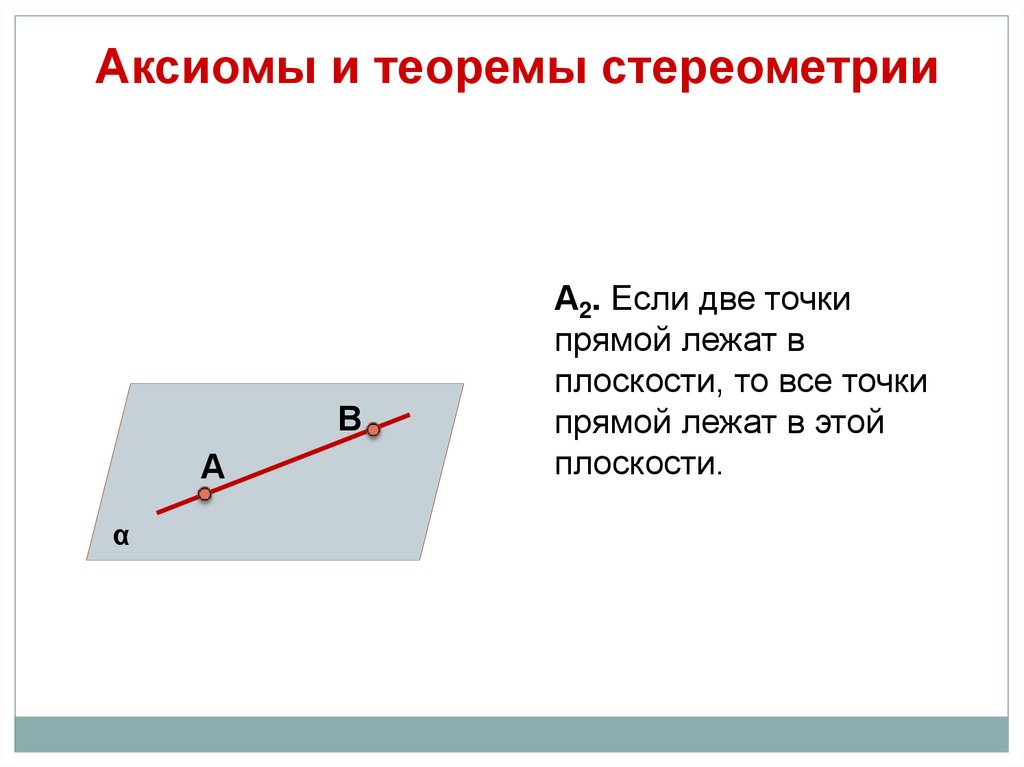
А2. Если две точки
прямой лежат в
плоскости, то все точки
прямой лежат в этой
плоскости.

6.

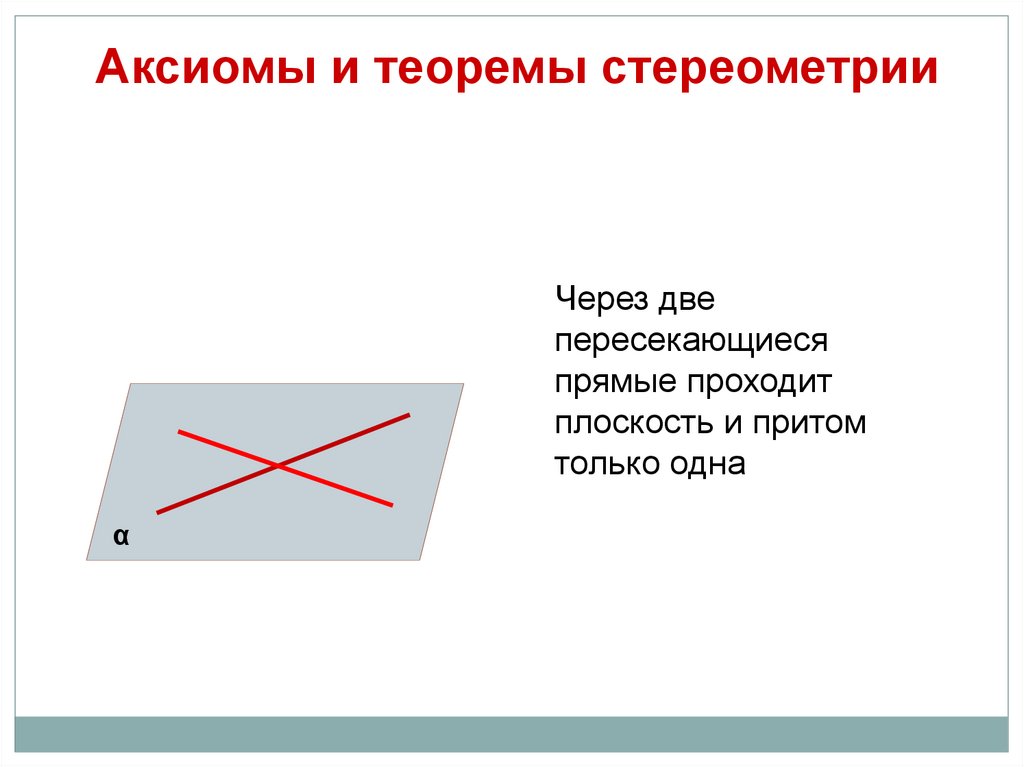
Аксиомы и теоремы стереометрии
Через две
пересекающиеся
прямые проходит
плоскость и притом
только одна
α

7.

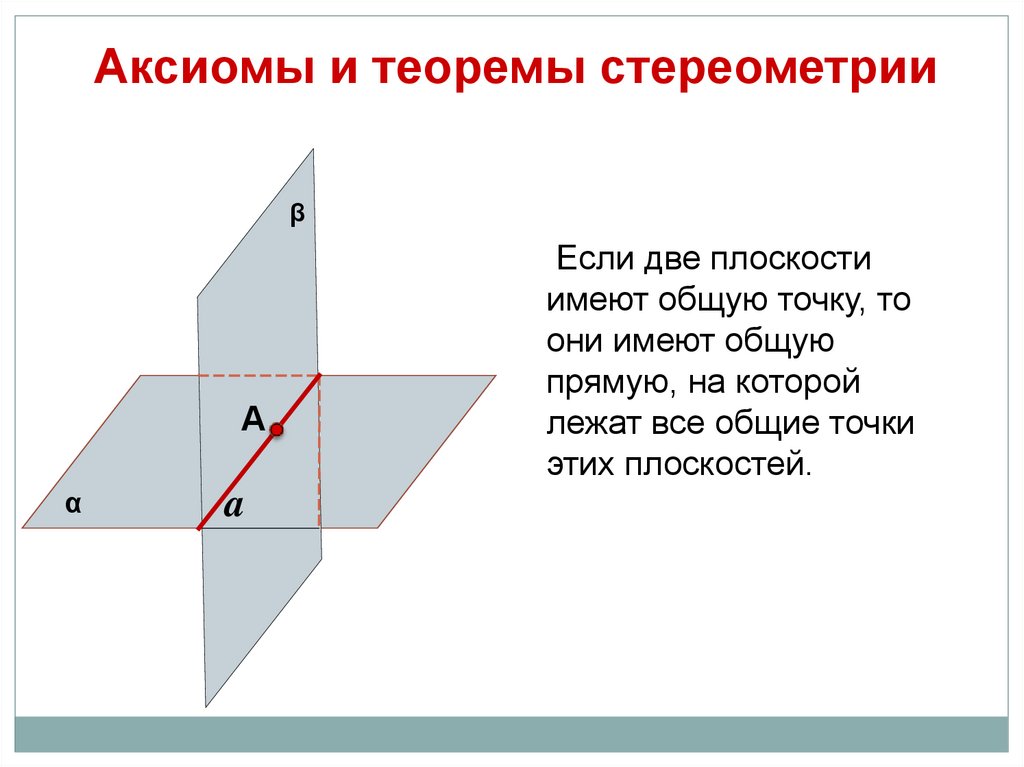
Аксиомы и теоремы стереометрии
β
А
α
a
Если две плоскости
имеют общую точку, то
они имеют общую
прямую, на которой
лежат все общие точки
этих плоскостей.

8.

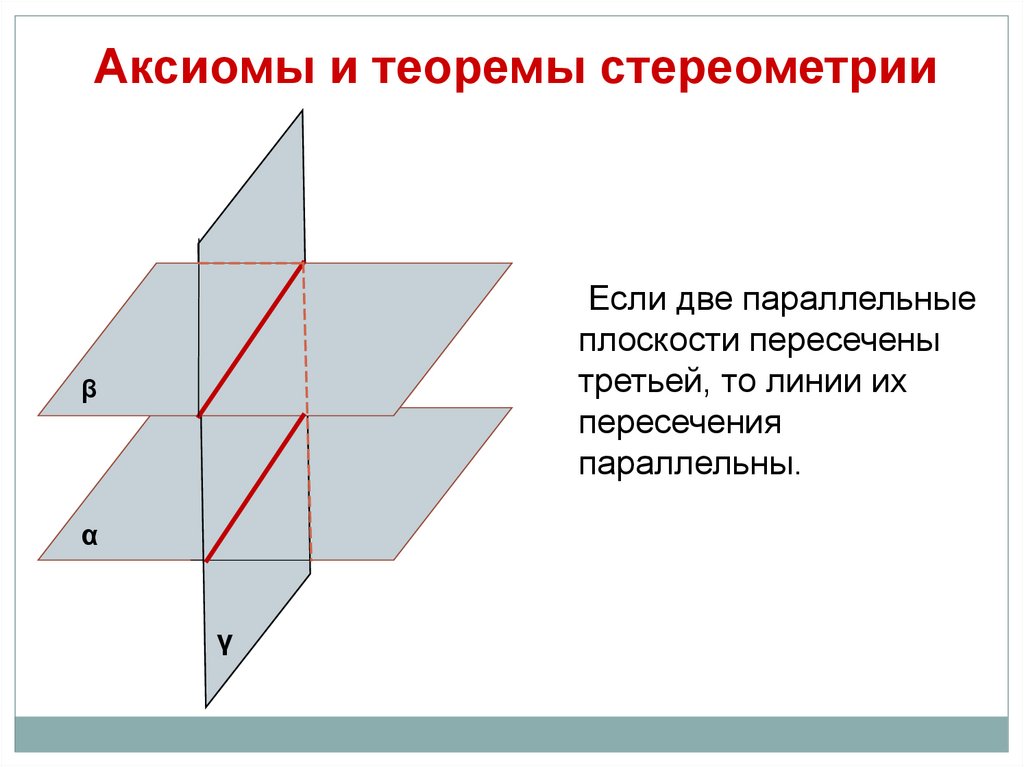
Аксиомы и теоремы стереометрии
Если две параллельные
плоскости пересечены
третьей, то линии их
пересечения
параллельны.
β
α
γ

9.

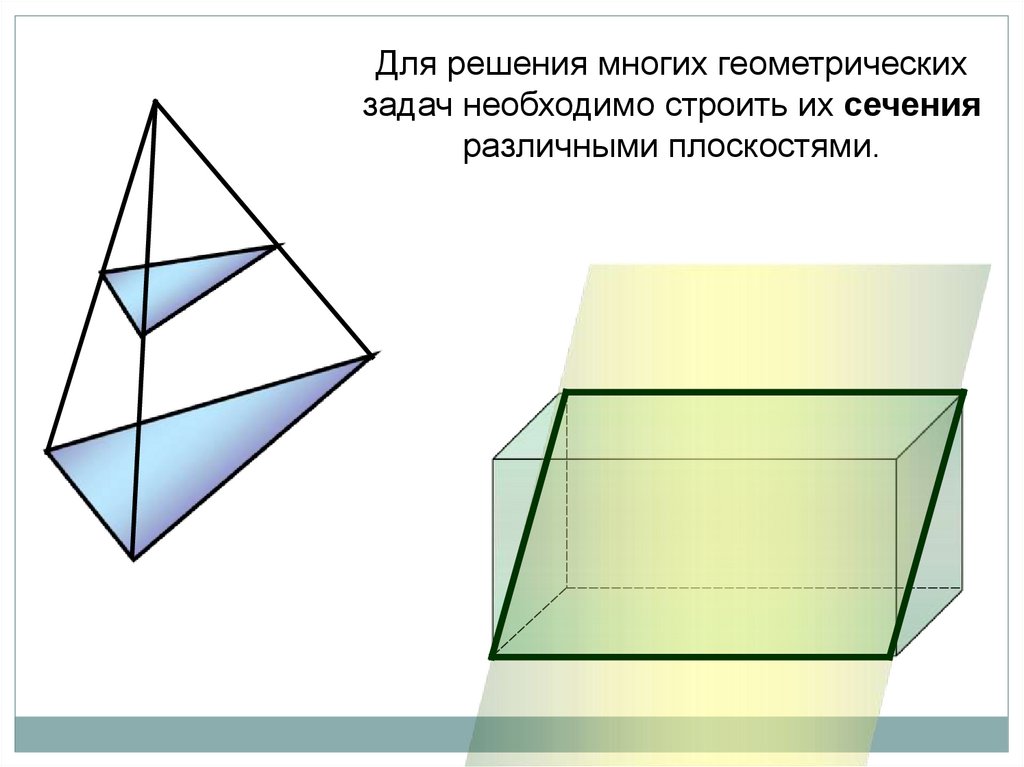
Для решения многих геометрических
задач необходимо строить их сечения
различными плоскостями.

10.

Для построения сечения нужно построить
точки пересечения секущей плоскости с
ребрами и соединить их отрезками.
1. Соединять можно только две точки, лежащие в
плоскости одной грани.
2. Секущая плоскость пересекает
грани по параллельным отрезкам.
параллельные
3. Если в плоскости грани отмечена только одна точка,
принадлежащая плоскости сечения, то надо построить
дополнительную точку. Для этого необходимо найти
точки пересечения уже построенных прямых с другими
прямыми, лежащими в тех же гранях.

11.

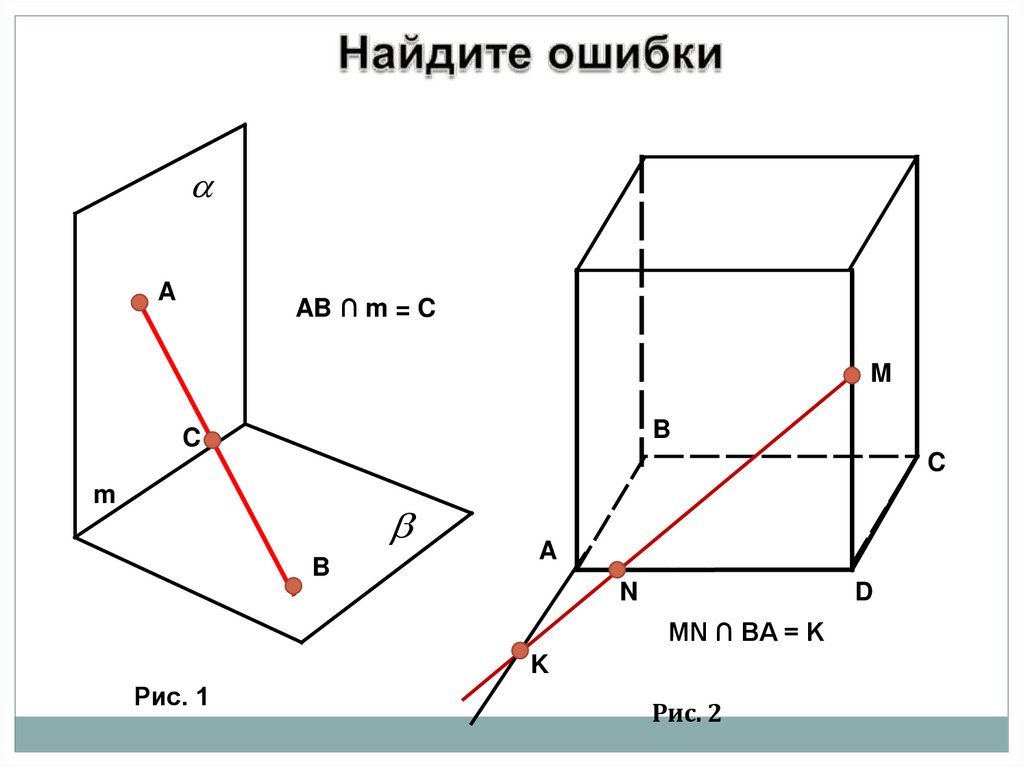
A
AB ∩ m = C
M
B
C
C
m
B
A
N
D
MN ∩ BA = K
K
Рис. 1
Рис. 2

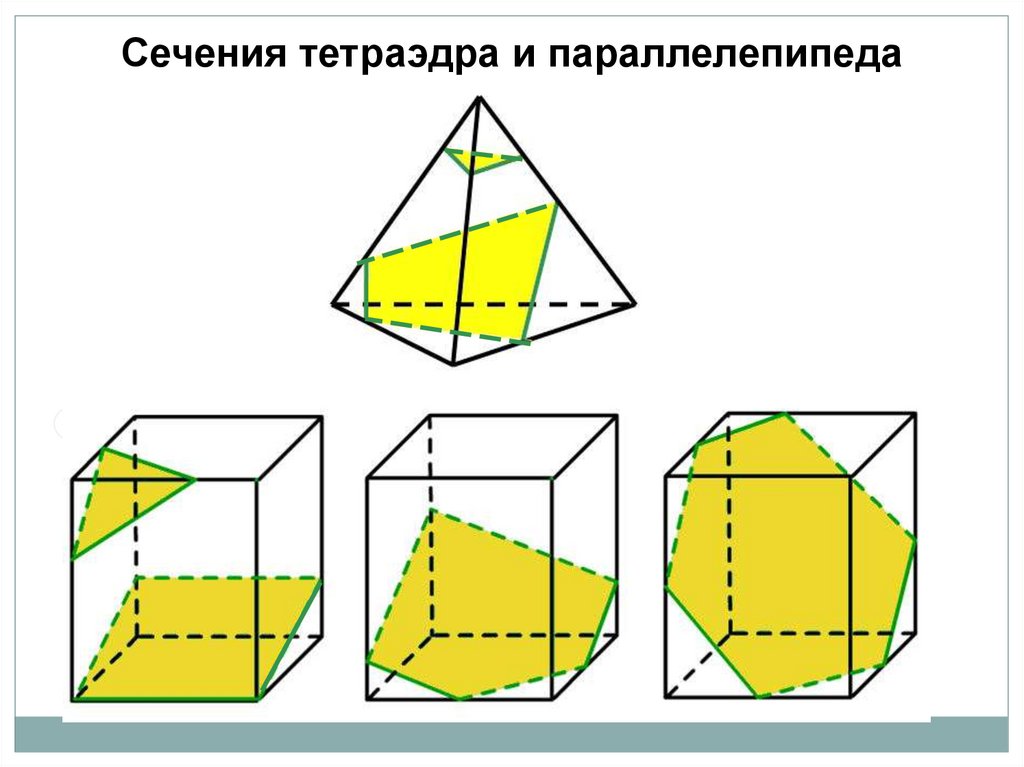
12.

Сечения тетраэдра и параллелепипеда

13.

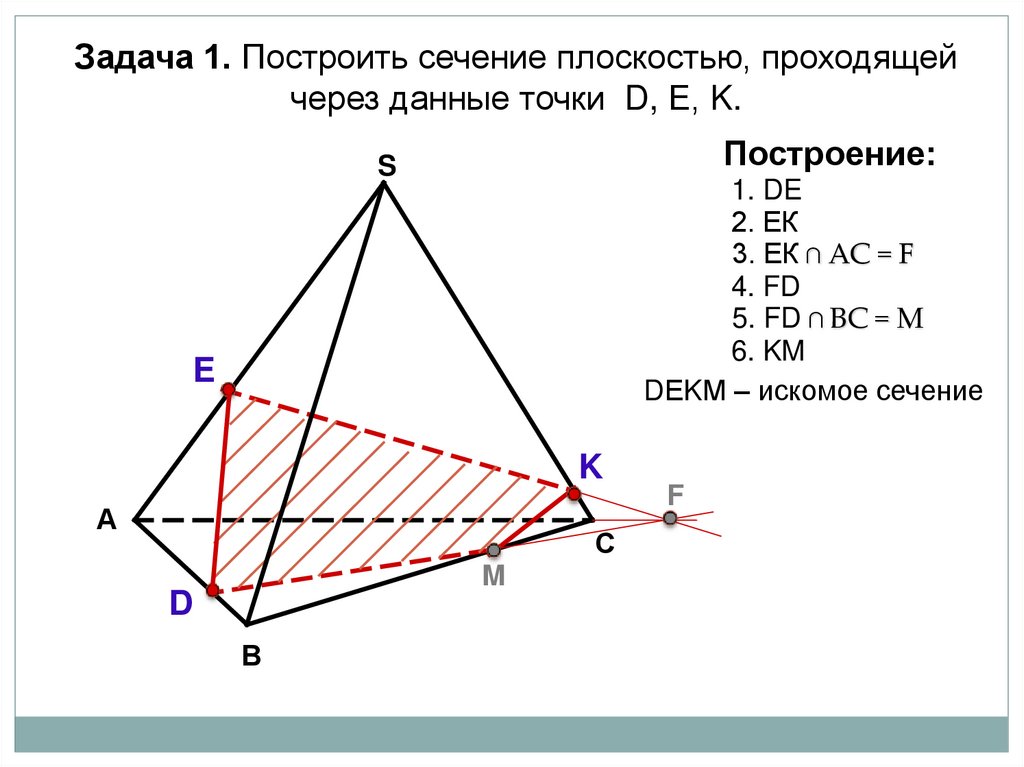
Задача 1. Построить сечение плоскостью, проходящей
через данные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F

14.

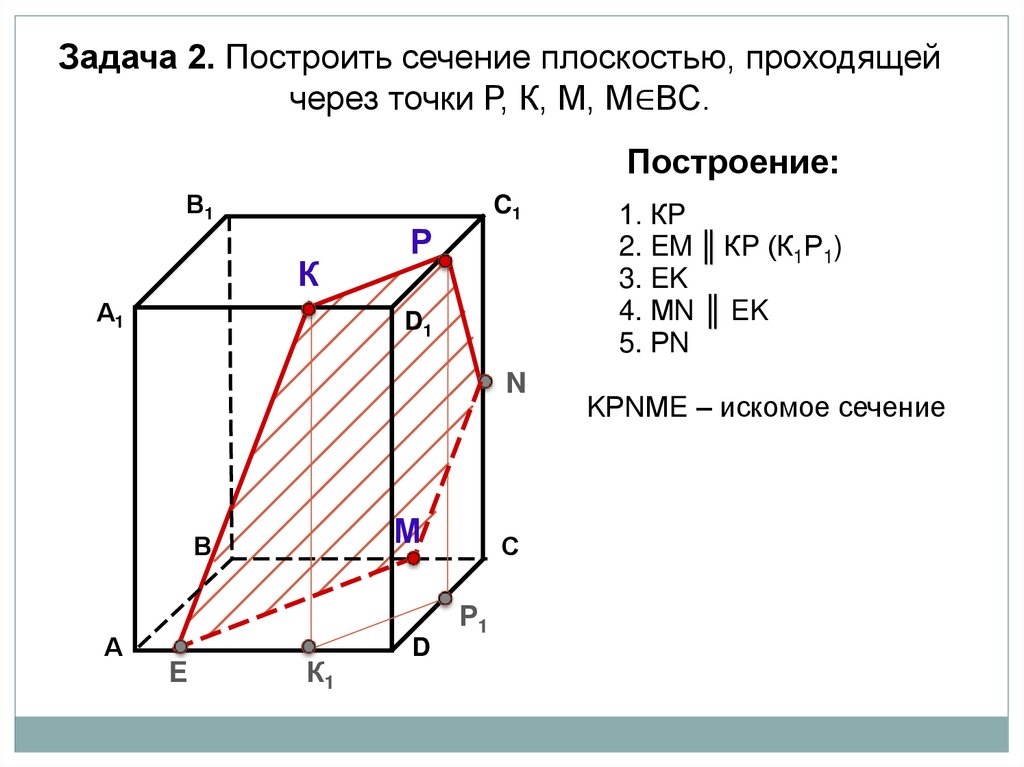
Задача 2. Построить сечение плоскостью, проходящей
через точки Р, К, М, М∈ВС.
Построение:
В1
К
А1
C1
Р
D1
N
М
В
А
С
Р1
E
К1
D
1. КP
2. EM ║ КP (К1Р1)
3. EK
4. МN ║ EK
5. РN
KРNМE – искомое сечение

15.

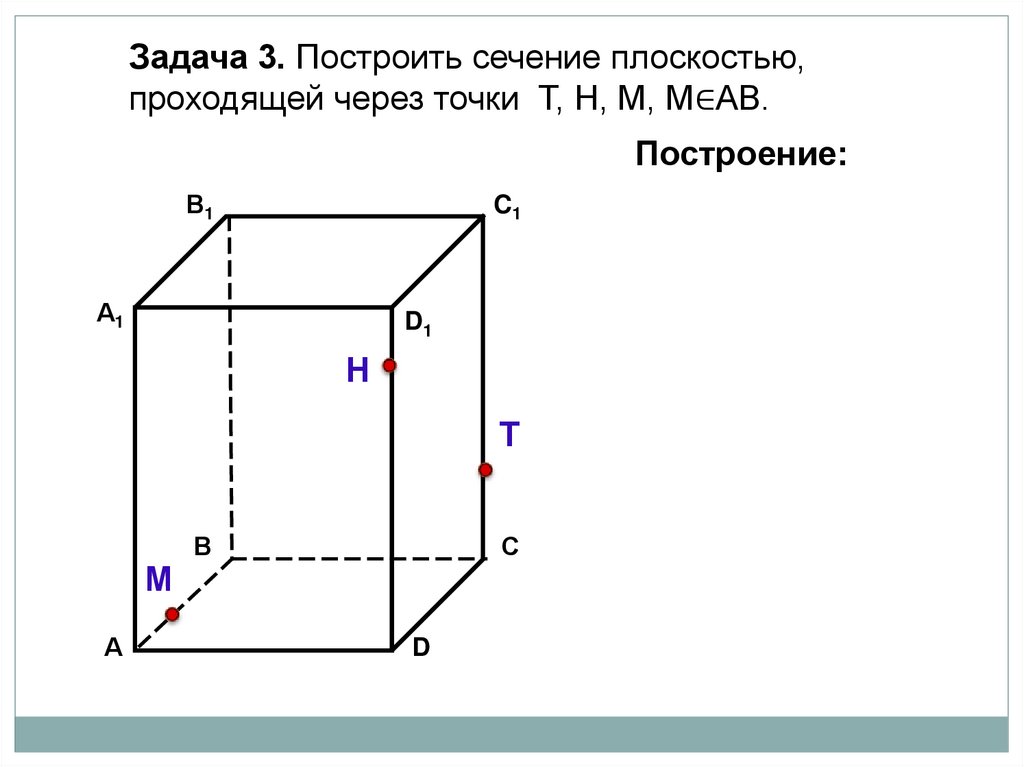
Задача 3. Построить сечение плоскостью,
проходящей через точки Т, Н, М, М∈АВ.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D

16.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
C1
А1
D1
Н
Т
М
А
В
С
D
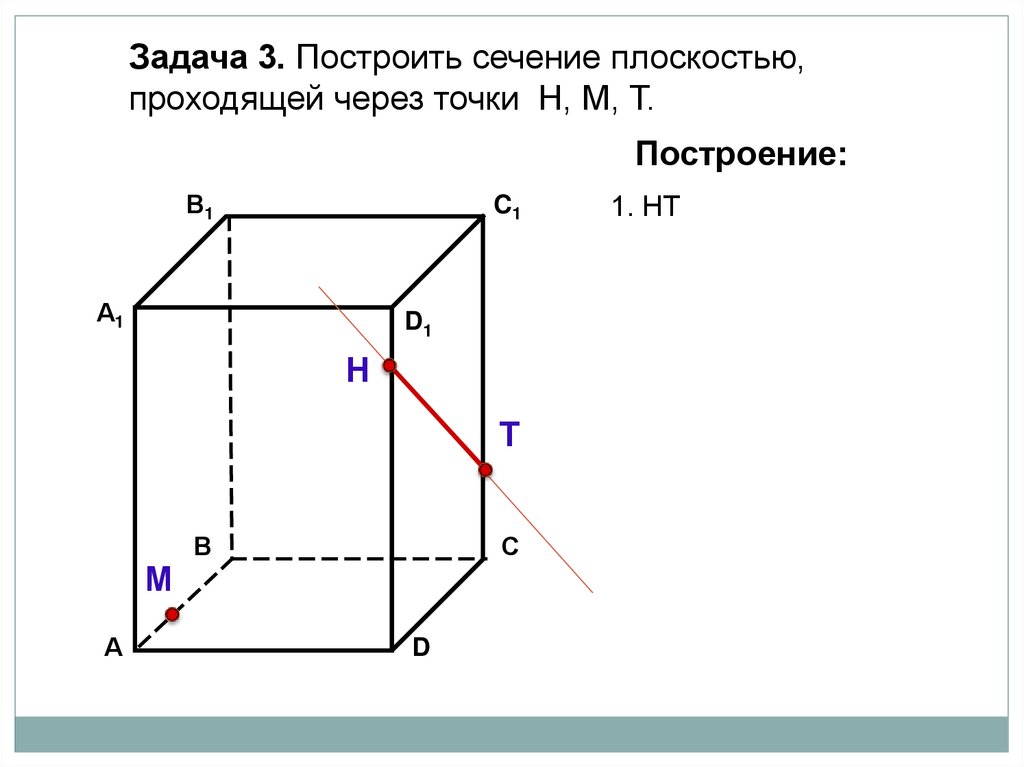
1. НТ

17.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
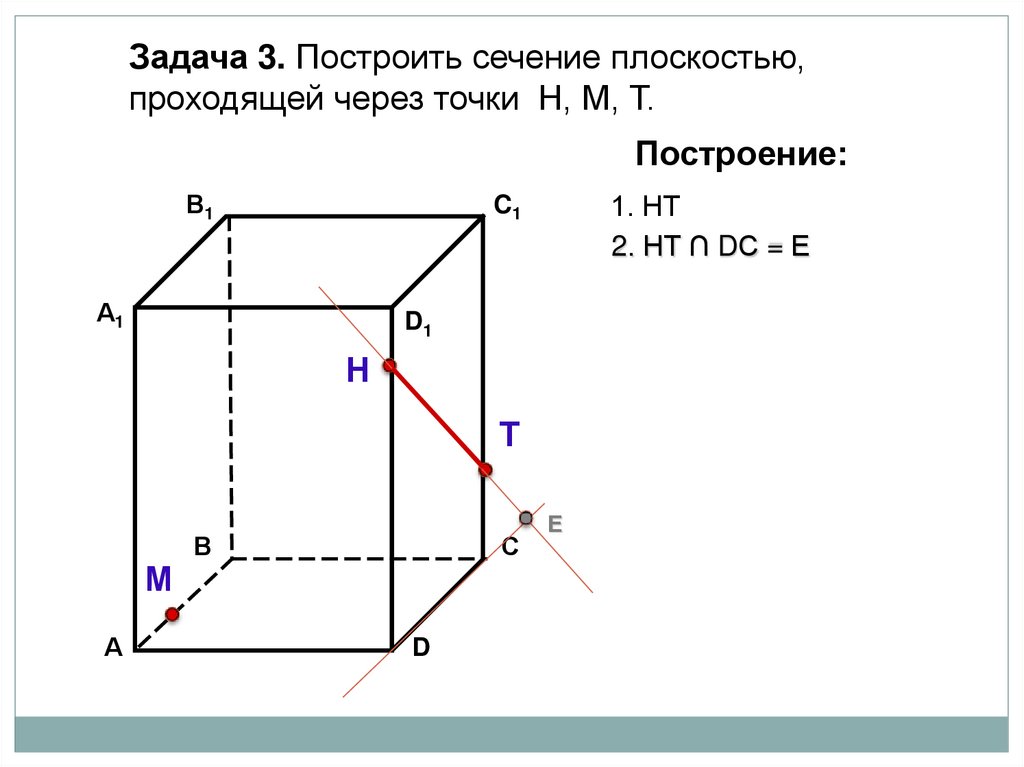
1. НТ
2. НТ ∩ DС = Е
C1
А1
D1
Н
Т
М
А
В
С
D
Е

18.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
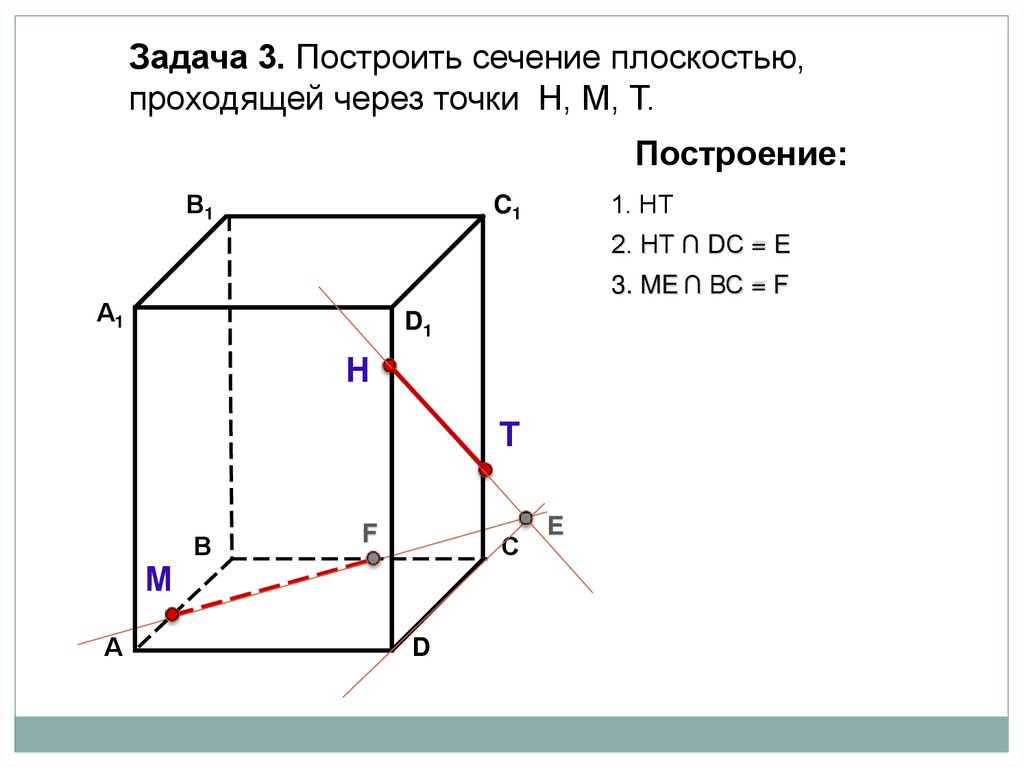
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
D1
Н
Т
М
А
В
F
С
D
E

19.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
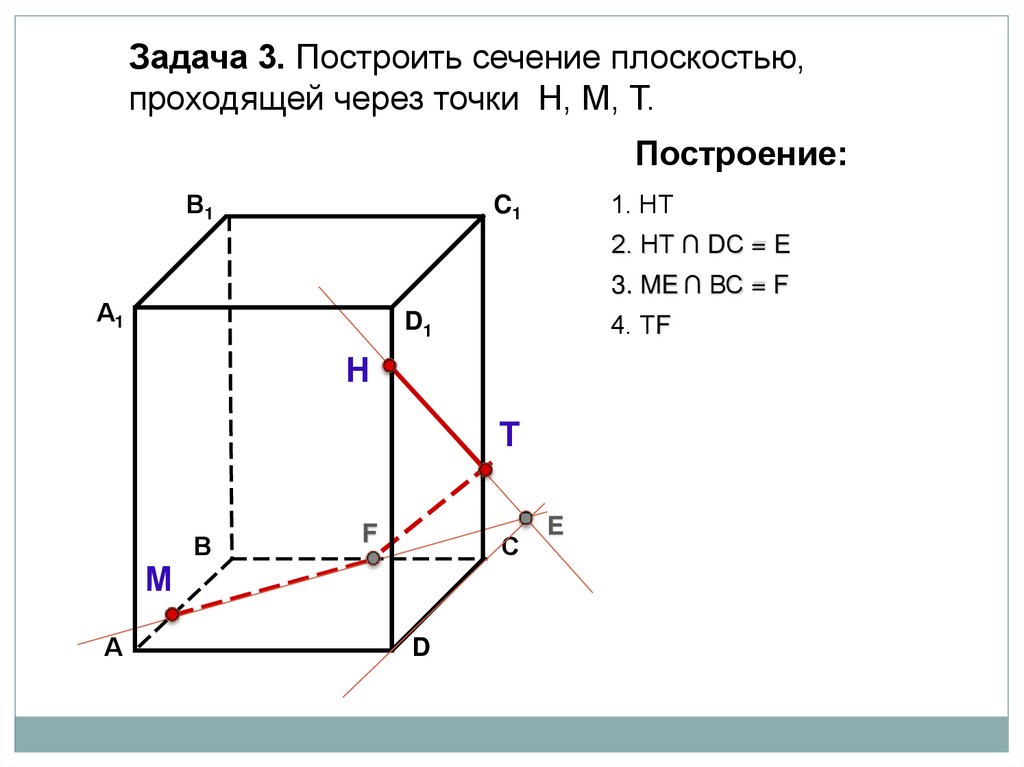
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
Н
Т
М
А
В
F
С
D
E

20.

Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
Т
М
F
В
А
С
D
K
E

21.

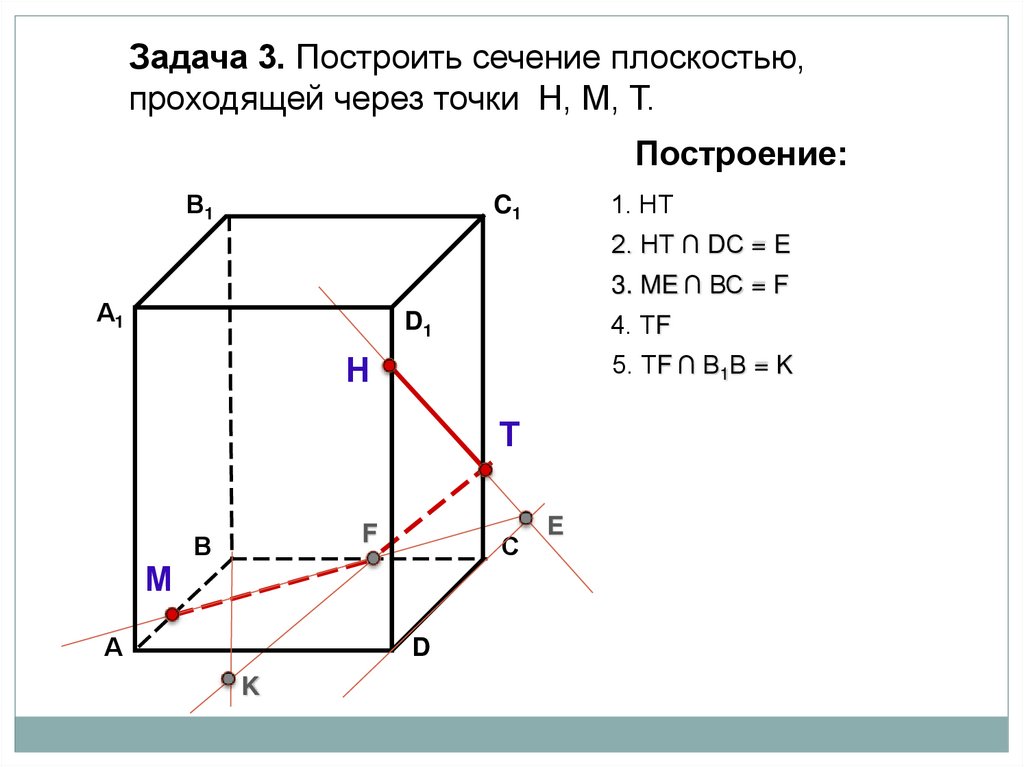
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
М
L
F
В
А
С
D
K
E

22.

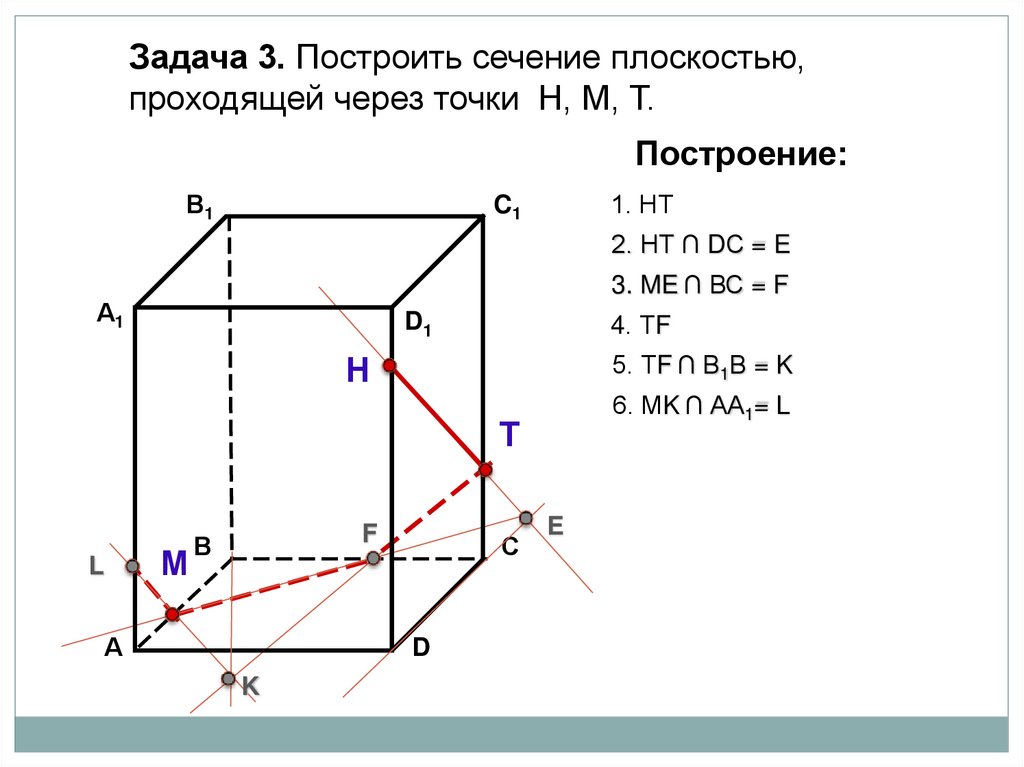
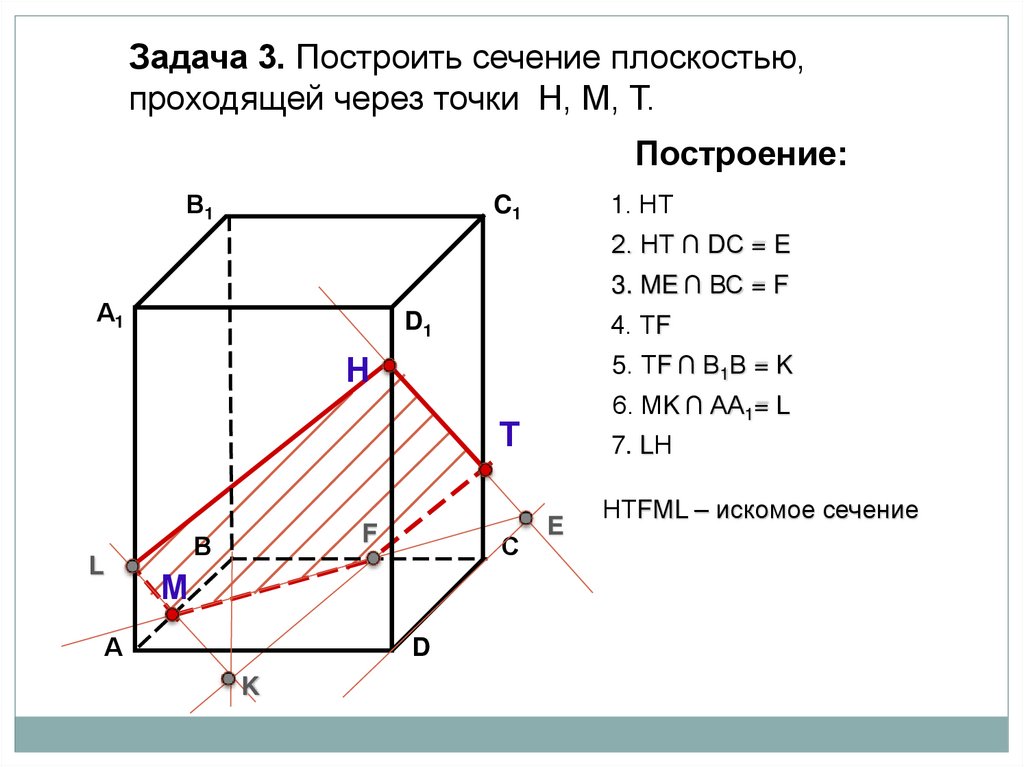
Задача 3. Построить сечение плоскостью,
проходящей через точки Н, М, Т.
Построение:
В1
1. НТ
C1
2. НТ ∩ DС = E
3. ME ∩ ВС = F
А1
4. ТF
D1
5. ТF ∩ В1В = K
Н
6. МK ∩ АА1= L
Т
F
В
L
С
М
А
D
K
7. LН
E
НТFМL – искомое сечение

23.

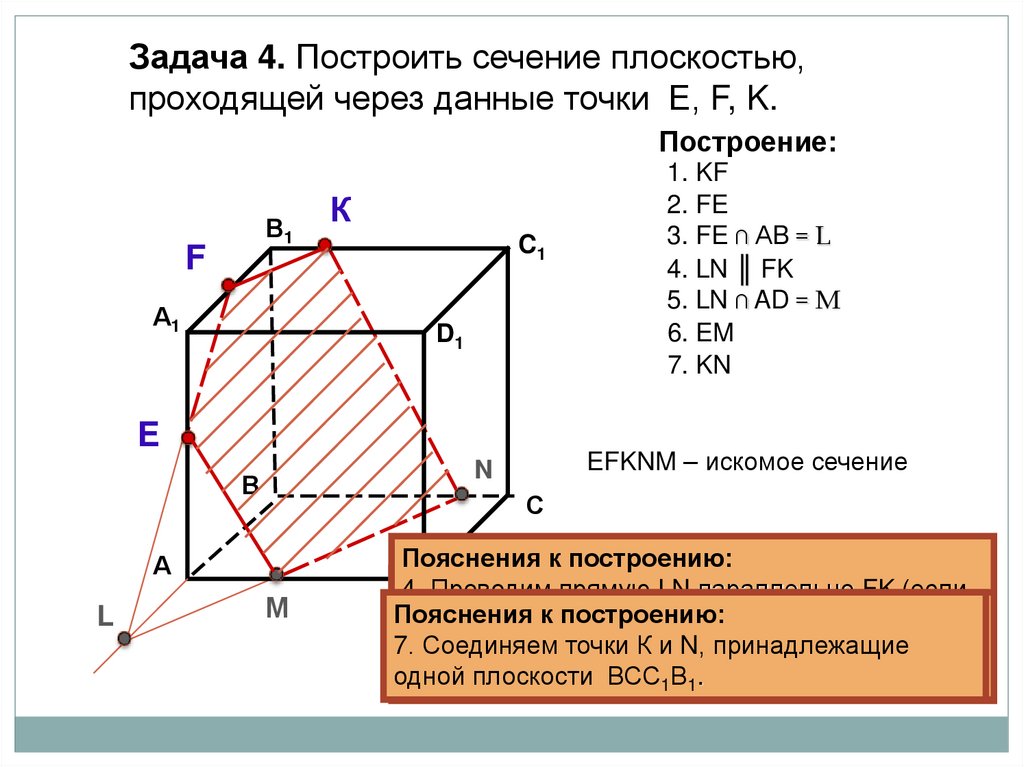
Задача 4. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
Построение:
В1
F
А1
К
C1
D1
E
С
А
L
EFKNM – искомое сечение
N
В
1. KF
2. FE
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD = M
6. EM
7. KN
М
Пояснения к построению:
4.
Проводим
LN параллельно FK (если
Пояснения
кпрямую
построению:
Пояснения
к построению:
Пояснения
Пояснения
кккпостроению:
построению:
секущая
плоскость
3.DПрямые
FE
и АВ,пересекает
лежащие
в принадлежащие
одной
плоскости
Пояснения
построению:
1. Соединяем
2.
точки
K и E,
F
F,
принадлежащие
7.
6.
Соединяем
точки
точкиграни,
КЕиивN,
М,то
принадлежащие
принадлежащие
противоположные
она
их
АА
В, пересекаются
L пересекает
. в точке M.
5.Соединяем
Прямая
LN
пересекает
AD
1В1одной
плоскости
А1точке
АА
Вребро
В
11С
1В.
1D1.
одной
одной
плоскости
плоскости ВСС
АА
по параллельным
отрезкам).
1D
1В
1D.
1.

24.

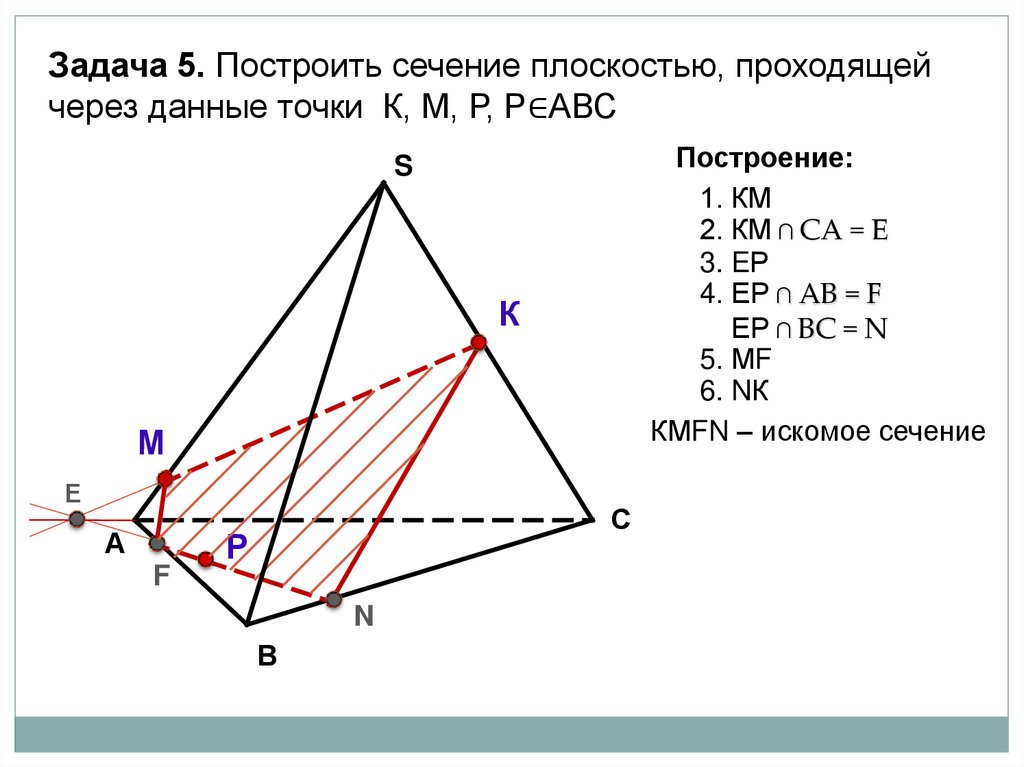
Задача 5. Построить сечение плоскостью, проходящей
через данные точки К, М, Р, Р∈АВС
Построение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение
S
К
М
Е
А
F
С
Р
N
В

25.

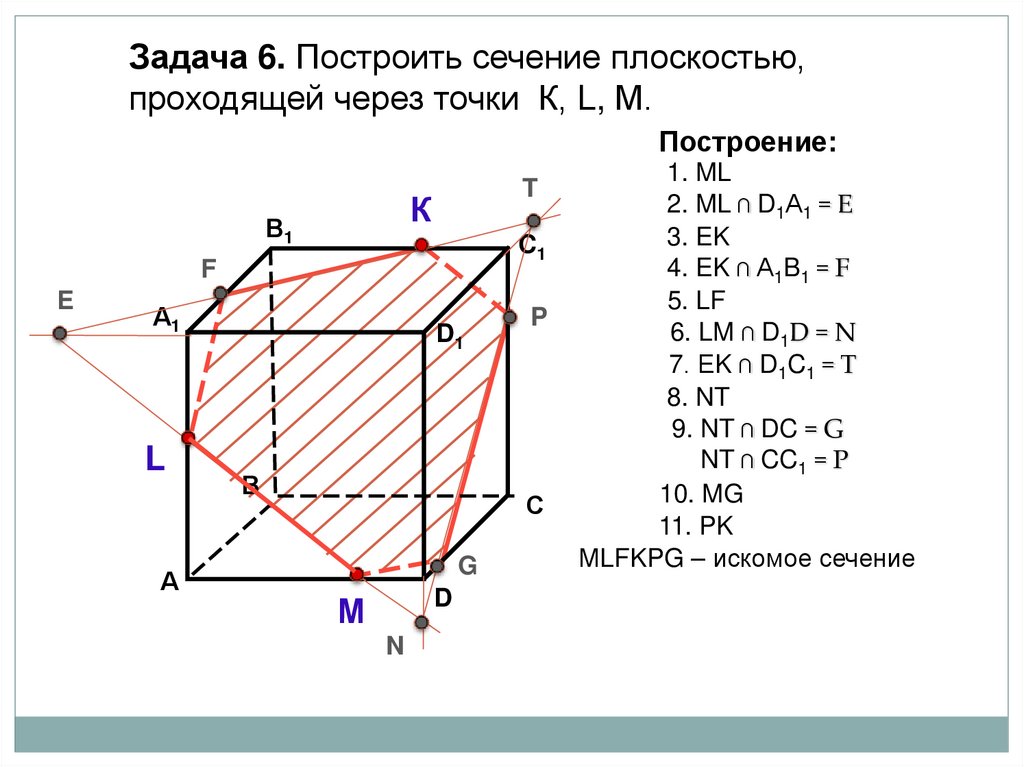
Задача 6. Построить сечение плоскостью,
проходящей через точки К, L, М.
Построение:
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
D
М
N
1. ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 = F
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение

26.

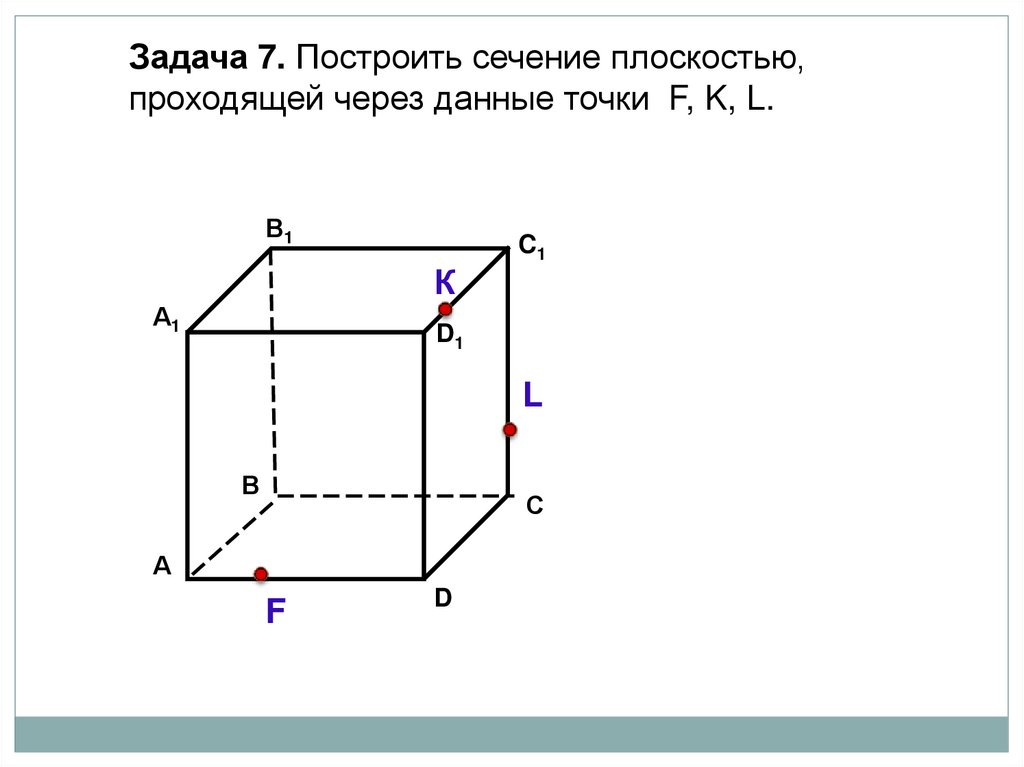
Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
В1
К
А1
C1
D1
L
В
С
А
F
D

27.

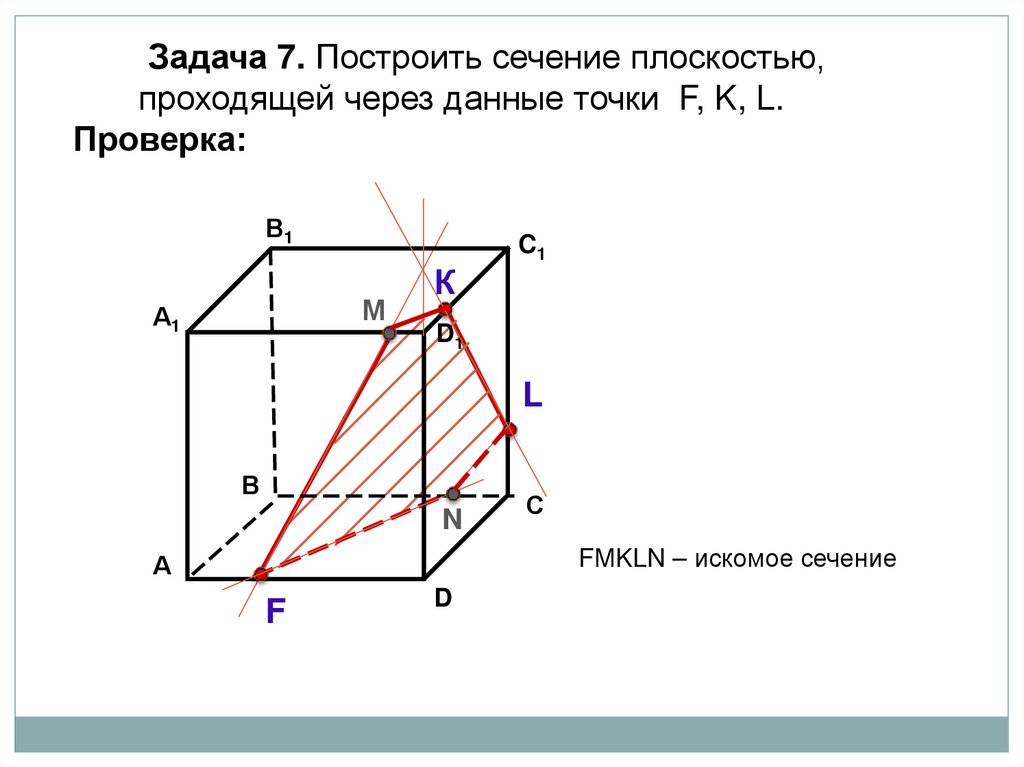
Задача 7. Построить сечение плоскостью,
проходящей через данные точки F, K, L.
Проверка:
В1
М
А1
К
C1
D1
L
В
N
С
FМKLN – искомое сечение
А
F
D