Лекция_16_Понятие_определённого_интеграла,_его_геометрический_смысл

1. Лекция 16. Понятие определённого интеграла, его геометрический смысл и свойства, интеграл с верхним пределом. Формула Ньютона –

Лейбница. Полярная система координат;
уравнения кривых в полярной системе
координат.
1

2.

Определенный интеграл
§ 1. Площадь криволинейной трапеции.
Определение 1. Пусть функция y = f (x)
непрерывна и неотрицательна на [a,b].
Криволинейной трапецией будем называть
фигуру на плоскости, ограниченную прямыми
x = a, x = b, y = 0 и кривой y = f (x).

3.

Задача (о площади криволинейной трапеции).
Вычислить площадь криволинейной трапеции P.
Вопрос: что такое площадь криволинейной
трапеции? Что такое площадь многоугольника
мы знаем.
Схема «Т»
1. Разобьём [a,b] точками
a = x0 < x1 < x2 < … < xn-1 < xn = b
на конечное число частей. Точки берем
произвольно. Таким образом, получаем
разбиение
T = {[x0,x1], [x1,x2], …, [xn-1,xn]}
отрезка [a,b] на более мелкие отрезки.

4.

Точки x0, x1, …, xn называются точками
разбиения, а полученные отрезки – отрезками
разбиения.
2. Обозначим через
x1 = x1 – x0, x2 = x2 – x1, …, xn = xn – xn-1,
где xi – длина i-того отрезка (i =1, 2, …, n).
Введем по определению:
(T) = max xi
1 i n
Назовем (T) рангом разбиения T. Это
наибольшая из длинн отрезков разбиения.
3. Выберем в каждом из отрезков разбиения
произвольно по точке:

5.

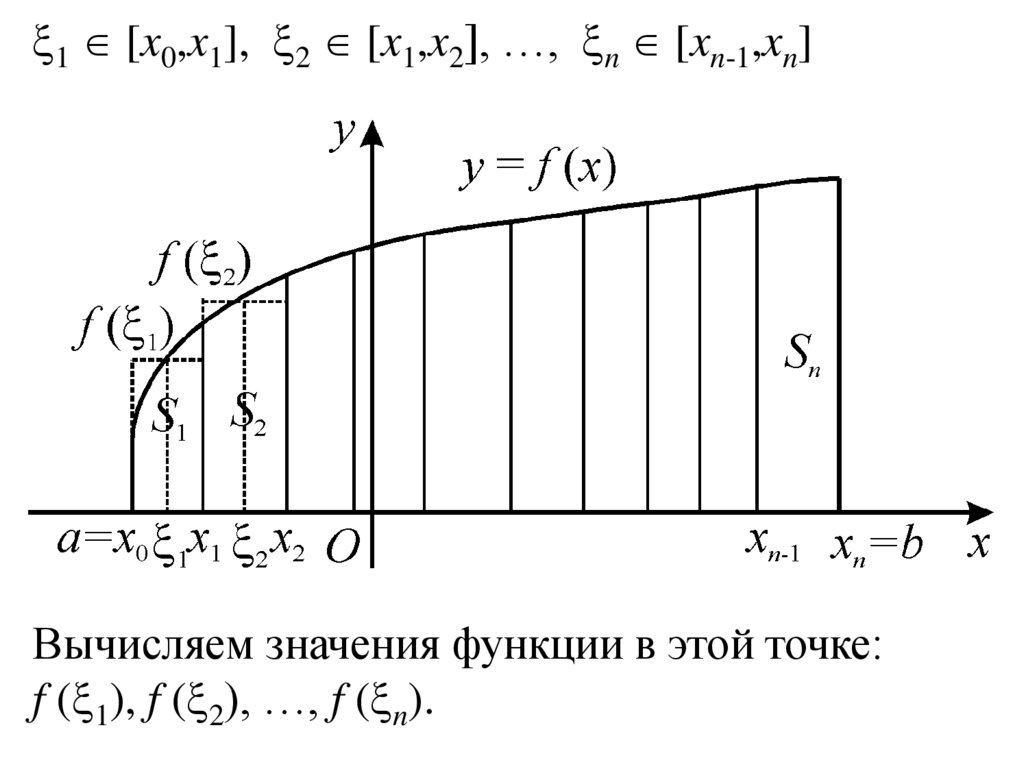
1 [x0,x1], 2 [x1,x2], …, n [xn-1,xn]
Вычисляем значения функции в этой точке:
f ( 1), f ( 2), …, f ( n).

6.

Строим интегральную сумму:
S(T ) = f ( 1) x1 + f ( 2) x2 + … + f ( n) xn =
n
f i xi
i 1
S(T ) называется интегральной суммой функции
f по данному разбиению T.
Таким образом, геометрически S(T ) – площадь
ступенчатой фигуры (сумма площадей
прямоугольников).
S(T ) – это число.
Разбивая по другому отрезок [a,b] на части и
выбирая по другому точки i всякий раз будем

7.

получать новые интегральные суммы вида S(T ).
Таким образом, можно говорить о переменной
интегральной суммы на данном отрезке. Но эта
переменная величина более сложной природы,
нежели те, что были до сих пор. Введем понятие
предела этой переменной величины.
Определение 2. Число I называется пределом
переменной интегральной суммы S(T ) функции
f (x) на отрезке [a,b] при (T) 0 если:
R+ R+ T ( (T) < S(T ) – I < )
n
Обозначают: lim S (T ) lim f i xi
T 0
T 0 i 1

8.

Этот предел не зависит от характера разбиения и
выбора точек i.
Конец схемы «Т»
Замечание 1. Высказывание в определении 2
означает, что когда (T) 0 S(T ) I.
Замечание 2. Если (T) 0, то очевидно, что
число отрезков разбиения n стремится к
бесконечности.
Определение 3. Пусть функция y = f (x)
непрерывна и неотрицательна на отрезке [a,b] и
P – ее криволинейная трапеция. Если существует конечный предел
n
I lim f i xi
T 0 i 1

9.

то он называется площадью криволинейной
трапеции.
Замечание 3. Введенный нами предел
переменной интегральной суммы обладает
всеми обычными свойствами предела.
§ 2. Понятие определенного интеграла.
Условие его существования.
Пусть y = f (x) произвольная функция на отрезке
[a,b]. Применим к этой функции схему «Т»
(разбиение Т, (T), i, f ( i), S(T ), lim S (T ) ).
T 0

10.

Определение 4. Если существует конечный
предел I переменной интегральной суммы, не
зависящий от вида разбиения и выбора точек i,
то этот предел называется определенным
интегралом (или интегралом Римана) функции f
на отрезке [a,b].
b
Обозначается: f ( x) dx.
a b
n
a
T 0 i 1
Таким образом: f ( x)dx lim f i xi
где: f (x) – подынтегральная функция,
f (x)dx – подынтегральное выражение,

11.

a – нижний предел интегрирования,
b – верхний предел интегрирования,
[a,b] – отрезок интегрирования.
Функция f (x) называется интегрируемой по
Риману на данном отрезке.
Геометрический смысл определенного
интеграла.
Возвращаясь к задаче о площади криволинейной
трапеции, можем утверждать, что для
неотрицательной и непрерывной функции
b
y = f (x) на отрезке [a,b], f ( x)dx численно равен
a
площади соответствующей криволинейной
трапеции

12.

Замечание 4. В отличие от неопределенного
интеграла, который представляет собой
семейство функций, определенный интеграл
b
f ( x)dx представляет собой вещественное
a
число.
Теорема 1. (Необходимое условие
интегрируемости по Риману). Если функция
y = f (x) интегрируема по Риману на отрезке
[a,b], то она ограничена на этом отрезке.
Без доказательства.

13. § 3. Параметрическое задание кривых и функций.

На первый взгляд ,
плоская кривая
представляется простым объектом. Её мы
можем мыслить как траекторию движения
точки. При детальном рассмотрении это
понятие оказывается одним из самых
сложных. Возникает вопрос: всякая ли кривая
может быть задана y = f (x) ? Ответ: конечно
нет .
13

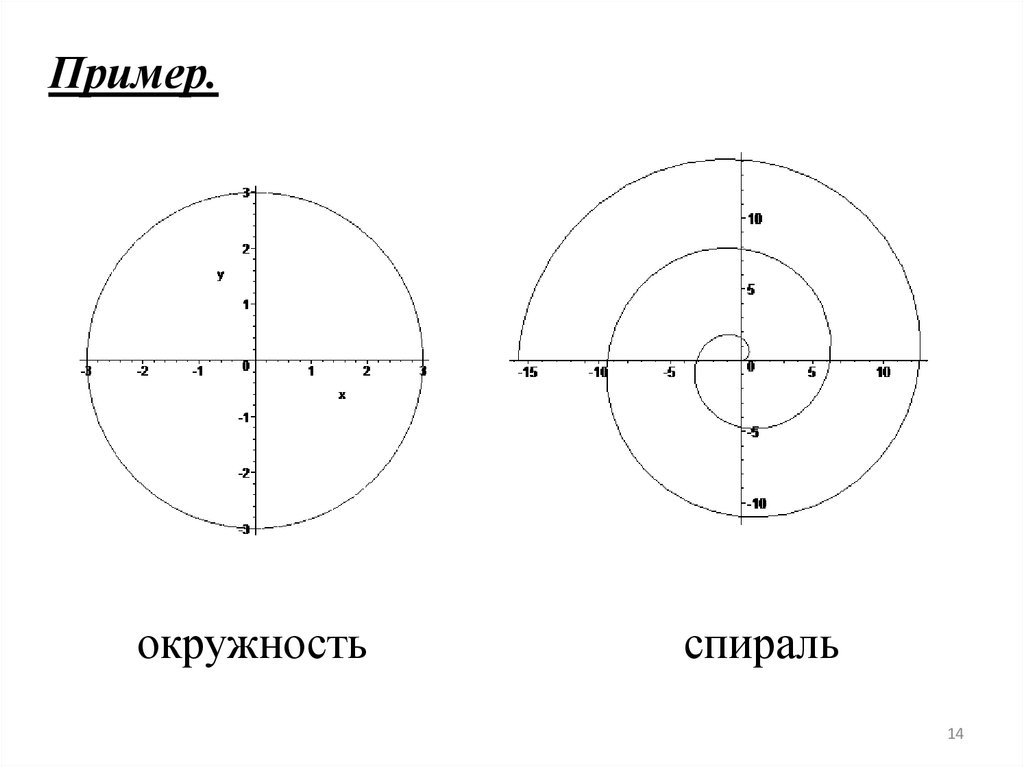
14.

Пример.
окружность
спираль
14

15.

Однако эти кривые могут быть заданы
полярными уравнениями в ПСК .
Рассмотрим окружность с центром в начале
координат и радиусом R.
M(x ; y) окр. (O:R)
x = R cos t
(1)
Из чертежа:
y = R sin t
Легко видеть, что окружность есть множество
всех точек, координаты которых
удовлетворяют (1).
(1) называется параметрическим уравнением
данной кривой, а t – параметром.
15

16.

Определение. Пусть
x=Φ(t)
(2) ,
y=Ψ(t)
где t T– промежутки, Φ ( f ) и Ψ ( t ) непрерывны
на T.
Непрерывной плоской кривой называется
множество всех точек M (x ; y), координаты
которых удовлетворяет уравнению (2) , t при этом
называется параметром, а само задание кривой с
помощью (2) называется параметрическим.
16

17.

Замечание 1: В рассмотренном примере роль
параметра играет центральный угол. В других
случаях параметром может быть время и другие
вещи по смыслу.
Замечание 2: Явное задание кривой ( y = f (x),
x [a ; b] ) является частным случаем
параметрического значения. Действительно, мы
можем записать параметрическое уравнение
кривой f в следующем виде:
x=t
, t [a ; b]
y = f (t)
17

18.

Замечание 3: Полярное задание кривой с
помощью уравнения ( p = f (Ѳ), Ѳ [α, β] )
также является частным случаем
параметрического. Действительно, известны
формулы перехода от полярной системы
координат к декартовой , а именно :
x = ρ cos Ѳ
y = ρ sin Ѳ
x = f (Ѳ) cos Ѳ
, Ѳ [α, β]
y = f (Ѳ) sin Ѳ
18