Похожие презентации:
Определённый интеграл
1. ТЕМА 8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
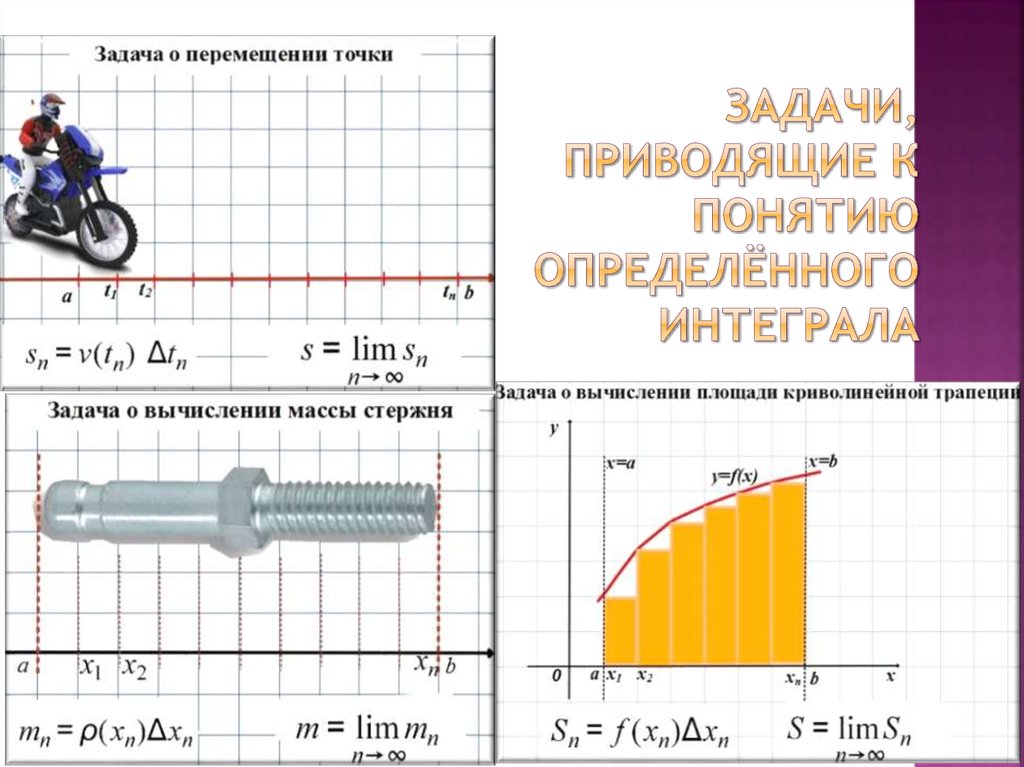
2. Задачи, приводящие к понятию определённого интеграла
3.
Решение различных задач привелок одной и той же математической
модели:
Для функции y=f(x) на отрезке [a;b]:
1.Разбить отрезок [a;b] на n равных частей
2.Составить сумму Sn =f(x0)·∆x0+…+ f(xn)·∆xn
3.Вычислить предел этой суммы при n→∞
4.
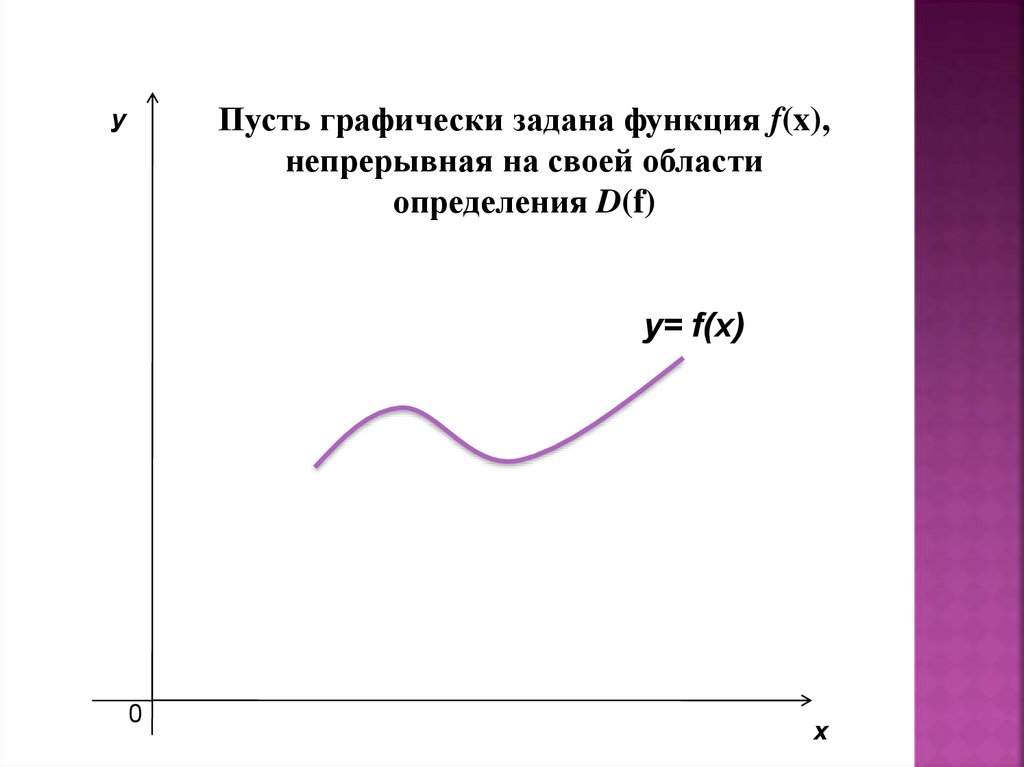
Пусть графически задана функция f(x),непрерывная на своей области
определения D(f)
y
у= f(x)
0
x
5.
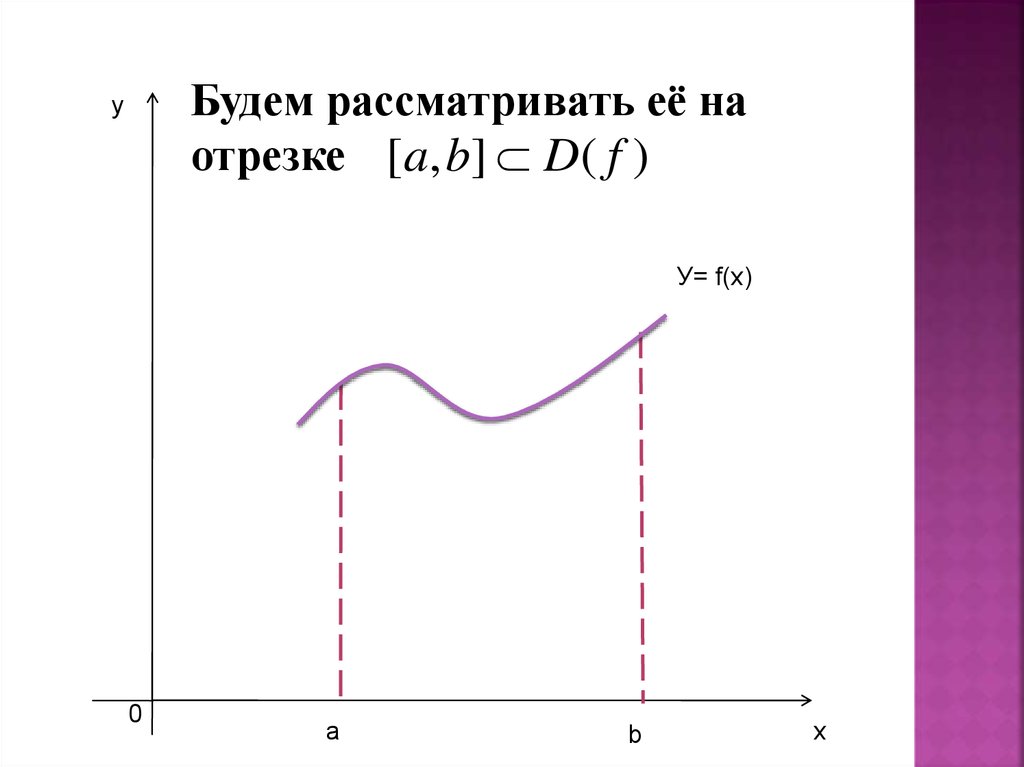
Будем рассматривать её наотрезке [a, b] D( f )
y
У= f(x)
0
а
b
x
6.
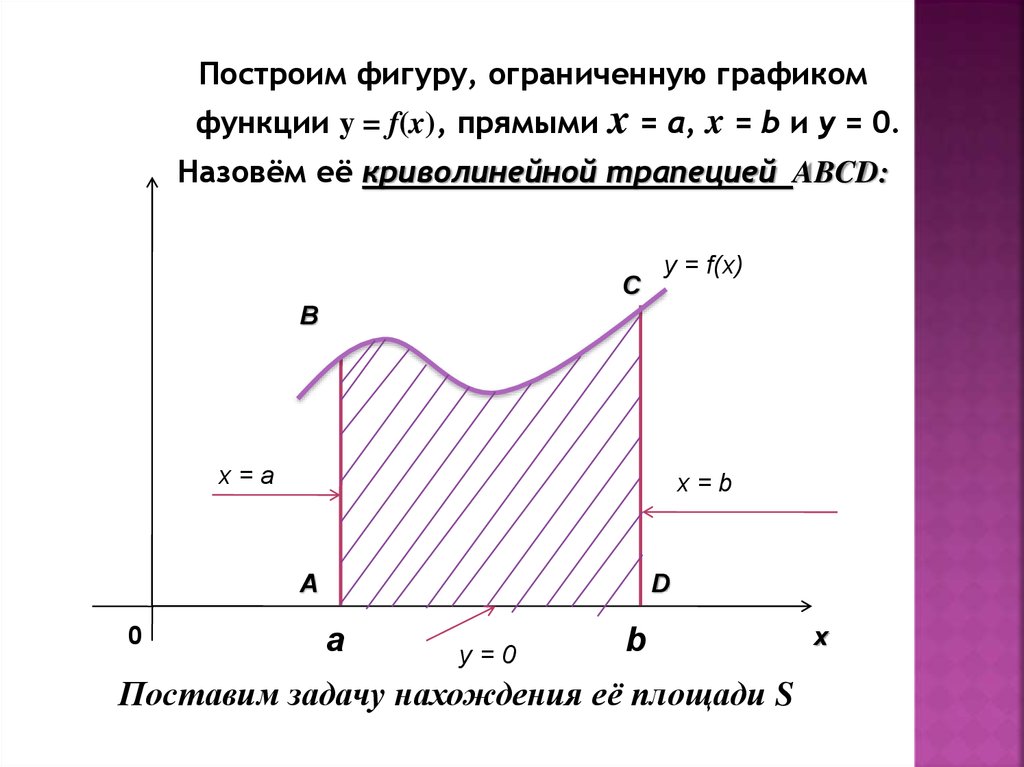
Построим фигуру, ограниченную графикомфункции y = f(x), прямыми
x = а, x = b и у = 0.
Назовём её криволинейной трапецией ABCD:
C
у = f(x)
B
x=a
x=b
A
0
D
а
y=0
b
Поставим задачу нахождения её площади S
x
7.
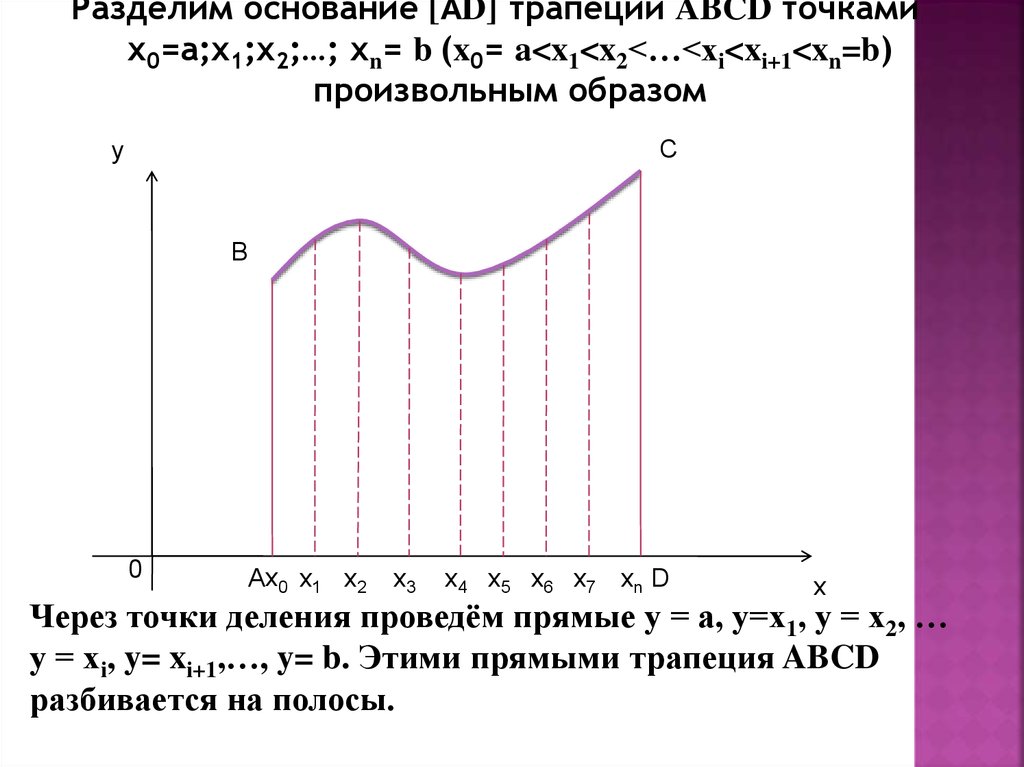
Разделим основание [АD] трапеции ABCD точкамих0=а;х1;х2;…; хn= b (x0= a<x1<x2<…<xi<xi+1<xn=b)
произвольным образом
С
y
В
0
Аx0 x1 x2
x3
x4 x5 x6 x7 xn D
x
Через точки деления проведём прямые у = а, у=х1, у = х2, …
у = хi, y= xi+1,…, y= b. Этими прямыми трапеция ABCD
разбивается на полосы.
8.
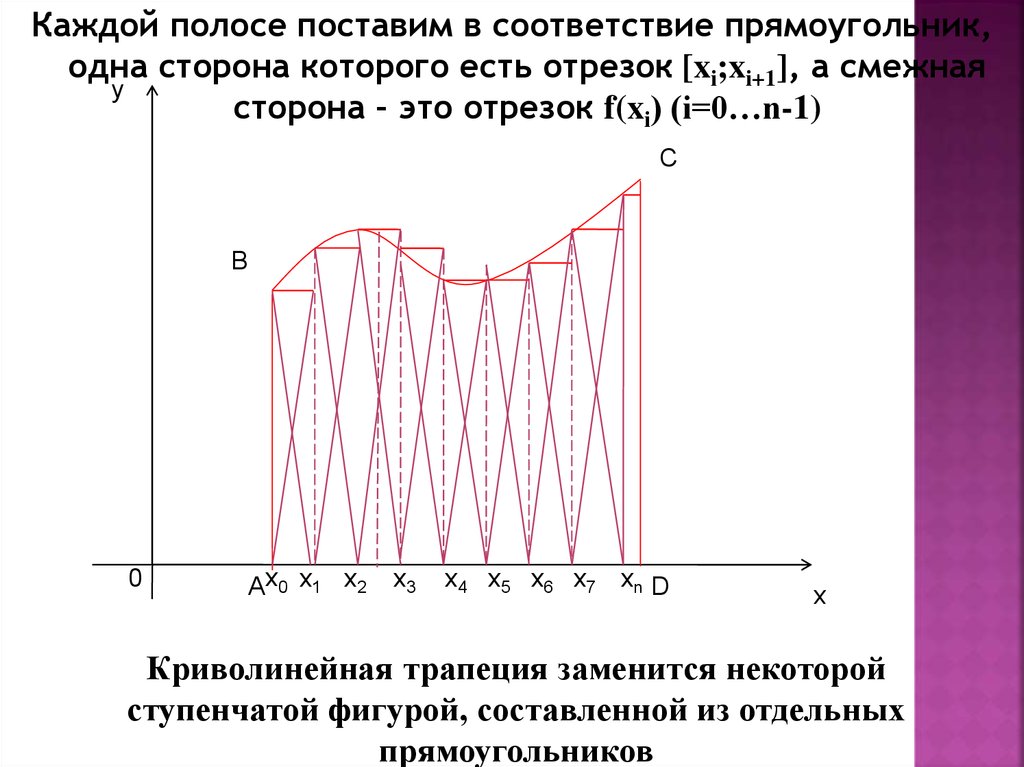
Каждой полосе поставим в соответствие прямоугольник,одна сторона которого есть отрезок [xi;xi+1], а смежная
y
сторона – это отрезок f(xi) (i=0…n-1)
С
В
0
Аx0 x1 x2
x3
x4 x5 x6 x7 xn D
x
Криволинейная трапеция заменится некоторой
ступенчатой фигурой, составленной из отдельных
прямоугольников
9.
yС
В
0
A x0
x1 x2
x3
x4 x5 x6 x7 xn D
x
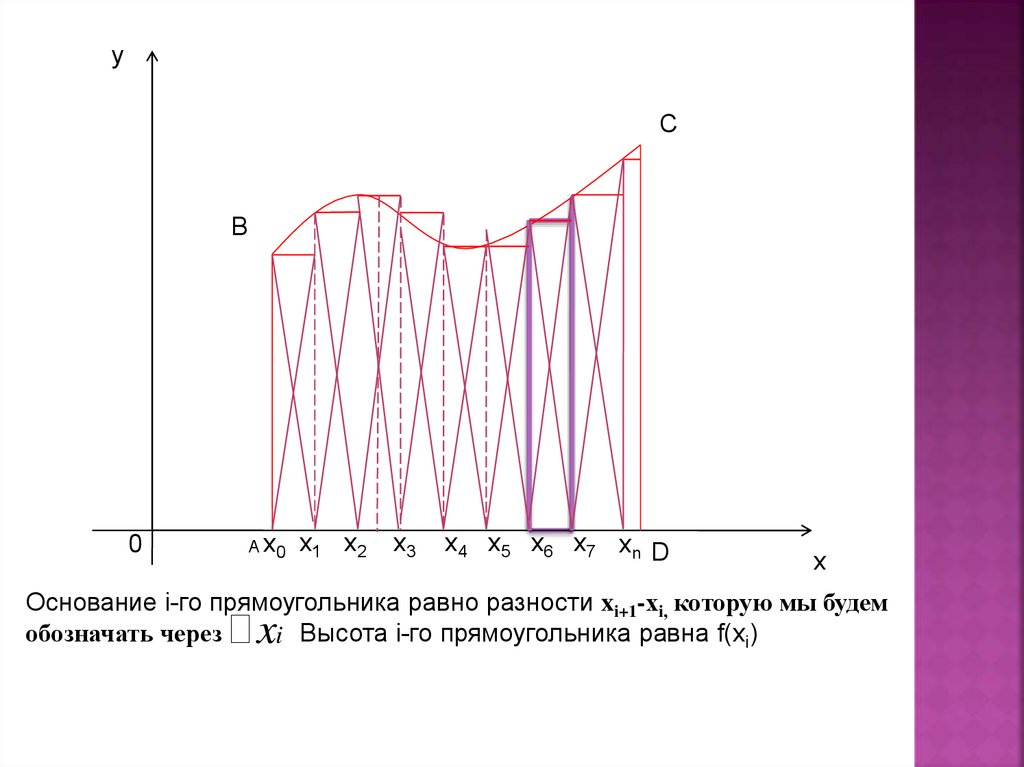
Основание i-го прямоугольника равно разности xi+1-хi, которую мы будем
обозначать через
i Высота i-го прямоугольника равна f(xi)
x
10.
Площадь i-го прямоугольника равна:Si f ( xi ) xi
Сложив площади всех прямоугольников,
получаем приближенное значение площади S
криволинейной трапеции:
n 1
S f ( xi ) xi
i 0
11.
Точное значение площади S получается какпредел суммы площадей всех прямоугольников
S lim
x 0
n
f ( x ) x
i
i 0
i
Для обозначения предельных сумм вида
f(xi) xi немецкий учёный В.Лейбниц ввёл
символ
- интеграл функции f(x) от а до b
b
n
f ( x)dx lim f ( x ) x
a
x 0
i 0
i
i
12.
Если предел функции f(x) существует,то f(x) называется
интегрируемой на отрезке [a, b].
Числа а и b называются нижним и верхним
пределом интегрирования.
При постоянных
пределах интегрирования
определённый интеграл
представляет собой определённое число.
13.
f (x)- подынтегральная функция;
f ( x)dx - подынтегральное выражение;
a - нижний предел интегрирования;
b - верхний предел интегрирования.
14.
Теорема. Определенный интеграл независит от выбора первообразной
для интегрирования функции.
Теорема. Для всякой, непрерывной на
отрезке [ a; b] функции, существует
соответствующий определенный
интеграл.
Доказательство основано на теореме
Коши, т.е. существует определенный
интеграл, значит, существует разность
значений первообразной.
15.
Свойства определенного интегралаПусть на отрезке (a; b) существует
определенный интеграл
b
a
f ( x)dx F (b) F (a), где F ' ( x) f ( x)
b
b
a
a
a
1. f ( x)dx f (t )dt
2. f ( x)dx 0
a
16.
ba
a
b
3. f ( x)dx f ( x)dx
4. Константу как множитель можно
выносить за знак определенного
интеграла.
5. Определенный интеграл от
суммы конечного числа
непрерывных функций равен сумме
определенных интегралов от этих
функций.
17.
6. Если подынтегральная функция fнеотрицательна, то и определенный
интеграл от нее неотрицателен.
(x)
7. Теорема о среднем
Если f (x ) - непрерывная функция, то
определенный интеграл равен:
b
a
f ( x)dx (b a) f (c), c (a; b)
18.
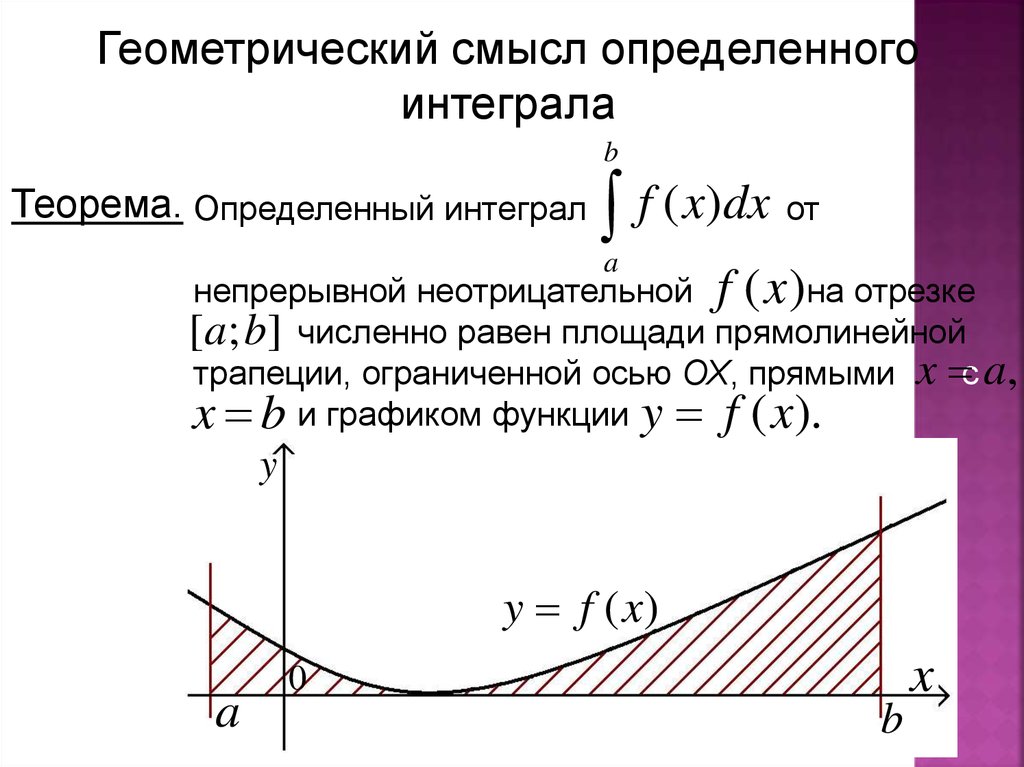
Геометрический смысл определенногоинтеграла
b
Теорема. Определенный интеграл
f ( x)dx от
a
непрерывной неотрицательной f (x )на отрезке
[иa; b] численно равен площади прямолинейной
трапеции, ограниченной осью ОХ, прямыми x с a,
xи b и графиком функции y f (x).
y
y f (x)
a
x
0
b
19.
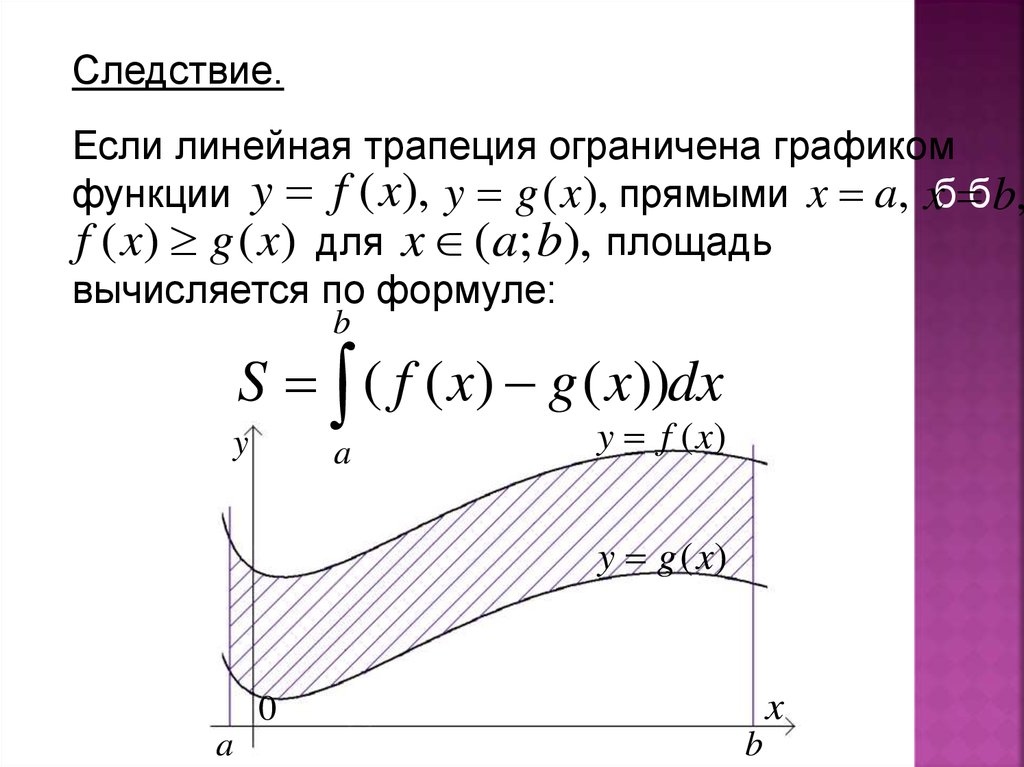
Следствие.Если линейная трапеция ограничена графиком
функции y f (x), y g (x), прямыми x aб, xб бb,
бf ( x) g ( x) для x ( a; b), площадь
вычисляется по формуле:
b
S ( f ( x) g ( x))dx
y
a
y f (x)
y g (x)
x
0
a
b
20.
Связь и отличие определенных инеопределенных интегралов
Связь:
Как в неопределенном, так и
в определенном интеграле
нужно находить
первообразную для функции
f (x ).
21.
Отличие:Неопределенный интеграл –
общее выражение для всех
первообразных, определенный
интеграл – это число.
22. Теорема о существовании определенного интеграла
Теорема.Если функция f x непрерывна на
отрезке a, b , то
n
f xi xi
lim
max xi 0 i 1
существует и конечен, т.е.
b
существует и конечен f x dx .
a
23. Свойства определенного интеграла
a1. f x dx 0 ;
a
b
2. dx b a ;
a
b
a
3. f x dx f x dx ;
a
b
b
4. f1 x f 2 x dx f1 x dx f 2 x dx ;
a
b
b
a
a
24. Свойства определенного интеграла
bb
a
b
a
5. Kf x dx K f x dx ;
c
b
a
c
6. f x dx f x dx f x dx ;
a
b
7. f x dx 0 , если f x 0 .
a
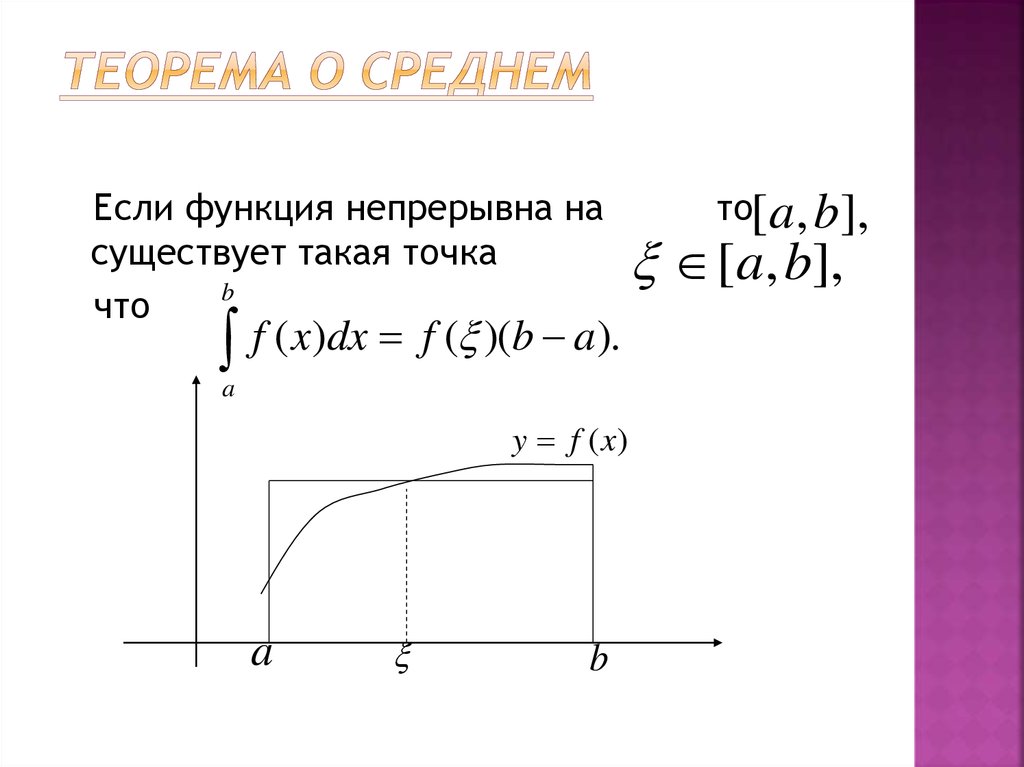
25. Теорема о среднем
Если функция непрерывна насуществует такая точка
b
что
f ( x)dx f ( )(b a).
a
y f (x)
a
b
то[ a, b],
[a, b],
26. Вычисление определенного интеграла
Теорема.Пусть F x - первообразная функции f x .
b
Тогда f x dx F b F a .
a
Эту формулу называют формулой
Ньютона-Лейбница, из которой следует,
что для вычисления определенного
интеграла необходимо найти
первообразную подынтегральной функции.
27. Формула Ньютона-Лейбница
ba
Исаак Ньютон
1642-1727
f ( x)dx F (b) F (a ),
где F(x) – первообразная
для функции f(x) Или
b
b
a
a
f ( x)dx F ( x)
Формула Ньютона-Лейбница:
b
b
f ( x)dx F ( x)
a
F (b) F (a)
a
Готфрид Лейбниц
1646-1716
28. Вычисление определённого интеграла
Вычислить интеграл:2
2
2
2
2 Формула
Постоянный
множитель
Ньютона-Лейбница:
dx можно
от
суммы
функций
равен
3 вынести
( 2 Интеграл
3x3 1за
)dx
2
3
x
dx
dx
2
знак
интеграла
сумме интегралов
x
x
1
1
2
1
4 2
1
4
2
1
x
2 3x
2
b 2( ) 3
x b1 ( b x)
xf ( x1 b)dx4 1F ( x) b Fx (b)4 F (a )1
( f ( x) gkf( x( x)))dx k f (fx()xdx
)dx g ( x)dx
a
3 a aa
1 a
a
a
( 1 12 2) (2 1) 11
4
4
1
Ответ : 11
4
b
b
29. Пример
Вычислить3
e
x .
3 dx
0
0
3
1 3 1 0
e 3 e 3
3
0
0
1 e
1
1
3 e 1 3 1 3
e
e
x
1
3
3 x
e 3 dx e 3 dx
1
x
3e 3
30. Вычисление интеграла
Теорема (Замена переменной вопределенном интеграле).
Пусть f x непрерывна на a, b , а
функция x t непрерывна вместе
со своей производной t на
отрезке , , причем a ,
b .
31.
bТеорема. Дано:
f ( x)dx, f ( x) (a; b).
a
Введем новую переменную,
связанную с
x формулой x (t ),
(tb) непрерывна на отрезке ; ,
при этом ( ) a,
( ) b
b
a
Тогда :
f x dx f t t dt
32.
тогдаb
a
x (t )
dx ' (t ) dt
f ( x)dx
x a b
t
f ( (t )) ' (t )dt F (t ) F ( ) F ( )
33. Пример
x 1 tx 1 t 2
3
xdx
2 t2
x t 1, dx 2tdt
1
x 1
x 0, t 1
0
2
1
2tdt
t
x 3, t 2
2
t
8
1
2 t 1 dt 2 t 1 dt 2
t
2 2 1
3
1
1
3
3
1
2
2
2
2
3
1
4 8
8
7
2 2 1 2 1 2
3
3 3
3
3
34.
Теорема (Интегрирование почастям в определенном
интеграле).
Если функции u u x , v v x и их
производные u x и
v x непрерывны на отрезке a, b , то
b
b
a
a
b
udv u v vdu .
a
35. Пример
dxu ln x, du
e e dx
x x ln x 1 x
ln xdx
x
1
1
dv dx, v x
e
x ln
e
x1
e
e
dx e ln e ln 1 x 1
1
e e 1 1
36. Несобственный интеграл
Замечание.f x dx не является определенным интегралом.
a
Считается по определению, что
b
f x dx lim f x dx . Если этот предел
a
b a
конечен, то f x dx , называемый
a
несобственным, сходится.
Если же этот предел не является конечным, то
интеграл расходится.
37. Пример
. Вычислить несобственный интеграл0
xdx
x2 4
(или установить его расходимость)
b
b
xdx
1
d ( x 2 4) 1
.
2
lim
lim ln( x 4)
x
0
2
4
2 b 0 x 2 4
2 b
0
1
lim (ln(b 2 4) ln 4)
2 b
Этот несобственный интеграл расходится.
38. Пример
Несобственный интеграл0
dx
2
x 4
1
b 1
lim arctg arctg ( )
b 2
2 2
2 2 4
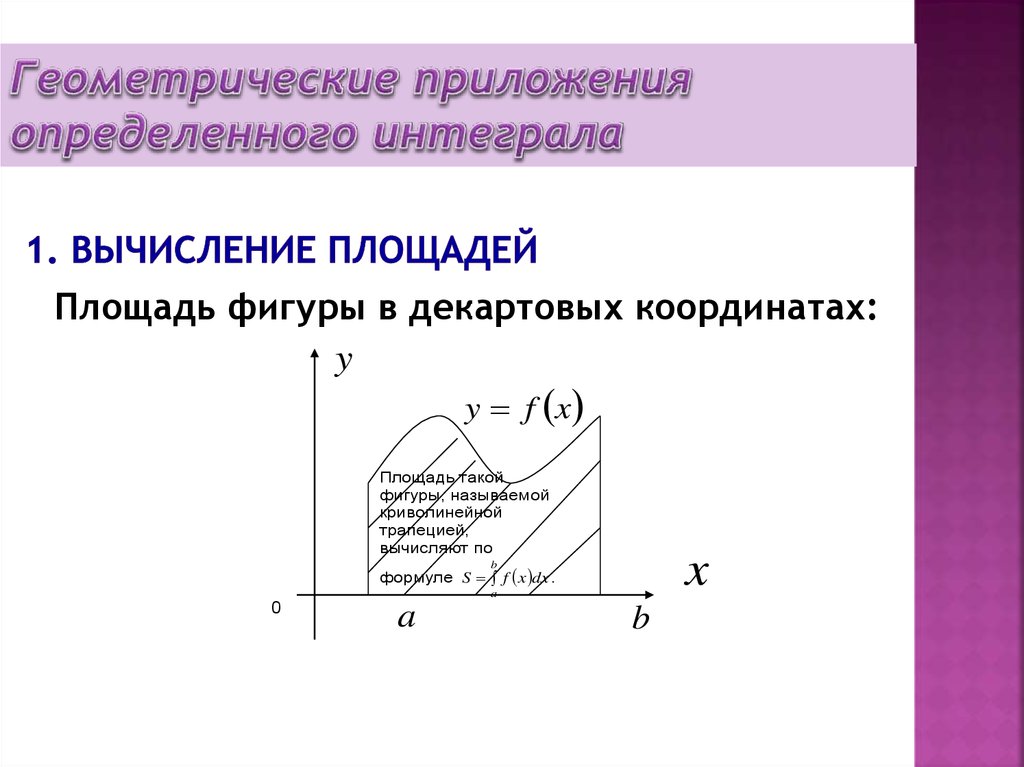
39. 1. Вычисление площадей
Площадь фигуры в декартовых координатах:y
y f x
Площадь такой
фигуры, называемой
криволинейной
трапецией,
вычисляют по
x
b
формуле S f x dx .
a
0
a
b
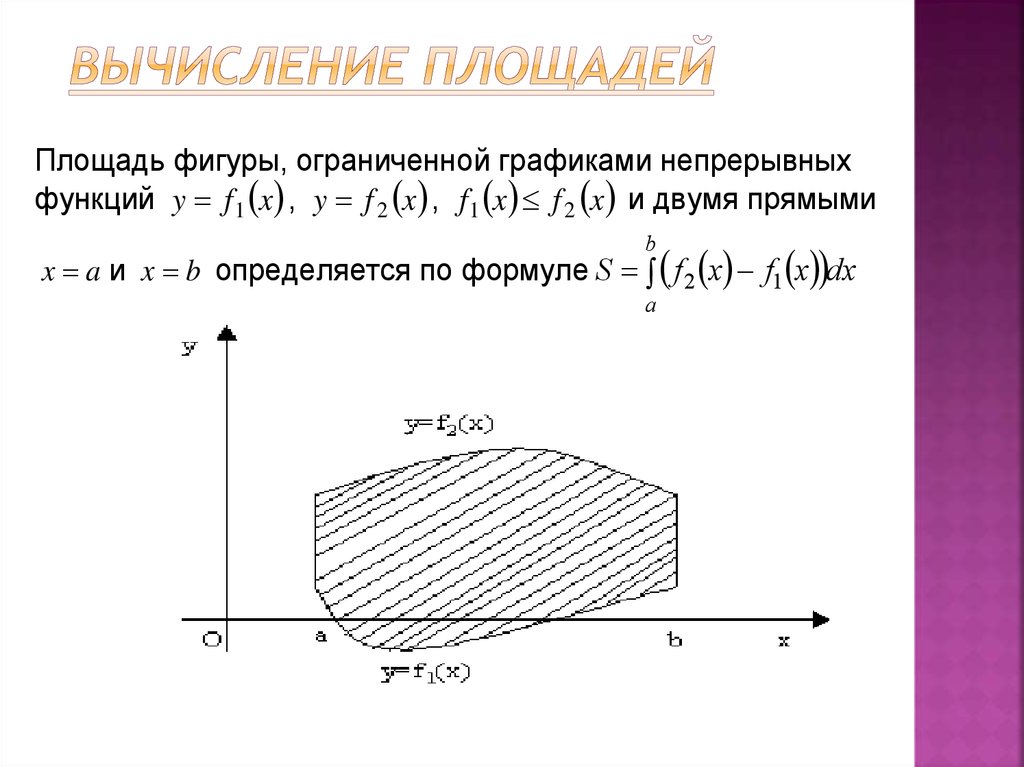
40. Вычисление площадей
Площадь фигуры, ограниченной графиками непрерывныхфункций y f 1 x , y f 2 x , f1 x f 2 x и двумя прямыми
b
x a и x b определяется по формуле S f 2 x f1 x dx
a
41. Вычисление площадей
В случае параметрического заданиякривой, площадь фигуры, ограниченной
прямыми x a, x b, осью Ох и кривой
x (t ), y (t ), вычисляют по
формуле
t2
S (t ) (t )dt ,
где пределы интегрирования
определяют из
t1
.
уравнений
.
a (t1 ), b (t 2 )
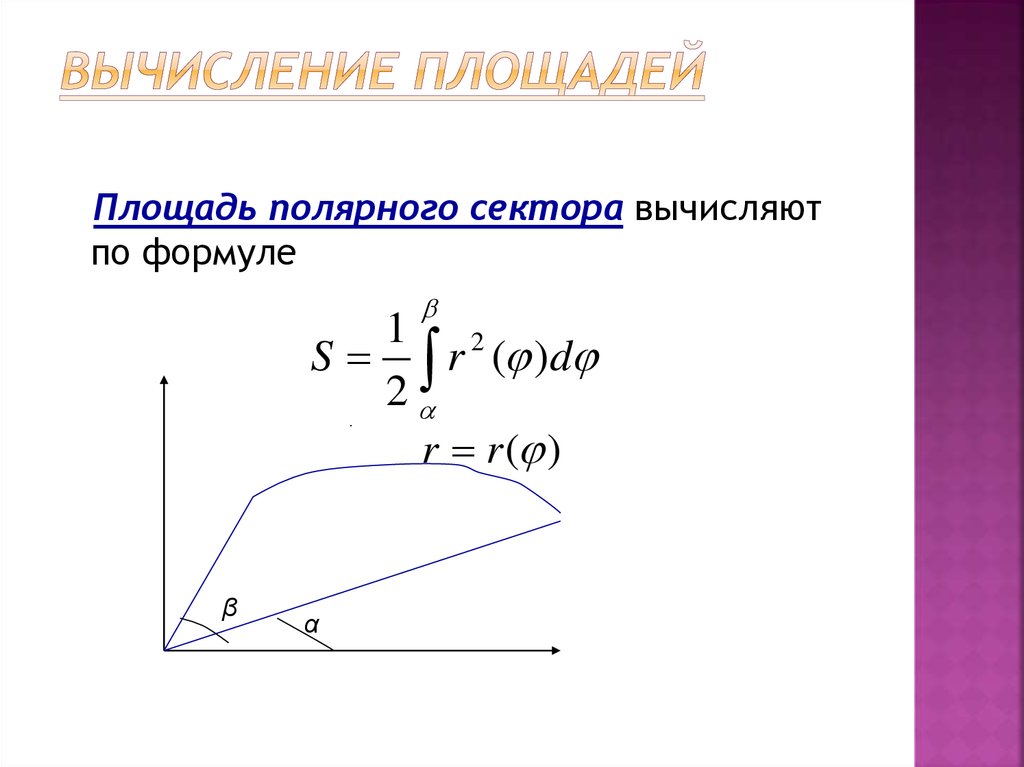
42. Вычисление площадей
Площадь полярного сектора вычисляютпо формуле
1 2
S r ( )d
2
r r ( )
.
β
α
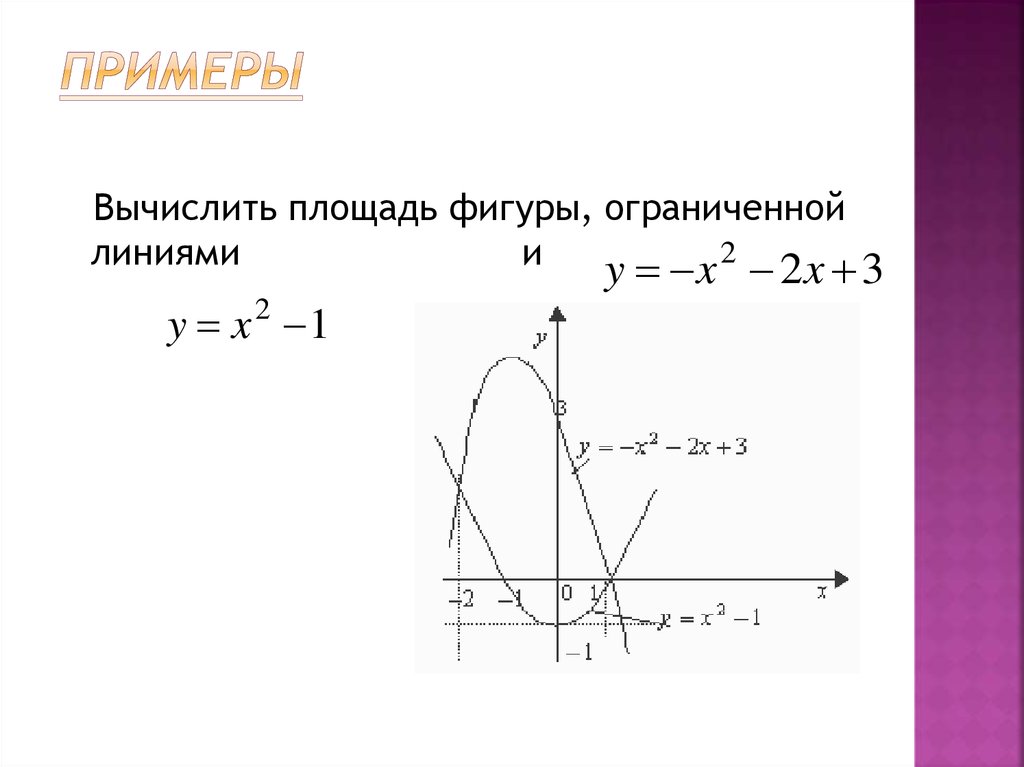
43. Примеры
Вычислить площадь фигуры, ограниченнойлиниями
и
y x 2 2x 3
y x 2 1
44. Продолжение
ПолучимS x 2 x 3 x 1 dx 2 x
1
2
1
2
1
x
x
2 x x 2 dx 2
2x
3
2
2
2
1
2
3
2
2 x 4 dx
2
2
2
1 1
8
8 4
1 1
2 2 4 2 2 6
3
3 2
3 2
3 2
1
9
2 3 8 2 9
2
2
45. Примеры
x2 y2Найти площадь эллипса 2 2 1 .
a
b
Параметрические уравнения эллипса
x a cos t , y b sin t.
0
S 4 b sin t ( a sin t )dt
/2
у
/2
b
4ab sin tdt 4ab
2
х
о
/2
a
0
0
1 cos 2t
dt
2
1
1
/2
4ab(t sin 2t ) 0 2ab ab.
2
2
2
46. Пример
Площадь фигуры, ограниченной2
лемнискатой Бернулли
r
и лежащей вне круга радиуса
1
2
/6
1
0 a cos 2 d 2
2
/6
0
a cos 2
2
:
r
a
2
/6
2
a
1 2
1 2
d ( a sin 2 a )
2
4
4
0
1 2
a2
3
a2
a (sin )
(
)
( 3 )
4
3 6
4 2 6
8
3
a2
S
( 3 )
2
3
47. Вычисление длины дуги
Если кривая задана параметрическимиуравнениями
, t y , тоtдлина
x
ее дуги
t2
l
t 2 t ,2 dt
–значения параметра,
где
t1
соответствующие
концам дуги .
t ,t
1 2
48. Длина дуги в декартовых координатах
Если кривая задана уравнением,y f x
b
2, где a, b–абсциссы
то l
1 f x dx
начала и конца дуги
.
a
a b
Если кривая задана
d уравнением
2
,
то
, где c d
l
1
g
y
dy
x g y
c, d–ординаты начала
и конца дуги
c
49. Длина дуги в полярных координатах
Если кривая задана уравнением вполярных координатах
, то
l
2 2 d
,
где
–значения полярного угла,
соответствующие
концам дуги .
,
50. Примеры
y xВычислить длину дуги кривой
от точки
до
.
O 0,0
B 4,8
3 1
, тогда
y x x 2
2
4
4
9
4
9 9
l 1 x dx
1 xd 1 x
4
90
4 4
0
3
2
4 2 9
1 x
9 3 4
3
2
4
0
8
10 10 1
27
3
51. Вычисление объема тела вращения.
Объем тела, образованного вращениемвокруг оси Ox криволинейной трапеции,
ограниченной кривой
, отрезком
y
f
x
оси абсцисс
и прямыми
, вычисляется по формуле a x b
.
x a , xb b
Vx π
f x dx
2
a
52. Вычисление объема тела вращения
Объем тела, образованного вращениемвокруг оси Oy фигуры, ограниченной
кривой
, отрезком оси ординат
и прямымиx g y , вычисляется по
y c, y d
формуле c y d
d
Vy
g
y
2
c
.
dy
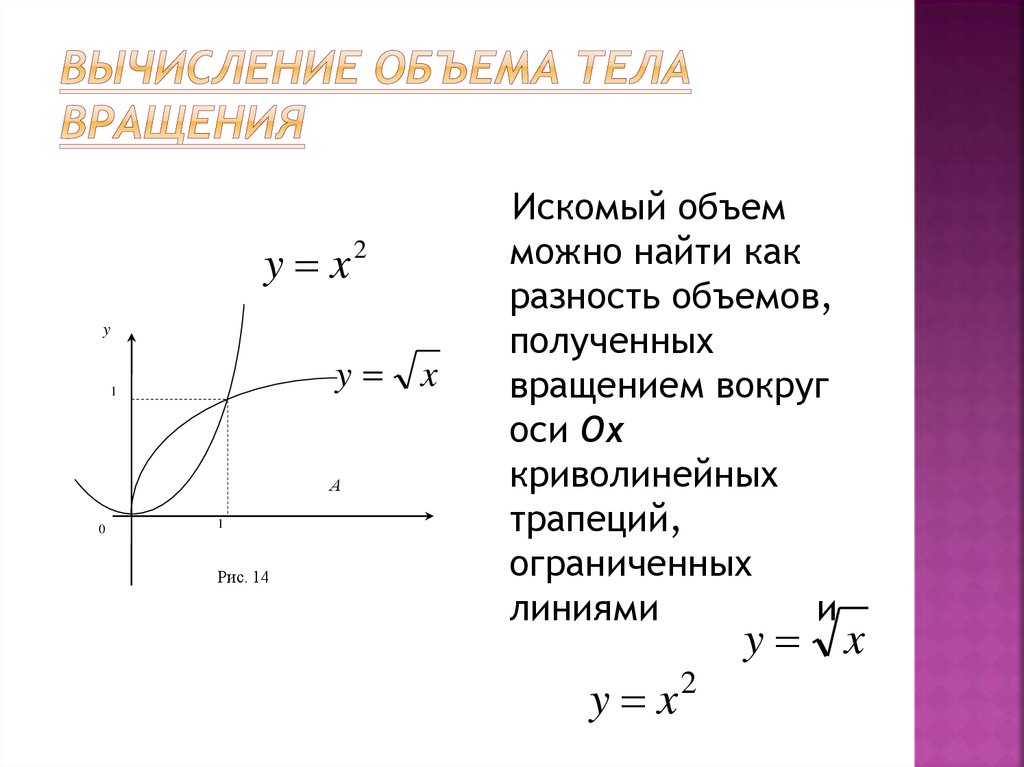
53. Вычисление объема тела вращения
y x2y
y
1
А
0
1
Рис. 14
x
Искомый объем
можно найти как
разность объемов,
полученных
вращением вокруг
оси Ox
криволинейных
трапеций,
ограниченных
линиями
и
y x
y x
2
54. Решение
Тогда1
x dx x dx
1
Vx
2
0
1
1
0
2 1
x
xdx x dx
2
0
0
4
3
2 5 10
0
2 2
5 1
x
5
0





















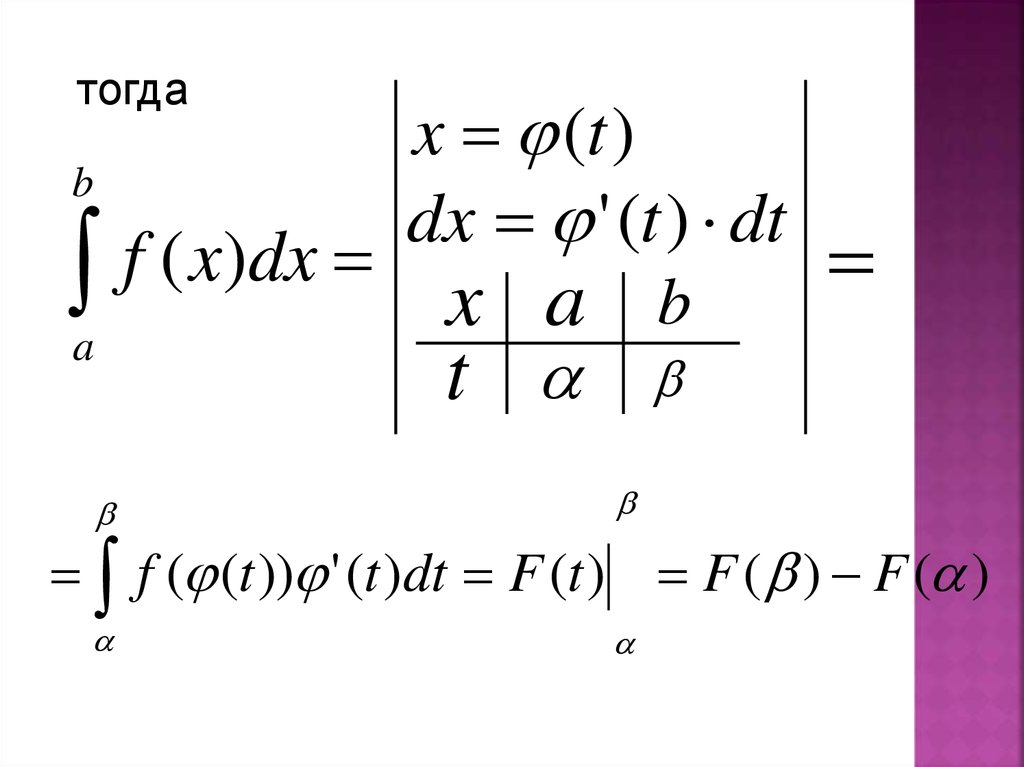

















 Математика
Математика








