ДРФ л1

1. ДОДАТКОВІ РОЗДІЛИ ФІЗИКИ (Теоретична механіка)

https://t.me/+EIC9kcsOuo01MzFi

2.

Рівень вищої освіти
Перший (бакалаврський)
Галузь знань
15 Автоматизація та приладобудування
Спеціальність
151 Автоматизація та комп’ютерно - інтегровані технології
Освітня програма
Статус дисципліни
Комп'ютерно-інтегровані системи та технології в
приладобудуванні
Нормативна
Форма навчання
очна (денна)
Рік підготовки,
семестр
Обсяг дисципліни
2 курс, осінній семестр
Семестровий
контроль/
контрольні заходи
Розклад занять
Залік / РГР
Мова викладання
Українська
Інформація про
керівника курсу/
викладачів
Лектор: проф., д.т.н., Аврутов Вадим Вікторович,
v.avrutov@kpi.ua
Розміщення курсу
4 кр. (120 год.)
Згідно з розкладом на сайті http://roz.kpi.ua/
Практичні : проф., д.т.н., Аврутов В. В.,
доц., к.т.н. Мироненко П.С., доц., д.т.н. Тягур В.М.
https://do.ipo.kpi.ua/user/view.php?id=27527&course=4822
2

3.

Перелік літератури
1. Аврутов В.В. Iнформаційні ресурси (елементи) системи
дистанційного
навчання.
Презентації
лекцій:
https://do.ipo.kpi.ua/user/view.php?id=27527&course=4822
2. Павловський М.А. Теоретична механіка. – К.: Техніка, 2002. -510 с.
3. Мещерский И.В. Сборник задач по теоретической механике. - М.:
Наука, 1986.- 448 с.
3

4.

Михайло Антонович Павловський (13.03.1942 - 2004) –
доктор технічних та економічних наук, тричі лауреат
Державних премій, заслужений діяч науки і техніки
України, нагороджений орденом „Знак пошани” та
Грамотою Верховної ради України, фахівець в галузі
механіки гіроскопів і навігаційних пристроїв, дослідженні
нелінійних просторових коливань складних конструкцій.
Народився 13 березня 1942р. в с. Ружична Хмельницької
обл., 1963р. – закінчив КПІ з відзнакою, 1963-66рр. –
аспірант кафедри „Гіроскопічні прилади і пристрої”,
1968р. – доцент тієї ж кафедри, 1977р. – зав. кафедрою
теоретичної механіки, 1985р. – створив і очолив СКБ
„Ритм”, 1993р. – один з засновників і декан факультету
авіаційних і космічних систем, 1994-2004рр. – нар. деп.
України ІІ, ІІІ, ІV скликань.
Інститут аерокосмічних технологій
корп.28, вул. Боткіна, 1,
4

5.

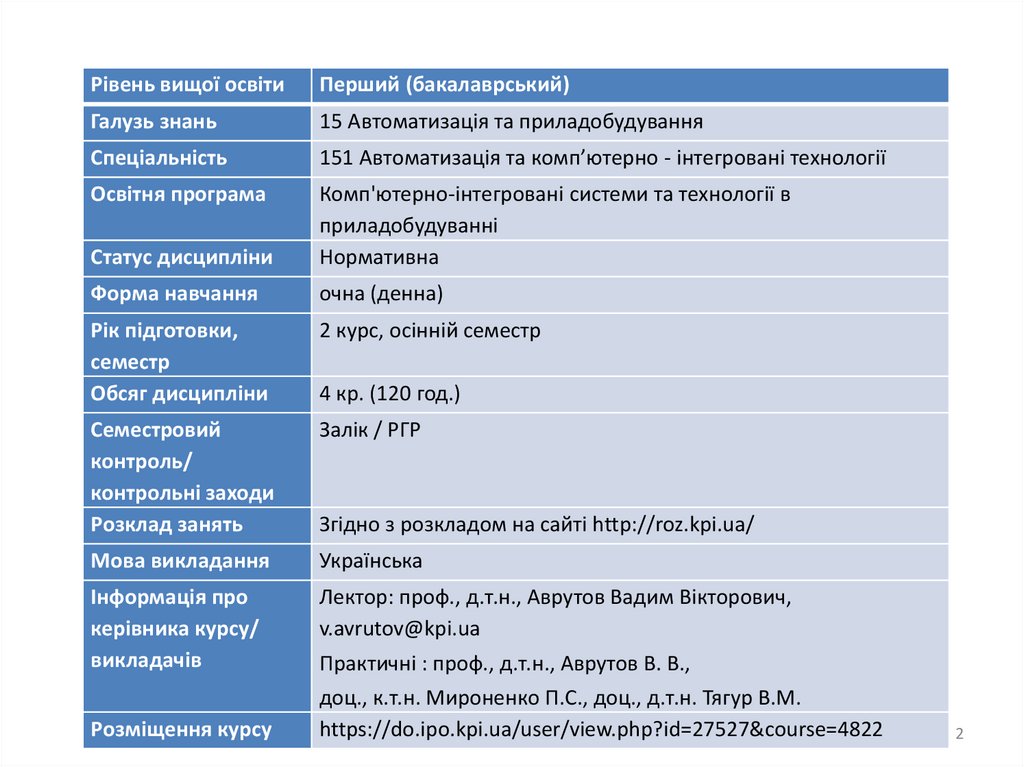
найпростіші механізми
похила площина
5

6.

колесо
6

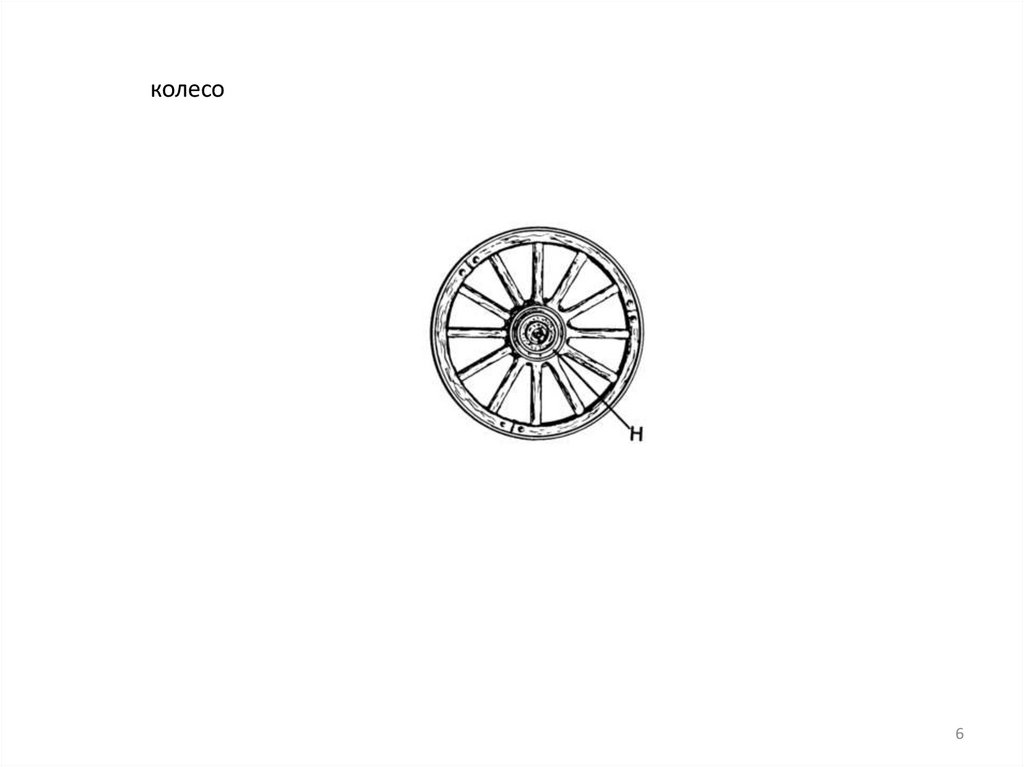
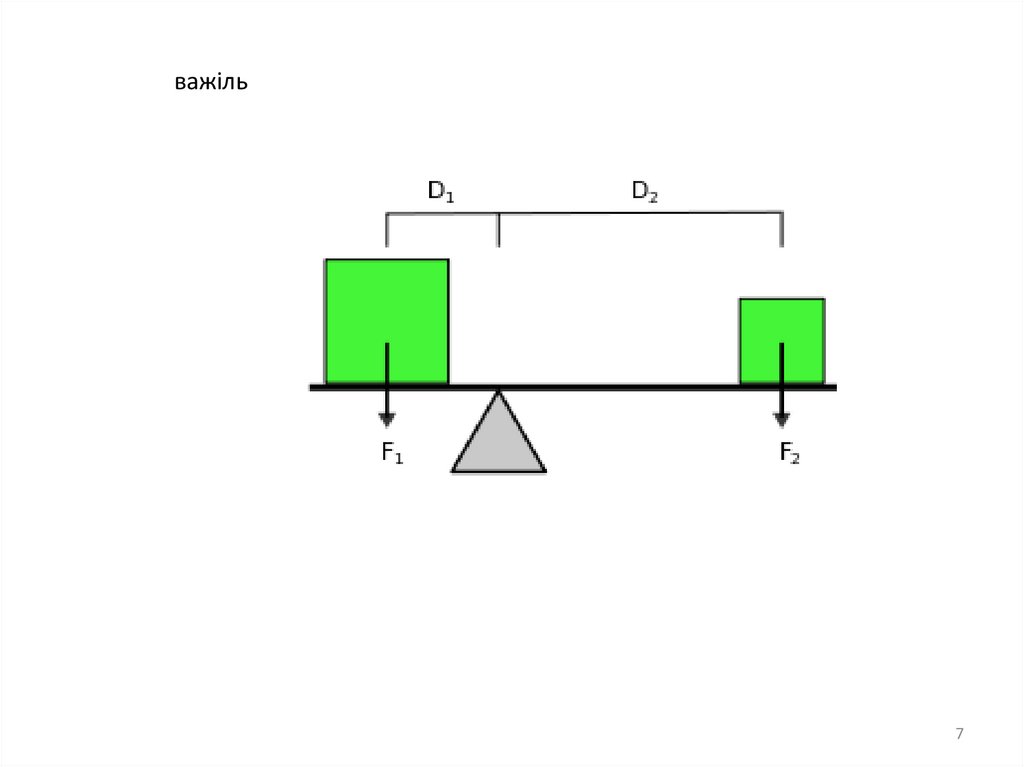
7.

важіль
7

8.

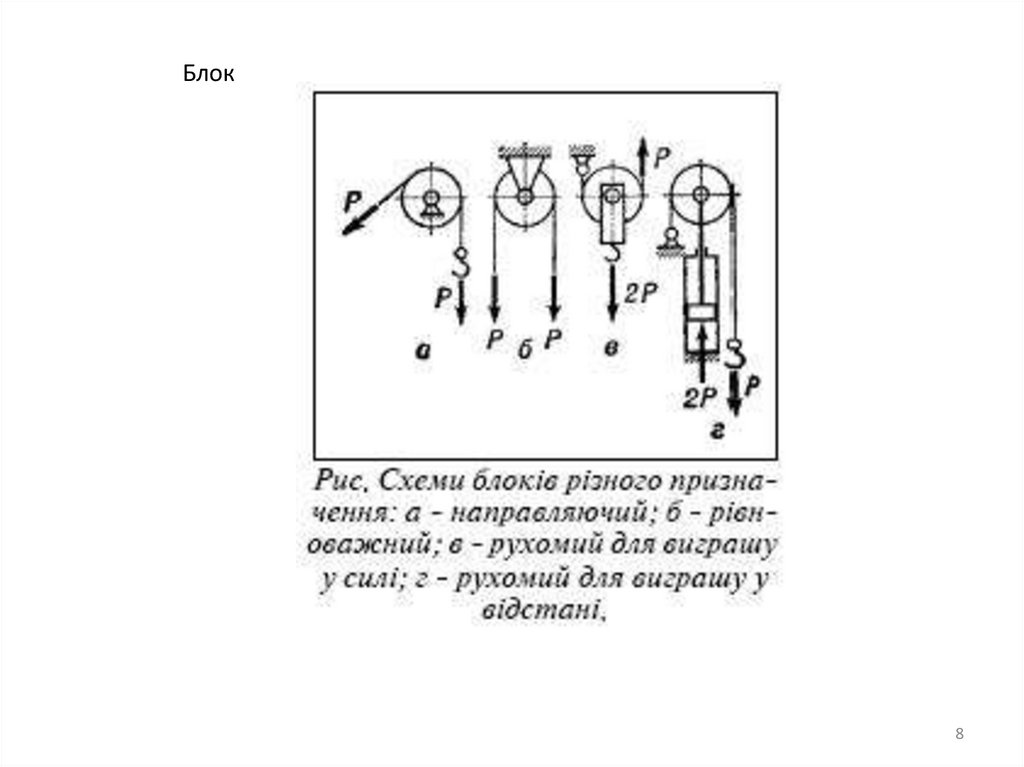
Блок
8

9.

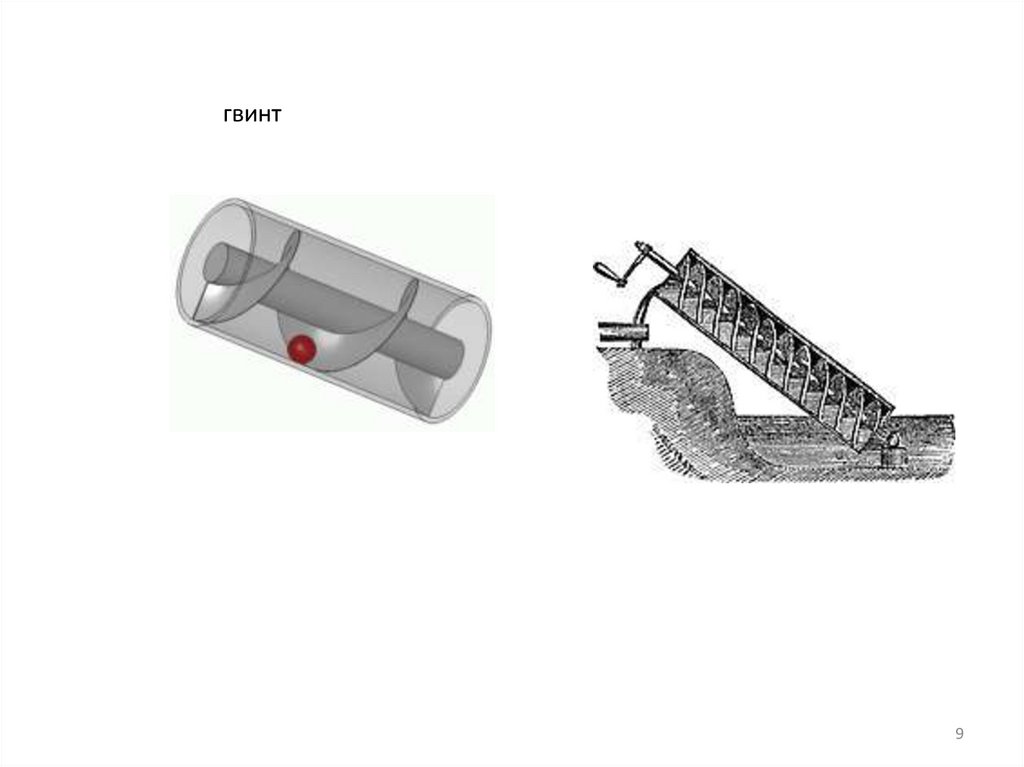
гвинт
9

10.

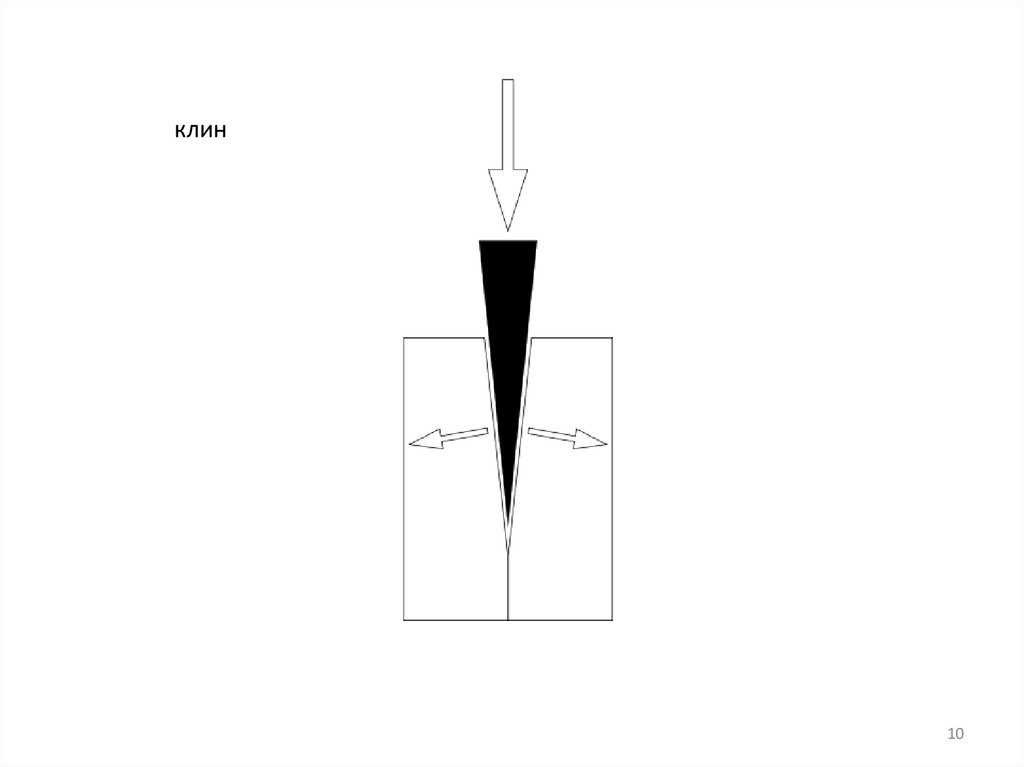
клин
10

11.

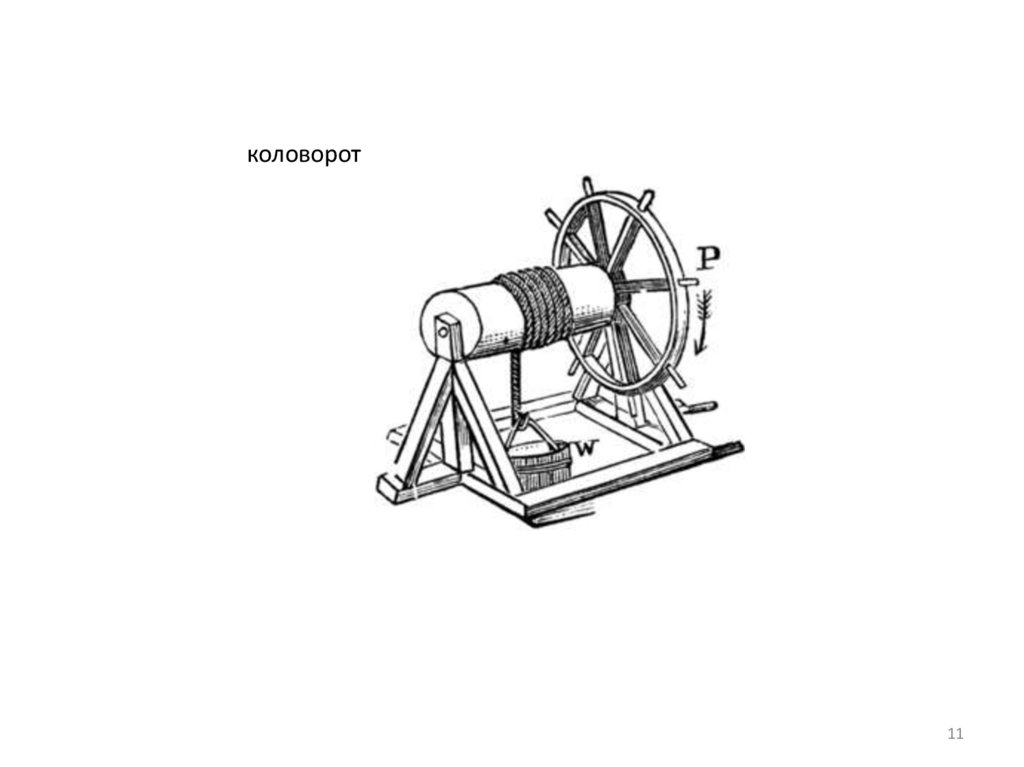
коловорот
11

12.

Архіме́д: 287—212 р. до Р.Х.
давньогрецький математик,
фізик, інженер,винахідник та астроном
«Архімед», Доменіко Фетті, 1620
12

13.

Декарт
René Descartes (1596-1650)
Ньютон
Isaac Newton (1642-1727)
[aɪzək ˈnjuːtən]

14.

Теоретична механіка розглядає не реальні матеріальні об'єкти, а їхні моделі:
• матеріальні точки
• системи матеріальних точок
• абсолютно тверді тіла.
Матеріальною точкою називається тіло кінцевої маси, розмірами якого
можна знехтувати.
Системою матеріальних точок називається сукупність точок,
положення і рух яких взаємопов'язані між собою.
Абсолютно твердим тілом називається тіло, що складається з системи
матеріальних точок, які безперервно заповнюють деяку частину простору
так, що відстань між будь-якими двома його точками залишається
незмінним.
Теор. мех.
Кінематика
Статика
Динаміка
Аналіт. механіка
14

15.

Розділ I. Кінематика
Рух точки можна визначити трьома способами:
• векторним
• координатним
• натуральним.
Векторний спосіб.
r r (t )
15

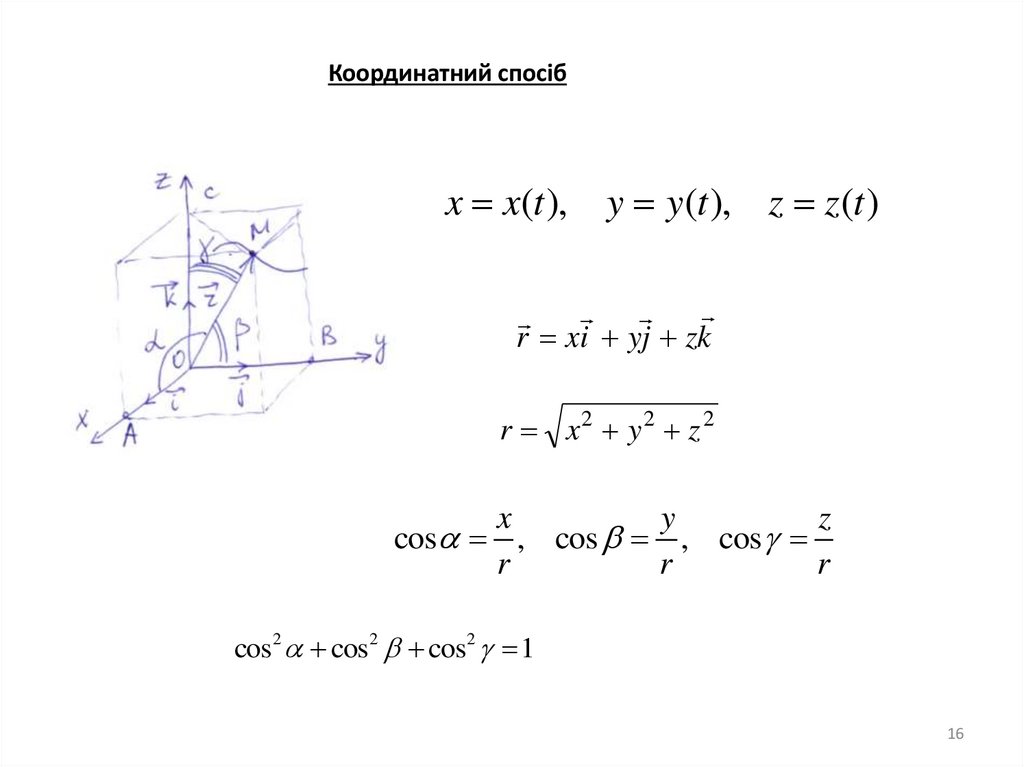
16.

Координатний спосіб
x x(t ), y y(t ), z z (t )
r xi yj zk
r x2 y2 z 2
x
y
z
cos , cos , cos
r
r
r
cos2 cos2 cos2 1
16

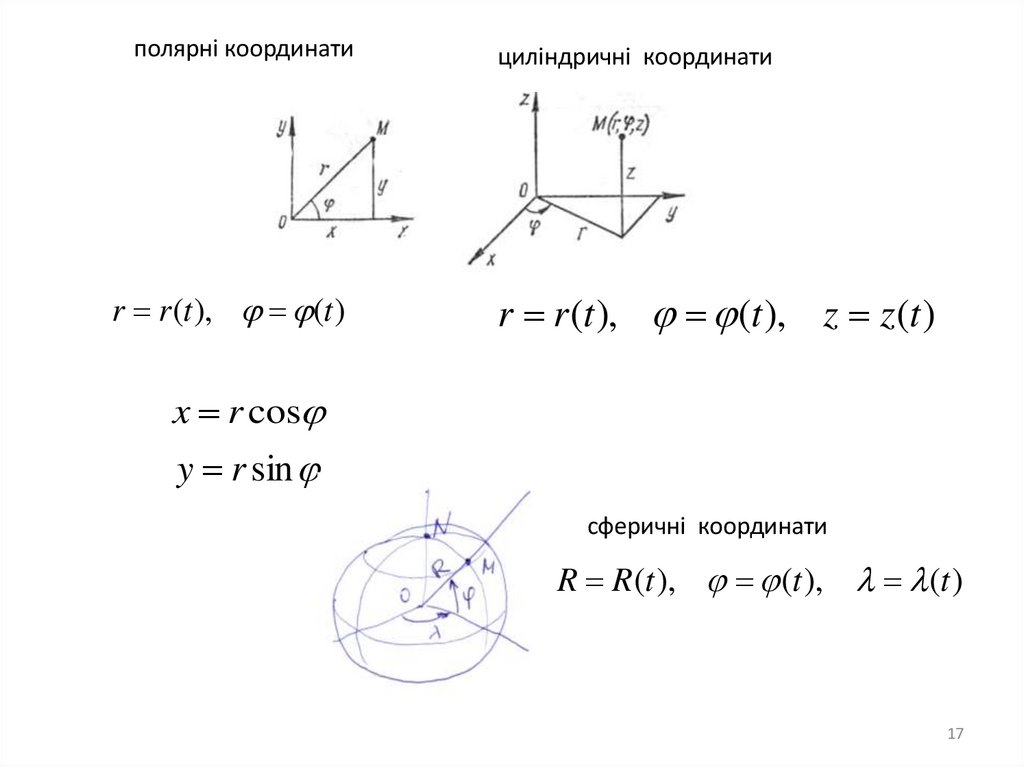
17.

полярні координати
r r (t ), (t )
циліндричні координати
r r (t ), (t ), z z (t )
x r cos
y r sin
сферичні координати
R R(t ), (t ), (t )
17

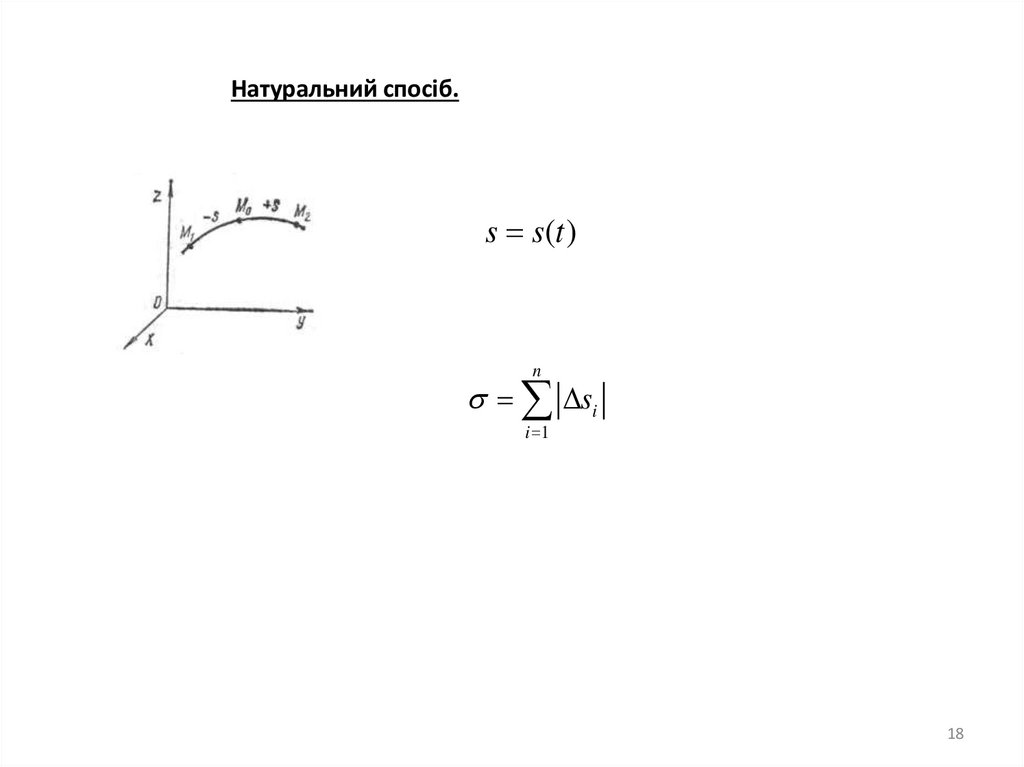
18.

Натуральний спосіб.
s s(t )
n
si
i 1
18

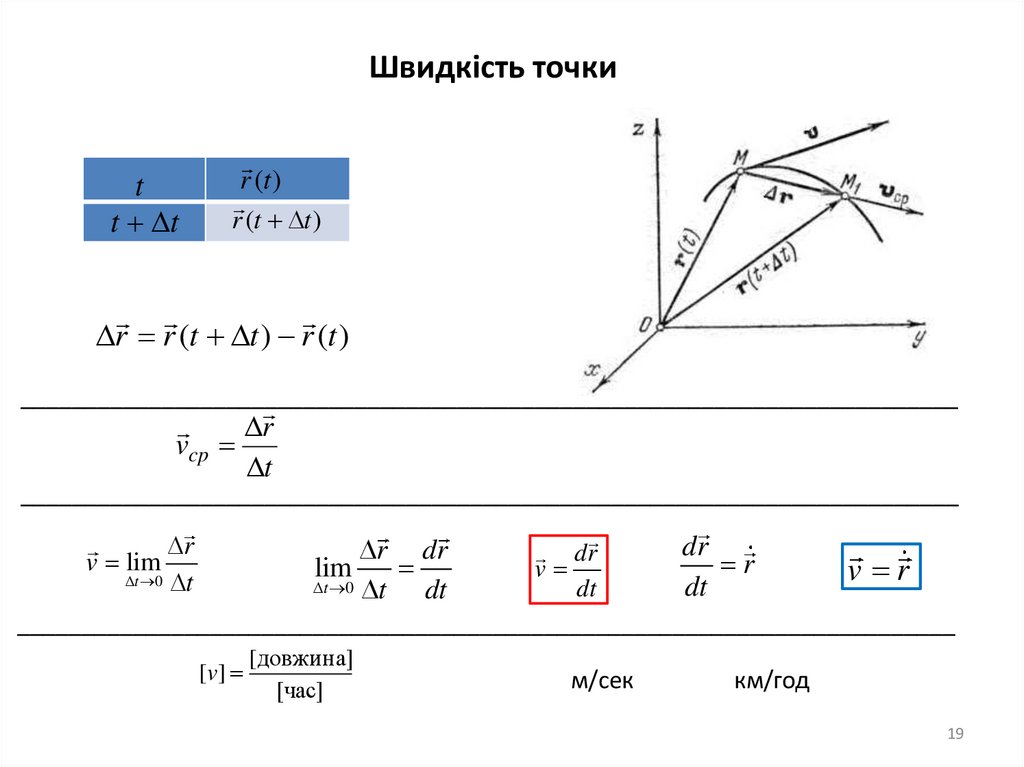
19.

Швидкість точки
t
t t
r (t )
r (t t )
r r (t t ) r (t )
_________________________________________________________________________
r
vcp
t
_________________________________________________________________________
r
t 0 t
r dr
lim
t 0 t
dt
dr
dr
r
v
v r
dt
dt
_________________________________________________________________________
v lim
[v ]
[довжина]
[час]
м/сек
км/год
19

20.

Швидкість точки при координатному способі завдання руху
x x(t ),
y y(t ), z z (t )
r xi yj zk
_________________________________________________________________________
dr
v
r x i y j z k
dt
v x x
v y y
v z z
v vxi v y j vz k
_________________________________________________________________________
v x y z
2
2
v v x2 v 2y v z2
2
_________________________________________________________________________
v
cos x, v x
v
vy
cos y, v
v
v
cos z, v z
v
20

21.

Швидкість точки в полярних координатах
x r cos
x r cos r sin
y r sin
y r sin r cos
_________________________________________________________________________
vr r
v p r
_________________________________________________________________________
v x vr cos v p sin
v y vr sin v p cos
_________________________________________________________________________
v x 2 y 2 r 2 r 2 2
21

22.

Швидкість точки при натуральному способі завдання руху
r r ( s) r s(t )
_________________________________________________________________________
r
v lim
t 0 t
r s lim r lim s
lim
t 0
t 0 s t
s t 0 t
r dr
lim
t 0 s
ds
s
lim
s
t 0 t
v s
s v
v v
v v
v v
v v
22

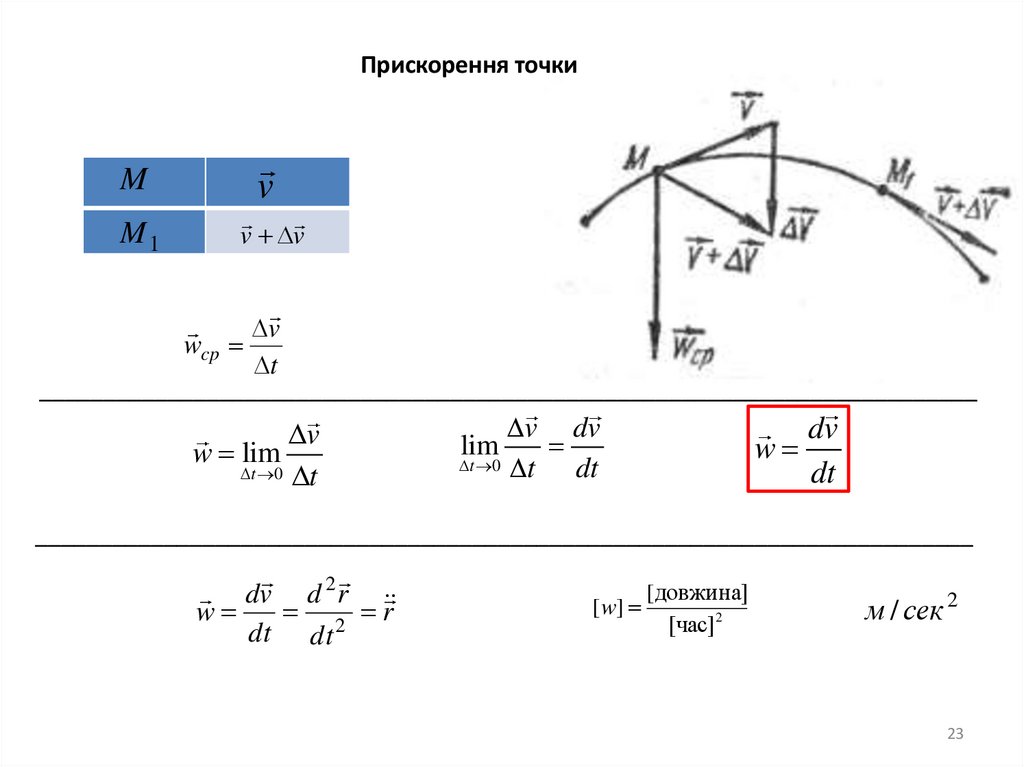
23.

Прискорення точки
M
v
M1
v v
v
wcp
t
_________________________________________________________________________
v
w lim
t 0 t
v dv
t 0 t
dt
w
lim
dv
dt
_________________________________________________________________________
dv d 2 r
w
2 r
dt dt
[ w]
[довжина]
[час]2
м / сек 2
23

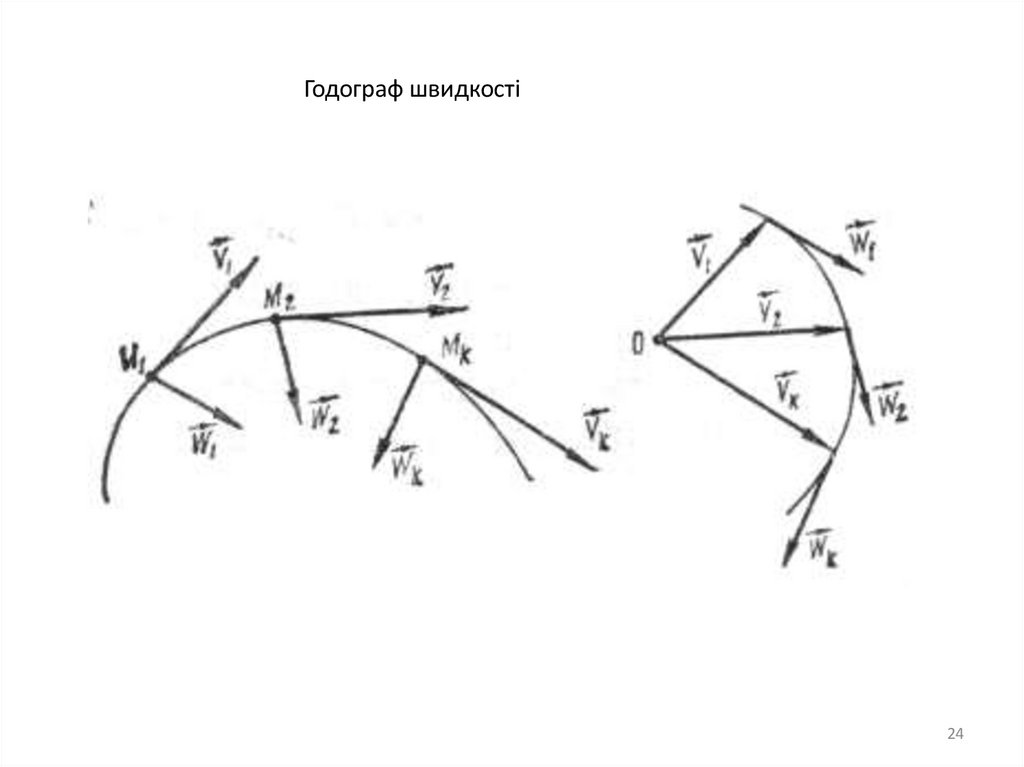
24.

Годограф швидкості
24

25.

Прискорення при координатному способі завдання руху
r xi yj zk
v vxi v y j vz k
_________________________________________________________________________
dv dvx dv y dvz
w
i
j
k
dt
dt
dt
dt
w wx i w y j wz k
_________________________________________________________________________
wx
dv y
dvx
dv
v x x , w y
v y y , wz z v z z
dt
dt
dt
_________________________________________________________________________
wx2 w 2y wz2
w
cos x, w x
w
w x 2 y 2 z 2
wy
cos y, w
w
w
w
cos z, w z
w
25

26.

Прискорення в полярних координатах
x r cos
x r cos r sin
y r sin
y r sin r cos
_________________________________________________________________________
x r cos r sin r sin r sin r 2 cos
r r 2 cos r 2r sin .
y r sin r cos r cos r cos r 2 sin
r r 2 sin r 2r cos .
_________________________________________________________________________
wr r r 2 , w p r 2r .
wx wr cos w p cos wr cos w p sin ,
2
w y wr cos w p cos wr sin w p cos .
2
________________________________________________
wx x , wy y
26

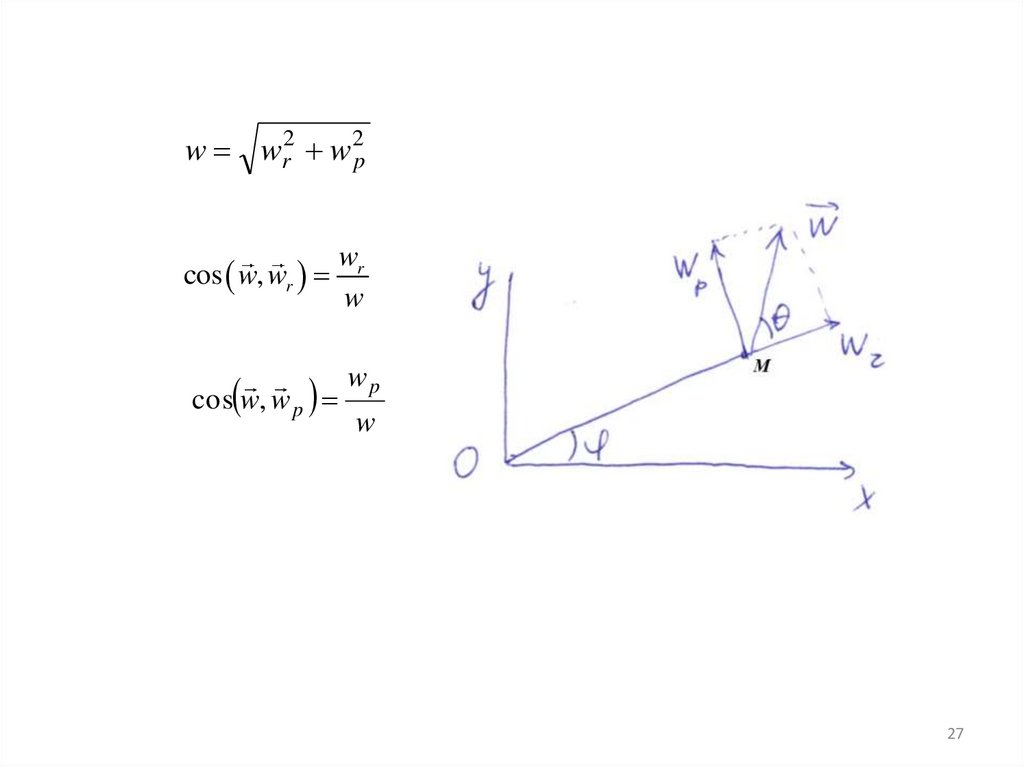
27.

w wr2 w 2p
wr
cos w, wr
w
wp
cos w, w p
w
27