Похожие презентации:
Невизначений інтеграл
1.
2. §1. НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
Глава 7Інтегральне числення функції
однієї змінної
§1. НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
• 1.4. Поняття про комплексні числа
Озн. Комплексним числом називається вираз
(8)
z a bi,
де а та b — дійсні числа, а символ і — уявна одиниця, яка
визначається умовою і2 = –1.
3.
z a bi,(8)
Озн. Число а називається дійсною частиною
комплексного числа z і позначається а = Re z,
a b — уявною частиною z, b = Im z
(від французьких слів: réel — дійсний,
imaginaire — уявний).
Озн. Вираз, що стоїть справа у формулі (8), називається
алгебраїчною формою запису комплексного числа.
4.
Озн. Два комплексні числаz = а bі, z = а bі,
які відрізняються лише знаком уявної частини, називаються
спряженими.
Озн. Два комплексні числа
z1 = а1 b1і і z2 = а2 b2і
вважаються рівними (z1 = z2) тоді і тільки тоді, коли рівні
їхні дійсні частини і рівні їхні уявні частини: а1 = а2, b1 = b2.
(Комплексні числа не порівнюють).
5.
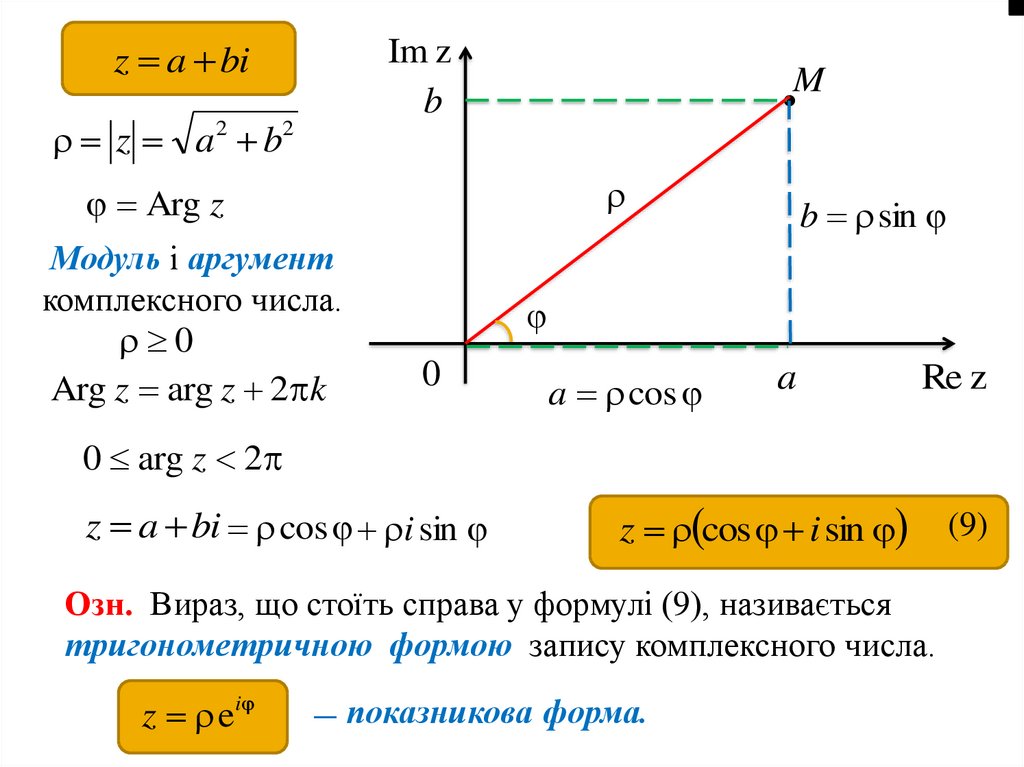
z a biIm z
b
z a 2 b2
M
Arg z
Модуль і аргумент
комплексного числа.
0
Arg z arg z 2 k
b sin
0
a cos
a
Re z
0 arg z 2
z a bi cos i sin
z cos i sin
Озн. Вираз, що стоїть справа у формулі (9), називається
тригонометричною формою запису комплексного числа.
z ei
—
показникова форма.
(9)
6.
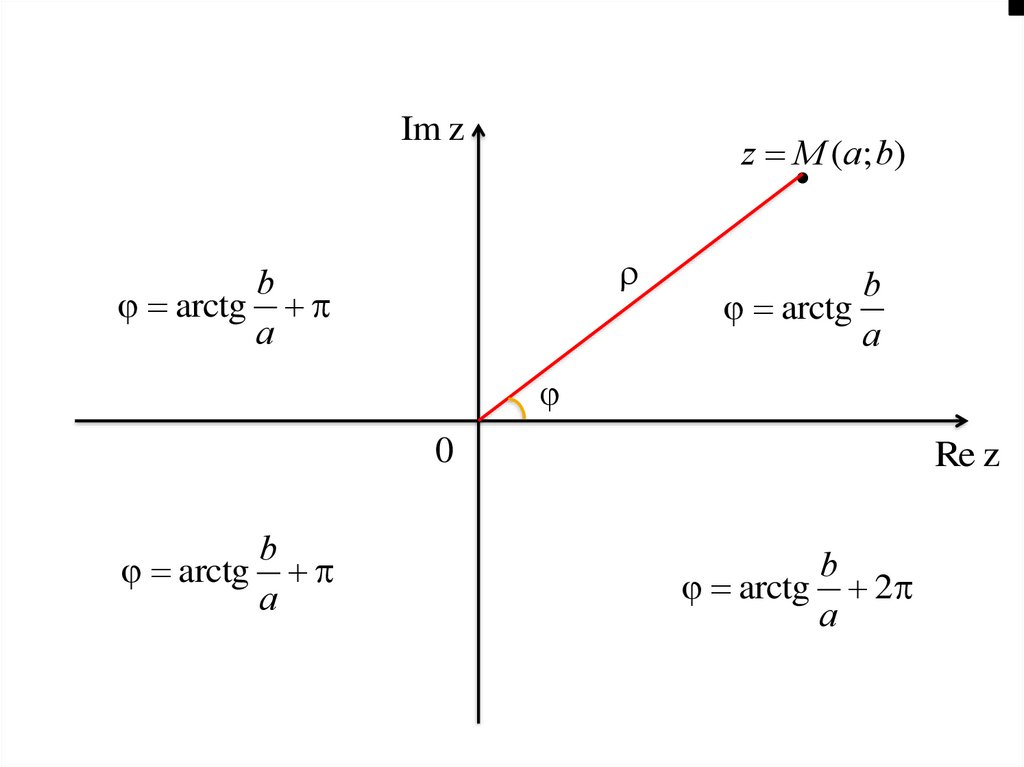
Im zz M (a; b)
b
arctg
a
b
arctg
a
0
b
arctg
a
Re z
b
arctg 2
a
7.
Дії над комплексними числамиz1 a1 b1i
z2 a2 b2i
z1 2 3i
z2 5 7i
i 2 1
z1 z2 2 3i 5 7i 2 5 3 7 i 7 4i
z1 z2 2 3i 5 7i 10 14i 15i 21i 2 31 i
2
z1 2 3i 2 3i 5 7i 10 14i 15i 21i
2
2
5 7i
z2 5 7i 5 7i 5 7i
11 29i 11 29i
11 29
i
25 49
74
74 74
8.
Дії над комплексними числамиi i
1
i 1
2
i i
i4 1
3
i 5 i
i 6 1
i 4 n 1 i
(ост. 1)
(*,25)
i 4 n 2 1
(ост. 2)
(*,50)
i 7 i
i 4 n 3 i
(ост. 3)
(*,75)
i8 1
i 4n 1
(ост. 0)
(*,00)
i138 1
138 : 4 = 34 (ост. 2)
138 : 4 = 34,5
34 4 = 136
1 i
2
2i
1 i
2
2i
9.
Дії над комплексними числамиz1 1 cos 1 i sin 1
z2 2 cos 2 i sin 2
z1 z2 1 2 cos 1 2 i sin 1 2
z1
1
cos 1 2 i sin 1 2
2
z2
z n n cos n i sin n
n
—
формула Муавра
2 k
2 k
i sin
z cos
n
n
n
k 0, 1, 2, , n 1
10.
Прикладиz1 2 cos 210 i sin 210
z2 3 cos 320 i sin 320
z1 z2 2 3 cos 210 320 i sin 210 320
6 cos 530 i sin 530 6 cos170 i sin 170
2
z1
cos 210 320 i sin 210 320
3
z2
2
2
cos 110 i sin 110 cos 250 i sin 250
3
3
11.
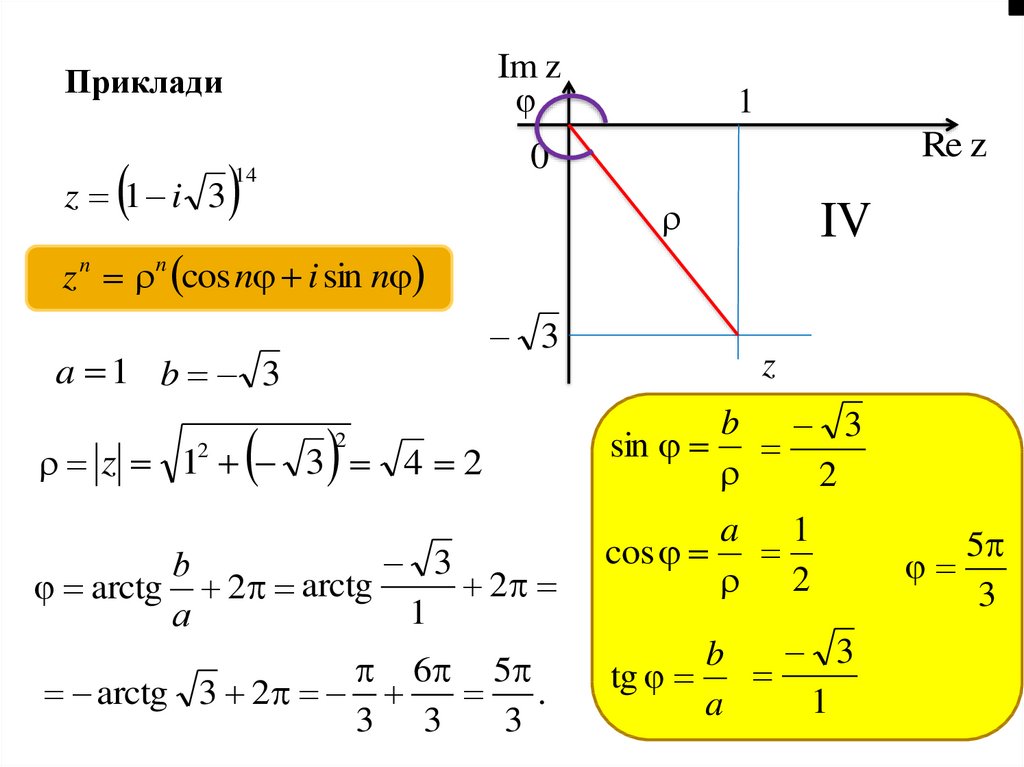
Im zПриклади
z 1 i 3
1
Re z
0
14
IV
z n n cos n i sin n
3
a 1 b 3
2
z 12 3 4 2
3
b
2
arctg 2 arctg
1
a
6 5
.
arctg 3 2
3 3
3
z
b 3
sin
2
a 1
cos
2
3
b
tg
1
a
5
3
12.
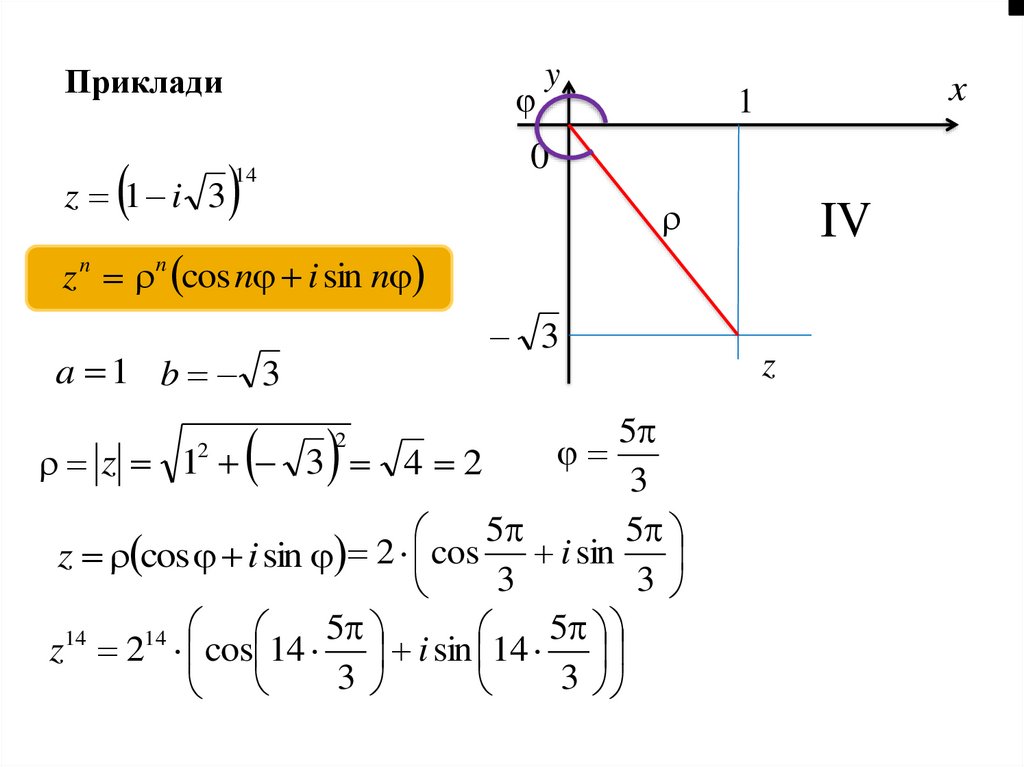
Прикладиz 1 i 3
y
x
1
0
14
IV
z n n cos n i sin n
3
a 1 b 3
5
z 1 3 4 2
3
5
5
2
cos
i
sin
z cos i sin
3
3
5
5
14
14
z 2 cos 14 i sin 14
3
3
2
2
z
13.
Прикладиz 1 i 3
14
y
x
1
0
IV
z n n cos n i sin n
a 1 b 3
3
z
5
5
z 2 cos 14 i sin 14 214 cos 70 i sin 70
3
3
3
3
14
14
70 66
70 66
2 cos
i sin
3
3
3
3
14
1
4
4
3
14
213 213i 3
2 cos
i sin
2 i
3
3
2
2
14
14.
Прикладиz 4 16
n
Z 16 16 0i
a 16
2 k
2 k
i sin
z cos
n
n
n
b 0
k 0, 1, 2, , n 1
2 k
2 k
4 16 cos
i sin
4
4
z0 2 cos i sin 2 i 2
4
4
3
3
z1 2 cos i sin
2 i 2
4
4
5
5
z2 2 cos i sin
2 i 2
4
4
7
7
i sin
z3 2 cos
2 i 2
4
4
z 4 Z 4 16
16
k 0, 3
15.
e xi cos x i sin xe xi cos x i sin x
e xi e xi
cos x
ch xi
2
cos xi ch x
e xi e xi 1
sin x
sh xi
2i
i
sin xi i sh x
16. §1. НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
Глава 7Інтегральне числення функції
однієї змінної
§1. НЕВИЗНАЧЕНИЙ ІНТЕГРАЛ
• 1.1. Поняття первісної функції та
невизначеного інтеграла
Озн. Функція F(х) називається первісною функції f (х)
на проміжку ‹а; b›, якщо F(х) диференційовна на ‹а; b› і
F′(х) = f (х), х ‹а; b›.
17.
Прикладиf ( x) x ,
2
x R
3
x
1
3
x3
F ( x)
C
3
x R
3
x
F ( x)
3
F ( x)
f ( x ) cos x,
x
F ( x ) x 2
3
3
x
F ( x ) 1 x 2
3
3
x
F ( x ) C x 2
3
3
F ( x ) sin x C
F ( x ) sin x C cos x
18.
Теорема. Якщо F(х) — первісна функції f (х) на проміжку ‹а; b›,то всяка інша первісна функції f (х) на цьому самому проміжку
має вигляд F(х) + С.
Озн. Якщо F(х) — первісна функції f (х) на проміжку
‹а; b› і С — довільна стала, то вираз F(х) + С називається
невизначеним інтегралом функції f (х) на цьому проміжку
і позначається символом
f ( x)dx.
— інтеграл
f ( x )dx — підінтегральний вираз
f ( x)
— підінтегральна функція
19.
Властивості1°. Похідна від невизначеного інтеграла дорівнює
підінтегральній функції:
f ( x)dx f ( x)
2°. Невизначений інтеграл від диференціала деякої функції
дорівнює сумі цієї функції і довільної сталої:
dF ( x) F ( x) C
20.
Властивості3°. Диференціал від невизначеного інтеграла дорівнює
підінтегральному виразу:
d
f ( x)dx f ( x)dx
4°. Сталий множник можна виносити за знак інтеграла:
Cf ( x)dx C f ( x)dx
21.
Властивості5°. Невизначений інтеграл від алгебраїчної суми двох функцій
дорівнює алгебраїчній сумі інтегралів від цих функцій:
f ( x) g ( x) dx f ( x)dx g ( x)dx
6°. Якщо
і
f ( x)dx F ( x) C
u ( x ) — довільна функція, що має неперервну похідну, то
f (u)du F (u) C
22.
3x
2
x
dx 3 C
3
u
2
u
du 3 C
3
sin
x
2
2
sin
x
d
sin
x
sin
x
cos
xdx
C
3
3
dx
tg
x
2
2
tg x d tg x tg x cos2 x 3 C
3
dx
ln
x
2
2
ln
x
d
ln
x
ln
x
C
x
3
u u(x )
23.
• 1.2. Таблиця основних інтегралів1
u
u
C 1
1 du
1
du
ln u C
2
u
au
u
C
3 a du
ln a
4
5
e
u
du e C
u
sin u du cos u C
9
ch u du sh u C
tg u du ln cos u C
10
ctg u du ln sin u C
8
11
12
6
sh u du ch u C
13
7
cos u du sin u C
14
du
cos2 u tg u C
du
ch 2 u th u C
du
sin 2 u ctg u C
du
sh 2 u cth u C
24.
• 1.2. Таблиця основних інтегралів15
du
u
sin u ln tg 2 C
du
u
ln tg C
16
cos u
4 2
17
18
du
u
arcsin C
a
a2 u2
du
u2 A
ln u u 2 A C
25.
• 1.2. Таблиця основних інтегралів19
du
1
u
a 2 u 2 a arctg a C
20
du
1
u a
u 2 a 2 2a ln u a C
21
22
2
u
a
u
a 2 u 2 du
a 2 u 2 arcsin C
2
2
a
u 2
A
u Adu
u A ln u u 2 A C
2
2
2
26.
• 1.3. Основні методи інтегрування1°. Метод безпосереднього інтегрування.
1
1
3
3
2
2
x
x
dx
2
xdx
x
dx
3
x
dx
3
x
1 1
2
x 3
x
x
2 C1
C2 3
C3
1 1
2
1 1
2
3
1
1
2
2
93 2
2
93 2
2
x x x
x 2C1 C2 3C3 x x x
x C
3
2
3
2
2
27.
2x
x
x
x
2x
2 x
cos
sin
dx
cos 2 cos sin sin dx
2
2
2
2
2
2
1 sin x dx
dx sin xdx
x cos x C
1
1
ctg xdx sin 2 x 1 dx sin 2 x dx dx ctg x x C
2
dx
dx
dx
sin 2 x cos2 x
sin 2 x cos2 x sin 2 x cos2 x dx cos2 x sin 2 x
tg x ctg x C
28.
2°. Метод підстановки (заміни змінної).Теорема. Нехай F(х) — первісна функції f (х) на проміжку ‹а; b›,
тобто
f x dx F x C
x a;b
і нехай функція x = φ(t) визначена і диференційовна на проміжку
‹α; β›, причому множина значень цієї функції є проміжок ‹а; b›.
Тоді справедлива формула
f t t dt F t C
t ; .
29.
g x dxt x
f x x dx =
dt x dx
F t C F x C.
x t
1
g
x
dx
t
( x)
dx t dt
g t t dt
G t C G 1 x C.
f t dt
30.
t 2 ln x 31 4
1 3
2 ln x 3 dx
t
C
t
dt
2
x
8
2
dt dx
x
3
1
4
2 ln x 3 C
8
3
1
3 5ctg x
1
3
dx
3
5
ctg
x
d 3 5ctg x
2
sin x
5
4
3
3 5ctg x 3 C
20
t 3 5 ctg x
5
dt 2 dx
sin x
31.
t x 1x
dx dt dx
x 1
x t 1
3
3
2
t
3
t
3t 1
t 1 dt
dt
t
t
3
1
t3 3 2
2
t 3t 3 dt
t 3t ln t C
t
3 2
3
x 1 3
2
x 1 3 x 1 ln x 1 C
3
2
32.
x sin t1 x 2 dx dx cos tdt
t arcsin x
1 sin 2t cos tdt
2
cos
tdt
1
1 sin 2t
1
2
t
sin
t
1
sin
t C
t
C
1 cos 2t dt
2
2
2
2
1
1
arcsin x x 1 x 2 C
2
2
33.
t xdx
2
t
x
2 x
2tdt dx
2tdt
2 t 2
2 t 2 2 t dt
2 t 2
2
2
dt
2 1
dt 2 t 2 ln 2 t
2 t 2 t
2 t
2 x 4 ln 2 x C
34.
3°. Метод інтегрування частинами.u u x
v v x
d uv udv vdu
udv d uv vdu
udv d uv vdu
udv uv vdu
(6)
Формула (6) називається формулою інтегрування частинами.
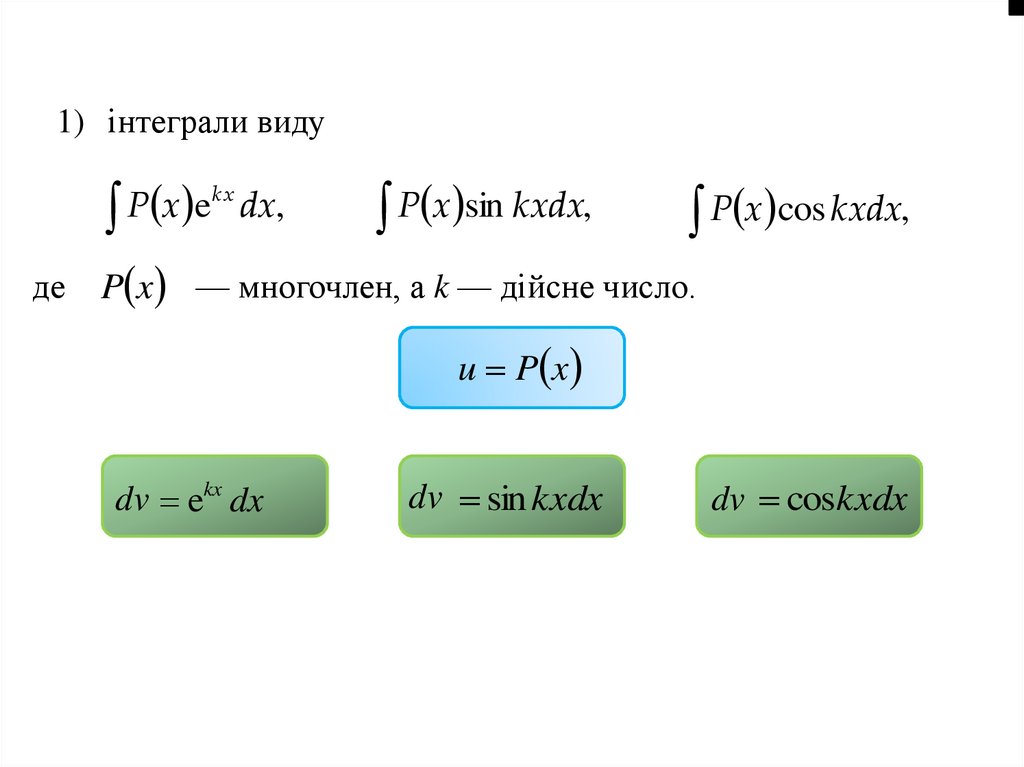
35.
1) інтеграли видуkx
P
x
e
dx,
де
P x sin kxdx,
P x cos kxdx,
P x — многочлен, a k — дійсне число.
u P x
dv ekx dx
dv sin kxdx
dv coskxdx
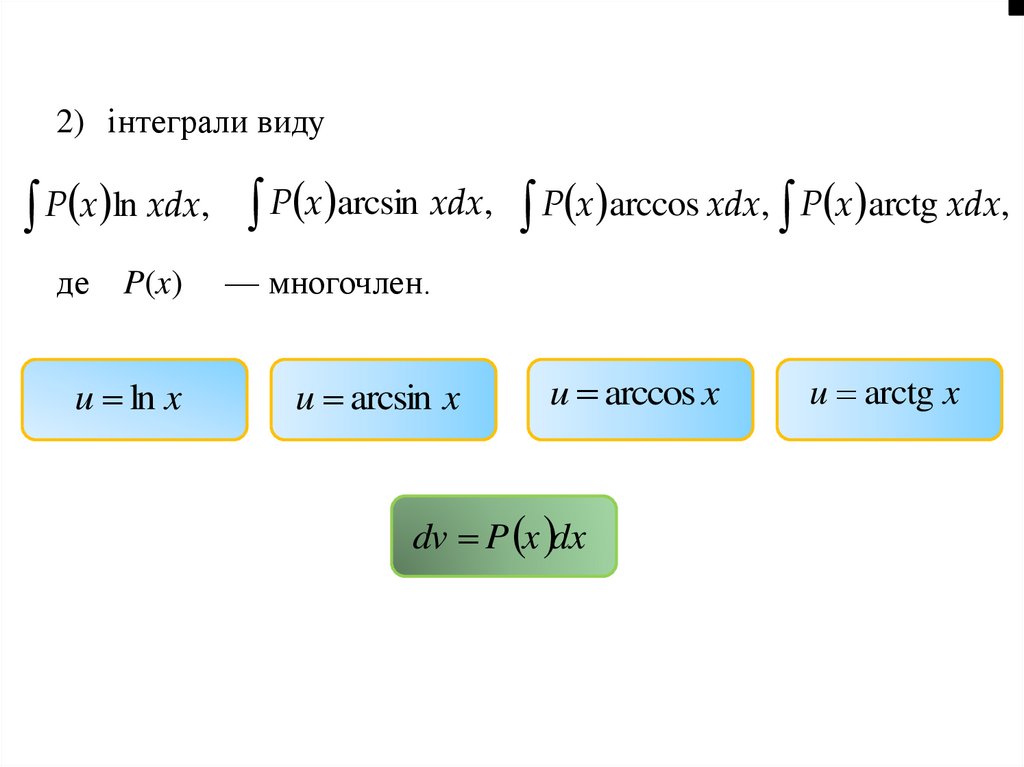
36.
2) інтеграли видуP x ln xdx, P x arcsin xdx, P x arccos xdx, P x arctg xdx,
де
P(x)
u ln x
— многочлен.
u arcsin x
u arccos x
dv P x dx
u arctg x
37.
3) інтеграли видуx
e
sin xdx,
x
e
cos xdx,
u e x
dv sin xdx
dv cos xdx
u cos x
u sin x
dv e x dx
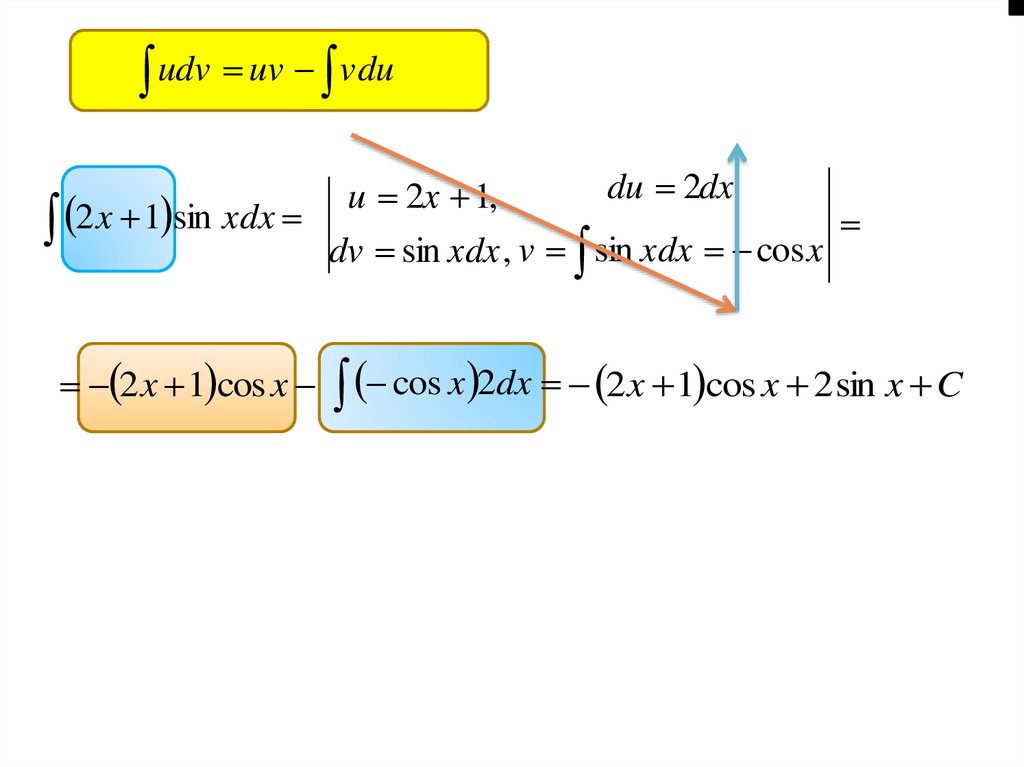
38.
udv uv vdu2 x 1 sin xdx
2 x 1 cos x
u 2x 1,
du 2dx
dv sin xdx , v sin xdx cos x
cos x 2dx 2x 1 cos x 2 sin x C
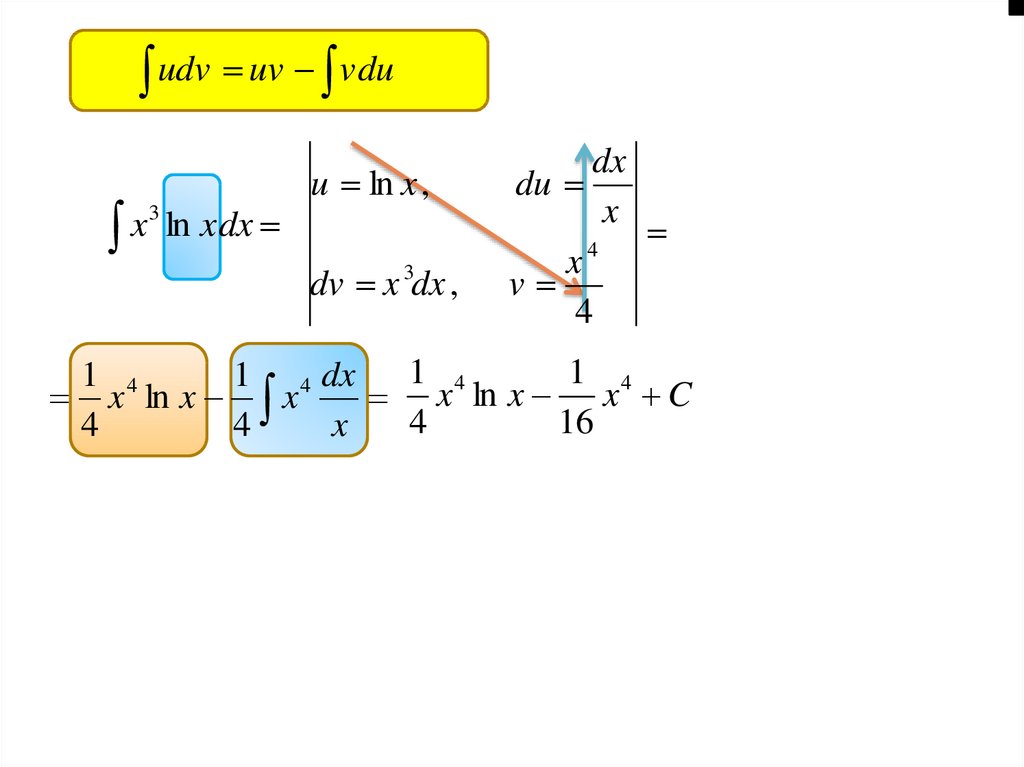
39.
udv uv vdu3
x
ln xdx
u ln x ,
dv x 3dx ,
dx
du
x
4
x
v
4
1 4
1 4
1 4 dx 1 4
x ln x x
x ln x x C
4
16
4
4
x
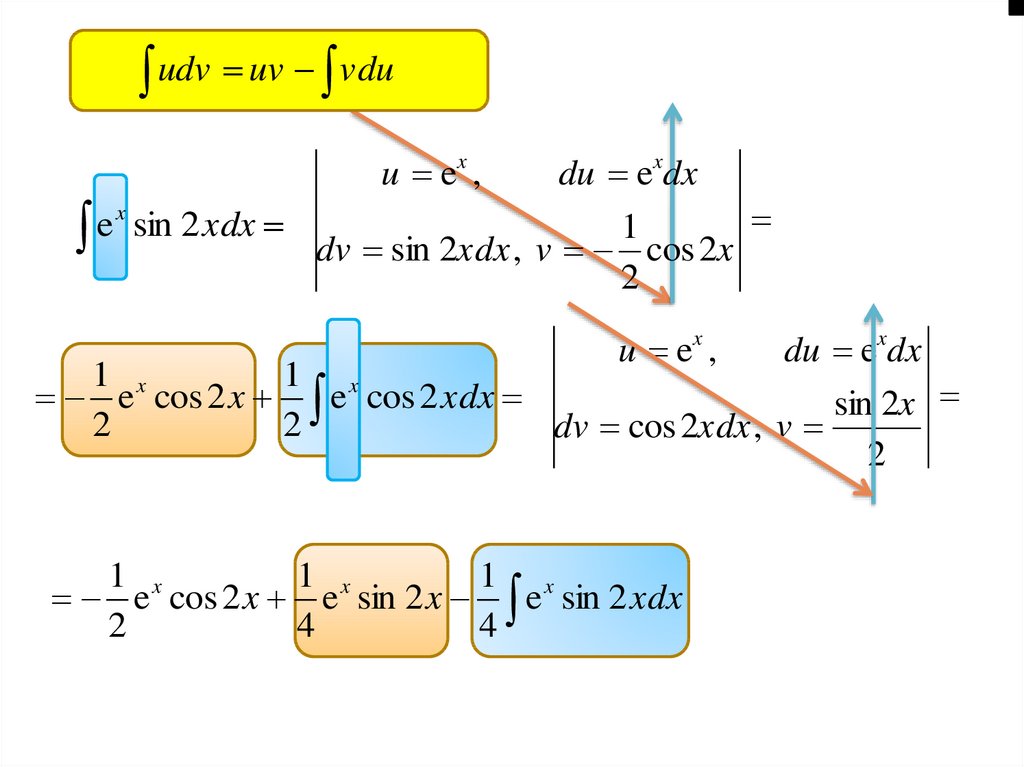
40.
udv uv vduu ex ,
x
e
sin 2 xdx
du exdx
1
dv sin 2xdx , v cos 2x
2
u ex ,
du exdx
1 x
1 x
e cos 2 x e cos 2 xdx
sin 2x
2
2
dv cos 2xdx , v
2
1
1
1
e x cos 2 x e x sin 2 x e x sin 2 xdx
2
4
4
41.
1 x1 x
1 x
e sin 2 xdx 2 e cos 2 x 4 e sin 2 x 4 e sin 2 xdx
x
1 x
1 x
1
I e cos 2 x e sin 2 x I
2
4
4
1
1 x
1 x
I I e cos 2 x e sin 2 x
4
2
4
5
1 x
1 x
I e sin 2 x e cos 2 x
4
4
2
4e x 1
1
I
sin 2 x cos 2 x
5 4
2
x
e
x
e sin 2 xdx 5 sin 2 x 2 cos 2 x C
42.
• 1.5. Деякі відомості про раціональні функціїОзн. Многочленом (поліномом або цілою
раціональною функцією) називається функція:
Pn ( x ) a0 x n a1 x n 1 ... an .
(13)
Теорема 1. (теорема Безу). Остача від ділення многочлена
на різницю (x – a) дорівнює Pn a .
Теорема 2. (основна теорема алгебри). Всякий многочлен
степеня n > 0 має хоча б один корінь, дійсний або
комплексний.
43.
Теорема 3. Всякий многочлен n-го степеня можна подати увигляді
Pn x a0 x x1 x x2 ... x xn .
(17)
Озн. Вираз (17) називається розкладом многочлена на
лінійні множники.
x3 x 2 9 x 9 x 1 x 3i x 3i
Приклад.
5x 4 40 x 3 115x 2 140 x 60 5 x 1 x 2 x 3 x 4 .
Pn x a0 x x1 ... x xm x p1x q1 ... x ps x qs
k1
km
2
l1
2
ls
(19)
44.
Озн. Відношення двох многочленів називаєтьсяраціональною функцією або раціональним дробом.
Pm x
Qn x
P x 0, Q x 0 .
m
Раціональний дріб правильний,
якщо m < n
Раціональний дріб неправильний, якщо m n
Pp x
Pm x
Wk ( x)
Qn x
Qn x
n
45.
Теорема 4. Нехай знаменник правильного раціональногодробу розкладено на множники за формулою (19):
Pn x a0 x x1 ... x xm x p1x q1 ... x ps x qs
k1
km
2
l1
2
ls
(19)
46.
Теорема 4. Нехай знаменник правильного раціональногодробу розкладено на множники за формулою (19):
Qn x a0 x a ... x b x px q ... x lx s ,
2
2
тоді цей дріб можна подати у вигляді
Pp x
A
A2
A1
...
...
2
x a
Qn x x a x a
(21)
B
B2
B1
...
...
2
x b
x b
x b
M x N
L x F
M1 x N1
L1 x F1
.
... 2
2
... 2
2
x px q
x lx s
x px q x lx s
Озн. Вираз (21) називається розкладом правильного
раціонального дробу на елементарні дроби.
47.
x 4 2 x 3 5x 2 1Приклад 1.
x x 1
2
2
A Bx C Dx E
2
2
2
x x 1
x 1
x 2 x 5 x 1 A x 1 Bx C x 2 1 x Dx E x
4
3
2
2
2
A B x 4 Cx3 2 A B D x 2 C E x A
A B 1
C 2
2 A B D 5
C E 0
A 1
x 4 2 x 3 5x 2 1
x x 1
2
2
A 1
B 2
C 2
D 5
E 2
1 2x 2
5x 2
2
2
2
x
x 1
x 1
48.
Приклад 2.2x 1
A
B
C
x( x 1)( x 2)
x x 1 x 2
2x 1 A( x 1)( x 2) Bx ( x 2) Cx( x 1).
x 0,
x 1,
x 2,
1 A( 1) ( 2),
1
A ;
2
1 B,
B 1;
3 2C
3
C .
2
2x 1
1
1
3
.
x( x 1)( x 2)
2 x x 1 2( x 2)
49.
• 1.6. Інтегрування раціональних функційPp x
Pm x
Qn x dx Wk ( x)dx Q x dx
n
A
1
x a dx A x a d ( x a ) Aln x a C.
A
A
x a n dx (1 n)( x a)n 1 C.
p
Mx N
x t
dx
2
x 2 px q
dx dt
50.
Приклад.x t 2
2 t 2 3
2x 3
dx dx dt
dt
2
2
x 4x 9
t 2 4 t 2 9
t x 2
2t 1
2
dt
t 5
2t
t 2 5 dt
1
t 2 5 dt
1
t
arctg
C
ln t 5
5
5
2
1
x 2
arctg
C.
ln x 4 x 9
5
5
2
51.
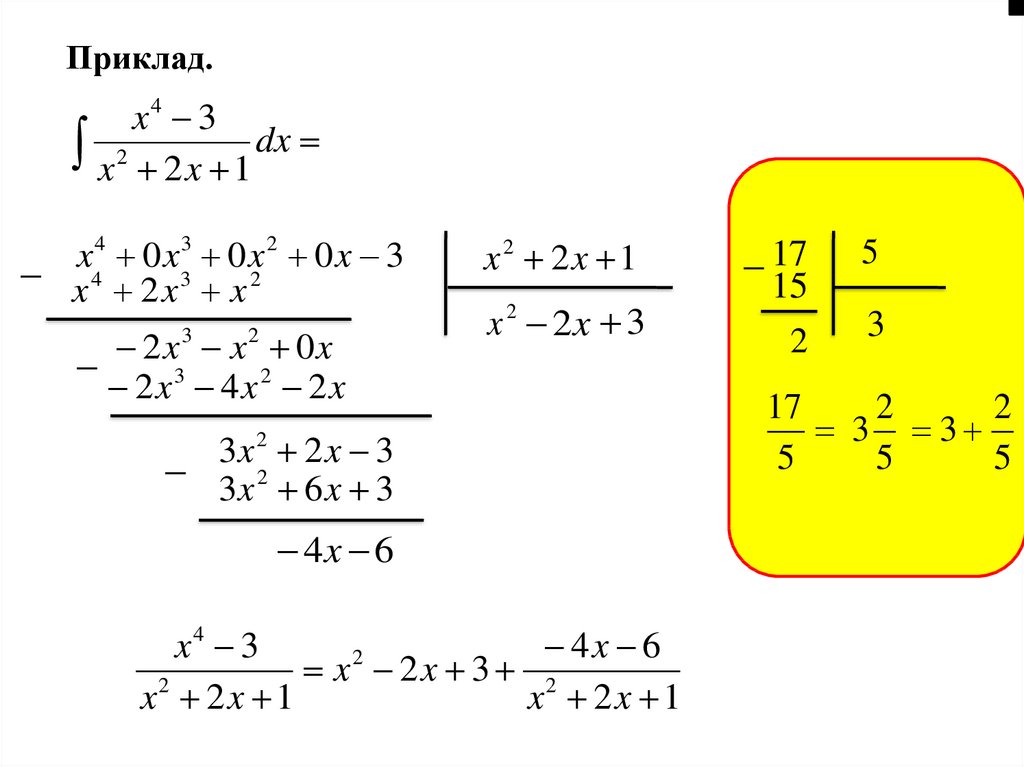
Приклад.x4 3
x 2 2 x 1 dx
x4 0x3 0x2 0x 3
x 4 2x3 x 2
2x x 0x
3
2
2x3 4x2 2x
x2 2x 1
x 2 2x 3
3x 2 2 x 3
3x 2 6 x 3
4x 6
x4 3
4x 6
2
x 2x 3 2
2
x 2x 1
x 2x 1
17
15
5
2
3
17
2
2
3 3
5
5
5
52.
Приклад.x4 3
x 2 2 x 1 dx
4x 6
x 2 x 3 dx x 2 2 x 1dx
x t 1
3
p
x
2
x
3
x t
x 2 3x 2 2
dx dx dt
2
3
x 2x 1
dx dt
t x 1
2
x3
2 t 1 3
2
x 3x 2
dt
2
3
t 1 2 t 1 1
x3
2t 1
2
x 3x 2 2 dt
3
t
x3
1
2
2
x 3x 2 dt 2 dt
3
t
t
3
x
2
x3
1
2
2
C.
x 3x 2 2 ln t C x 3x 4 ln x 1
3
x 1
3
t
53.
• 1.7. Інтегрування деяких ірраціональних ітрансцендентних функцій
3u 2v 1
R (u , v )
u 2 3v 2
2
u u (x ) v v (x )
u x 1 v 3 x
1°. Інтеграли виду
m
r
n
s
ax b
ax b
R x, cx d , , cx d dx
ax b k
t k HCK (n, s )
cx d
k LСM(n, s)
54.
Приклад.3
dx
x x
x t6
5
3
6
t
dt
t
dt
5
1 1 dx 6t dt t 2 t 3 6 t 1
x3 x2
t 6 x
dx
t3 1 1
t 1 t 2 t 1 1
6
dt 6
dt
t 1
t 1
a 3 b3 a b a 2 ab b2
t 3 1 t 1 t 2 t 1
55.
Приклад.3
dx
x x
x t6
5
3
6
t
dt
t
dt
5
1 1 dx 6t dt t 2 t 3 6 t 1
x3 x2
t 6 x
dx
t3 1 1
t 1 t 2 t 1 1
6
dt 6
dt
t 1
t 1
3
2
1
t
t
2
6 t t 1 dt 6
dt 6 t 6 ln t 1 C
t 1
3 2
2t 3 3t 2 6t 6 ln t 1 C 2 x 33 x 66 x 6 ln 6 x 1 C.
56.
2°. Інтегрування диференціальних біномівОзн. Вираз виду
x a bx
m
n p
m, n, p Q, a, b R
називається диференціальним біномом.
Теорема 1. (теорема Чебишева). Інтеграл від
диференціального бінома виражається через інтеграл від
раціональної функції відносно нової змінної, якщо
p Z
m 1
Z
n
m 1
p Z
n
s НСK(m, n )
s LСM( m, n )
x ts
r знаменник дробу p
a bx n t r
r знаменник дробу p
ax n b t r
57.
3°. Інтеграли видуR sin x, cos x dx
раціоналізуються підстановкою
x
t tg
2
x
2 tg
2 2t
sin x
2
1
t
2 x
1 tg
2
x
1 tg
2
1
t
2
cos x
2
1
t
2 x
1 tg
2
2
x
x 2 arctg t
dx
2
dt
2
1 t
R sin x, cos x dx R (t )dt
1
58.
б)R sin x cos xdx
R cos x sin xdx
в)
R tg x dx
г)
R sin x, cos x dx
a)
sin x t
cos x t
tg x t
R sin x, cos x R sin x, cos x
sin x t
R sin x, cos x R sin x, cos x
cos x t
R sin x, cos x R sin x, cos x
tg x t
59.
д)m
n
sin
x
cos
xdx
n Z ; n 0; n непарне
m Z ; m 0; m непарне
n, m Z; n 0, m 0; n, m непарнi
m max( m, n)
n max( m, n)
n, m Z; n 0, m 0; n, m непарнi
n, m Z; n 0, m 0; n, m непарнi
sin x t
cos x t
sin x t
cos x t
sin x t
cos x t
60.
д)m
n
sin
x
cos
xdx
1 cos 2 x
cos x
2
1 cos 2 x
2
sin x
2
2
n, m Z ; n 0, m 0; n, m парнi
n, m Z ; n m 0; n, m парнi
n, m Z ; n 0, m 0; n, m непарнi
tg x t
61.
е)sin ax cos bxdx, sin ax sin bxdx, cos ax cos bxdx
1
sin cos sin( ) sin( )
2
1
sin sin cos( ) cos( )
2
1
cos cos cos( ) cos( )
2
62.
63.
1°. Виділення повного квадрата.dx
ax 2 bx c
x
dx
x 2x 5
2
ax 2 bx c
x 2 x 1 1 1 5
2
2 x 1 1 1 5
2
dx
dx
2
dx
du
u2 A
2
dx
x 1
2
4
ln u u 2 A C
d x 1
x 1
2
4
64.
1°. Виділення повного квадрата.dx
ax 2 bx c
x
dx
x 2x 5
2
dx
2
ln x 1
ax 2 bx c
dx
x 2 x 1 1 1 5
2
2 x 1 1 1 5
2
dx
2
x 1 2 4 C
dx
x 1
2
4
d x 1
x 1
2
ln x 1 x 2 2 x 5 C
4
65.
2°. Утворення в чисельнику диференціала знаменника.Ax B
ax 2 bx c dx
Ax B
ax bx c
2
dx
1
x
3x 1
t x2 4 x 5
3 dx
dx
3 2
2
x 4x 5
x 4x 5
dt (2 x 4)dx
2
2
2 x 4 4
2x
3
3
3 dx
3
2
dx
2
2 x 4x 5
2
x 4x 5
2
4
3 2 x 4
3
2
dx 2 3
dx
2 x 4x 5
2 x 4x 5
3
3 10
1
2
ln x 4 x 5 2
dx
2
2 3 x 4x 5
66.
31
2
ln x 4 x 5 5 2
dx
x 4 x 4 4 5
2
3
1
2
ln x 4 x 5 5
dx
2
2
x 2 9
3
d x 2
2
ln x 4 x 5 5
2
2
2
x 2 3
3
1
x 2 3
2
ln x 4 x 5 5
ln
C
2
2 3 x 2 3
3
5 x 5
2
ln x 4 x 5 ln
C
2
6 x 1
67.
1.8. Інтеграли, що «не беруться»e
x2
2
cos
x
dx,
dx
2
sin
x
dx
dx
ln x
— інтеграл Пуассона
— інтеграли Френеля
— інтегральний логарифм
sin x
x dx
— інтегральний синус
cos x
x dx
— інтегральний косинус

















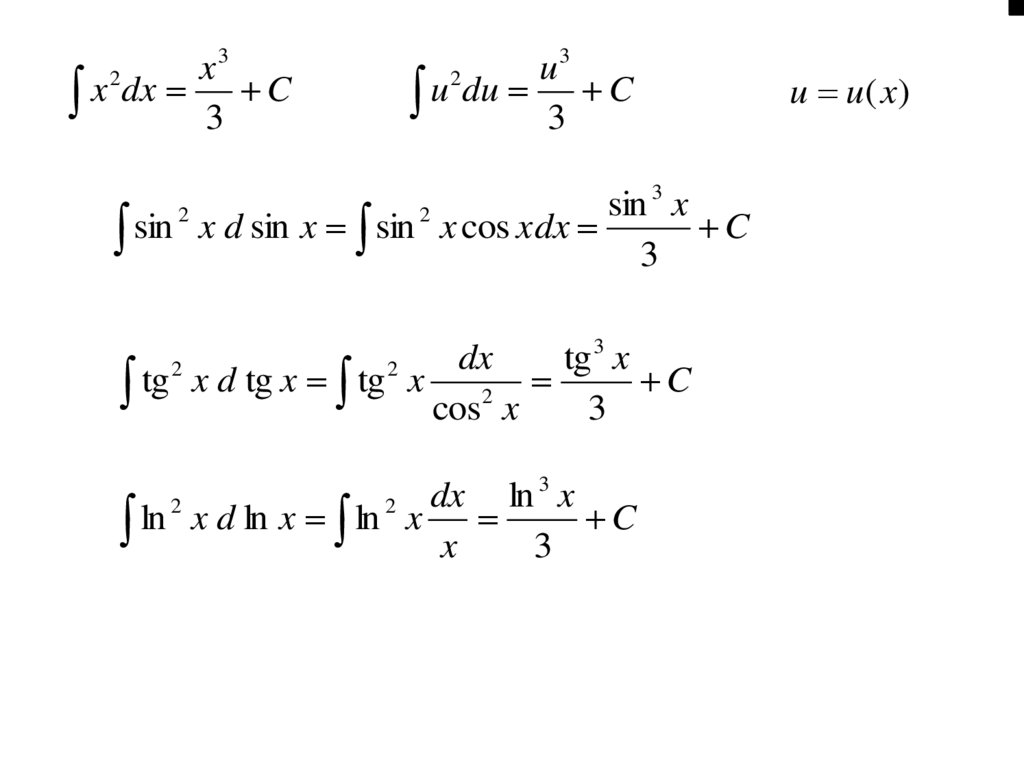




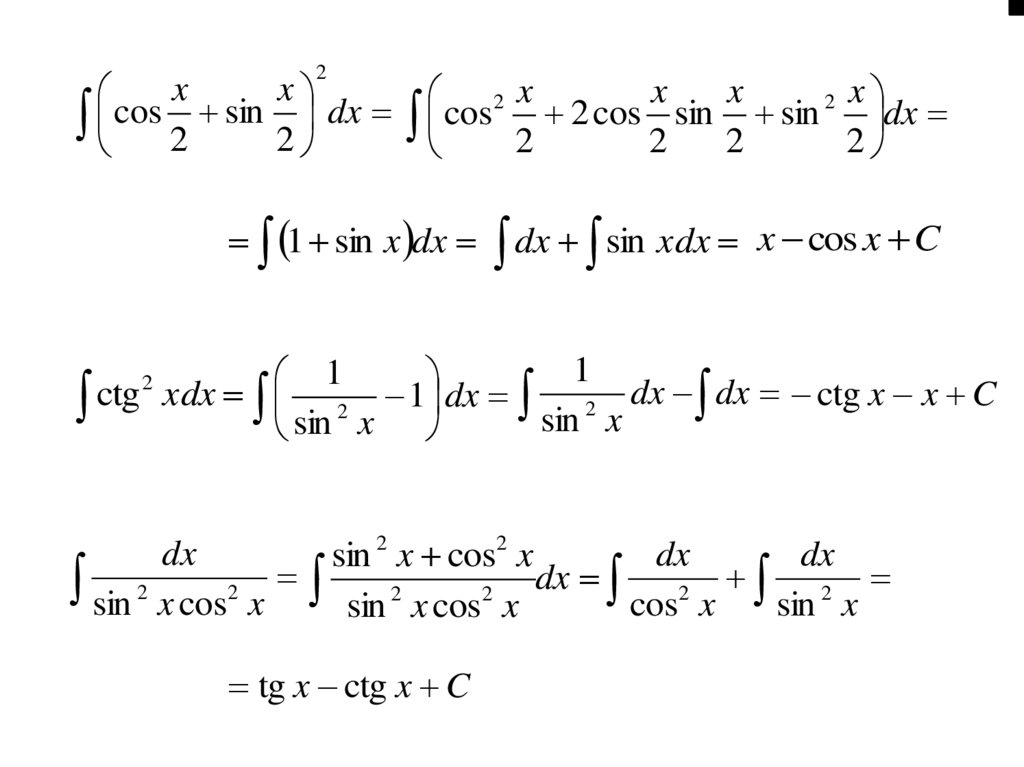

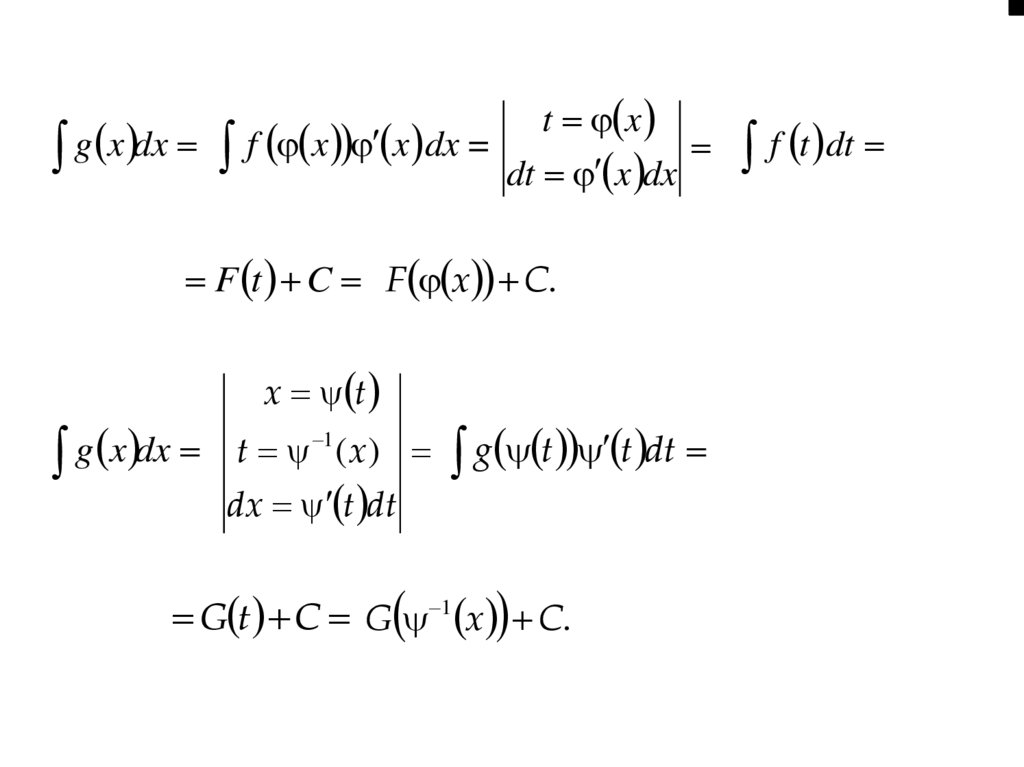
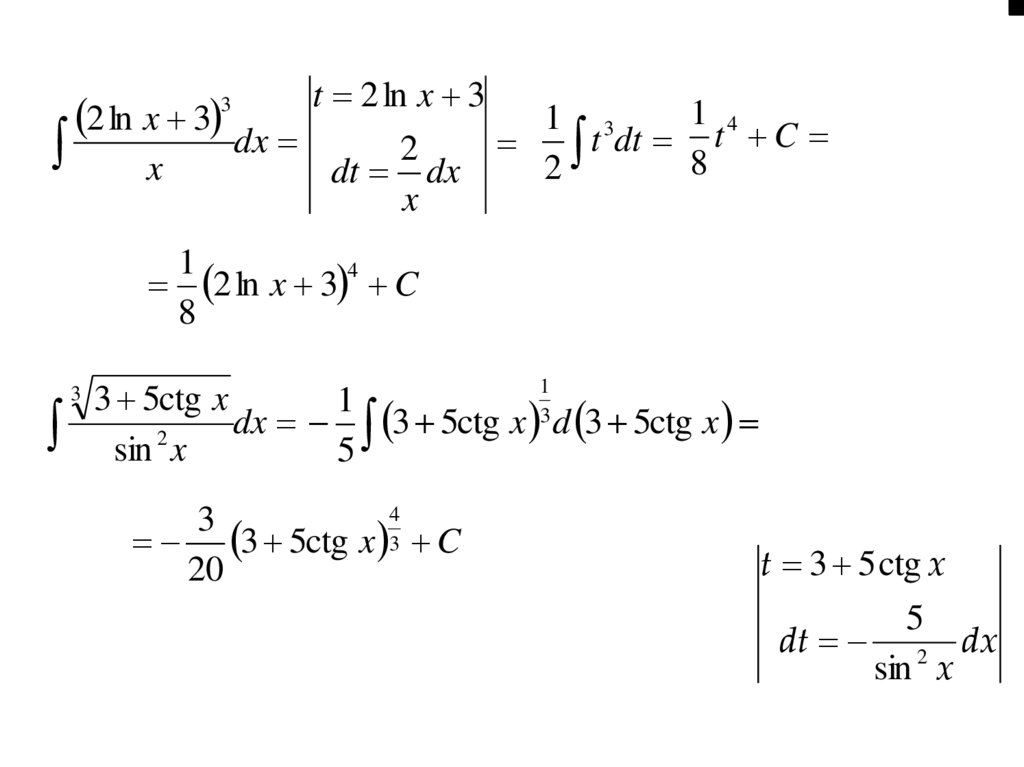

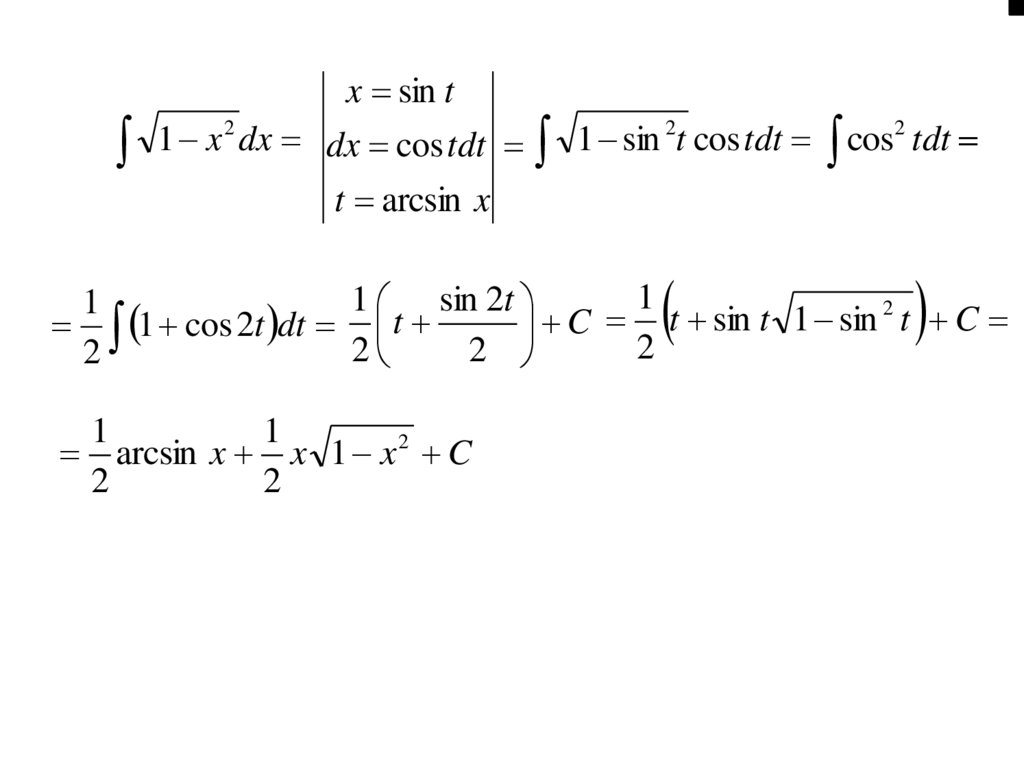
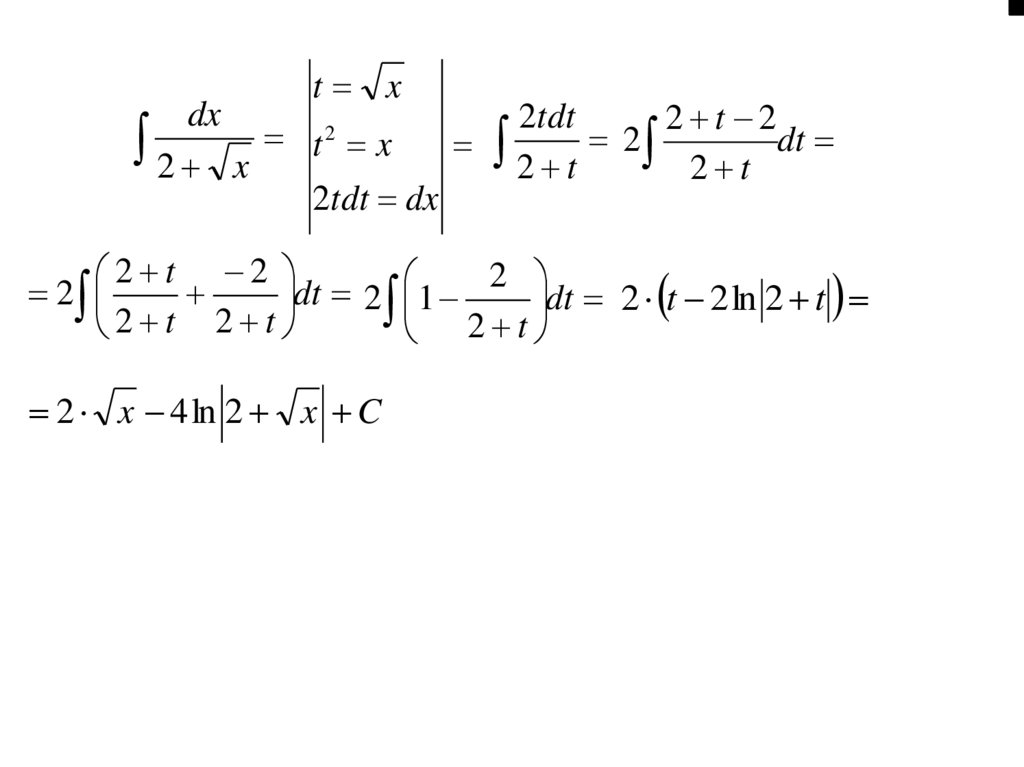








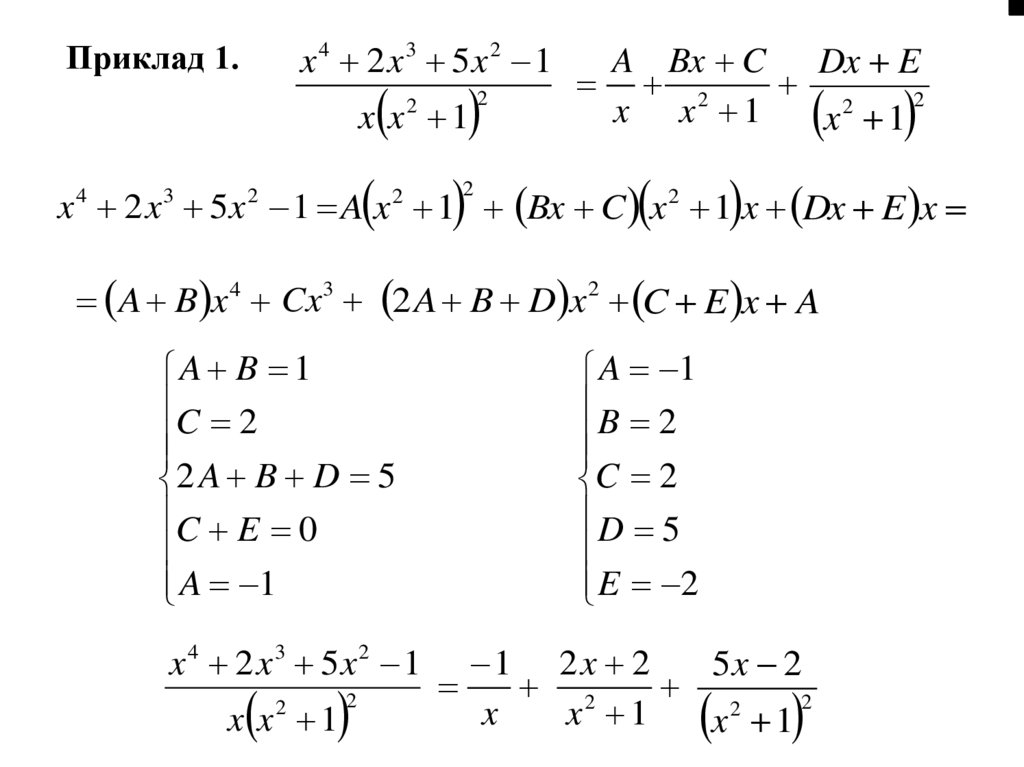
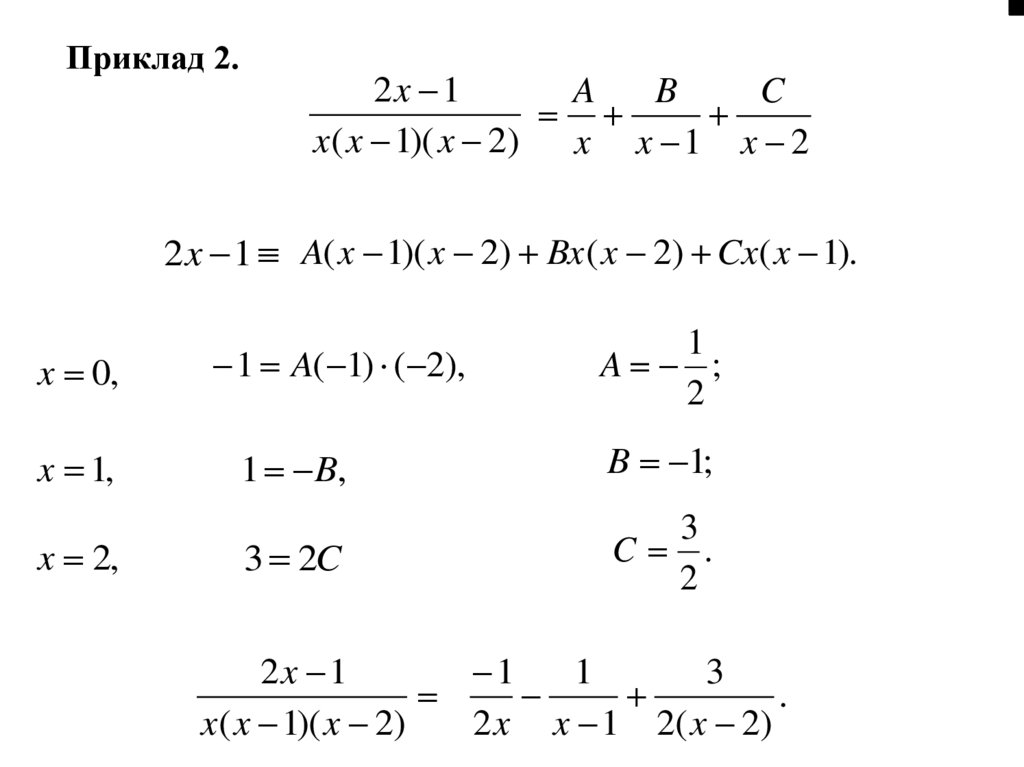

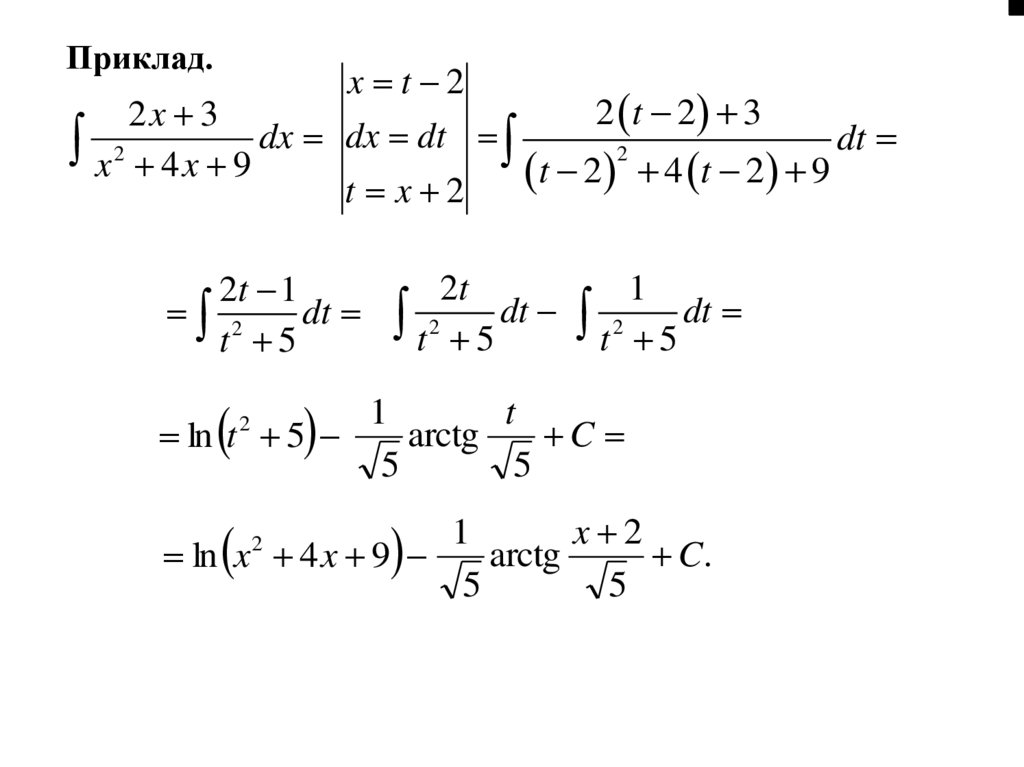



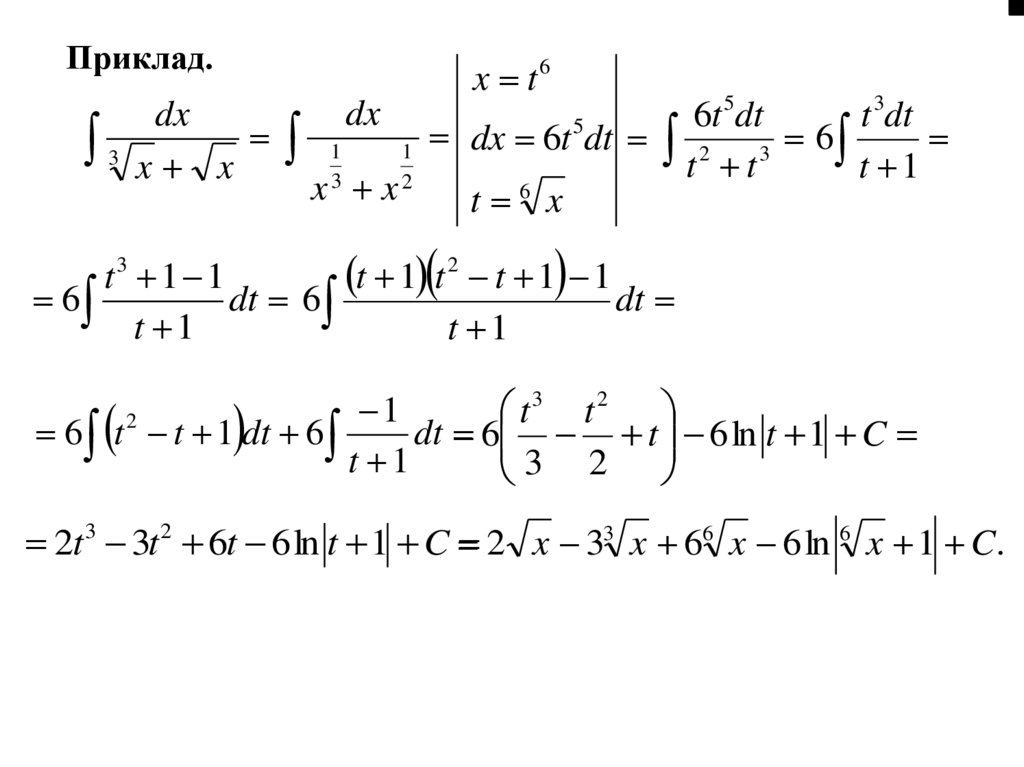



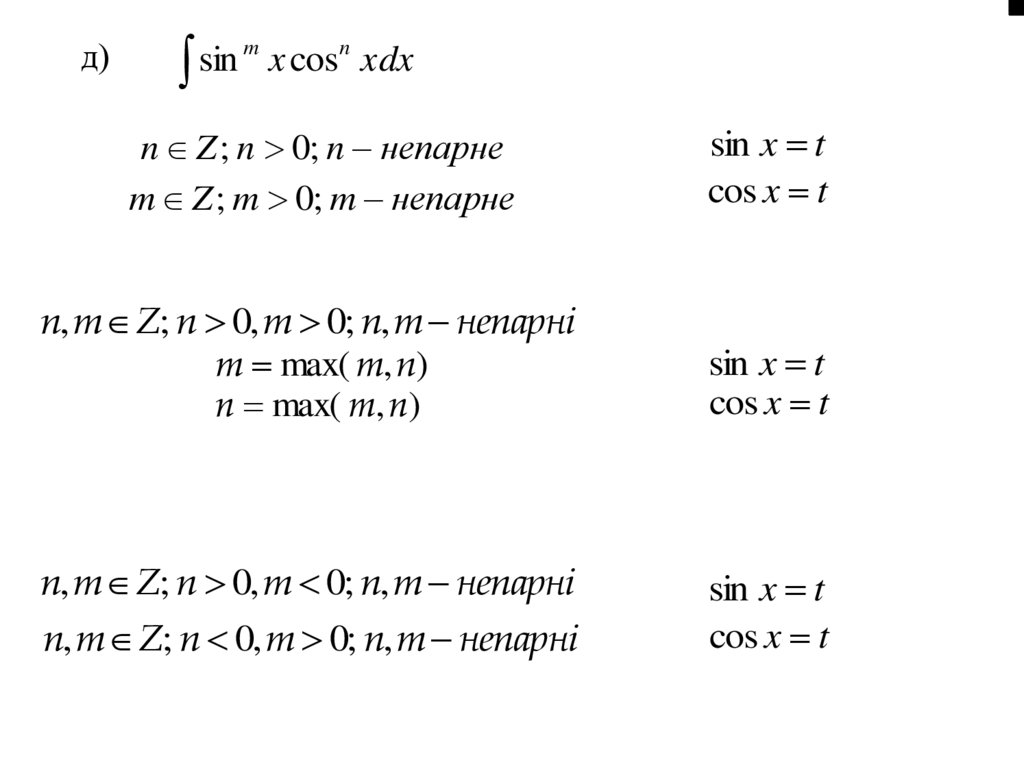

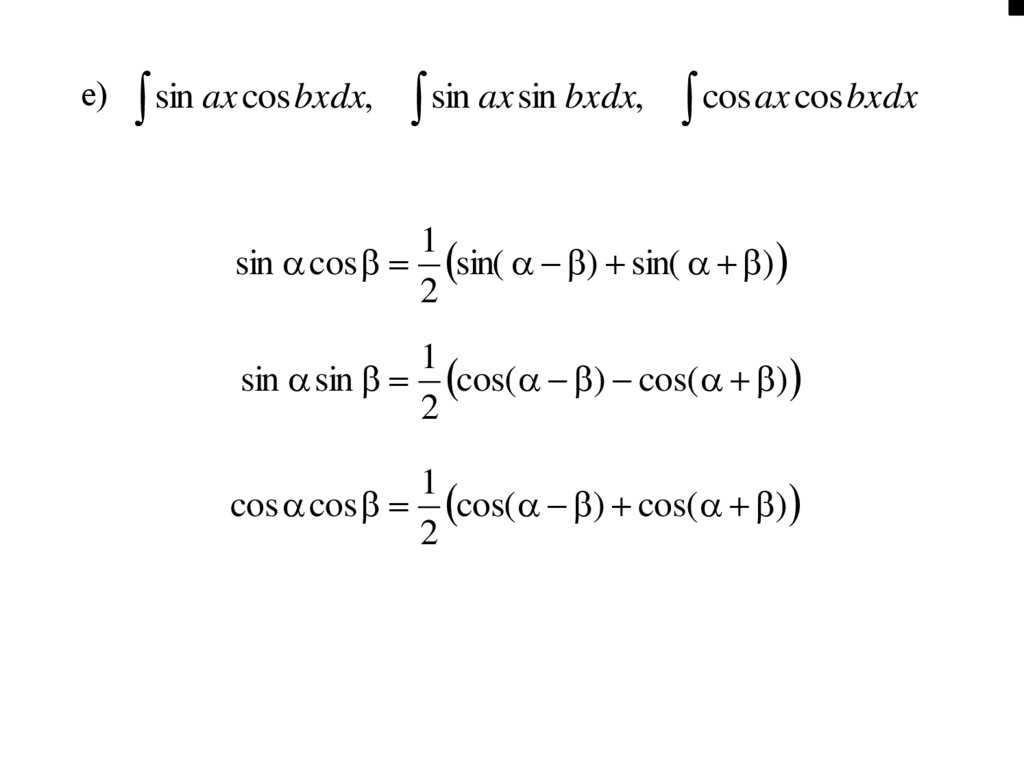




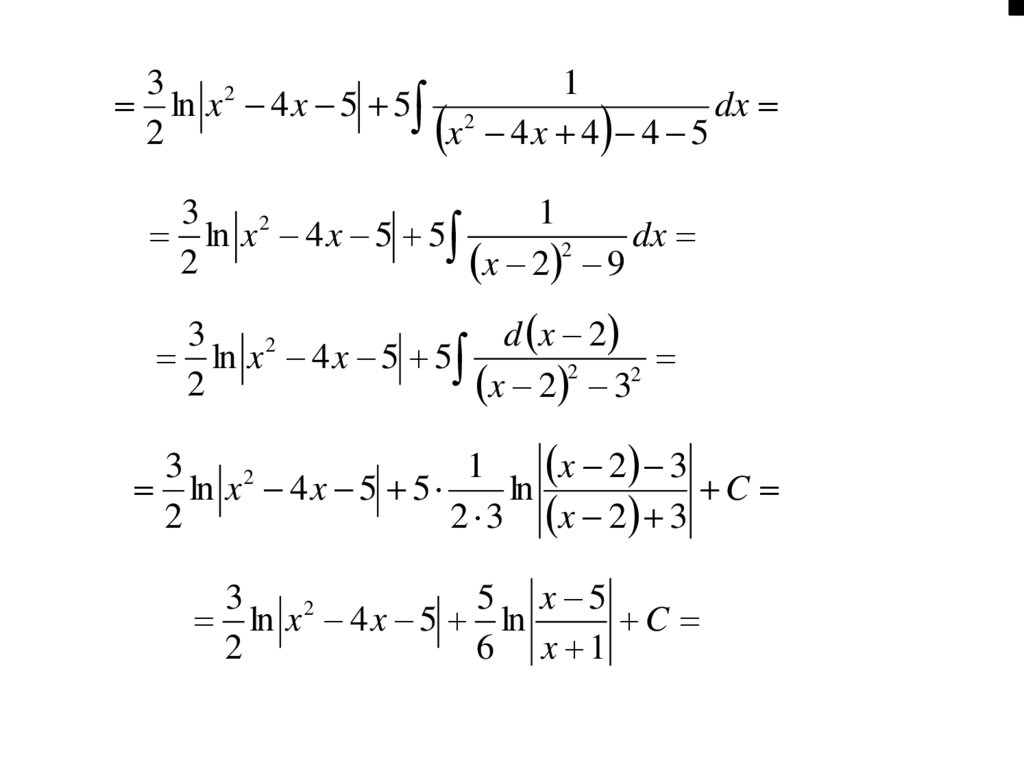


 Математика
Математика








