ეკონომიკისა და ბიზნესის სტატისტიკა. ცენტრალური ტენდენციის მახასიათებლები. თემა 2

1.

ეკონომიკისა და ბიზნესის
სტატისტიკა
თემა 2
ცენტრალური ტენდენციის
მახასიათებლები

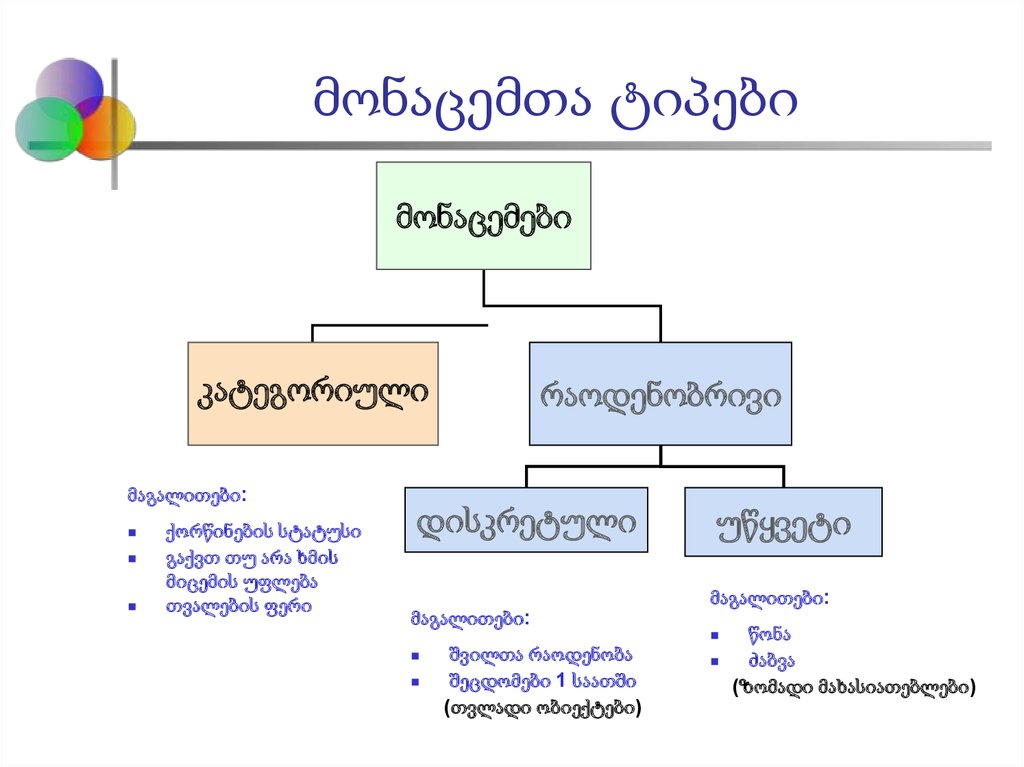
2. მონაცემთა ტიპები

მონაცემები
კატეგორიული
მაგალითები:
ქორწინების სტატუსი
გაქვთ თუ არა ხმის
მიცემის უფლება
თვალების ფერი
რაოდენობრივი
დისკრეტული
უწყვეტი
მაგალითები:
მაგალითები:
შვილთა რაოდენობა
შეცდომები 1 საათში
(თვლადი ობიექტები)
წონა
ძაბვა
(ზომადი მახასიათებლები)

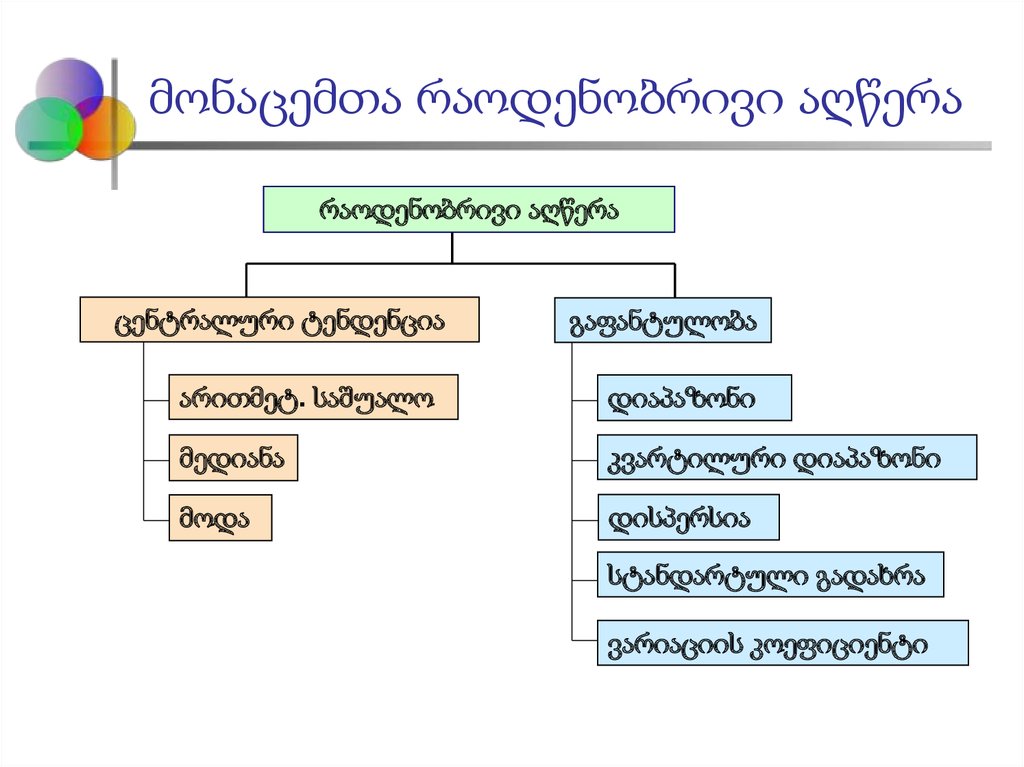
3. მონაცემთა რაოდენობრივი აღწერა

რაოდენობრივი აღწერა
ცენტრალური ტენდენცია
გაფანტულობა
არითმეტ. საშუალო
დიაპაზონი
მედიანა
კვარტილური დიაპაზონი
მოდა
დისპერსია
სტანდარტული გადახრა
ვარიაციის კოეფიციენტი

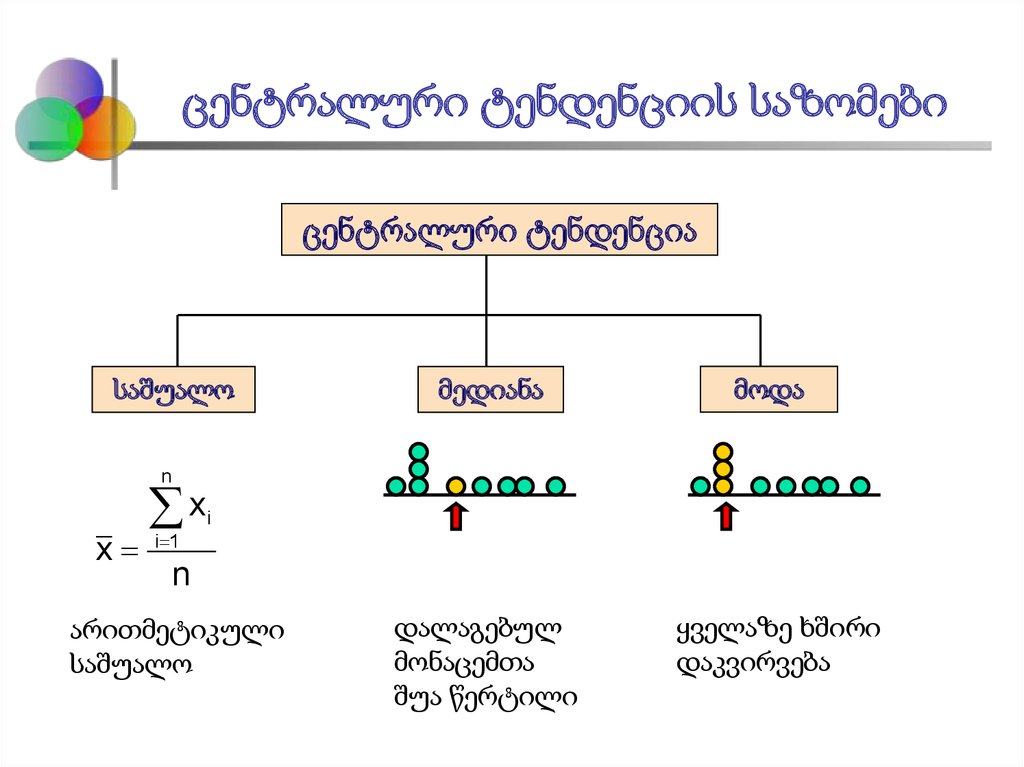
4. ცენტრალური ტენდენციის საზომები

ცენტრალური ტენდენცია
საშუალო
მედიანა
მოდა
n
x
x
i 1
i
n
არითმეტიკული
საშუალო
დალაგებულ
მონაცემთა
შუა წერტილი
ყველაზე ხშირი
დაკვირვება

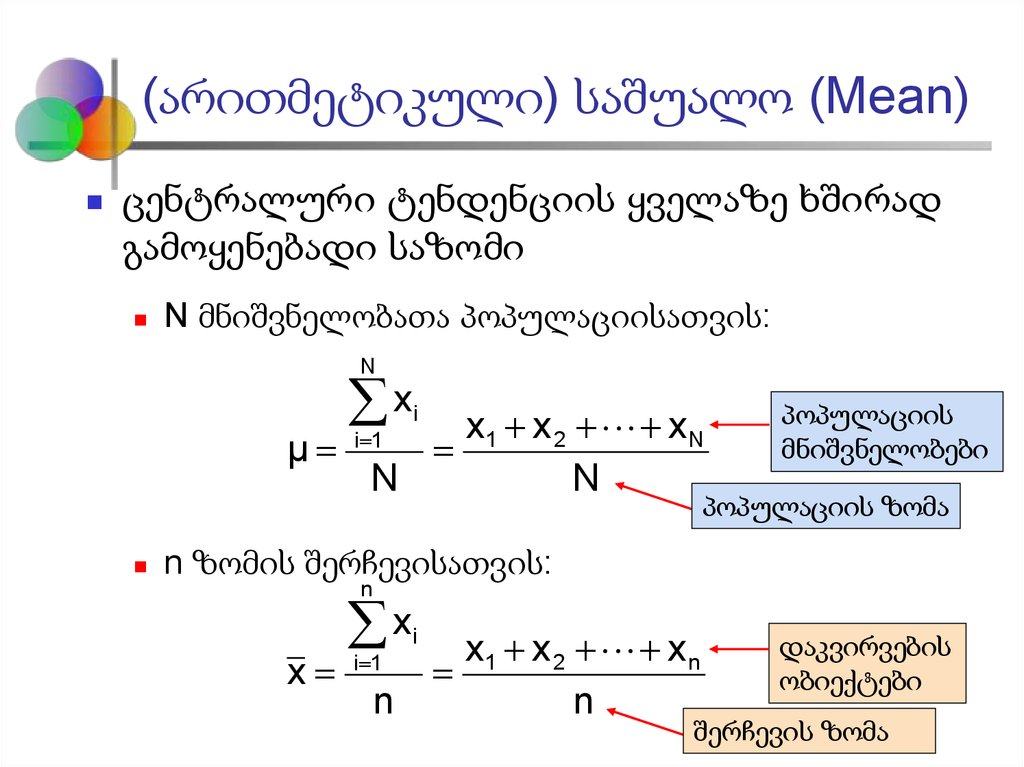
5. (არითმეტიკული) საშუალო (Mean)

ცენტრალური ტენდენციის ყველაზე ხშირად
გამოყენებადი საზომი
N მნიშვნელობათა პოპულაციისათვის:
N
x
x1 x 2 x N
i 1
μ
N
N
i
პოპულაციის
მნიშვნელობები
პოპულაციის ზომა
n ზომის შერჩევისათვის:
n
x
x
i 1
n
i
x1 x 2 x n
n
დაკვირვების
ობიექტები
შერჩევის ზომა

6. არითმეტიკული საშუალო

(გაგრძ.)
საშუალო = მნიშვნელობათა ჯამი გაყოფილი
მნიშნელობათა რაოდენობაზე
იცვლება ექსტრემალური (ამოვარდნილი)
მნიშვნელობების (outliers) გამო
0 1 2 3 4 5 6 7 8 9 10
საშუალო= 3
1 2 3 4 5 15
3
5
5
0 1 2 3 4 5 6 7 8 9 10
საშუალო = 4
1 2 3 4 10 20
4
5
5

7. მედიანა

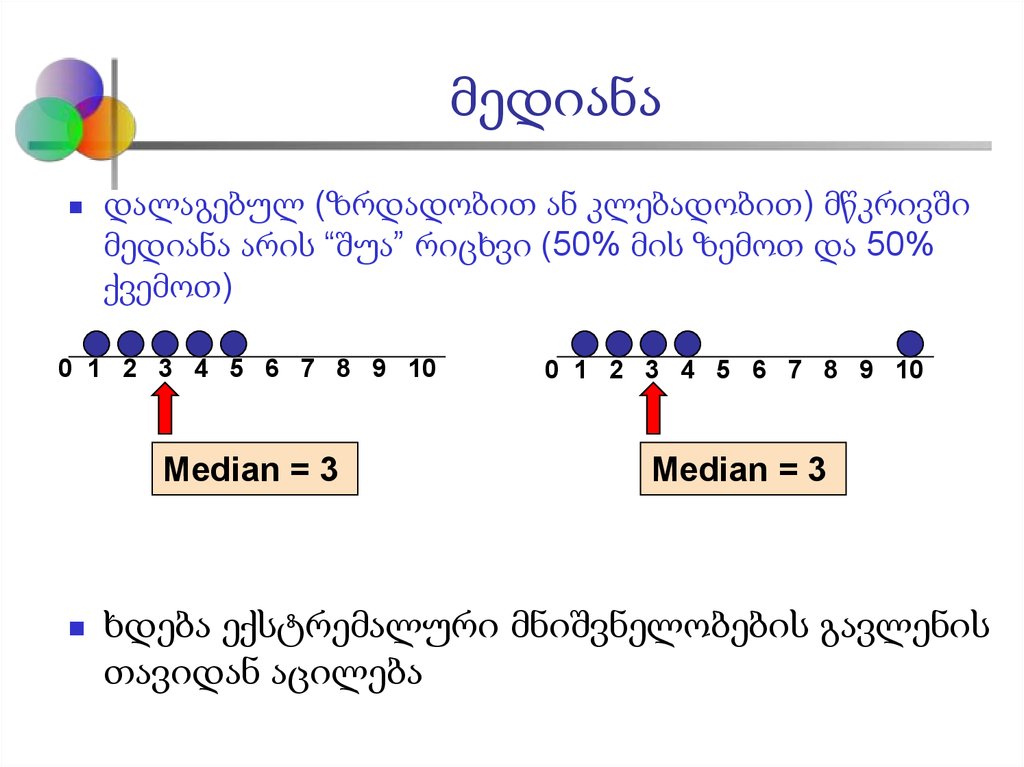
დალაგებულ (ზრდადობით ან კლებადობით) მწკრივში
მედიანა არის “შუა” რიცხვი (50% მის ზემოთ და 50%
ქვემოთ)
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
Median = 3
Median = 3
ხდება ექსტრემალური მნიშვნელობების გავლენის
თავიდან აცილება

8. მედიანის პოვნა

მედიანის მდებარეობა = დალაგებული მონაცემების
n 1 -ე წევრი
2
თუ რიცხვთა ოდენობა კენტია, მედიანა შუა
წერტილია
თუ რიცხვთა ოდენობა ლუწია, მედიანა არის ორი
შუა წერტილის საშუალო

9. მოდა

ცენტრალური ტენდენციის საზომი
ყველაზე ხშირი მოვლენა
ექსტრემალური მნიშვნელობების გავლენას ადგილი
არ აქვს
გამოიყენება რაოდენობრივი და კატეგორიული
მონაცემებისათვის
შესაძლებელია გვქონდეს რამდენიმე ან არც ერთი
მოდა
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
მოდა = 9
0 1 2 3 4 5 6
არც ერთი
მოდა

10. მაგალითი: გამეორება

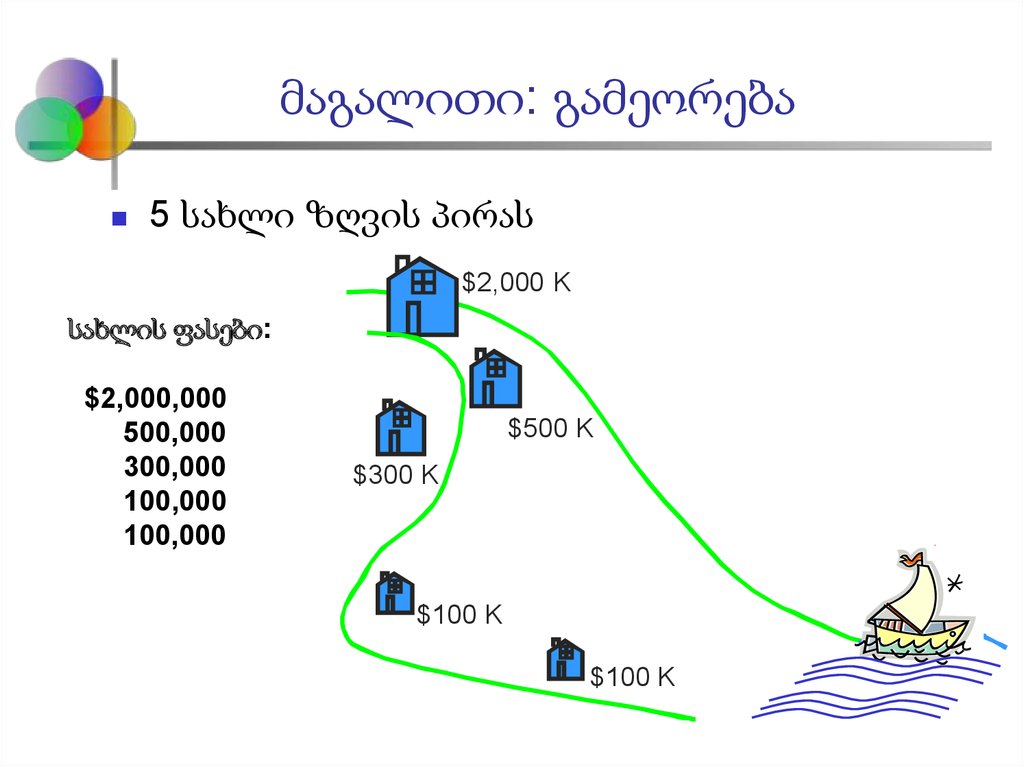
5 სახლი ზღვის პირას
$2,000 K
სახლის ფასები:
$2,000,000
500,000
300,000
100,000
100,000
$500 K
$300 K
$100 K
$100 K

11. შემაჯამებელი სტატისტიკები

სახლის ფასები:
$2,000,000
500,000
300,000
100,000
100,000
საშუალო:
მედიანა: დალაგებულ მონაცემთა შუა
წერტილი
ჯამი 3,000,000
($3,000,000/5)
= $600,000
= $300,000
მოდა: ყველაზე ხშირი მნიშვნელობა
= $100,000

12. მდებარეობის რომელი საზომია “საუკეთესო”?

ძირითადად გამოიყენება საშუალო, თუ
არ არის ამოვარდნილი მნიშვნელობები
ასეთ შემთხვევაში გამოიყენება მედიანა,
რადგან ის არ არის მგრძნობიარე
ამოვარდნილი მნიშვნელობების მიმართ.
მაგალითი: სახლის მედიანური ფასების
გამოყენება რეგიონისთვის – ნაკლებად
მგრძნობიარე ამოვარდნილი
მნიშვნელობების მიმართ

13. კვარტილები

კვარტილები ყოფენ ზრდადობით (კლებადობით)
დალაგებულ მონაცემებს 4 სეგმენტად, რომლებიც
შეიცავს მნიშნელობათა თანაბარ რაოდენობებს.
25%
Q1
25%
25%
Q2
25%
Q3
პირველი კვარტილი, Q1, არის მნიშვნელობა, რომელზეც
დაკვირვებათა 25% უფრო ნაკლებია და 75% – უფრო
მეტი.
Q2 არის იგივე რაც მედიანა (50% უფრო ნაკლები, 50%
უფრო მეტი)
მესამე კვარტილისთვის (Q3) მხოლოდ დაკვირვებათა
25% არის უფრო მეტი

14. შეწონილი საშუალო

მონაცემთა სიმრავლის შეწონილი საშუალო
არის
n
w x
x
w
i 1
i
i
w1x1 w 2 x 2 w n x n
wi
სადაც wi არის i–ური დაკვირვების წონა
გამოიყენება, როდესაც მონაცემები უკვე
დაჯგუფებულია n კლასად, სადაც i–ურ კლასში
მოქცეულია wi ოდენობის მნიშვნელობები