Лекция_9_Одномерная_оптимизация_1

1. Одномерная оптимизация

Численные методы поиска экстремумов функции одной
переменной

2. Постановка задачи

Задачей одномерной оптимизации является нахождение точек локального
минимума и соответствующих им значений функции, а в некоторых случаях
требуется вычислить глобальный минимум. Однако, во всех случаях эта задача
сводится к задаче нахождения локального минимума.
Интервал, на котором локализован единственный минимум, называется
отрезком
неопределенности,
а
(одноэкстремальной) на этом отрезке.
функцию
называют
унимодальной

3. Постановка задачи

Суть методов одномерного поиска заключается в том, что на каждой
итерации интервал неопределенности уменьшается и стягивается к точке
минимума. Уменьшение отрезка происходит до тех пор, пока на некоторой
n-й итерации отрезок неопределенности bn;an не станет соизмеримым с
заданной погрешностью , то есть будет выполняться условие |bn-an| < .
Тогда за точку минимума можно принять любую точку, принадлежащую
этому отрезку, в частности, его середину.

4. Метод сканирования с постоянным шагом

Разделим интервал неопределенности на некоторое число равных частей
и вычислим значение целевой функции в точках разбиения. Очевидно, что за
минимум принимают наименьшее из этих значений – это так называемый
метод сканирования.
Каким должен быть шаг, чтобы требуемая точность Ех была достигнута?

5. Метод сканирования с переменным шагом

От начальной точки интервала неопределенности [a,b] двигаются с
начальным шагом (h) до тех пор, пока функция в точках разбиения
уменьшается (т.е. функция убывает). Если функция в очередной точке стала
возрастать, то происходит сужение интервала неопределенности путем
возврата от рассматриваемой (которая станет правой границей нового
интервала) точки x на два шага назад. При этом левой границей нового
отрезка неопределенности станет точка a=x-2h, а правой b=x. Новый отрезок
вновь исследуют таким же образом, но уже с уменьшенным в два раза
шагом: h=h/2. Процесс повторяется до момента достижения заданной
точности минимума |bn-an| < .

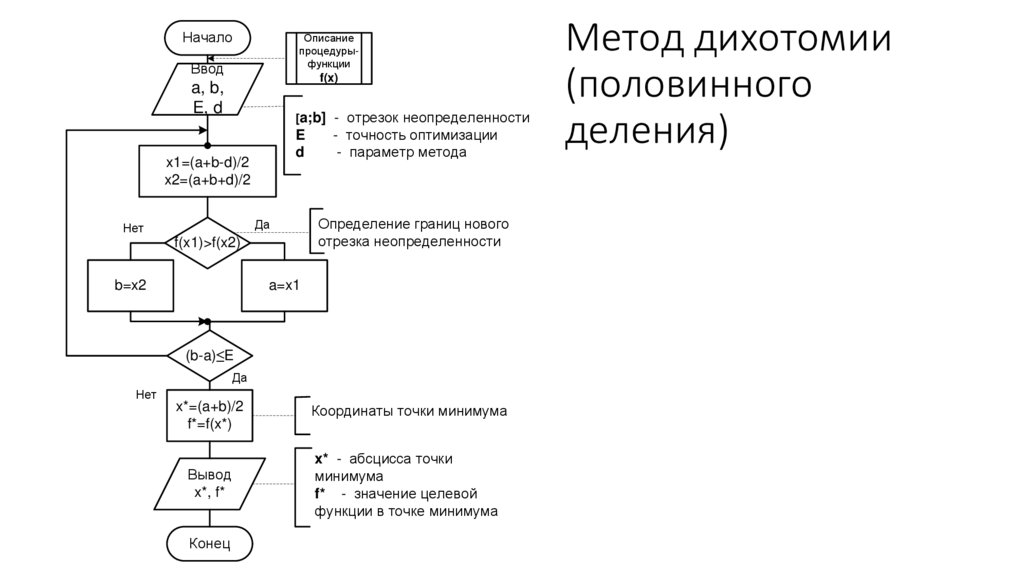
6. Метод дихотомии (половинного деления)

Начало
Описание
процедурыфункции
Ввод
f(x)
a, b,
E, d
[a;b] - отрезок неопределенности
E
d
x1=(a+b-d)/2
x2=(a+b+d)/2
Да
Нет
f(x1)>f(x2)
b=x2
- точность оптимизации
- параметр метода
Определение границ нового
отрезка неопределенности
a=x1
(b-a)≤E
Да
Нет
x*=(a+b)/2
f*=f(x*)
Координаты точки минимума
Вывод
x*, f*
x* - абсцисса точки
минимума
f* - значение целевой
функции в точке минимума
Конец
Метод дихотомии
(половинного
деления)

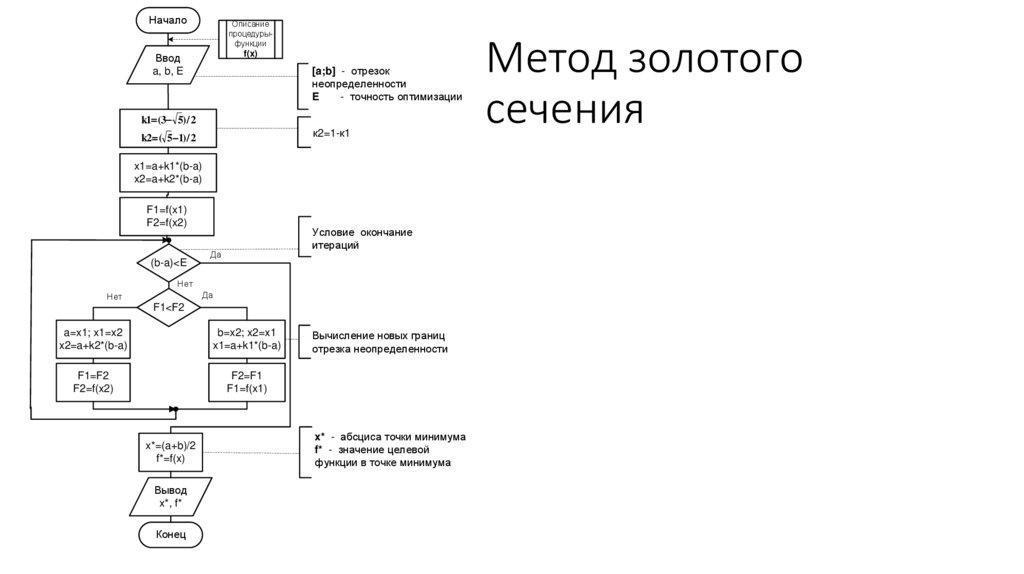
7. Метод золотого сечения

Начало
Описание
процедурыфункции
f(x)
Ввод
a, b, E
[a;b] - отрезок
неопределенности
E
- точность оптимизации
k1 (3 5) / 2
к2=1-к1
k2 ( 5 1) / 2
x1=a+k1*(b-a)
x2=a+k2*(b-a)
F1=f(x1)
F2=f(x2)
(b-a)<E
Условие окончание
итераций
Да
Нет
Да
Нет
F1<F2
a=x1; x1=x2
x2=a+k2*(b-a)
b=x2; x2=x1
x1=a+k1*(b-a)
F1=F2
F2=f(x2)
F2=F1
F1=f(x1)
x*=(a+b)/2
f*=f(x)
Вывод
x*, f*
Конец
Вычисление новых границ
отрезка неопределенности
x* - абсциса точки минимума
f* - значение целевой
функции в точке минимума
Метод золотого
сечения