Похожие презентации:
Л_1_3_1_Механическая_работа_и_энергия_н
1. Механическая работа и энергия
Сегодня воскресенье, 7 декабря 2025 г.Механическая работа
и энергия
2.
Механическая работа и энергия1. Механическая работа,
мощность, энергия.
2. Кинетическая энергия.
3. Потенциальная энергия.
4. Закон сохранения энергии.
Закон сохранения импульса.
3.
ЛитератураТрофимова Т.И. Физика.- М.: Академия, 2013 г.
§ 5-8, § 23, – 352 с.
Трофимова Т.И. Курс физики _ М.: Академия,
2014 г. § 7-13. -560 с.
БЭУ Физика (электронный учебник) –СанктПетербург, 2017.
Дополнительная
Физические основы механики. Практикум. –
Севастополь: ЧВВМУ им. П.С. Нахимова, 2021,
гл.3, с. 76-84.
Конспект лекций.
4. 1. Механическая работа, мощность, энергия
Изменение механического движения телавызывается силами, действующими на него
со стороны других тел. Чтобы количественно
характеризовать процесс обмена энергией
между взаимодействующими телами, в
механике вводится понятие работы силы.
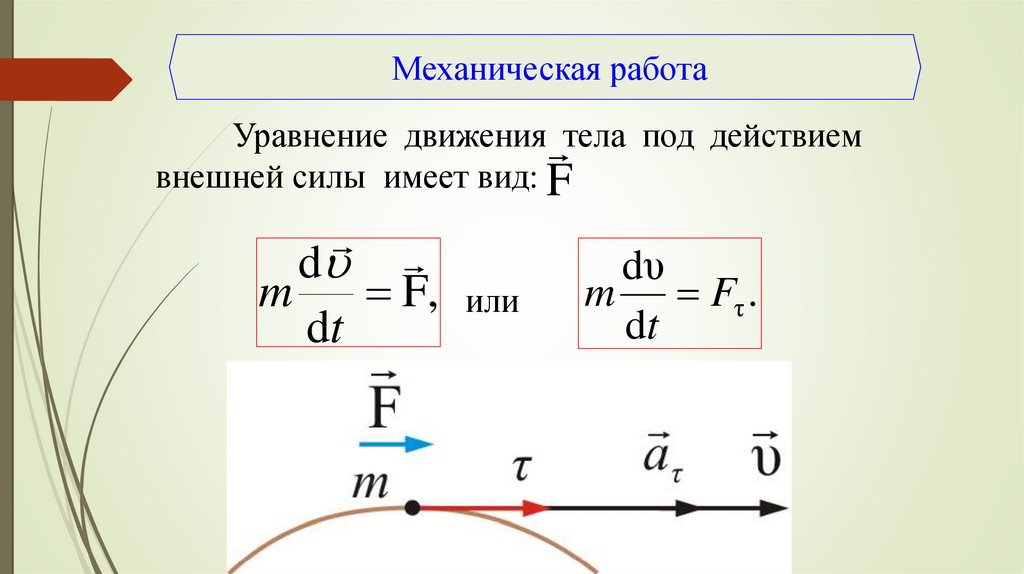
5. Механическая работа
Уравнение движения тела под действиемвнешней силы имеет вид: F
d
m
F, или
dt
dυ
m Fτ .
dt
6.
dυm Fτ .
dt
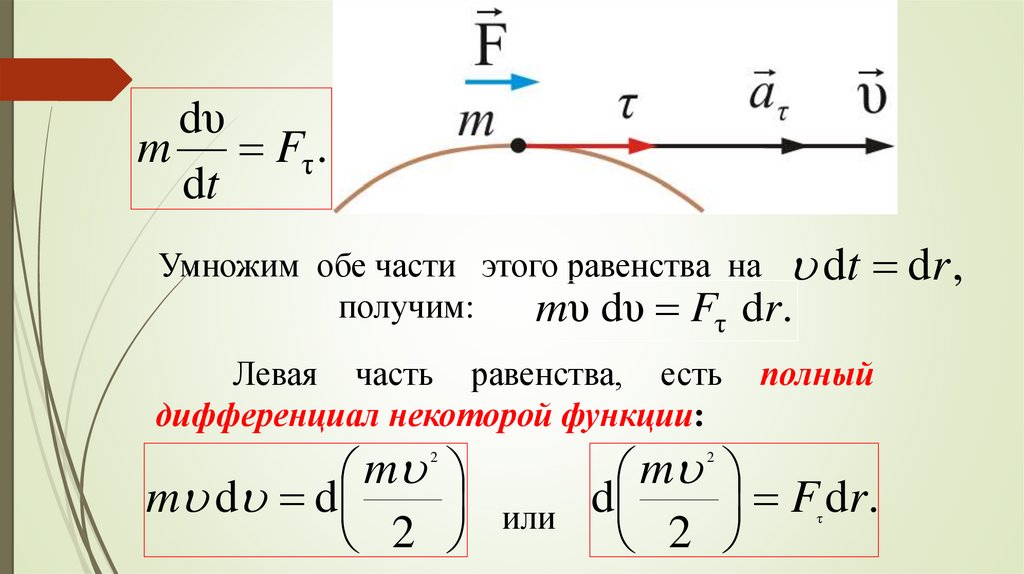
Умножим обе части этого равенства на dt dr ,
получим:
mυ dυ Fτ dr.
Левая часть равенства, есть
дифференциал некоторой функции:
m
m d d
2
2
полный
m
d
F dr.
2
2
или
τ
7.
Т.о.m
d
F dr.
2
2
τ
Если система замкнута, то
F
внеш.
m
d
0.
2
0 и
2
F 0, тогда и
Если полный дифференциал некоторой
функции, описывающей поведение системы
равен нулю, то эта функция может служить
характеристикой
состояния
данной
системы.
8.
2. Кинетическая энергияФункция
состояния
системы,
определяемая только скоростью ее движения,
называется кинетической энергией.
m
Wk
.
2
2
Кинетическая энергия системы есть функция
состояния движения этой системы.
Wk – аддитивная величина:
2
n
mi i
Wk
,
2
i 1
9.
Связь кинетической энергии с работой.Если постоянная сила действует на тело, то оно
будет двигаться в направлении силы. Тогда,
элементарная работа по перемещению тела из т. 1 в т. 2,
будет равна произведению силы F на перемещение dr :
dA Fdr
10.
dA Fdr , отсюда A Fdr.d
F ma m ,
Т.к. нам известно, что
dt
а dr dt ,
тогда после замены получим
2
1
выражение для работы:
m m
A Fdr m d
.
2
2
2
2
1
2
2
2
1
1
Окончательно получаем:
2
A Fdr Wk 2 Wk1.
1
11.
Следовательно, работа силы приложеннойк телу на пути r численно равна изменению
кинетической энергии этого тела:
A Wk.
Или изменение кинетической энергии
dWk равно работе внешних сил:
dWk dA.
Работа, так же как и кинетическая энергия,
измеряется в джоулях.
12.
Скорость совершения работы (передачиэнергии) называется мощность.
Мощность есть работа, совершаемая в
единицу времени.
Мгновенная
или
мощность
dr
N F F .
dt
Средняя мощность
dA
N
dt
A
N .
t
Измеряется мощность в ваттах. 1 Вт = 1 Дж/с.
13. Консервативные силы и системы
Кромеконтактных
взаимодействий,
наблюдаются взаимодействия между телами,
удаленными друг от друга. Подобное
взаимодействие осуществляется посредством
физических полей (особая форма материи).
Каждое тело создает вокруг себя поле,
которое проявляет себя именно воздействием
на другие тела.
14.
Силы, работа которых не зависит отпути, по которому двигалось тело, а зависит
от начального и конечного положения тела
называются консервативными.
Обозначим A – работа консервативных
сил, по перемещению тела из т. 1 в т. 2
Рисунок 1
15.
A1a 2 A1b 2 A1l 2 A12 .Изменение направления движения на
противоположное – вызывает изменение знака
работы консервативных сил. Отсюда следует,
что работа консервативных сил вдоль
замкнутой кривой равна нулю:
Fdr A A A A 0
12
21
12
12
S
Интеграл по замкнутому контуру S,
– называется циркуляцией вектора F
Fdr
S
16.
Если циркуляция какого-либо векторасилы равна нулю, то эта сила консервативна.
Консервативные силы: сила тяжести,
электростатические силы, силы центрального
стационарного поля.
Неконсервативные силы: силы трения,
силы вихревого электрического поля.
Консервативная
система
–
такая,
внутренние
силы
которой
только
консервативные, внешние – консервативны и
стационарны.
Пример
консервативных
сил
–
гравитационные силы (рисунок 2).
17.
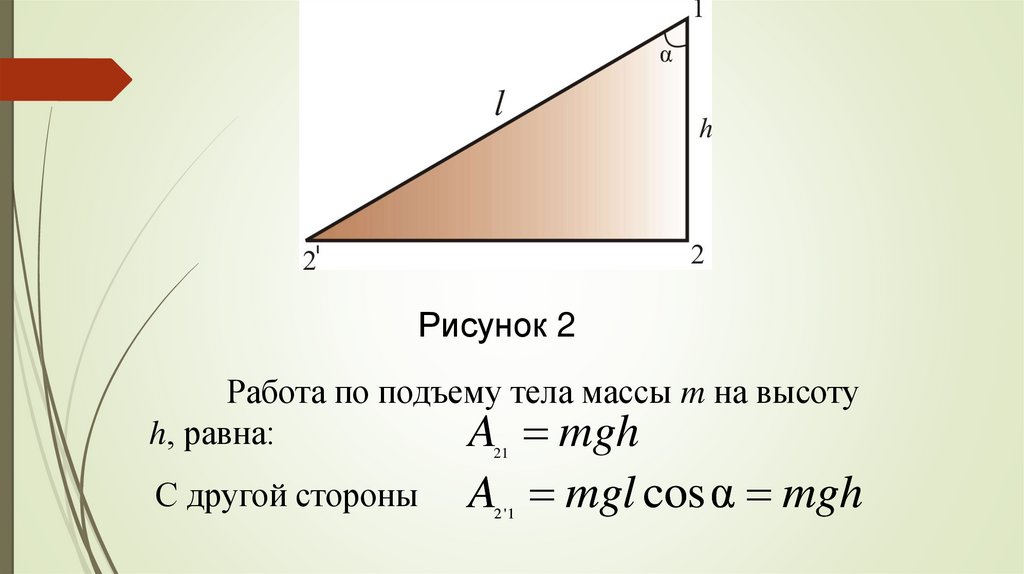
Рисунок 2Работа по подъему тела массы m на высоту
h, равна:
A21 mgh
С другой стороны
A mgl cos α mgh
2 '1
18.
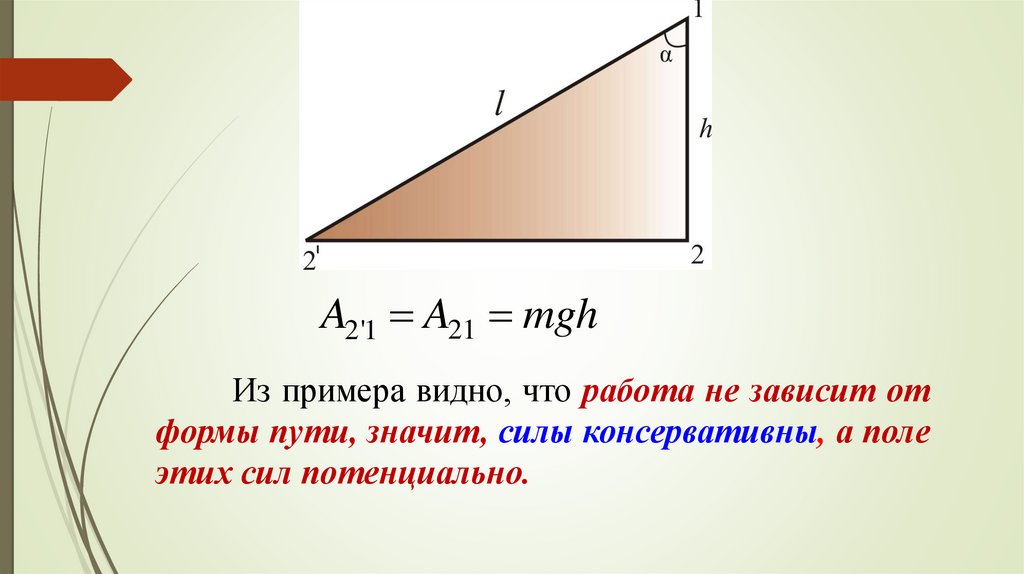
A2'1 A21 mghИз примера видно, что работа не зависит от
формы пути, значит, силы консервативны, а поле
этих сил потенциально.
19.
3. Потенциальная энергия.Если на систему материальных тел действуют
консервативные силы, то можно ввести понятие
потенциальной энергии.
Работа, совершаемая консервативными силами при
изменении конфигурации системы, то есть при
изменении положения тел относительно системы
отсчета, не зависит от того, как было осуществлено это
изменение. Работа определяется только начальной и
конечной конфигурациями системы:
20.
A12 Wp1 Wp 2 ,здесь потенциальная энергия Wp(х, у, z) – функция
состояния системы, зависящая только от
координат всех тел системы в поле консервативных
сил.
Итак, Wk – определяется скоростью движения
тел системы, а Wp – их взаимным расположением.
Из формулы следует, что работа консервативных
сил равна убыли потенциальной энергии:
dA dWp.
21.
Потенциальная энергия пригравитационном взаимодействии
Нет единого выражения для Wp. В разных
случаях она определяется по-разному.
Работа тела при падении
Или
A Wp Wp 0 .
A mgh.
Условились считать, что на поверхности
земли (h 0), Wp0 0
тогда Wp A т.е.
Wp mgh.
22.
Для случая гравитационного взаимодействиямежду массами M и m, находящимися на расстоянии r
друг от друга, потенциальную энергию можно найти
по формуле:
Mm
Wp
.
r
23.
24.
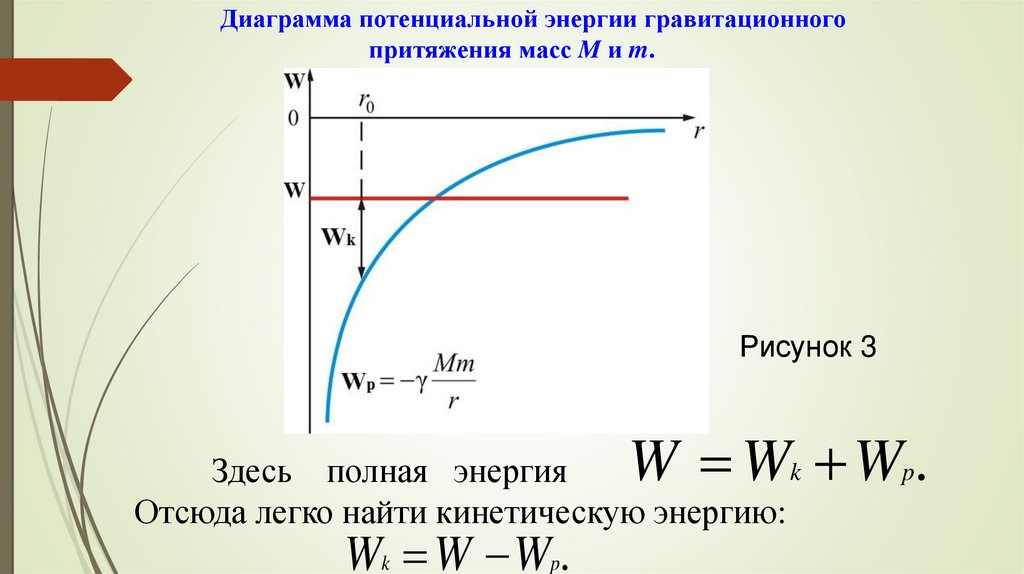
Диаграмма потенциальной энергии гравитационногопритяжения масс M и m.
Рисунок 3
W W Wp.
k
Здесь полная энергия
Отсюда легко найти кинетическую энергию:
Wk W Wp.
25.
Потенциальная энергия упругой деформации(пружины)
Найдём работу, совершаемую при
деформации упругой пружины.
Сила упругости Fупр kx,
Сила
непостоянна, поэтому элементарная работа
dA Fdx kxdx
знак минус говорит о том, что работа
совершена над пружиной.
kx kx
A dA kxdx
,
2
2
x2
x1
2
2
1
2
26.
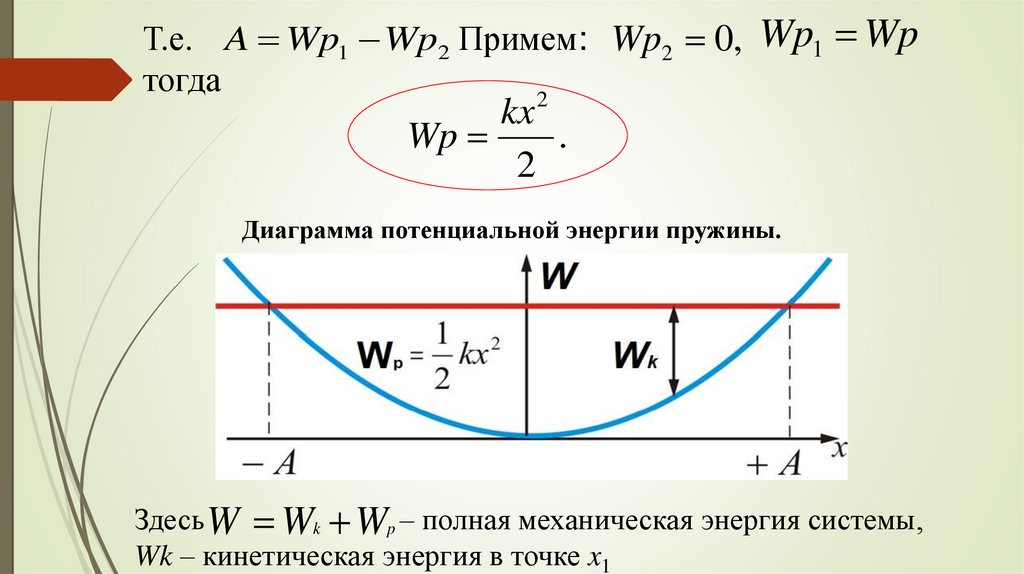
Т.е. A Wp1 Wp2 Примем: Wp2 0, Wp1 Wpтогда
2
kx
Wp
.
2
Диаграмма потенциальной энергии пружины.
Здесь W Wk Wp – полная механическая энергия системы,
Wk – кинетическая энергия в точке x1
27.
Связь между потенциальной энергией исилой
Пространство, в котором действуют
консервативные
силы,
называется
потенциальным полем.
Каждой точке потенциального поля
соответствует некоторое значение силы
F
действующей на тело, и некоторое значение
потенциальной энергии Wp.
Значит, между силой F и Wp должна быть
связь.
28.
Т.к. dA dWpс другой
стороны,
следовательно,
отсюда
dA Fd r
Fd r dWp
dWp
F .
dr
Проекции вектора силы на оси координат:
Wp
Wp
Wp
Fx
; Fy
; Fz
.
x
z
y
29.
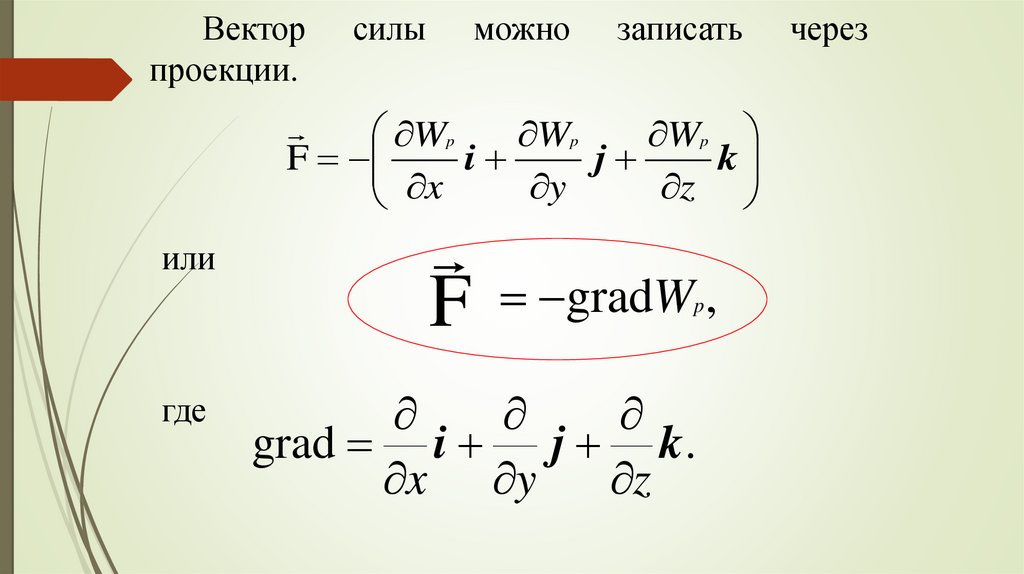
Векторпроекции.
силы
можно
записать
Wp
Wp
Wp
F
i
j
k
y
z
x
или
F gradW ,
p
где
grad i j k .
x y
z
через
30.
grad i j k .x y
z
Градиент – это вектор, показывающий
направление
наибыстрейшего
увеличения
функции.
Т.к. в формуле стоит знак «минус», то
F направлен в сторону наибыстрейшего
уменьшения Wp.
F gradWp,
31.
4. Закон сохранения энергии. Закон сохранения импульса.Закон сохранения сводит воедино результаты,
полученные нами раньше.
В сороковых годах девятнадцатого века трудами Р.
Майера, Г. Гельмгольца и Дж. Джоуля (все в разное
время и независимо друг от друга) был доказан закон
сохранения и превращения энергии.
32. Джоуль Джеймс Прескотт (1818 –1889) – английский физик, один из первооткрывателей закона сохранения энергии.
Первые уроки по физике ему давал Дж.Дальтон, под влиянием которого Джоуль начал свои
эксперименты.
Работы
посвящены
механике,
электромагнетизму, кинетической теории газов.
33.
34.
Рассмотрим систему, состоящую из Nчастиц.Силы
взаимодействия между частицами
(F ) - консервативные.
внутр.
Кроме внутренних сил на частицы действуют
внешние консервативные и неконсервативные
силы, т. е. рассматриваемая система частиц или тел
консервативна.
35.
Для консервативной системы частицполная энергия системы:
W Wk Wвнутр. Wвнеш. const
Для механической энергии закон сохранения
звучит так: полная механическая энергия консер-
вативной системы материальных
остаётся постоянной.
точек
36.
Для замкнутой системы,т.е. для системы на которую не действуют
внешние силы, можно записать:
W Wk Wвнутр. const
полная механическая энергия
замкнутой
системы
материальных
точек, между которыми действуют
только консервативные силы, остаётся
постоянной.
т.е.
37.
Если в замкнутой системе действуютнеконсервативные силы, то полная
механическая энергия системы не сохраняется
– частично она переходит в другие виды
энергии – неконсервативные.
Система, в которой механическая
энергия переходит в другие виды энергии,
называется диссипативной,
а сам процесс перехода называется
диссипацией энергии.
38.
В диссипативной, изолированной отвнешнего воздействия системе остаётся
постоянной сумма всех видов энергии
(механической, тепловой и т.д.) Здесь
действует общий закон сохранения энергии.
Этот процесс хорошо демонстрирует
маятник Максвелла. Роль консервативной
внешней силы здесь играет гравитационное
поле. Маятник прекращает свое движение из-за
наличия внутренних неконсервативных сил
(сил трения, сопротивления воздуха).
39.
40.
Максвелл Джеймс Клерк (1831 –1879) –
английский физик. Работы
посвящены
электродинамике,
молекулярной физике, общей
статике, оптике, механике, теории упругости.
Установил статистический закон, описывающий
распределение молекул газа по скоростям. Самым
большим достижением Максвелла является теория
электромагнитного
поля,
которую
он
сформулировал в виде системы нескольких
уравнений,
выражающих
все
основные
закономерности электромагнитных явлений.
41.
Закон сохранения импульса.Центр инерции или центр масс системы материальных
точек называют такую точку С (рисунок 4), радиус-вектор
которой:
1
m r
r
m r,
m
m
n
i 1
c
i
i
n
i 1
n
i 1
i
i
i
где m m – общая масса системы, n – число точек системы.
n
i 1
i
Рисунок 4
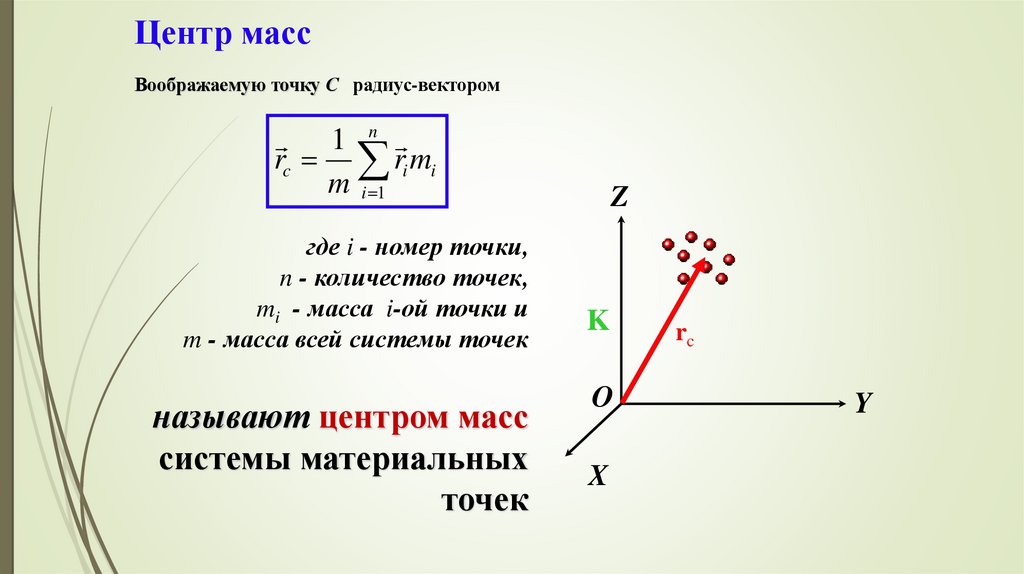
42. Центр масс
Воображаемую точку С радиус-вектором1 n
rc ri mi
m i 1
где i - номер точки,
n - количество точек,
mi - масса i-ой точки и
m - масса всей системы точек
называют центром масс
системы материальных
точек
Z
K
O
X
rc
Y
43.
При этом не надо путать центр масс сцентром тяжести системы – с точкой
приложения равнодействующей сил тяжести
всех тел системы.
Центр тяжести совпадает с центром
масс (центром инерции), если g (ускорение
силы тяжести) для всех тел системы
одинаково (когда размеры системы гораздо
меньше размеров Земли).
44.
Скорость центра инерции системыυc
n
n
d rc 1
d ri 1
υc
mi
mi υi.
dt m i 1 dt m i 1
n
p mi υi
i 1
– импульс системы тел, υ – скорость i-го тела системы. Так как
p
i
n
mi υi mυc
i 1
то импульс системы тел можно определить по формуле
p mυc
– импульс системы тел равен произведению массы системы на
скорость её центра инерции.
45. Закон сохранения импульса
Механическая система называется замкнутой (илиизолированной), если на неё не действуют внешние силы, т.е.
она не взаимодействует с внешними телами.
Строго говоря, каждая реальная система тел всегда не замкнута,
т.к. подвержена, как минимум воздействию гравитационных сил. Однако
если внутренние силы гораздо больше внешних, то такую систему
можно считать замкнутой (например – Солнечная система).
Для замкнутой системы равнодействующий вектор
внешних сил тождественно равен нулю:
dp
F 0,
dt
46.
nотсюда
p mi υc const.
i 1
Это есть закон сохранения импульса: импульс замкнутой
системы не изменяется во времени.
Импульс системы тел может быть представлен
в виде произведения
суммарной массы тел на скорость центра инерции: p m c , тогда
m c const.
При любых процессах, происходящих в замкнутых
системах, скорость центра инерции сохраняется неизменной.
Закон сохранения импульса является одним из основных законов
природы. Он был получен как следствие законов Ньютона, но он
справедлив и для микрочастиц и для релятивистских скоростей, когда
c
47.
48.
49.
Если системане замкнута,
но главный вектор
внешних сил F 0
то p сист. const,
как если бы внешних сил не было (например, прыжок из
лодки, выстрел из ружья или реактивное движение).
50.
51. Применение законов сохранения Абсолютно упругий центральный удар
При абсолютно неупругом ударе закон сохранениямеханической энергии не работает.
Применим закон сохранения механической энергии
для расчета скорости тел при абсолютно упругом ударе
– это такой удар, при котором не происходит
превращения механической энергии в другие виды
энергии.
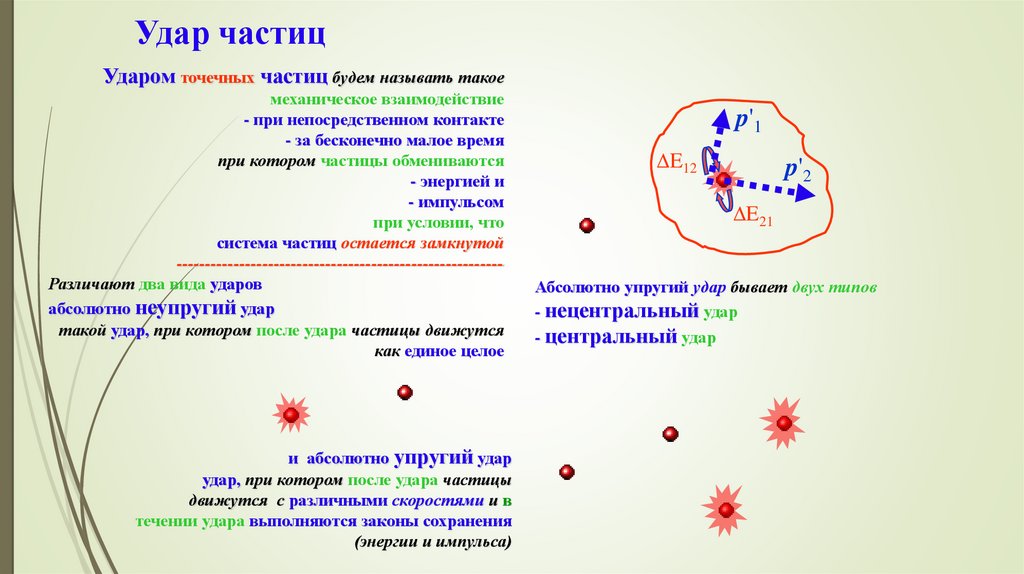
52. Удар частиц
Ударом точечных частиц будем называть такоемеханическое взаимодействие
- при непосредственном контакте
- за бесконечно малое время
при котором частицы обмениваются
- энергией и
- импульсом
при условии, что
система частиц остается замкнутой
--------------------------------------------------------Различают два вида ударов
абсолютно неупругий удар
такой удар, при котором после удара частицы движутся
как единое целое
и абсолютно упругий удар
удар, при котором после удара частицы
движутся с различными скоростями и в
течении удара выполняются законы сохранения
(энергии и импульса)
p'1
E12
p'2
E21
Абсолютно упругий удар бывает двух типов
- нецентральный удар
- центральный удар
53.
Пример 1. Абсолютно-упругий центральный ударРазберем на примере
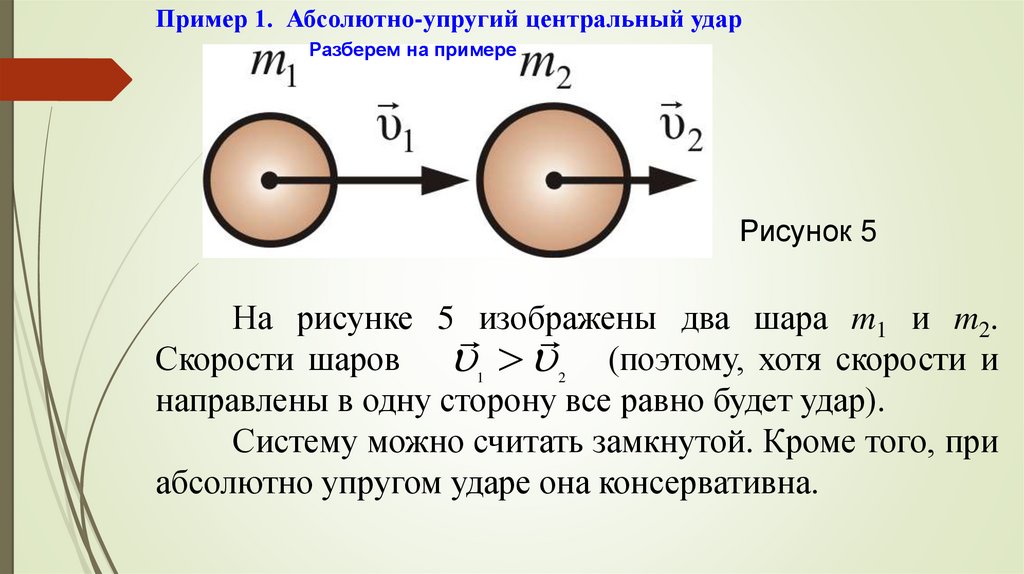
Рисунок 5
На рисунке 5 изображены
два шара m1 и m2.
Скорости шаров 1 2 (поэтому, хотя скорости и
направлены в одну сторону все равно будет удар).
Систему можно считать замкнутой. Кроме того, при
абсолютно упругом ударе она консервативна.
54.
Обозначим '1 и '2 – скорости шаров послеих столкновения.
В данном случае можно воспользоваться законом
сохранения механической энергии и законом
сохранения импульса (в проекциях на ось x):
m m m ' m '
2
2
2
2
m m m ' m '.
2
1
1
1
1
2
2
2
2
2
2
1
1
1
1
2
2
2
2
2
По ЗСЭ
По ЗСИ
55.
Решив эту систему уравнений относительно'1 и '2 получим
2m (m m )
'
;
m m
2
2
1
2
1
1
1
2
2m (m m )
'
m m
1
1
2
1
2
2
1
2
Таким образом, скорости шаров после абсолютно
упругого удара не могут быть одинаковыми по
величине и по направлению.






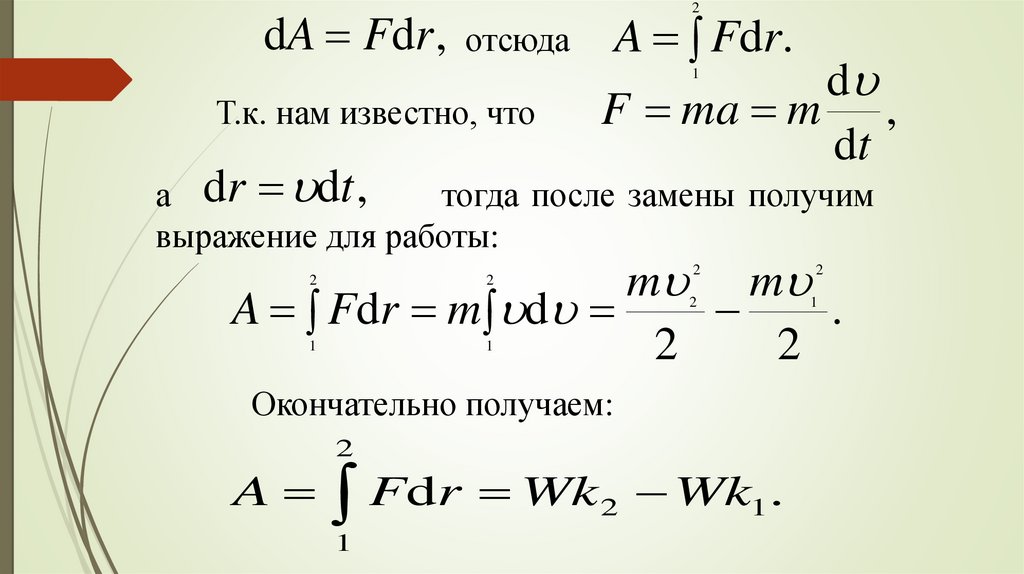





































 Физика
Физика








