Работа. Энергия. Законы сохранения в механике

1.

( В МЕХАНИКЕ )

2.

Элементарная работа А силы
F
при перемещении МТ на dr :
А
(
F
d
r
)
F
F 2 А Fdr cos F ds,
МТ
dr где - угол между F и dr ,
F F cos
1
и ds dr.

3.

Работа А1 2 силы на конечном
перемещении МТ из 1 в 2:
F
А1 2
1
F При действии на МТ
2 нескольких сил:
dr
1
F dr .
2
A F1 F2 ... dr
F1dr F2 dr ... A1 A2 ...

4.

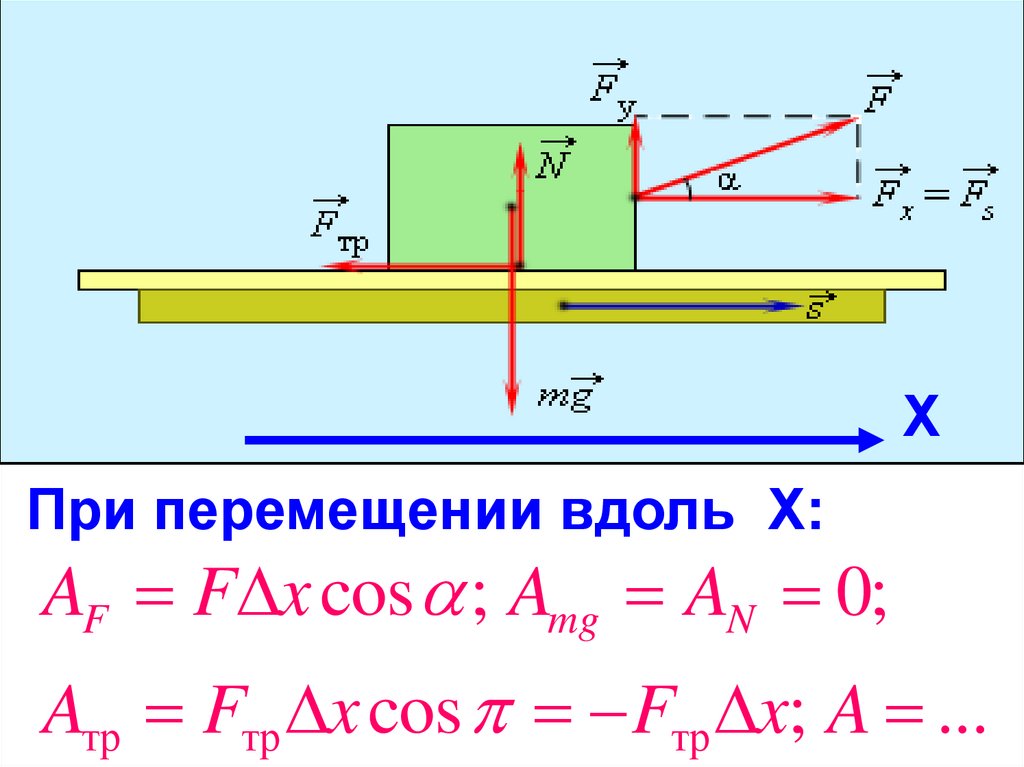
Х
При перемещении вдоль Х:
AF F x cos ; Amg AN 0;
Aтр Fтр x cos Fтр x; A ...

5.

Мощность
Характеризует работу, совершаемую силой за единицу времени:
A dr Дж
м
N
F
F ,
Н Вт
dt
dt
с
с
где - скорость перемещения
точки приложения силы.
Работа и мощность силы зависят
от выбора системы отсчета.

6.

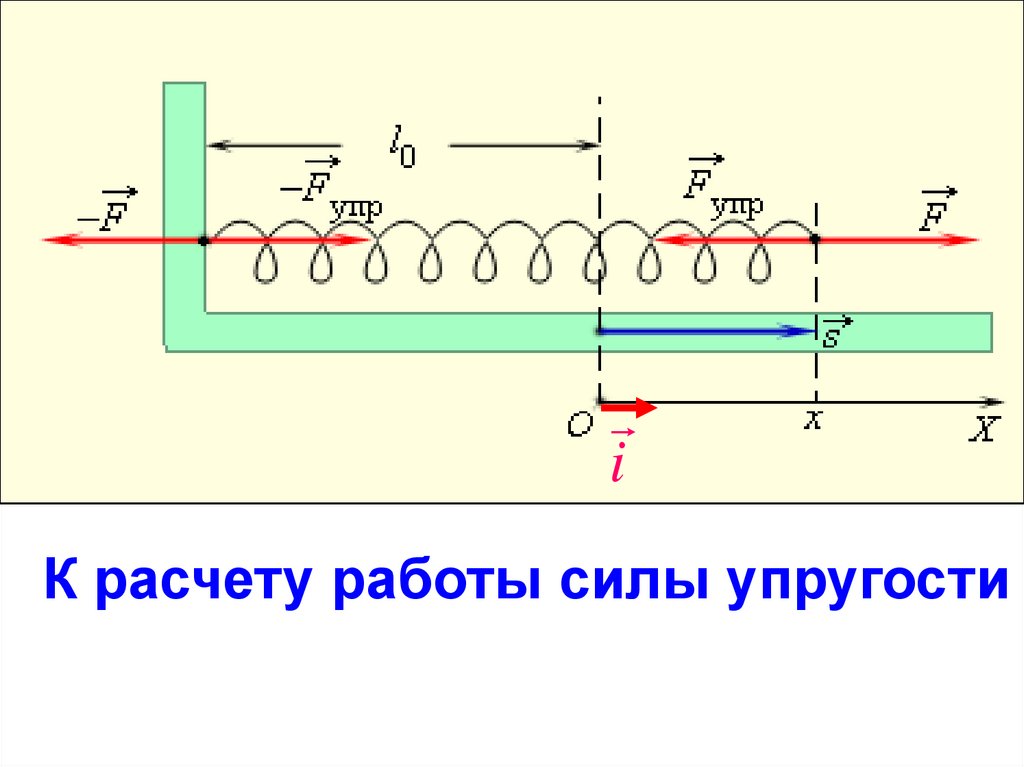
i
К расчету работы силы упругости

7.

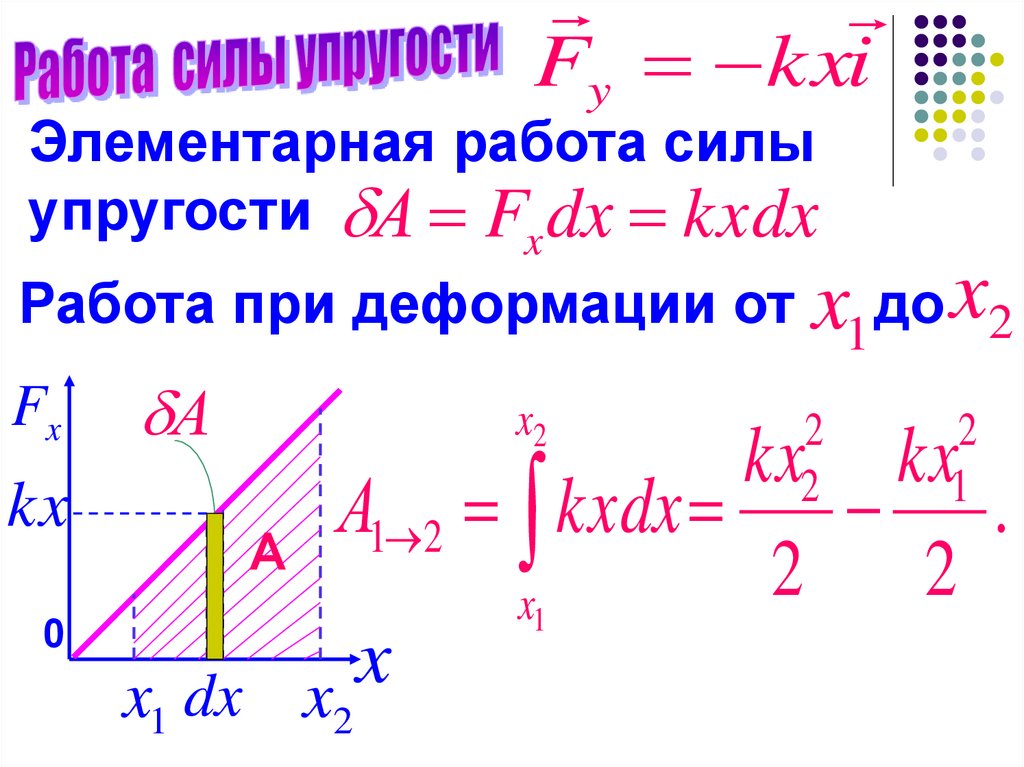
Fy kxi
Элементарная работа силы
упругости А Fx dx kxdx
Работа при деформации от x1 до x2
Fx А
x2
2
2
kx2 kx1
kx
А
kxdx
.
1 2
x
А
2
2
1
0
x
x1 dx x2

8.

Зависит от положения
начальной и конечной точек.
Сила упругости –
консервативная сила.
Для консервативных сил работа
по замкнутому
контуру
равна
нулю: Fd 0.
L
Консервативны сила тяготения,
упругости, кулоновская сила.

9.

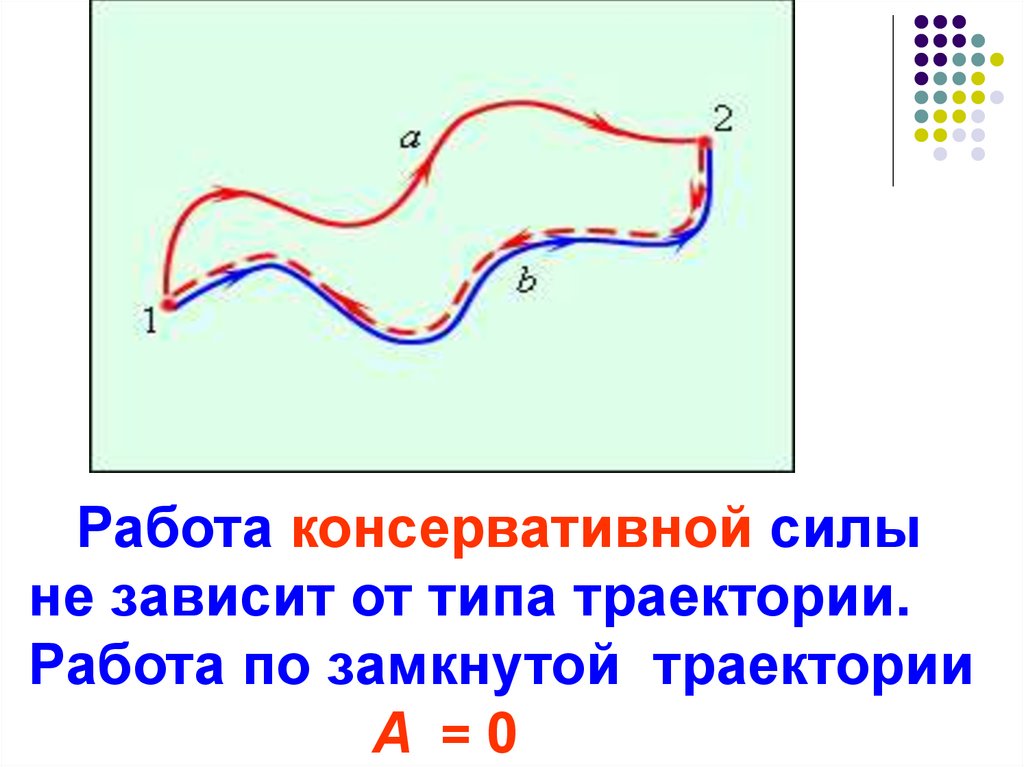
Работа консервативной силы
не зависит от типа траектории.
Работа по замкнутой траектории
A =0

10.

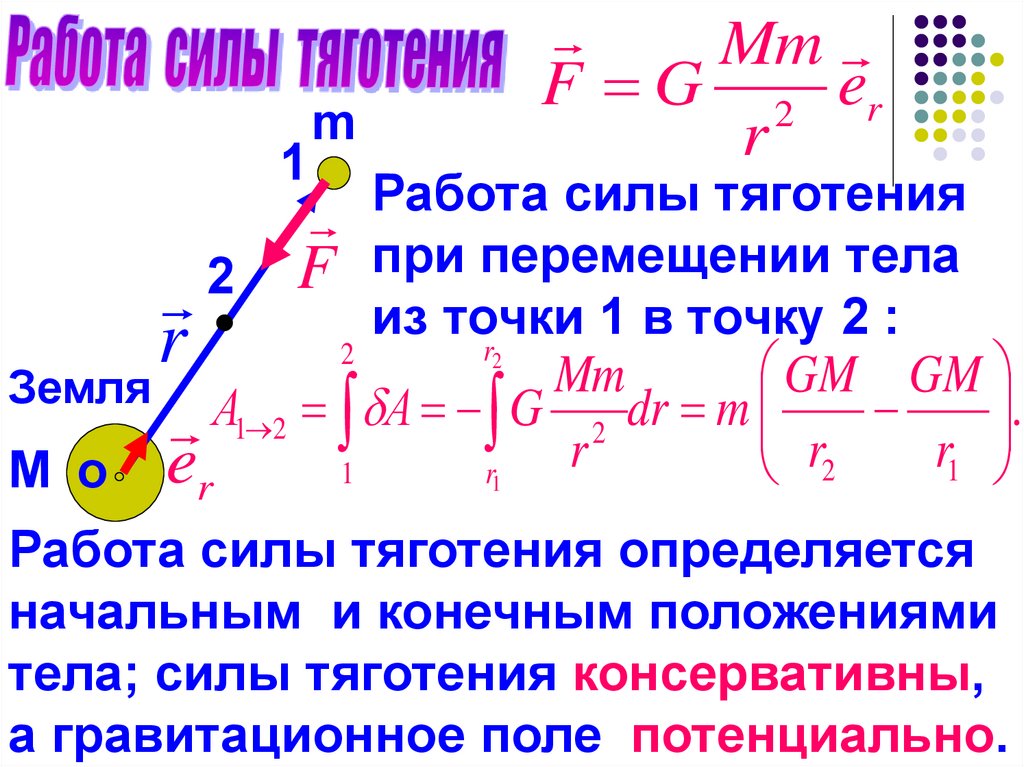
1
m
Mm
F G 2 er
r
Работа
силы
тяготения
при
перемещении
тела
F
2
из точки 1 в точку 2 :
r2
r
2
Земля А А G Mm dr m GM GM .
1 2
2
r
r1
r2
1
r1
М о e
r
Работа силы тяготения определяется
начальным и конечным положениями
тела; силы тяготения консервативны,
а гравитационное поле потенциально.

11.

Диссипативные силы те,
работа которых зависит от
траектории перемещения тела
из одной точки в другую.
Это силы трения, внутреннего
трения, сопротивления.

12.

При вращении тела вокруг неподвижной оси вращательный момент
создает сила F , касательная к
траектории движения точки ее
приложения .
Работа A силы
на угол d :
F
при повороте
A F ds F rd M z d ,
где
F
MZ
- проекция момента силы
на ось Z.

13.

При M z const для
поворота на угол
совершается работа:
A M z d M z
0
M z d .
В общем случае:
A M d Md cos .

14.

ВНИМАНИЕ!
Для механической энергии используются разные обозначения:
Кинетическая энергия -
K , Т , WК , ЕК ;
Потенциальная энергия –
П , W р , Wn , E р .

15.

Кинетическая энергия
механической системы –
энергия ее механического
движения .
Энергия движущегося тела возрастает на величину затраченной работы dWк А.
Учтем, что
А
F
d
r
,
d
и dr dt ,
а F m
dt
получим
dWк m d .

16.

Тело массой m , движущееся
со скоростью c имеет
кинетическую энергию :
2
m
Wк m d
.
2
0
Изменение кинетической энергии
WK 0 увеличивается при A 0;
WK 0 уменьшаетс я при A 0.

17.

Кинетическая энергия
вращающегося твердого тела
(ось Z неподвижна).
Кинетическая энергия dWК
элемента массы dm ,
отстоящего от оси Z на
расстоянии r :
1 2
1 2 2
dWК dm r dm.
2
2 2

18.

Кинетическая энергия
вращающегося ТТ, ось Z
неподвижна:
2
1
2
WК
r
dm
J
;
z
2 m
2
2
J Z
WK
.
2
2

19.

При произвольном движении ТТ W
К
равна сумме кинетической энергии
поступательного движения со
скоростью c его центра масс и
кинетической энергии вращения тела с
угловой скоростью
вокруг
мгновенной оси, проходящей через
центр масс : W W пост W вращ,
К
К
К
1
1
2
2
WК m c J c ,
2
2
если J c const.

20.

Потенциальная энергия –
механическая энергия системы
тел, определяется взаимным
расположением тел и характером их взаимодействия .
Работа в поле консервативных
сил совершается за счет убыли
потенциальной энергии :
A dWp
или
dWp Fdr .

21.

Потенциальная энергия
определяется с точностью до
произвольной постоянной :
W p Fdr C ,
C – зависит от выбора
начальных условий.
В задаче выбирают «нулевую конфигурацию» системы, в которой
W p 0.

22.

Для консервативных сил выполняются соотношения :
W p
Wp
W p
Fx
, Fy
, Fz
.
x
y
z
Или в векторном виде :
W p W p W p
F
i
j
k W p ,
y
z
x
где i
j k - оператор Гами x
y
z льтона (набла)
Или так:
F grad Wp ,

23.

т.е. сила, действующая на МТ в
потенциальном поле, равна
взятому с обратным знаком
градиенту потенциальной
энергии этой МТ в данном поле.
Вид функции W p зависит от характера силового поля. W p системы
определяется ее конфигурацией.

24.

Потенциальная энергия
определяется с точностью до
произвольной постоянной :
W p Fdr C ,
C – зависит от выбора
начальных условий.
В задаче выбирают «нулевую
конфигурацию» системы, в
которой W p 0.

25.

Законы сохранения
в механике
- фундаментальные законы
природы:
1)закон сохранения импульса(ЗСИ);
2) закон сохранения момента
импульса (ЗСМИ);
3) закон сохранения механической
энергии (ЗСМЭ).

26.

(ЗСИ)
Фундаментальный закон
природы - следствие
однородности пространства.

27.

проявляется в том, что законы
движения и физические
свойства замкнутой системы не
зависят от выбора начала
координат ИСО (не изменяются, если замкнутую систему
перемещать в пространстве как
целое путем параллельного
переноса).

28.

З С И:
Импульс замкнутой системы
взаимодействующих МТ с
течением времени
не изменяется
dр
0
dt
или
p pi mi i const ,
n
n
i 1
i 1
где mi , i - масса и скорость
i -той МТ.

29.

главный
вектор
внешних сил равен
нулю
F
0,
проекция главного вектора внешних
сил на неподвижную ось равна нулю
внеш
внеш
( F ) x, y , z 0,
внутренние
силы значительно
превышают внешние силы
F
внутр
F
внеш
.

30.

Закон сохранения момента
импульса
ЗСМИ – фундаментальный закон
природы – следствие изотропности пространства: физические законы инвариантны относительно
поворота замкнутой системы в
пространстве на любой угол.

31.

dLZ
0,
dt
LZ const
- момент импульса замкнутой
системы тел относительно
неподвижной оси сохраняется,
т.е. не изменяется с течением
времени.

32.

ЗСМИ выполняется и в незамкнутой системе, если относительно
неподвижной оси суммарный
момент внешних сил равен нулю
внеш
M z 0.

33.

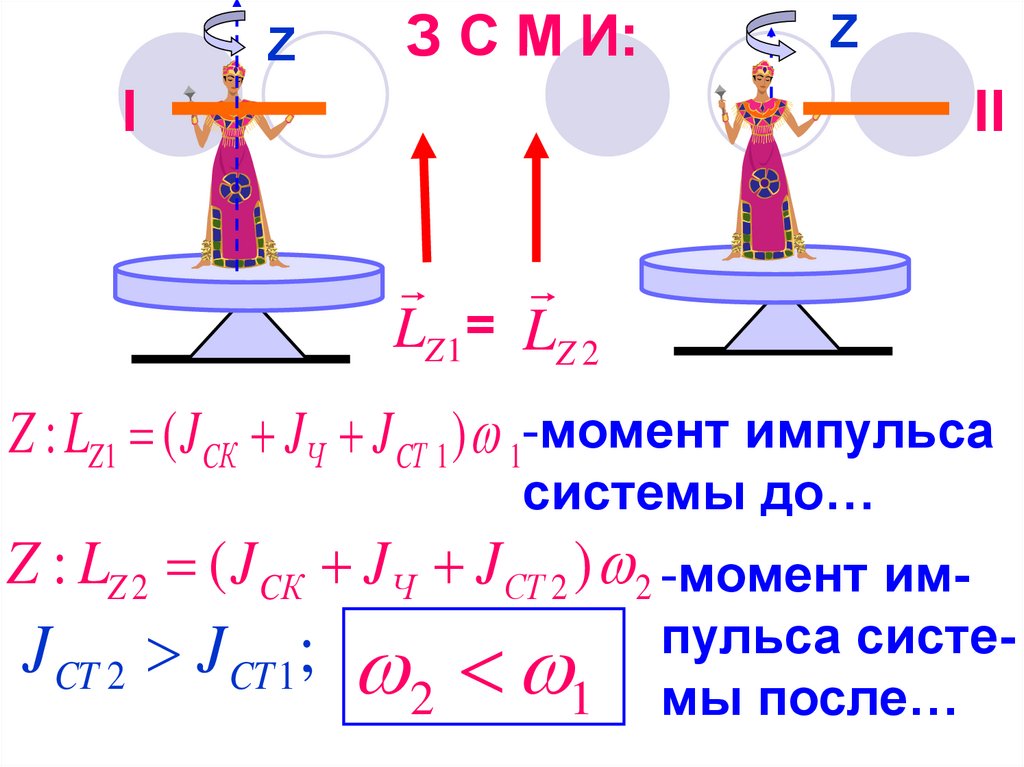
Z
З С М И:
Z
I
II
LZ 1 = LZ 2
Z : LZ1 ( J CК JЧ J CТ 1 ) 1-момент импульса
системы до…
Z : LZ 2 ( J CК JЧ J СТ 2 ) 2 -момент им-
J CT 2 J CT 1;
2 1
пульса системы после…

34.

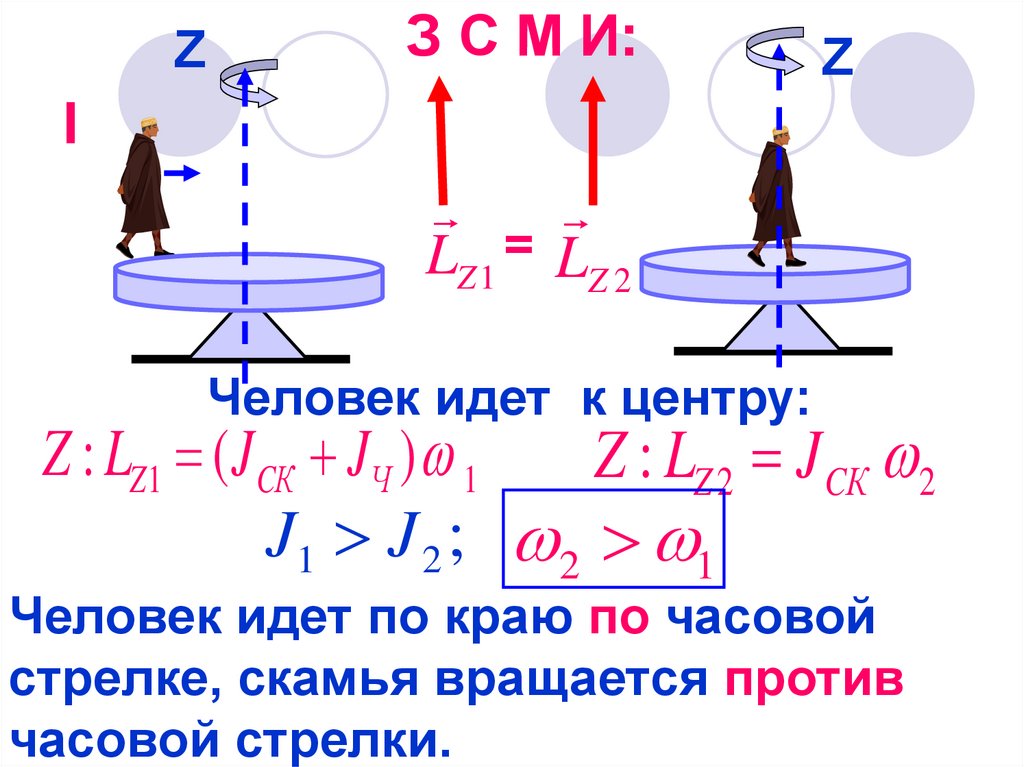
Z
З С М И:
Z
I
LZ 1 = LZ 2
Человек идет к центру:
Z : LZ1 ( J CК JЧ ) 1
Z : LZ 2 J CК 2
J1 J 2 ; 2 1
Человек идет по краю по часовой
стрелке, скамья вращается против
часовой стрелки.

35.

Механическая энергия консервативной системы с течением
времени не изменяется:
Wк W p const.
ЗСМЭ связан с однородностью
времени, которая проявляется в том,
что законы движения замкнутой системы не зависят от выбора начала
отсчета времени.

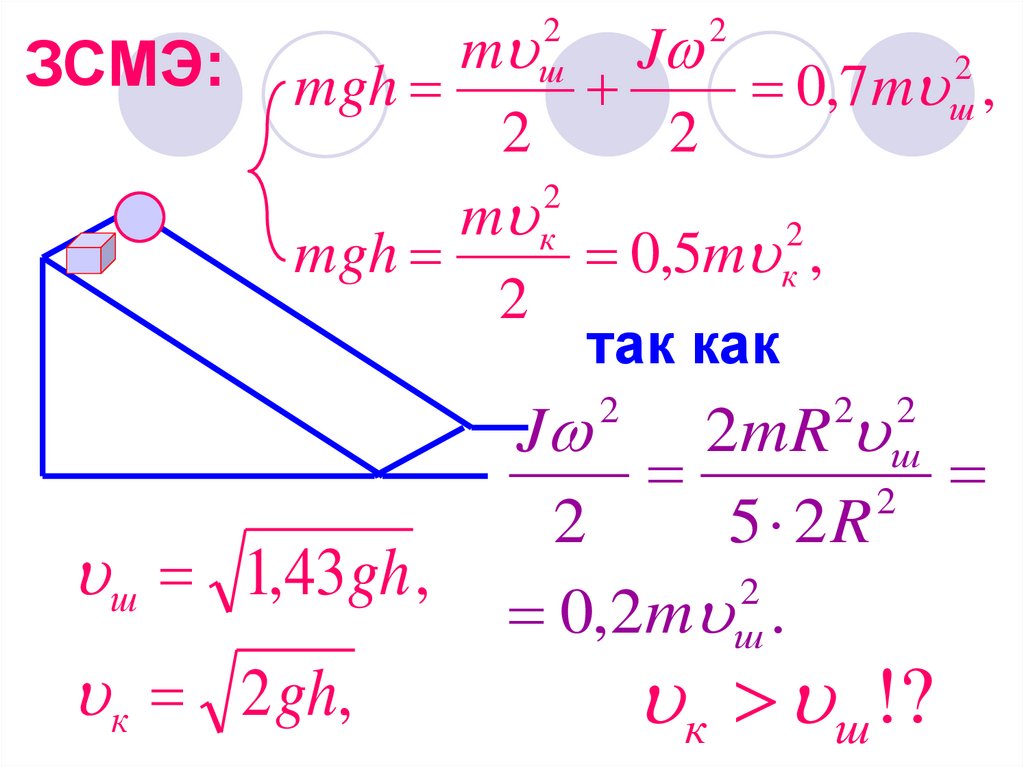
36.

Задача. Сравнить скорости
движения куба и шара у
основания наклонной
плоскости (массы одинаковы,
трением пренебречь).

37.

ЗСМЭ:
m
J
2
mgh
0,7m ш ,
2
2
2
m к
2
mgh
0,5m к ,
2
так как
2
ш
2
2mR
J
2
5 2R
2
0,2m ш .
2
ш 1,43gh ,
к 2 gh,
2
2
ш
2
к ш !?

38.

Аналогия соотношений поступательного и вращательного
движения

39.

С
Р
А
В
Н
И,
З
А
П
О
М
Н
И
МЕХАНИКА
( основные
понятия
и
законы
)
d
dr
dt
dt
d
d
a
dt
dt
Jz
m
p; p m L, Lz , Lz ; Lz J z
M,Mz,Mz
F

40.

С
dp
d
L
z
Р F ma , F
M
J
,
M
z
z
z
А
n
dt
dt
n
В
Н mi i const
J zi i const
i 1
И, i 1
З
А
П
О
М
Н
И
- для замкнутой
системы.
A Fdr
2
m
WK
2
A M z d
2
J z
WK
2
m
J z
- тело катится.
WK
2
2
2
2

41.

СИТ - 3
[1] §15
Удар абсолютно упругих
и неупругих тел
Примечание: Рис. 18 – 22
расположить по тексту