Презентация_по_теме_Тригонометрические_неравенства

1. Решение простейших тригонометрических неравенств

2. Определение

Тригонометрическими неравенствами
называются неравенства, которые
содержат переменную под
знаком тригонометрической функции
неравенства cost >a,
cost ≥ a, cost <a, cost ≤ a
неравенства sint >a,
sint ≥ a, sint <a, sint ≤ a

3. Неравенство sint>a

01
Неравенство
sint>a

4. Неравенство sint > a Алгоритм решения

Неравенство sint > a
Алгоритм решения
y
1
t1
π-t1
a
0
-1
x
1. Отметить на оси ординат
интервал y > a.
2.Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать положительный обход
дуги ( против часовой стрелки)
4.Записать числовые значения
граничных точек, при этом начало
дуги- меньшее значение
5. Записать общее решение
неравенства.

5.

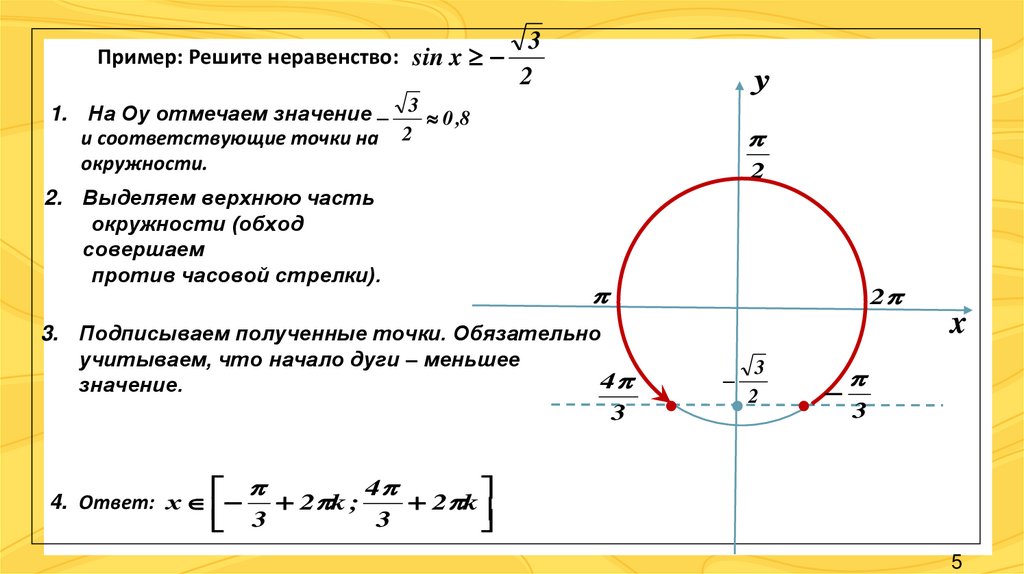
Пример: Решите неравенство: sin x
3
2
y
1. На Оу отмечаем значение 3 0 ,8
и соответствующие точки на 2
окружности.
2. Выделяем верхнюю часть
окружности (обход
совершаем
против часовой стрелки).
2
2
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее
4
значение.
3
4. Ответ: х
3
2 k ;
x
3
2
3
4
2 k
3
5

6. Неравество sint ≤ a

02
Неравество
sint ≤ a

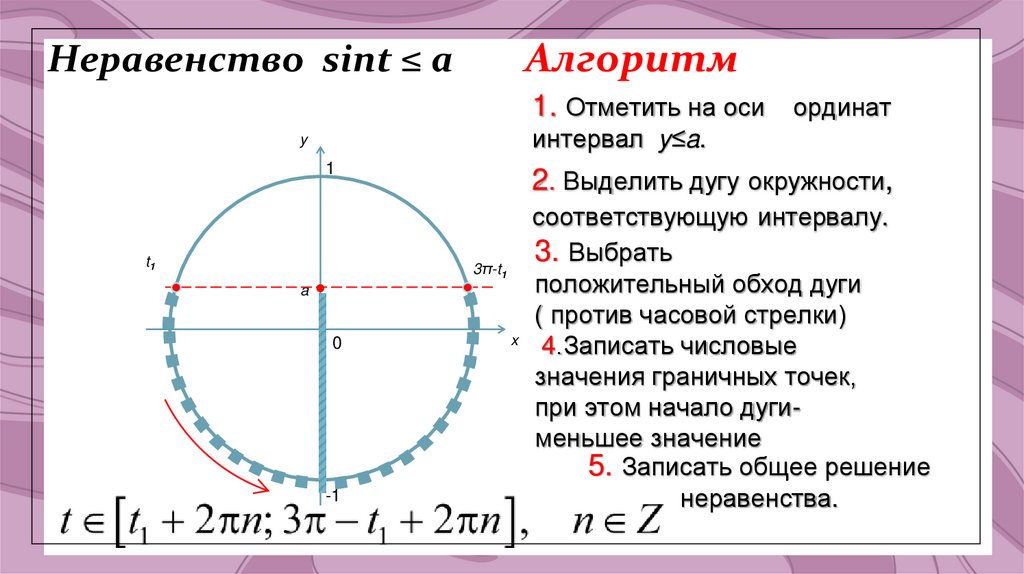
7. Неравенство sint ≤ a Алгоритм

Алгоритм
Неравенство sint ≤ a
1. Отметить на оси ординат
интервал y≤a.
y
1
t1
2. Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать
3π-t
положительный обход дуги
( против часовой стрелки)
x
4.Записать числовые
значения граничных точек,
при этом начало дугименьшее значение
5. Записать общее решение
неравенства.
1
a
0
-1

8.

y
2
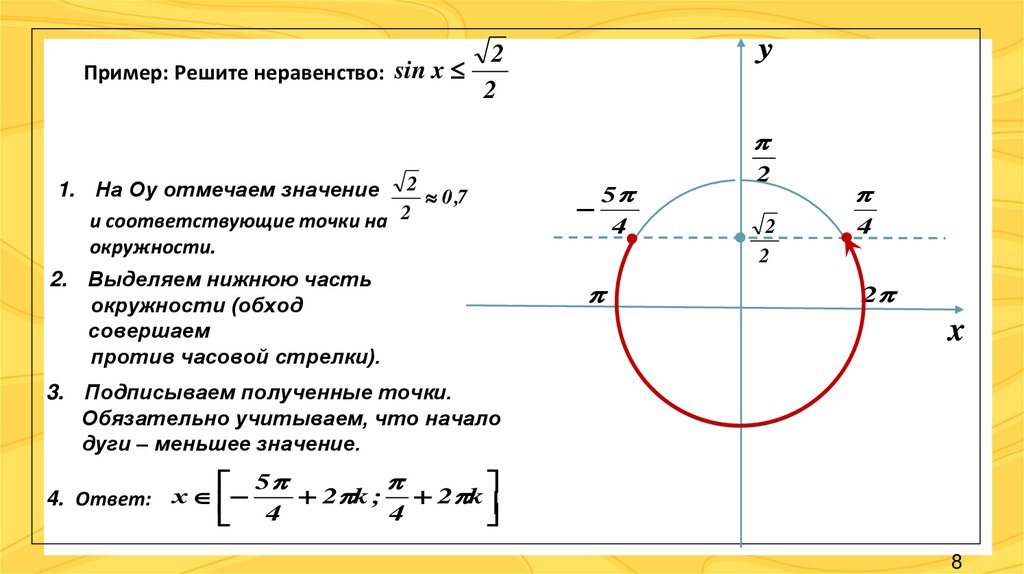
Пример: Решите неравенство: sin x
2
1. На Оу отмечаем значение 2 0 ,7
и соответствующие точки на 2
окружности.
5
4
2. Выделяем нижнюю часть
окружности (обход
совершаем
против часовой стрелки).
2
2
2
4
2
x
3. Подписываем полученные точки.
Обязательно учитываем, что начало
дуги – меньшее значение.
5
2 k ; 2 k
4. Ответ: х
4
4
8

9. Неравество cost > a

03
Неравество
cost > a

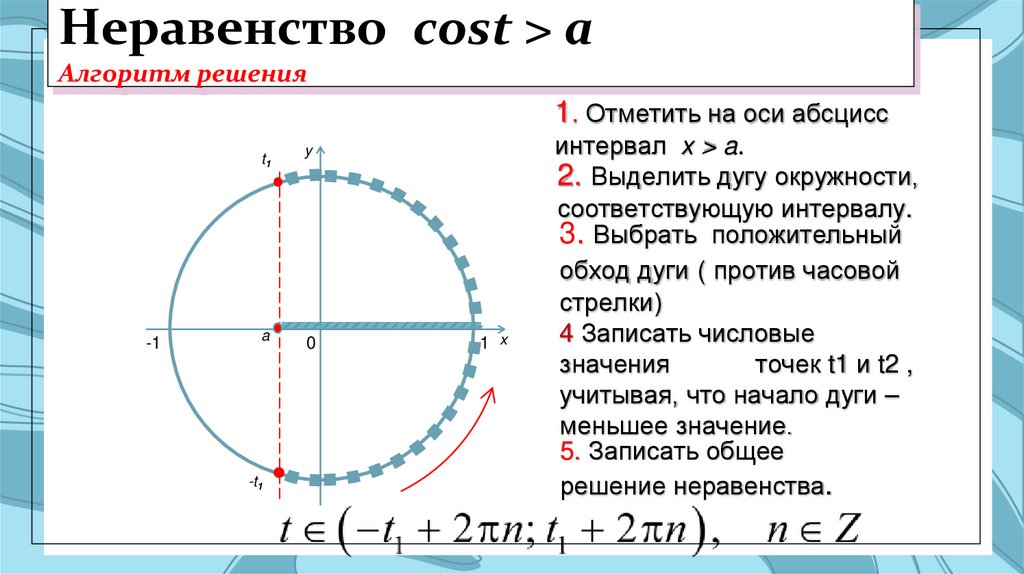
10. Неравенство cost > a Алгоритм решения

Неравенство cost > a
Алгоритм решения
1. Отметить на оси абсцисс
t1
-1
a
-t1
y
0
1 x
интервал x > a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать положительный
обход дуги ( против часовой
стрелки)
4 Записать числовые
значения
точек t1 и t2 ,
учитывая, что начало дуги –
меньшее значение.
5. Записать общее
решение неравенства.

11.

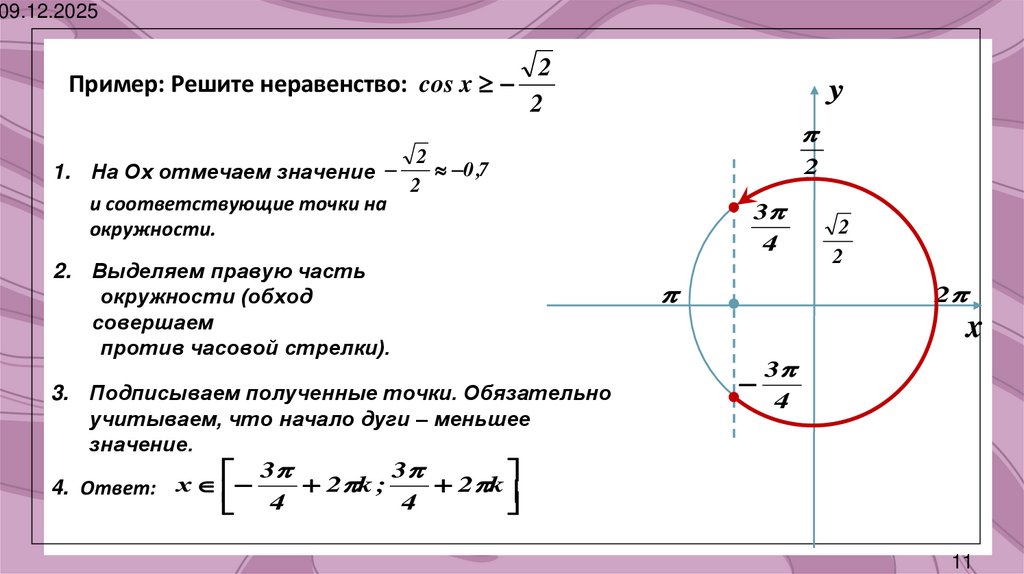
09.12.2025
Пример: Решите неравенство: cos x
2
2
y
2
0 ,7
1. На Ох отмечаем значение
2
и соответствующие точки на
окружности.
2. Выделяем правую часть
окружности (обход
совершаем
против часовой стрелки).
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее
значение.
4. Ответ: х
2
3
4
2
2
2
x
3
4
3
3
2 k ;
2 k
4
4
11

12. Неравество cost ≤ a

04
Неравество
cost ≤ a

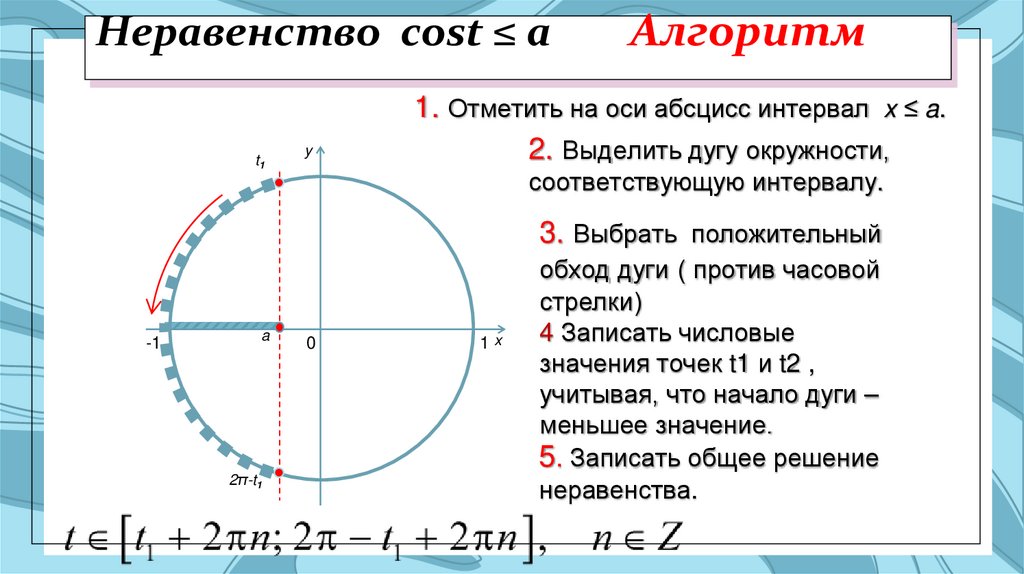
13. Неравенство cost ≤ a Алгоритм

Неравенство cost ≤ a
t1
y
Алгоритм
1. Отметить на оси абсцисс интервал x ≤ a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать положительный
-1
a
2π-t1
0
1x
обход дуги ( против часовой
стрелки)
4 Записать числовые
значения точек t1 и t2 ,
учитывая, что начало дуги –
меньшее значение.
5. Записать общее решение
неравенства.

14.

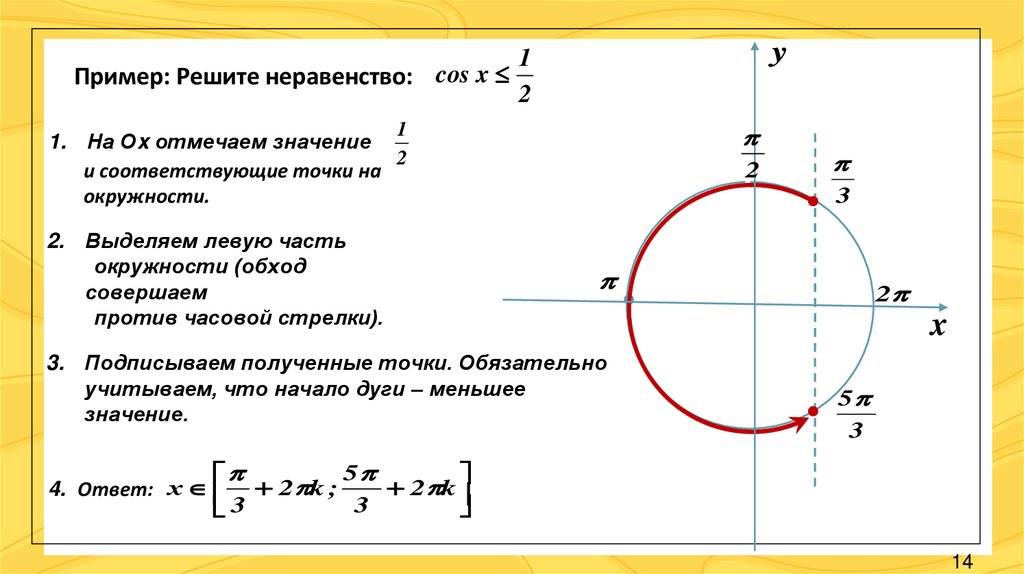
Пример: Решите неравенство: cos x
y
1
2
1
1. На Оx отмечаем значение
2
и соответствующие точки на
окружности.
2. Выделяем левую часть
окружности (обход
совершаем
против часовой стрелки).
2
3
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее
значение.
2
x
5
3
5
2 k
4. Ответ: х 2 k ;
3
3
14