L_211

1.

Правило Лопиталя применяется для случая
∞/∞ и 0/0
f ( x)
f ( x)
lim
lim
A
x a g ( x)
x a g ( x )
пропустить 1.5 страниц

2.

Не конспектировать! Только ознакомиться. Запишем на лекции
§ 4. Формула Тейлора и Маклорена
Опр. Многочленом (полиномом) n - го порядка называется функция
Pn ( x ) = a0 + a1 x + a2 x 2 + … + an x n
где a0 , a1 , …, an – числа – коэффициенты многочлена, n∈N .
Многочлен полностью определяется своими коэффициентами.
Опр. Многочленом (полиномом) по степеням (x – x0) называется выражение
Pn ( x ) = a0 + a1.( x – x0 ) + a2.( x – x0 ) 2+ … + an.( x – x0 ) n
пропустить 1 страницу

3.

Не конспектировать! Только ознакомиться. Запишем на лекции
Теорема
f ( x ) определена на интервале (a, b), имеет в точке
x∈(a, b) производные до n - го порядка включительно. Тогда при x → x0
функция f(x) будет сходится к своему многочлену Тейлора и можно записать
( n)
f ( x0 )
f
( x0 )
P( x) f ( x0 ) f ( x0 )( x x0 )
( x x0 )2 ...
( x x0 )n (2)
2!
n!
Выражение (1) называется многочленом Тейлора для функции f ( x )
Пусть функция
пропустить 25 клеточек
Теорема
f ( x ) и ее многочленом Тейлора P ( x ) является
б.м. величиной высшего порядка малости чем ( x – x0 )n
Разность между функцией
f (x) – P (x) = Rn(x) = o ((x – x0)n )
пропустить 25 клеточек
В форме Пеано
Rn(x) - остаточный член

4.

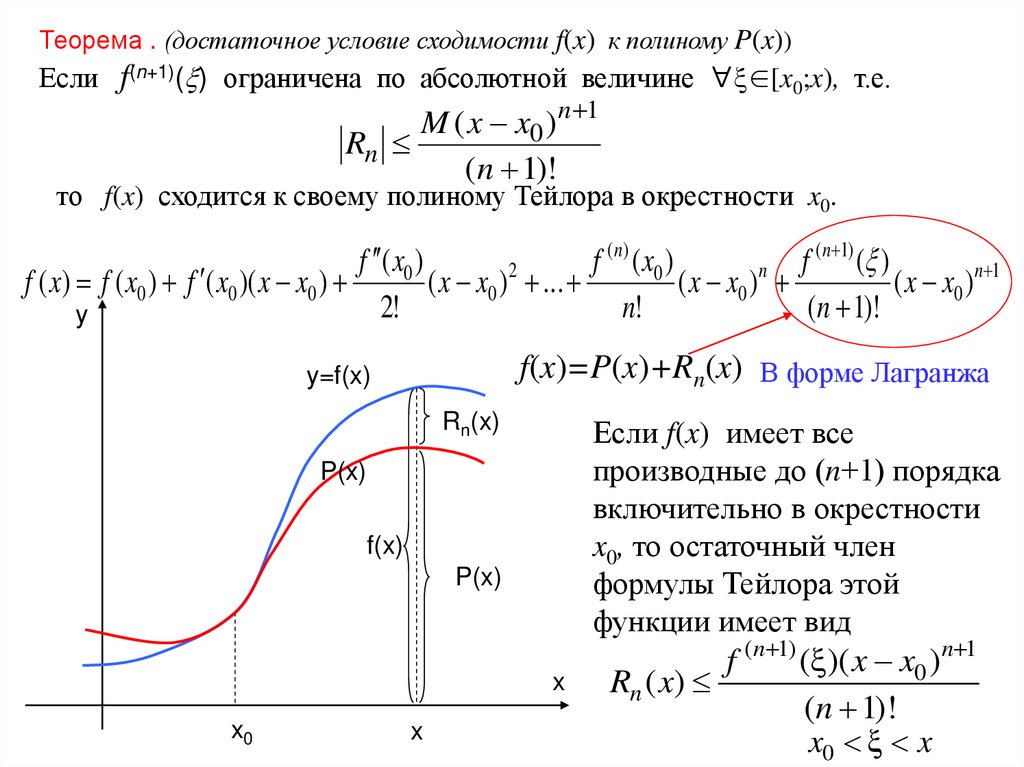
Теорема . (достаточное условие сходимости f(x) к полиному P(x))
Если f(n+1)( ) ограничена по абсолютной величине ∀ ∈[x0;x), т.е.
M ( x x0 ) n 1
Rn
(n 1)!
то f(x) сходится к своему полиному Тейлора в окрестности x0.
f ( x0 )
f ( n ) ( x0 )
f ( n 1) ( )
2
n
f ( x) f ( x0 ) f ( x0 )( x x0 )
( x x0 ) ...
( x x0 )
( x x0 )n 1
2!
n!
(n 1)!
y
f(x)=P(x)+Rn(x) В форме Лагранжа
y=f(x)
Rn(x)
Если f(x) имеет все
производные до (n+1) порядка
включительно в окрестности
x0, то остаточный член
формулы Тейлора этой
функции имеет вид
P(x)
f(x)
P(x)
x
x0
x
f ( n 1) ( )( x x0 )n 1
Rn ( x)
(n 1)!
x0 x

5.

Пример. Пусть
f(x) = sin x,
x0 = 0
y
sinx
-π
0
π