12_PrPl_25

1. DESKRIPTÍVNA GEOMETRIA

Prednáška 12
Obsah
ROTAČNÉ PLOCHY
rotačné plochy 2. stupňa a ich rezy
PRIAMKOVÉ PLOCHY
Základné vlastnosti
Rozdelenie
Nerozvinuteľné priamkové plochy
jednodielny hyperboloid
cylindroidy
konusoidy

2.

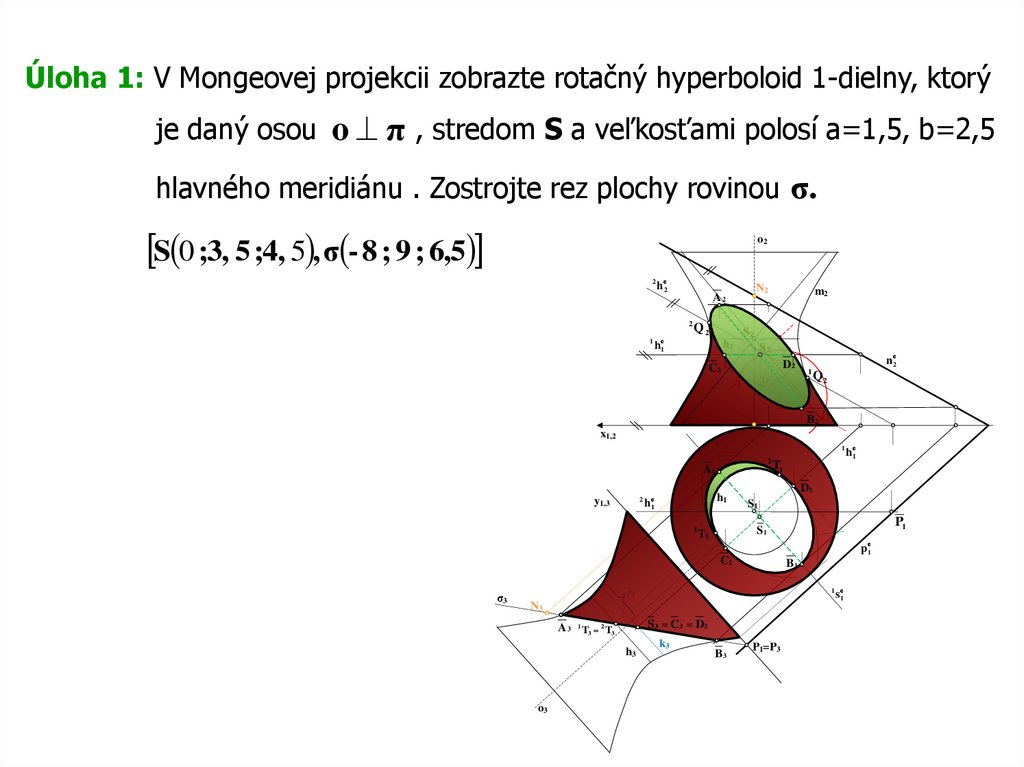
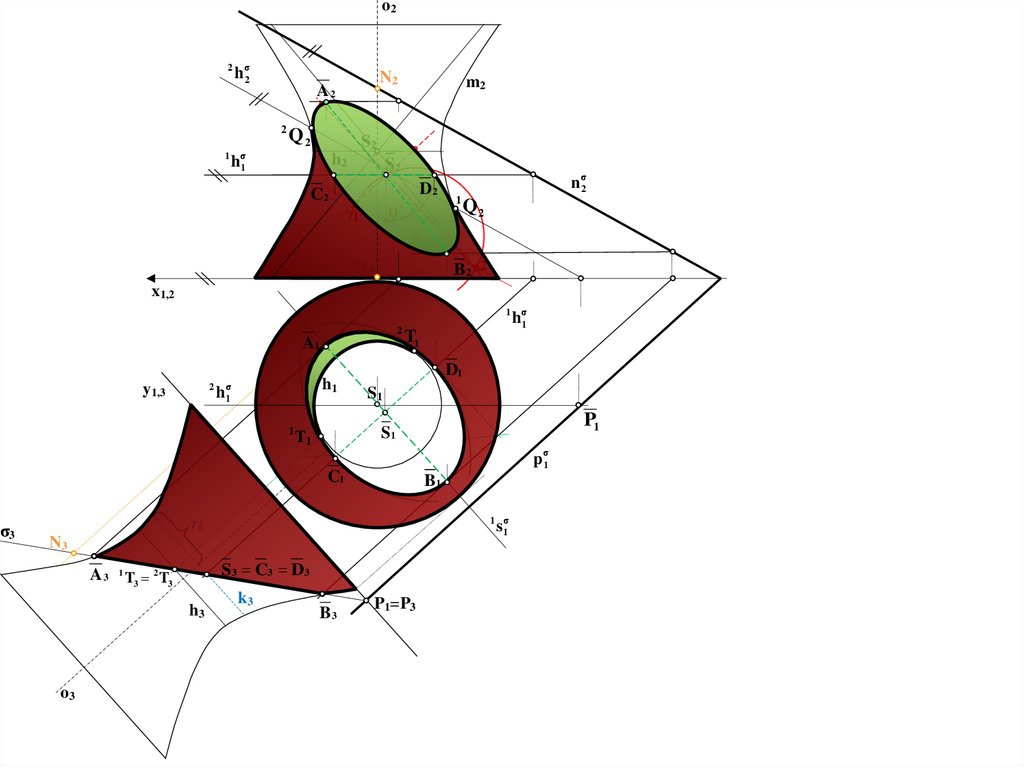
Úloha 1: V Mongeovej projekcii zobrazte rotačný hyperboloid 1-dielny, ktorý
je daný osou o π , stredom S a veľkosťami polosí a=1,5, b=2,5
hlavného meridiánu . Zostrojte rez plochy rovinou σ.
S 0 ;3, 5 ;4, 5 , σ - 8 ; 9 ; 6,5
o2
2
h σ2
2
1
h
N2
A2
Q2
m2
S2
σ
1
h2
S2
D2
C2
D
1
*
n σ2
1
Q2
Ω
N1
B2 2
x1,2
1
2
A1
y1,3
2
h1
h 1σ
1
D1
S1
P1
S1
T1
C1
σ3
1 σ
1
rk
s
S3 C3 D3
h3
o3
p1σ
k1 B 1
N3
A 3 1 T3 2 T3
k3
h1σ
T1
B3
P1=P3

3.

o22
2
h σ2
2
1
h
N22
A2
Q2
m22
S22
σ
1
h22
S2
D2
C2
D*
1
n σ2σ2
1
Q2
Ω
N11
B2 2
x1,2
1,2
1
2
A1
y1,3
1,3
2
h11
h 1σ
1
T1
D1
S11
P1
S1
T1
C1
σ33
1 σ
1
s
N33
S3 C3 D3
h33
o33
p1σ
k1 B 1
rk
A 33 1 T3 2ST3
k3
P2
h1σ
B33
P11=P33

4.

PRIAMKOVÉ PLOCHY
Definícia
Priamkovou plochou nazývame plochu, pre ktorú platí, že
každým jej bodom prechádza aspoň jedna priamka, ktorá celá
leží na ploche.

5.

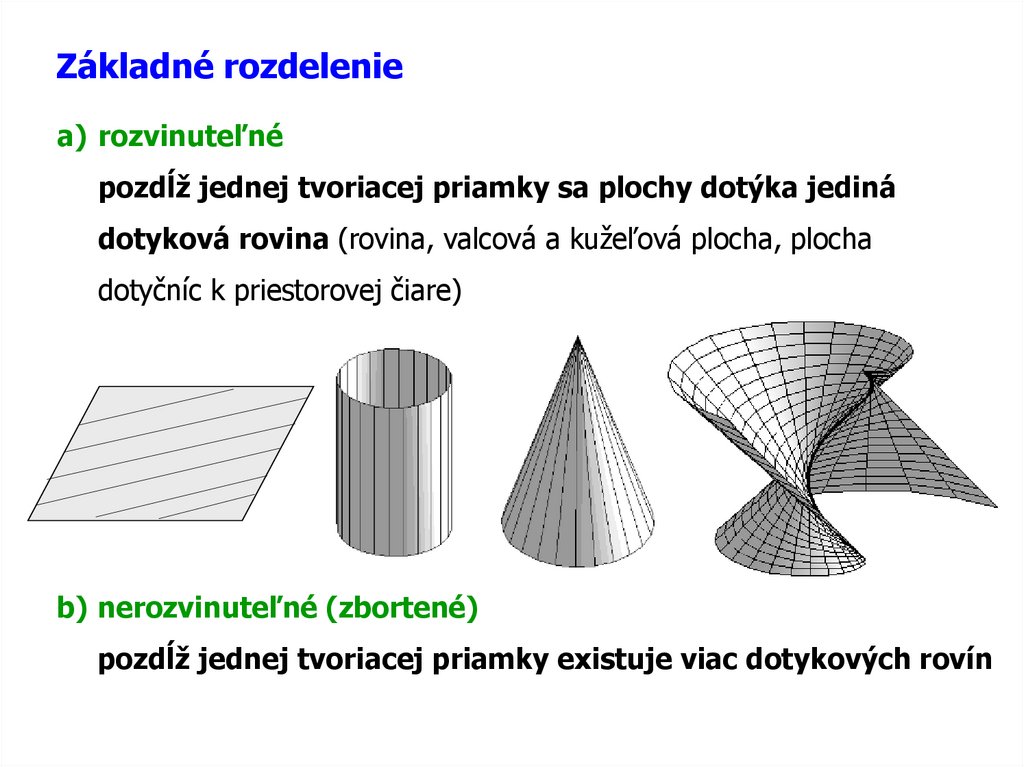
Základné rozdelenie
a) rozvinuteľné
pozdĺž jednej tvoriacej priamky sa plochy dotýka jediná
dotyková rovina (rovina, valcová a kužeľová plocha, plocha
dotyčníc k priestorovej čiare)
b) nerozvinuteľné (zbortené)
pozdĺž jednej tvoriacej priamky existuje viac dotykových rovín

6.

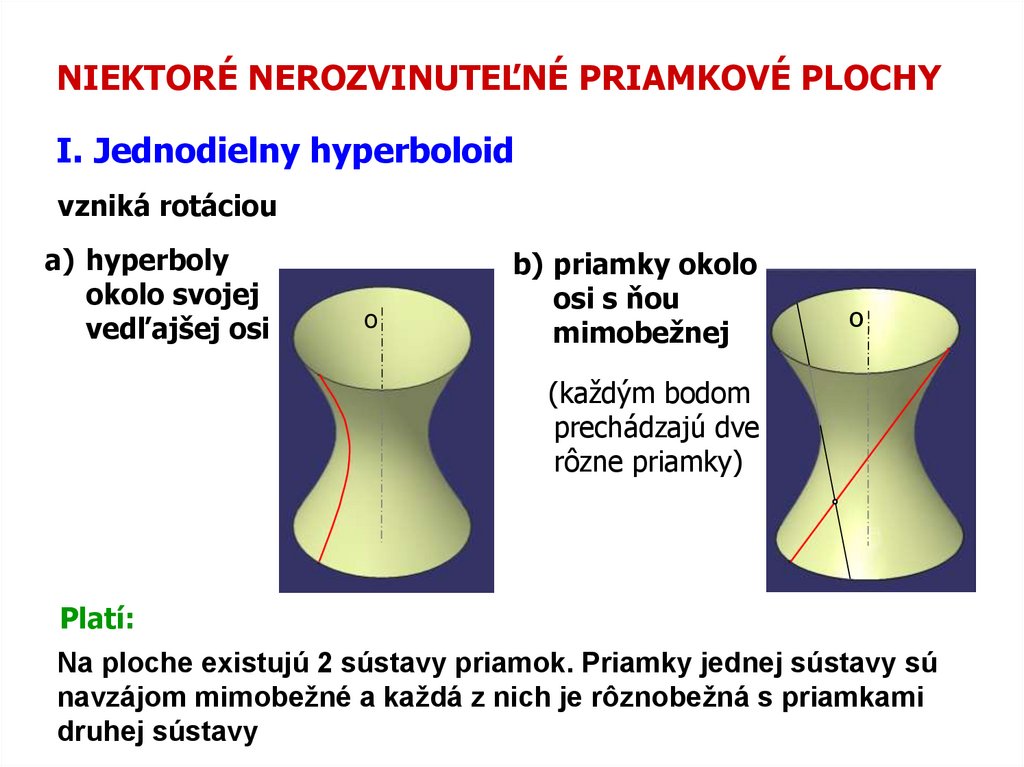
NIEKTORÉ NEROZVINUTEĽNÉ PRIAMKOVÉ PLOCHY
I. Jednodielny hyperboloid
vzniká rotáciou
a) hyperboly
okolo svojej
vedľajšej osi
o
b) priamky okolo
osi s ňou
mimobežnej
o
o
(každým bodom
prechádzajú dve
rôzne priamky)
Platí:
Na ploche existujú 2 sústavy priamok. Priamky jednej sústavy sú
navzájom mimobežné a každá z nich je rôznobežná s priamkami
druhej sústavy

7.

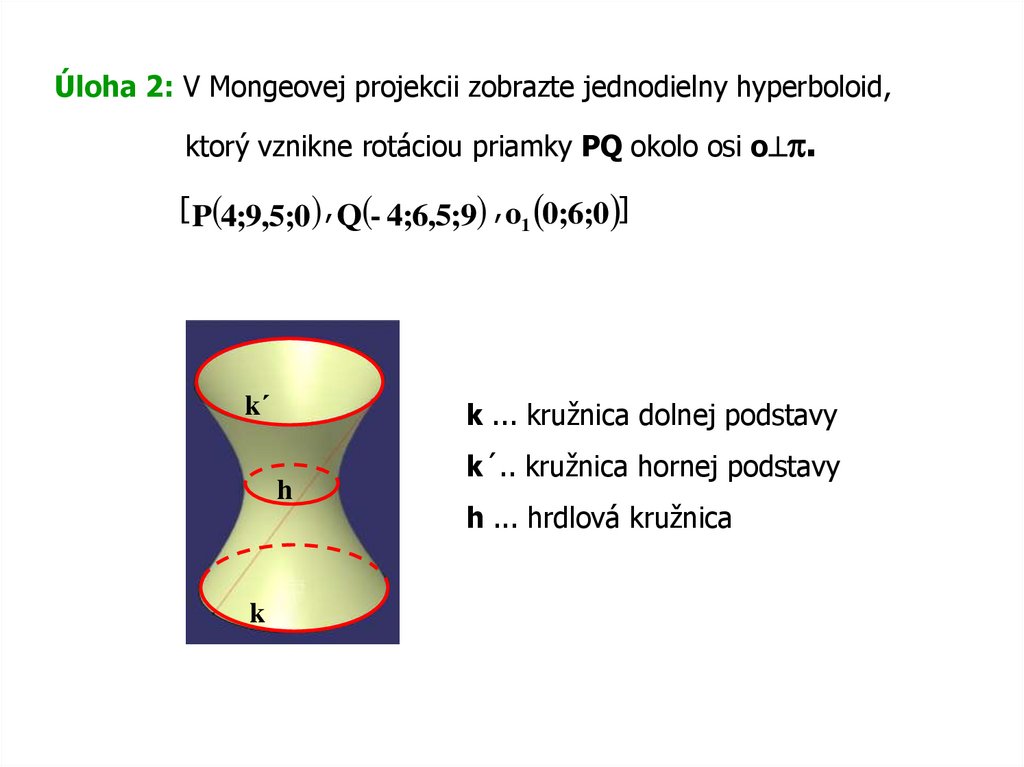
Úloha 2: V Mongeovej projekcii zobrazte jednodielny hyperboloid,
ktorý vznikne rotáciou priamky PQ okolo osi o .
[ P(4;9,5;0) , Q(- 4;6,5;9) , o1 0;6;0 ]
k´
k ... kružnica dolnej podstavy
h
k
k´.. kružnica hornej podstavy
h ... hrdlová kružnica

8.

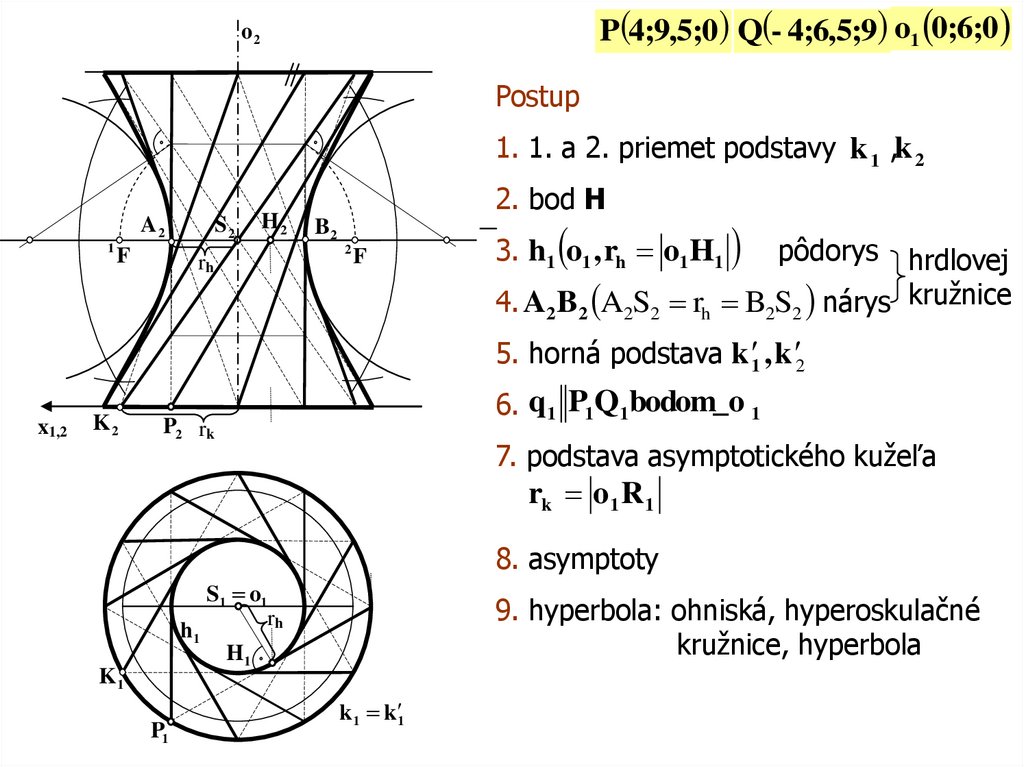
P(4;9,5;0) Q(- 4;6,5;9) o1 0;6;0
o2o2
k 2
Postup
Q2
1. 1. a 2. priemet podstavy k 1 ,k 2
A2
1
1
F
A2
F
rh
S2
rh
S 2 H H2
2
2. bod H
B2
B2
2
2
F
F
3. h1 o1 , rh o1H1
pôdorys
hrdlovej
4. A B A S r B S nárys kružnice
2
2
2 2
h
2 2
5. horná podstava k 1 , k 2
x1,2 K
x1,2
2
P
P2 2rk rrkk
rk
6. q1 P1Q1bodom_o 1
k2
7. podstava asymptotického kužeľa
rk o1 R 1
K1
S o
o
S1 11 o1 1
rh
r
h
h
1
R1 h1 rrkk
k H1
H
r
rkkk1
P
P1 1
q1
Q1
k k
k 1 1 k 1 1
8. asymptoty
9. hyperbola: ohniská, hyperoskulačné
kružnice, hyperbola

9.

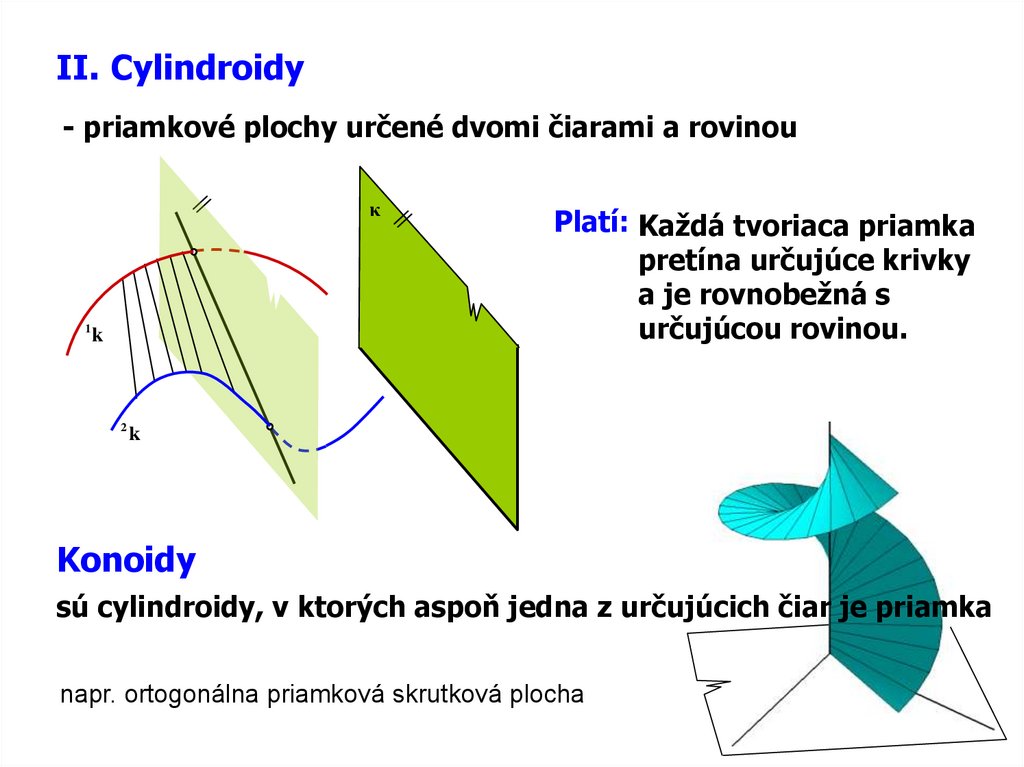
II. Cylindroidy
- priamkové plochy určené dvomi čiarami a rovinou
κ
1
k
2
Platí: Každá tvoriaca priamka
pretína určujúce krivky
a je rovnobežná s
určujúcou rovinou.
k
Konoidy
sú cylindroidy, v ktorých aspoň jedna z určujúcich čiar je priamka
napr. ortogonálna priamková skrutková plocha

10.

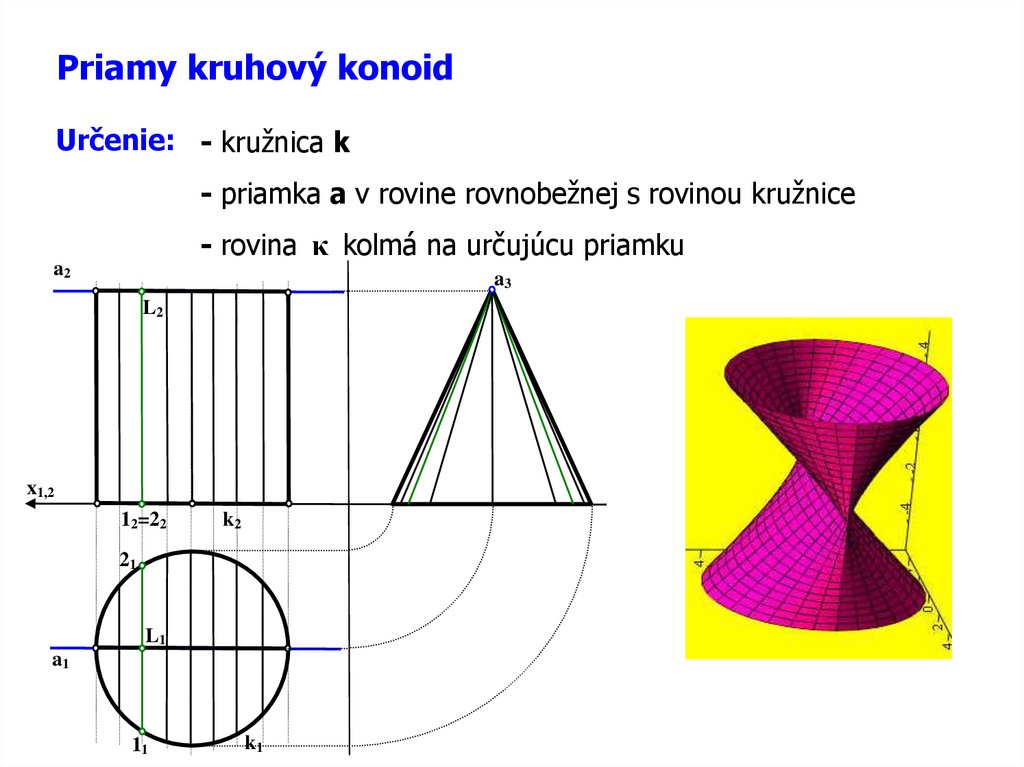
Priamy kruhový konoid
Určenie: - kružnica k
- priamka a v rovine rovnobežnej s rovinou kružnice
- rovina κ kolmá na určujúcu priamku
a2
a3
L2
x1,2
12=22
k2
21
L1
a1
11
k1

11.

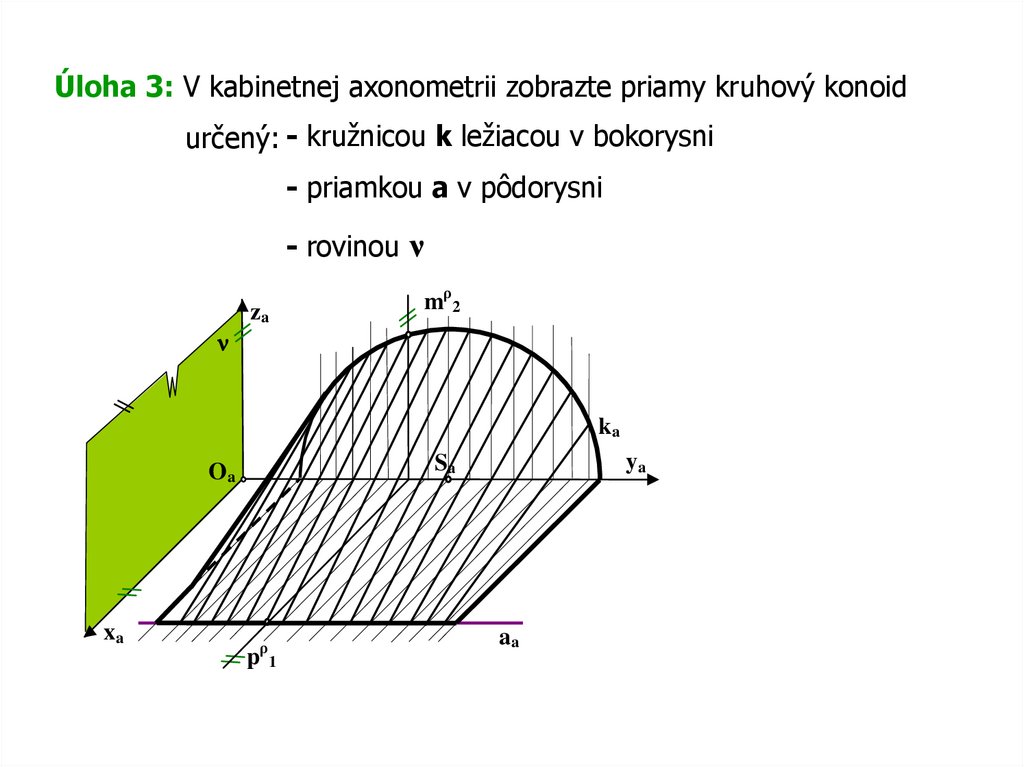
Úloha 3: V kabinetnej axonometrii zobrazte priamy kruhový konoid
určený: - kružnicou k ležiacou v bokorysni
- priamkou a v pôdorysni
- rovinou ν
za
mρ2
´
ya
Sa
Oa
xa
ka
p ρ1
aa

12.

13.

14.

Rekreačný park, Lipno nad Vltavou, ČR

15.

Súdna budova v Bostone, USA

16.

Hyperbolický paraboloid
Určenie: - priamka a
- priamka b
mimobežné
- rovina rôznobežná s priamkami a, b
Vlastnosti:
- na ploche sú 2 sústavy priamok, pričom priamky jednej sústavy sú
navzájom mimobežné a rôznobežné s každou priamkou druhej sústavy
- zachováva sa deliaci pomer priesečníkov tvoriacich priamok jednej sústavy
s tromi rôznymi rovinami rovnobežnými s určujúcou rovinou
Hyperbolický paraboloid je dostatočne určený
priestorovým 4-uholníkom

17.

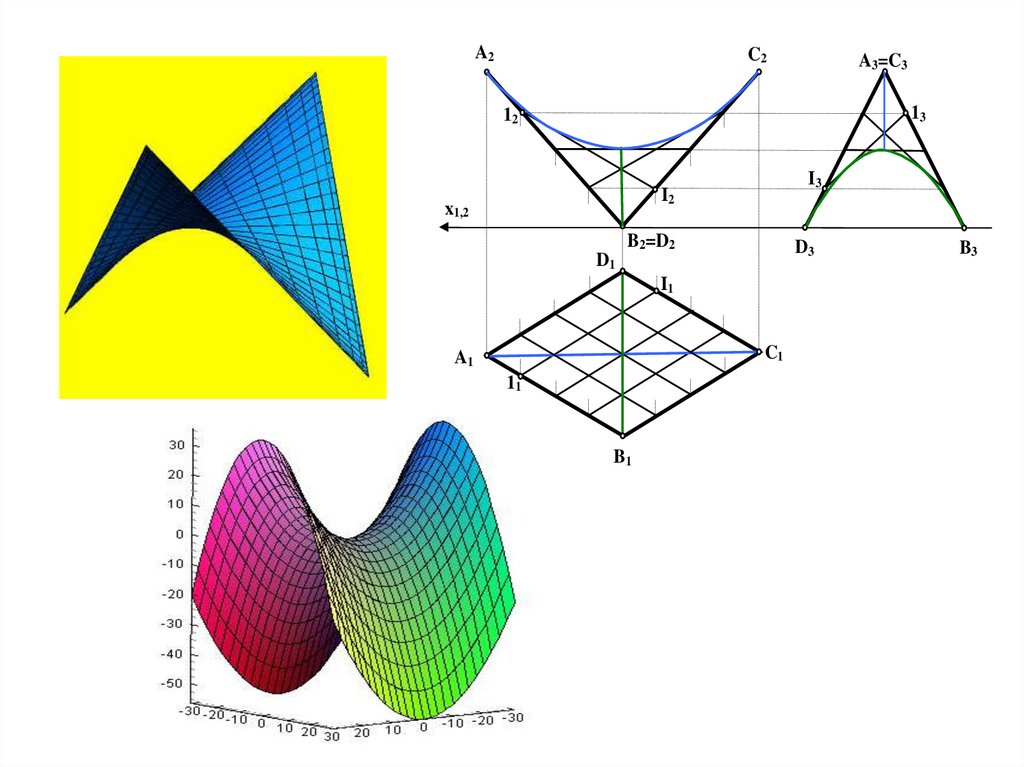
A2
C2
A3=C3
13
12
I3
I2
x1,2
B2=D2
D3
D1
I1
C1
A1
11
B1
B3

18.

19.

Športová hala Pasienky, Bratislava, SR

20.

Športový areál , Connecticut, USA

21.

Benzínová stanica v Markham Moor, GB

22.

Oceánografické múzeum vo Valencii, Španielsko

23.

24.

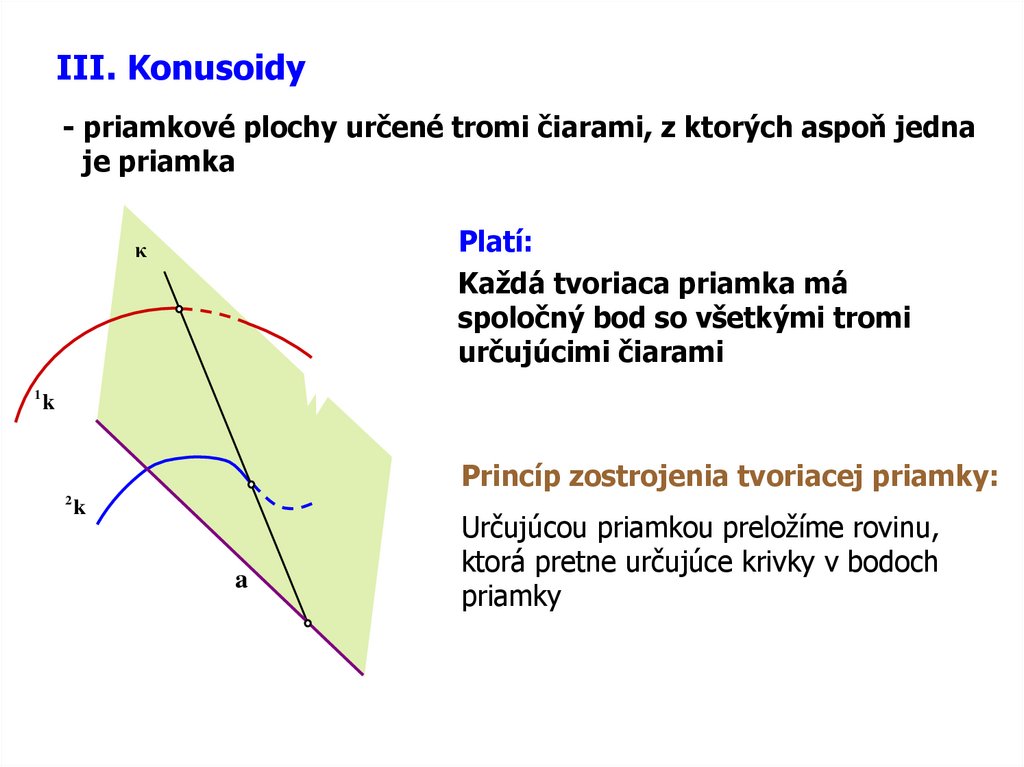
III. Konusoidy
- priamkové plochy určené tromi čiarami, z ktorých aspoň jedna
je priamka
Platí:
Každá tvoriaca priamka má
spoločný bod so všetkými tromi
určujúcimi čiarami
κ
1
k
Princíp zostrojenia tvoriacej priamky:
2
k
a
Určujúcou priamkou preložíme rovinu,
ktorá pretne určujúce krivky v bodoch
priamky

25.

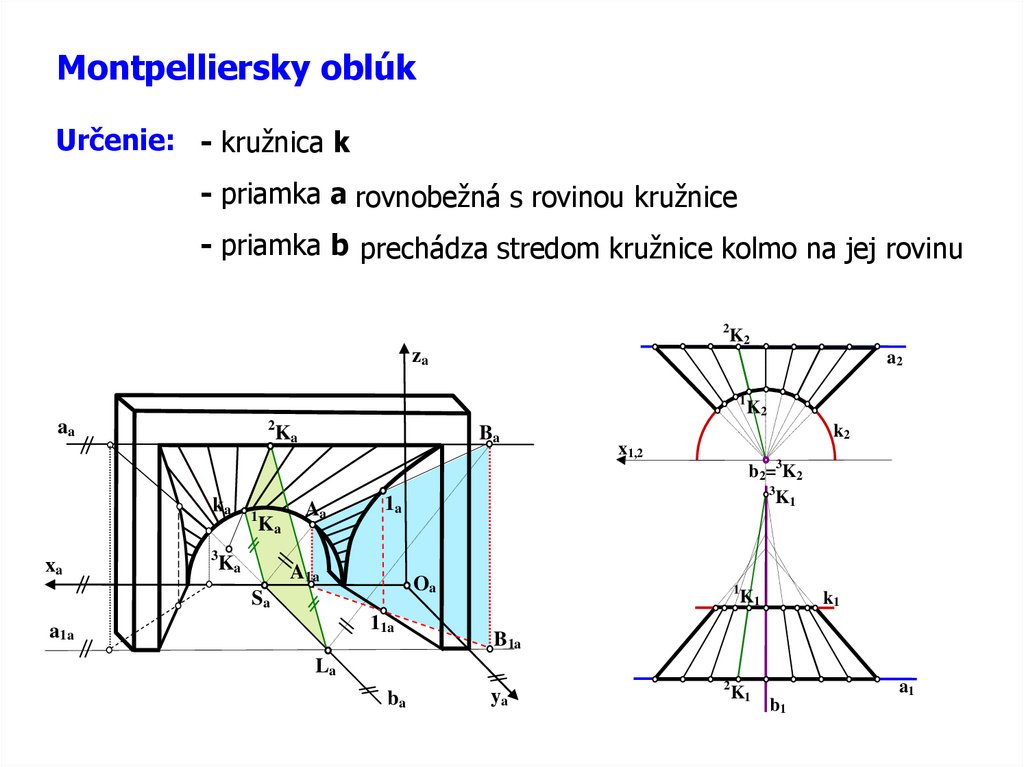
Montpelliersky oblúk
Určenie: - kružnica k
- priamka a rovnobežná s rovinou kružnice
- priamka b prechádza stredom kružnice kolmo na jej rovinu
2
K2
zzaa
a2
1
aa
22
K
Kaa
kkaa
xaa
11
K
Kaa
33
K
Kaa
Ba
Aa
b2=3K2
3
K1
O
Oaa
SSaa
11a
aa1a
1a
k2
x1,2
1a
A1a
K2
1
K1
k1
B1a
LLaa
bbaa
yyaa
2
K1
a1
b1

26.

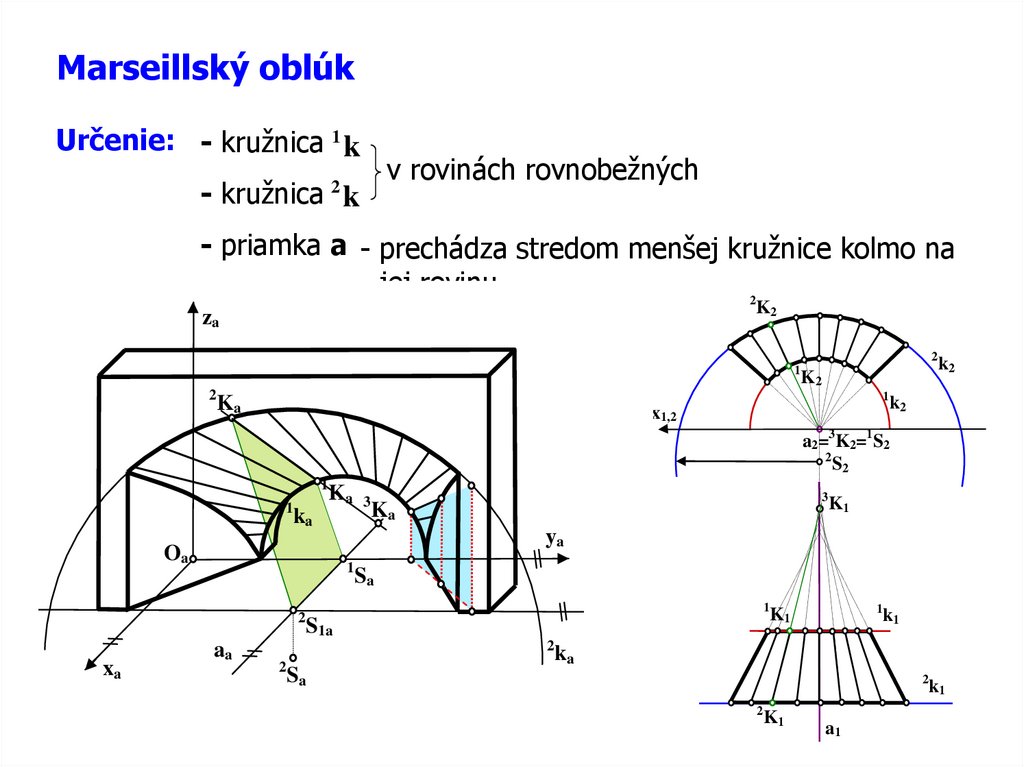
Marseillský oblúk
Určenie: - kružnica 1 k
- kružnica k
2
v rovinách rovnobežných
- priamka a - prechádza stredom menšej kružnice kolmo na
jej rovinu
2
K2
za
2
1
K2
2
1
Ka
x1,2
Oa
k2
a2=31S
K22=1S2
2
S2
1
Ka
1
Ka 3
1
Ka
ka
k2
3
1
ka
K1
ya
1
Sa
1
2
S1a
xa
aa
1
K1
k1
2
2
ka
Sa
2
2
K1
a1
k1

27.

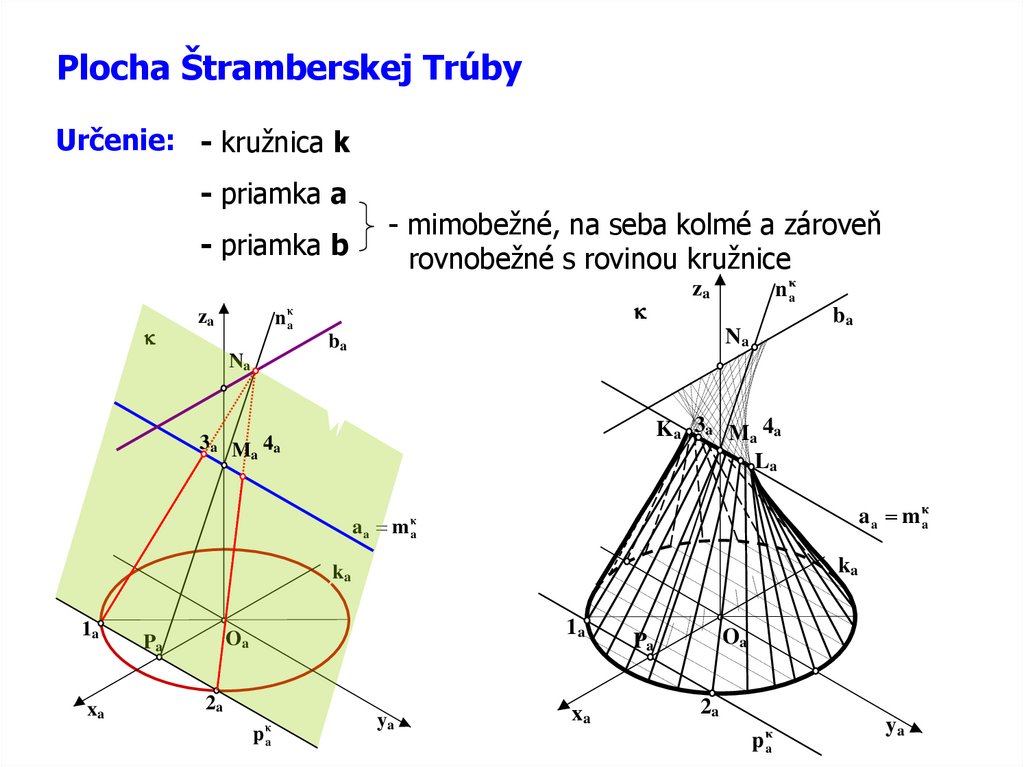
Plocha Štramberskej Trúby
Určenie: - kružnica k
- priamka a
- mimobežné, na seba kolmé a zároveň
rovnobežné s rovinou kružnice
- priamka b
n κa
Oa
za
Na
n κa
Oa
za
Na
ba
Ka 3a Ma 4a
La
3a Ma 4a
a a m κa
Oa
a a m κa
Oa
ka
ka
1a
xa
1a
Oa
Pa
2a
p
κ
a
ba
ya
xa
Oa
Pa
2a
p κa
ya

28.

Štramberská Trúba, ČR

29. Ďakujem za pozornosť