https_ms_edu_tatar_ru_ej_attachments_files_002_178_345_original

1.

2.

Британский математик и священник
Томас
Байес
(1702—1761)
опубликовал при жизни всего две
работы — одну богословскую,
другую математическую.
Тем не менее сегодня без его имени не обходится ни один
учебник по теории вероятностей. В его работе,
опубликованной в 1763 г. уже после смерти автора, был
предложен «метод для корректировки убеждений,
основанный на обновлённых данных».

3.

Формула Байеса или теорема гипотез является
следствием формулы полной вероятности и теоремы
умножения вероятностей. Она дает возможность
пересчитать «априорные» (имевшиеся до проведения
опыта) вероятности гипотез Р(Hn) с учетом результата
проведенного опыта, то есть определять так
называемые
«апостериорные»
(после
опыта)
вероятности P(Hn | A).

4.

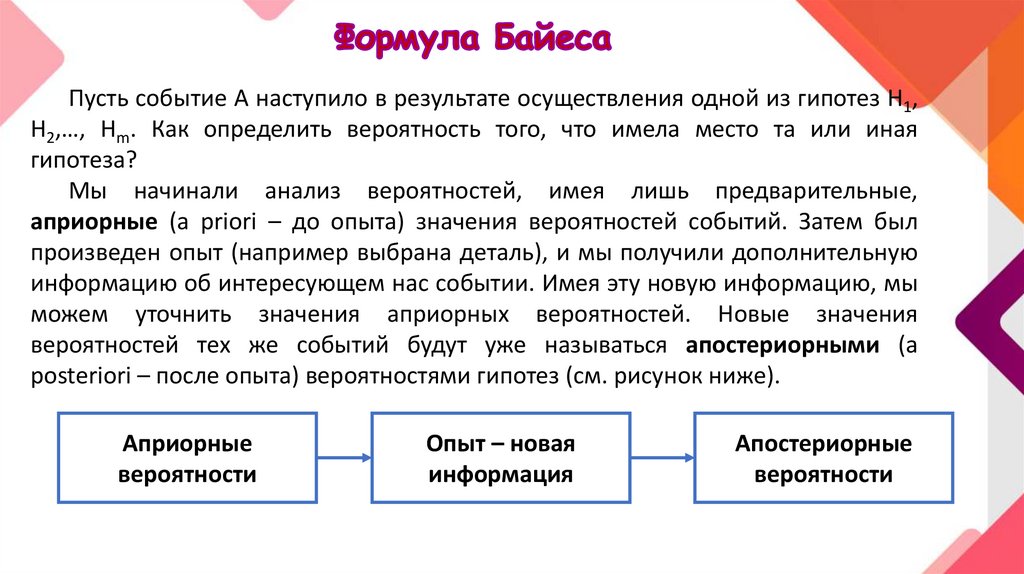
Пусть событие А наступило в результате осуществления одной из гипотез Н1,
Н2,…, Нm. Как определить вероятность того, что имела место та или иная
гипотеза?
Мы начинали анализ вероятностей, имея лишь предварительные,
априорные (a priori – до опыта) значения вероятностей событий. Затем был
произведен опыт (например выбрана деталь), и мы получили дополнительную
информацию об интересующем нас событии. Имея эту новую информацию, мы
можем уточнить значения априорных вероятностей. Новые значения
вероятностей тех же событий будут уже называться апостериорными (a
posteriori – после опыта) вероятностями гипотез (см. рисунок ниже).
Априорные
вероятности
Опыт – новая
информация
Апостериорные
вероятности

5.

Если уже наступило рассматриваемое некоторое
событие A, происходящее с одним из событий